Таким образом, турбулентное течение всегда является неустановившимся, так как значения скоростей и давлений, а также траектории частиц изменяются по времени. Однако его можно рассматривать как установившееся течение при условии, что осредненные по времени значения скоростей и давлений, а также полный расход потока не изменяются со временем. Такое течение на практике считают приближенно стационарным, или квазистационарным.
|
|
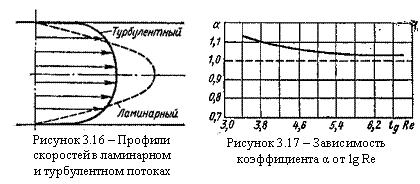
Распределение скоростей (осредненных по времени) в поперечном сечении турбулентного потока существенно отличается от того, которое характерно для ламинарного течения. Если сравним кривые распределения скоростей в ламинарном и турбулентном потоках в одной и той же трубе и при одном и том же расходе (одинаковой средней скорости), то обнаружим существенное различие (рисунок 3.16). Распределение скоростей при турбулентном течении более равномерное,
а нарастание скорости у стенки более крутое, чем при ламинарном течении, для которого характерен параболический закон распределения скоростей.
В связи с этим коэффициент Кориолиса α, учитывающий неравномерность распределения скоростей в уравнении Бернулли при турбулентном течении значительно меньше, нежели при ламинарном.
В отличие от ламинарного течения, где коэффициент Кориолиса α не зависит от числа Re и равен 2, здесь коэффициент α является функцией числа Re и уменьшается с увеличением последнего от 1,13 при
Re = Reкр до 1,025 при Re = 3·106. Как видно из графика, приведенного на рисунке 3.17, кривая α при возрастании числа Re приближается
к единице, поэтому в большинстве случаев при турбулентном течении можно принимать α = 1.
 Так как при турбулентном течении отсутствует слоистость потока и происходит перемешивание жидкости, закон трения Ньютона в этом случае выражает лишь малую часть полного касательного напряжения. Благодаря перемешиванию жидкости и непрерывному переносу количества движения в поперечном направлении касательное напряжение τ0 на стенке трубы в турбулентном потоке значительно больше, чем
Так как при турбулентном течении отсутствует слоистость потока и происходит перемешивание жидкости, закон трения Ньютона в этом случае выражает лишь малую часть полного касательного напряжения. Благодаря перемешиванию жидкости и непрерывному переносу количества движения в поперечном направлении касательное напряжение τ0 на стенке трубы в турбулентном потоке значительно больше, чем
в ламинарном при тех же значениях числа Re и динамического давления ρυ2/2, подсчитанных по средней скорости потока.
В связи с этим потери энергии при турбулентном течении жидкости в трубах также получаются иными, нежели при ламинарном.
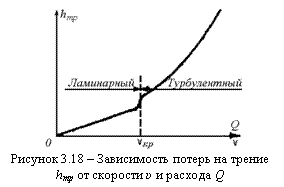
В турбулентном потоке при значениях Re > Reкp потери напора на трение
по длине значительно больше, чем при ламинарном течении при тех же размерах трубы, расходе и вязкости жидкости, а следовательно, при одинаковых числах Re (ламинарный режим при этом неустойчив).
Если при ламинарном течении потеря напора на трение возрастает пропорционально скорости (расходу) в первой степени, то при переходе к турбулентному течению заметны некоторый скачок сопротивления и затем более крутое нарастание величины hтр по кривой, близкой к параболе второй степени (рисунок 3.18).
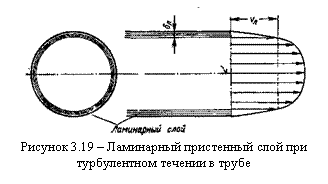 |
Ввиду сложности турбулентного течения и трудностей его аналитического исследования до настоящего времени для него нет достаточно строгой и точной теории. В большинстве случаев для практических расчетов, связанных с турбулентным течением жидкостей в трубах, пользуются экспериментальными данными, систематизированными на основе теории гидродинамического подобия. Большое значение при этом имеет движение жидкости непосредственно на стенке трубы. Здесь имеется тонкий подслой, в котором превалируют силы вязкости, а движение происходит без перемешивания (см. рисунок 3.19). Этот слой называется ламинарным (вязким). В его пределах скорость круто нарастает от нуля на стенке до некоторой конечной величины υл на границе слоя. Толщина δл ламинарного слоя крайне невелика, причем оказывается, что число Re, подсчитанное по толщине δл, скорости υл
и кинематической вязкости ν, есть величина постоянная, то есть
![]() .
.
Эта величина в соответствии с теорией гидродинамического подобия имеет универсальное постоянное значение подобно тому, как постоянно число Reкp для течения в трубах. Поэтому при увеличении скорости потока и, следовательно, числа Re растет также скорость υл ,
а толщина δл ламинарного слоя уменьшается.
Основной расчетной формулой для потерь напора при турбулентном течении в круглых трубах является уже приводившаяся выше эмпирическая формула, называемая формулой Вейсбаха-Дарси и имеющая следующий вид:
![]() , (3.29)
, (3.29)
где λт – коэффициент потерь на трение при турбулентном течении, или коэффициент Дарси.
Эта основная формула применима как при турбулентном, так и при ламинарном течении, различие заключается лишь в значениях коэффициента λ.
3.9.2 Определение коэффициента потерь на трение. Никурадзе
Для определения коэффициента потерь на трение λ при турбулентном режиме предложен ряд эмпирических и полуэмпирических формул, полученных многими авторами в результате исследования различных областей гидравлического трения. Однако фундаментальным исследованием стала работа , который в 1933 г. опубликовал результаты своих многочисленных опытов, представленных в виде особого графика.
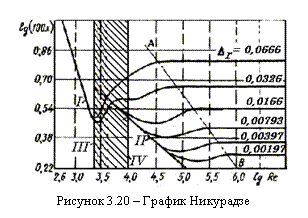 |
В своих опытах Никурадзе исследовал напорное движение жидкости в круглоцилиндрических трубах, имеющих однозернистую равномерно распределенную (равнозернистую) шероховатость, которую он создавал путем наклеивания калиброванных песчинок высотой Δ на внутреннюю поверхность трубы.
Полученный Никурадзе график представляет собой семейство кривых, построенных в логарифмических координатах (по горизонтальной оси отложены величины lg ReD, а по вертикальной – lg 100λ) по точкам, соответствующим опытам с трубами с различной относительной шероховатостью Δr = Δ : D, от Δr = 0,00197 до
Δr = 0,0666.
Рассмотрим подробно график Никурадзе (рисунок 3.20). Все поле графика можно условно разбить на пять областей.
Первая область – область ламинарного режима при Re < 2300, (lg Re ≤ 3,36); здесь все опытные точки независимо от шероховатости уложились на одну прямую линию I, уравнение которой λ = 64 / Re.
Вторая область, расположенная между вертикалями III и IV, – область неустойчивого режима, или переходная (числа Рейнольдса лежат в пределах от 2300 до 10000). Здесь возможно существование как ламинарного, так и турбулентного режимов, экспериментальные точки имеют значительный разброс.
Третья область – область «гидравлически гладких труб» при турбулентном режиме; здесь толщина вязкого подслоя существенно больше высоты выступов шероховатости, и турбулентное ядро потока не соприкасается с ними. Поэтому в данной области коэффициент
λ = f (Re) не зависит от шероховатости. Область гладких труб представлена на графике прямой линией II, уравнение которой
![]() . (3.30)
. (3.30)
Эта эмпирическая формула была получена Блазиусом в 1913г.
в результате обработки многочисленных опытов по исследованию движения жидкости в круглых гладких латунных трубах при числах Рейнольдса Re от 2300 до 100000.
Четвертая область – область турбулентного режима доквадратичного сопротивления шероховатых труб, лежит между прямой II
и линией АВ, образованной точками, отделяющими горизонтальные участки кривых с некоторой заданной точностью. Можно видеть, что
в этой области каждая кривая отвечает определенному значению относительной шероховатости. Здесь турбулентное ядро постепенно раскрывает шероховатость, поэтому имеет место наиболее общий случай λ = f (Re, Δr).
Пятая область – область турбулентного режима квадратичного сопротивления шероховатых труб, располагается правее и выше линий АВ. Здесь коэффициент λ не зависит от числа Рейнольдса Re (все линии графика – прямые, параллельные горизонтальной оси). Коэффициент λ, а следовательно, и потеря напора hтр зависят от шероховатости
λ = f (Δr). Таким образом, как видно из формулы Вейсбаха-Дарси,
для этой области сопротивления потеря напора по длине прямо пропорциональна квадрату средней скорости.
В заключение необходимо отметить, что общий качественный характер зависимостей коэффициента гидравлического трения λ, полученный Никурадзе для труб круглого сечения, распространяется и на другие потоки, в том числе и безнапорные, что было подтверждено опытами , в которых исследовалось безнапорное движение жидкости в лотке прямоугольного сечения, имеющего различную равнозернистую шероховатость. Важно также подчеркнуть, что после указанных работ отпала необходимость создавать особые расчетные зависимости для различных жидкостей, так как род жидкости учитывается числом Рейнольдса.
3.9.3 Практические способы определения коэффициента
гидравлического трения λ для напорных технических труб
Трубы, находящиеся в эксплуатации, подвергаются коррозии
и покрываются различными отложениями, имеют разнозернистую шероховатость; выступы шероховатости различной формы и размеров, расстояние между ними неодинаковое (см. рисунок 3.20).
Опыты, проведенные рядом авторов с техническими трубами, показали, что характер зависимости коэффициента λ от числа Рейнольдса отличается от результатов, полученных Никурадзе, особенно в области доквадратичного сопротивления. Здесь в отличие от графика Никурадзе кривые Δr = const, опускаясь вниз, постепенно переходят от вида, соответствующего области гладкого сопротивления (где согласно формуле Блазиуса ![]() ), к виду, отвечающему области квадратичного сопротивления. Таким образом, в области доквадратичного сопротивления потеря напора по длине пропорциональна средней скорости υ в степени 1,75 < т < 2,0. Такой постепенный переход объясняют тем, что в случае разнозернистой шероховатости при увеличении числа Рейнольдса, а следовательно, уменьшении толщины вязкого подслоя δ выступы шероховатости вступают в соприкосновение с турбулентным потоком не все одновременно, а сначала наиболее высокие, затем средние и только при числах Re, соответствующих квадратичной области сопротивления, вязкий подслой «раскрывает» все выступы шероховатости.
), к виду, отвечающему области квадратичного сопротивления. Таким образом, в области доквадратичного сопротивления потеря напора по длине пропорциональна средней скорости υ в степени 1,75 < т < 2,0. Такой постепенный переход объясняют тем, что в случае разнозернистой шероховатости при увеличении числа Рейнольдса, а следовательно, уменьшении толщины вязкого подслоя δ выступы шероховатости вступают в соприкосновение с турбулентным потоком не все одновременно, а сначала наиболее высокие, затем средние и только при числах Re, соответствующих квадратичной области сопротивления, вязкий подслой «раскрывает» все выступы шероховатости.
Имея в виду разнозернистую шероховатость, в расчетные зависимости для технических труб вводят некоторую среднюю высоту выступов, именуемую эквивалентной шероховатостью, которую обозначают ![]() .
.
При турбулентном режиме для определения коэффициента λ
в случае движения жидкости в напорных технических трубах используются или экспериментальные графики, или эмпирические
и полуэмпирические формулы. Эти формулы обычно рекомендуются для одной из соответствующих областей сопротивления, приведенных в 3.9.2. Следовательно, прежде чем обращаться к той или иной формуле, необходимо установить область сопротивления, граничными условиями существования которой являются так называемые нижнее ![]() и верхнее
и верхнее ![]() предельные числа Рейнольдса.
предельные числа Рейнольдса.
Согласно эти числа могут быть определены по приближенным формулам:
![]() ,
, 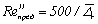 ,
,
где 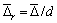 .
.
В случае 10000 < Re < ![]() , где Re – число Рейнольдса, соответствующее рассматриваемому потоку, получаем практически область гладких труб, для которой обычно рекомендуются либо формула Л. Прандтля
, где Re – число Рейнольдса, соответствующее рассматриваемому потоку, получаем практически область гладких труб, для которой обычно рекомендуются либо формула Л. Прандтля
![]() , (3.31)
, (3.31)
или более удобная формула Блазиуса
![]() ,
,
справедливая при числах Рейнольдса Re <
Область доквадратичного сопротивления отвечает числам Рейнольдса, лежащим в пределах
![]() < Re <
< Re < ![]() .
.
Для определения коэффициента λ в этой области сопротивления рекомендуется обобщенная формула Кольбрука, которую он предложил в 1938 г., основываясь на своих опытах с учетом исследований других авторов
![]() , (3.32)
, (3.32)
или более удобная для вычислений формула
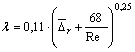 . (3.33)
. (3.33)
В случае Re ≥ ![]() имеем квадратичную область сопротивления, для которой формула (3.32) упрощается и приобретает вид формулы Л. Прандтля для шероховатых труб
имеем квадратичную область сопротивления, для которой формула (3.32) упрощается и приобретает вид формулы Л. Прандтля для шероховатых труб
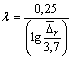 , (3.34)
, (3.34)
а формула приводится к формуле Шифринсона ![]() .
.
Величину средней высоты выступов шероховатости ![]() , которая входит в расчетные формулы, установить непосредственным измерением практически невозможно, так как на распределение скоростей по сечению и касательные напряжения влияет не только высота выступов, но и их форма, а также их шаг расположения на стенке. Поэтому значение
, которая входит в расчетные формулы, установить непосредственным измерением практически невозможно, так как на распределение скоростей по сечению и касательные напряжения влияет не только высота выступов, но и их форма, а также их шаг расположения на стенке. Поэтому значение ![]() для данной трубы находят экспериментально следующим образом. Рассматривая квадратичную область сопротивления опытным путем, пользуясь формулой Вейсбаха-Дарси (3.29), определяют для данной трубы величину λ. Затем по формулам (3.33) или (3.34) вычисляют искомое значение
для данной трубы находят экспериментально следующим образом. Рассматривая квадратичную область сопротивления опытным путем, пользуясь формулой Вейсбаха-Дарси (3.29), определяют для данной трубы величину λ. Затем по формулам (3.33) или (3.34) вычисляют искомое значение ![]() . Найденную таким образом величину
. Найденную таким образом величину ![]() называют эквивалентной шероховатостью, численные значения которой для разных труб приводятся в справочных таблицах [8].
называют эквивалентной шероховатостью, численные значения которой для разных труб приводятся в справочных таблицах [8].
3.10 Местные гидравлические сопротивления
Местными гидравлическими сопротивлениями называются участки трубопроводов (каналов), на которых поток жидкости претерпевает деформацию вследствие изменения размеров или формы сечения, либо направления движения. Простейшие местные сопротивления можно условно разделить на расширения, сужения, которые могут быть плавными и внезапными, и повороты, которые также могут быть плавными и внезапными. Но большинство местных сопротивлений являются комбинациями указанных случаев, так как поворот потока может привести к изменению его сечения, а расширение (сужение) потока – к отклонению от прямолинейного движения жидкости (см. рисунок 3.21б). Кроме того, различная гидравлическая арматура (краны, вентили, клапаны и т. д.) практически всегда является комбинацией простейших местных сопротивлений. К местным сопротивлениям также относят участки трубопроводов с разделением или слиянием потоков жидкости.
Необходимо иметь в виду, что местные гидравлические сопротивления оказывают существенное влияние на работу гидросистем
с турбулентными потоками жидкости. В гидросистемах с ламинарными потоками в большинстве случаев эти потери напора малы по сравнению с потерями на трение в трубах. В данном разделе будут рассмотрены местные гидравлические сопротивления при турбулентном режиме течения.
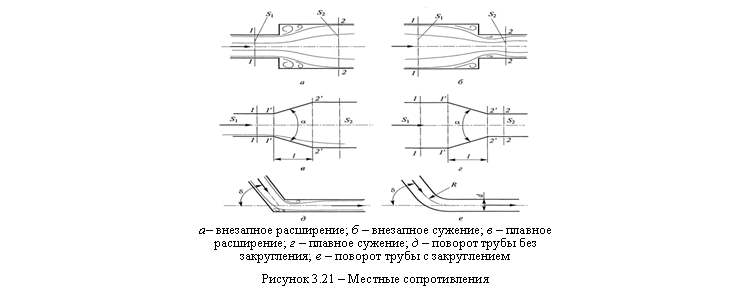 Потери напора в местных гидравлических сопротивлениях называются местными потерями. Несмотря на многообразие местных сопротивлений, в большинстве из них потери напора обусловлены следующими причинами:
Потери напора в местных гидравлических сопротивлениях называются местными потерями. Несмотря на многообразие местных сопротивлений, в большинстве из них потери напора обусловлены следующими причинами:
- искривлением линий тока;
- изменением величины скорости вследствие уменьшения или увеличения живых сечений;
- отрывом транзитных струй от поверхности, вихреобразованием.
Несмотря на многообразие местных сопротивлений, в большинстве из них изменение скоростей движения приводит к возникновению вихрей, которые для своего вращения используют энергию потока жидкости (см. рисунок 3.21б). Таким образом, основной причиной гидравлических потерь напора в большинстве местных сопротивлений является вихреобразование. Практика показывает, что эти потери пропорциональны квадрату скорости жидкости, и для их определения используется формула Вейсбаха
![]() .
.
При вычислении потерь напора по формуле Вейсбаха наибольшей трудностью является определение безразмерного коэффициента местного сопротивления ![]() . Из-за сложности процессов, происходящих в местных гидравлических сопротивлениях, теоретически найти
. Из-за сложности процессов, происходящих в местных гидравлических сопротивлениях, теоретически найти ![]() удается только в отдельных случаях, поэтому большинство значений этого коэффициента получено в результате экспериментальных исследований. Рассмотрим способы определения коэффициента
удается только в отдельных случаях, поэтому большинство значений этого коэффициента получено в результате экспериментальных исследований. Рассмотрим способы определения коэффициента ![]() для наиболее распространенных местных сопротивлений при турбулентном режиме течения.
для наиболее распространенных местных сопротивлений при турбулентном режиме течения.
Для внезапного расширения потока (см. рисунок 3.21б) имеется теоретически полученная формула Борда для коэффициента ![]() , который однозначно определяется соотношением площадей до расширения (S1) и после него (S2):
, который однозначно определяется соотношением площадей до расширения (S1) и после него (S2):
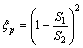 . (3.35)
. (3.35)
Следует отметить частный случай, когда жидкость вытекает из трубы в бак, т. е. когда площадь сечения потока в трубе S1 значительно меньше таковой в баке S2. Тогда из формулы (3.35) следует, что для выхода трубы в бак ![]() = 1. Для оценки коэффициента потерь напора при внезапном сужении
= 1. Для оценки коэффициента потерь напора при внезапном сужении ![]() используется эмпирическая формула, предложенная [8], которая также учитывает соотношение площадей до расширения (S1) и после него (S2):
используется эмпирическая формула, предложенная [8], которая также учитывает соотношение площадей до расширения (S1) и после него (S2):
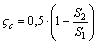 . (3.36)
. (3.36)
Для внезапного сужения потока тоже необходимо отметить частный случай, когда жидкость вытекает из бака по трубе, т. е. когда площадь сечения потока в трубе S2 значительно меньше таковой в баке S1. Тогда из (3.36) следует, что для входа трубы в бак ![]() = 0,5.
= 0,5.
В гидравлических системах достаточно часто встречаются плавное расширение потока (рисунок 3.21в) и плавное сужение потока (рисунок 3.21г). Расширяющееся русло в гидравлике принято называть диффузором, а сужающееся – конфузором. При этом если конфузор выполнен с плавными переходами в сечениях 1'–1' и 2'–2', то его
называют соплом. Эти местные гидравлические сопротивления могут иметь (особенно при малых углах α) достаточно большую длину l. Поэтому кроме потерь из-за вихреобразования, вызванного изменением геометрии потока, в этих местных сопротивлениях учитывают потери напора на трение по длине.
Значения коэффициентов для плавного расширения ![]() и плавного сужения
и плавного сужения ![]() находят путем введения поправочных коэффициентов в формулы (3.35) и (3.36):
находят путем введения поправочных коэффициентов в формулы (3.35) и (3.36): ![]() и
и ![]() .
.
Поправочные коэффициенты kp и kc имеют численные значения меньше единицы, зависят от углов α, а также от плавности переходов в сечениях 1'–1' и 2'–2'. Их значения приводятся в справочниках.
Весьма распространенными местными сопротивлениями являются также повороты потоков. Они могут быть с внезапным поворотом трубы (рисунок 3.21д) или с плавным поворотом (рисунок 3.21е).
Внезапный поворот трубы (или колено) вызывает значительные вихреобразования и поэтому приводит к существенным потерям напора. Коэффициент сопротивления колена ![]() определяется, в первую очередь, углом поворота δ и может быть выбран из справочника.
определяется, в первую очередь, углом поворота δ и может быть выбран из справочника.
Плавный поворот трубы (или отвод) существенно снижает вихреобразование и, следовательно, потери напора. Коэффициент ![]() для данного сопротивления зависит не только от угла поворота δ, но и от относительного радиуса поворота R/d. Для определения коэффициента
для данного сопротивления зависит не только от угла поворота δ, но и от относительного радиуса поворота R/d. Для определения коэффициента ![]() существуют различные эмпирические зависимости, например,
существуют различные эмпирические зависимости, например,
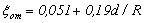 , (3.37)
, (3.37)
либо его значения находятся в справочной литературе.
Коэффициенты потерь других местных сопротивлений, встречающихся в гидравлических системах, также могут быть определены по справочнику.
Следует иметь в виду, что два или более гидравлических сопротивления, установленных в одной трубе, могут оказывать взаимное влияние, если расстояние между ними менее 40d (d – диаметр трубы).
3.11 Местные сопротивления при больших и малых числах Рейнольдса. Метод эквивалентной длины
Ранее были рассмотрены местные гидравлические сопротивления, потери напора в которых пропорциональны квадрату скорости или
расхода. Однако квадратичный характер зависимости потерь – наиболее распространенный, но все же частный случай для местного сопротивления.
 В машиностроительных гидросистемах встречаются местные сопротивления, внутри которых имеет место ламинарное течение. Потери напора в таких сопротивлениях пропорциональны скорости (или расходу) в первой степени, т. е. носят линейный характер. Кроме того, при ламинарном течении жидкости в трубах коэффициенты местных сопротивлений не всегда остаются постоянными. Указанные сопротивления встречаются существенно реже, чем сопротивления с квадратичной зависимостью потерь, и не имеют определяющего значения, но при расчете отдельных гидросистем их необходимо учитывать.
В машиностроительных гидросистемах встречаются местные сопротивления, внутри которых имеет место ламинарное течение. Потери напора в таких сопротивлениях пропорциональны скорости (или расходу) в первой степени, т. е. носят линейный характер. Кроме того, при ламинарном течении жидкости в трубах коэффициенты местных сопротивлений не всегда остаются постоянными. Указанные сопротивления встречаются существенно реже, чем сопротивления с квадратичной зависимостью потерь, и не имеют определяющего значения, но при расчете отдельных гидросистем их необходимо учитывать.
В качестве примера рассмотрим жиклер (рисунок 3.22), в канале которого существует ламинарное течение. Потери напора в жиклере будут складываться из потерь на трение в канале и потерь на внезапное расширение потока при выходе из этого канала. Причем первый вид из указанных потерь будет пропорционален скорости в первой степени (так как в канале ламинарное течение), а второй – квадрату скорости (потери на вихреобразование).
Если принимать во внимание оба вида потерь, то формула для коэффициента сопротивления жиклера будет иметь вид
![]() . (3.38)
. (3.38)
Это общее выражение для коэффициента любого местного сопротивления. Первое слагаемое в (3.38) учитывает линейные потери,
а второе – квадратичные. Соотношение между первым и вторым слагаемыми зависит от геометрических размеров каждого конкретного сопротивления.
Использование зависимости (3.38) приводит к значительному усложнению при расчетах гидравлических систем. Однако практика показывает, что в подавляющем большинстве местных сопротивлений один из видов потерь существенно превышает второй, поэтому при проведении реальных расчетов одним из слагаемых формулы (3.38) пренебрегают.
На практике для местных сопротивлений с линейным законом сопротивления (или с законом, близким к линейному) часто применяют метод эквивалентной длины. Сущность этого метода заключается
в том, что для местного сопротивления задаются эквивалентная длина и условный диаметр (или условная площадь сечения). Причем их значения выбираются такими, что потери напора в условном трубопроводе равны потерям в данном гидравлическом сопротивлении. Тогда потери в трубопроводе с таким местным сопротивлением можно рассчитать по обобщенной формуле Пуазейля
![]() ,
,
где lp = l +lэкв – расчетная длина трубопровода, м;
l – фактическая длина, м;
lэкв – эквивалентная длина, м.
К таким сопротивлениям относятся большинство фильтров,
а также линейные дроссели и некоторые жиклеры.
4 ИСТЕЧЕНИЕ ЖИДКОСТИ
ЧЕРЕЗ ОТВЕРСТИЯ И НАСАДКИ
4.1 Истечение через отверстие в тонкой стенке
Рассмотрим истечение жидкости через отверстие диаметром d0
в стенке бака, расположенное на глубине Н0, в газовую среду с некоторым давлением р1 (рисунок 4.1a). При этом предполагается, что если отверстие мало по сравнению с размерами бака и глубиной Н0, то
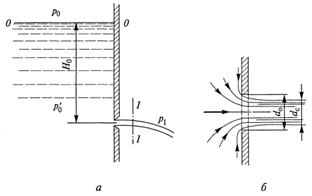
Рисунок 4.1 – Схемы истечения жидкости через отверстие в тонкой стенке в газовую среду (а) и формирование струи (б)
другие стенки бака и свободная поверхность жидкости не влияют на приток жидкости к отверстию.
Характер истечения в этом случае показан на рисунке 4.1б. Частицы жидкости приближаются к отверстию из всего близлежащего объема, двигаясь по различным траекториям. Некоторые из них при попадании в отверстие должны изменить направление своего движения на 90°. Так как каждая частица имеет массу, то мгновенно изменить направление своего движения она не может. Следствием этого является сжатие струи жидкости при истечении. Процесс сжатия струи практически завершается на расстоянии, равном примерно одному диаметру отверстия, и после этого струя приобретает цилиндрическую форму с диаметром поперечного сечения dc. Точно такими же будут условия истечения, если отверстие выполнено в толстой стенке со снятием фаски с внешней стороны.
Степень сжатия струи оценивается коэффициентом сжатия ε, равным отношению площади поперечного сечения струи к площади отверстия
![]() . (4.1)
. (4.1)
Определим расход Q жидкости через рассматриваемое отверстие. Для этого запишем уравнение Бернулли для двух сечений (см. рисунок 4.1а): сечения 0–0 и сечения 1–1. Сечение 0–0 – это открытая поверхность жидкости в баке, следовательно, в нем давление р0, а скорость жидкости можно считать равной нулю. Сечение 1–1 струи должно быть выбрано в той ее части, где струя уже приняла цилиндрическую форму; тогда в этом сечении давление равно давлению р1 окружающей среды. Если в качестве плоскости сравнения выбрать горизонтальную плоскость, проходящую через ось отверстия, то получим
![]() ,
,
где α – коэффициент Кориолиса, учитывающий неравномерность распределения скорости по сечению 1–1 струи;
![]() – средняя скорость жидкости в сечении 1–1, м;
– средняя скорость жидкости в сечении 1–1, м;
![]() – коэффициент сопротивления отверстия, учитывающий торможение частиц жидкости о входную кромку отверстия.
– коэффициент сопротивления отверстия, учитывающий торможение частиц жидкости о входную кромку отверстия.
Перенесем первое слагаемое правой части уравнения в левую часть и обозначим ее как расчетный напор 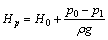 ,
,
тогда 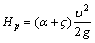 ;
;
отсюда средняя скорость истечения жидкости
![]() , (4.2)
, (4.2)
где ![]() – безразмерная величина, получившая название коэффициент скорости и определяемая по формуле
– безразмерная величина, получившая название коэффициент скорости и определяемая по формуле
![]() . (4.3)
. (4.3)
В случае истечения идеальной жидкости (α = 1 и ![]() = 0) из формулы (4.3) следует, что
= 0) из формулы (4.3) следует, что ![]() = 1, т. е. скорость истечения идеальной жидкости
= 1, т. е. скорость истечения идеальной жидкости
![]() . (4.4)
. (4.4)
Таким образом, на основании сравнения формул (4.3) и (4.4) можно сформулировать физический смысл коэффициента скорости ![]() . Это величина, равная отношению средней скорости истечения реальной жидкости к скорости истечения идеальной жидкости в тех же условиях. Очевидно, что при истечении реальной жидкости коэффициент
. Это величина, равная отношению средней скорости истечения реальной жидкости к скорости истечения идеальной жидкости в тех же условиях. Очевидно, что при истечении реальной жидкости коэффициент ![]() всегда меньше единицы.
всегда меньше единицы.
Расход Q при истечении определим как произведение средней скорости истечения реальной жидкости и фактической площади живого сечения струи. Используя формулы (4.1) и (4.3), получим
![]() .
.
Произведение двух безразмерных коэффициентов ![]() и
и ![]() принято называть коэффициентом расхода и обозначать
принято называть коэффициентом расхода и обозначать
![]() . (4.5)
. (4.5)
Тогда
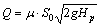 . (4.6)
. (4.6)
Из (4.6) следует, что
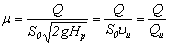 .
.
Таким образом, физический смысл коэффициента расхода ![]() состоит в том, что он численно равен отношению действительного расхода Q при истечении жидкости к тому расходу Qu, который имел бы место при отсутствии сжатия струи и сопротивления истечению.
состоит в том, что он численно равен отношению действительного расхода Q при истечении жидкости к тому расходу Qu, который имел бы место при отсутствии сжатия струи и сопротивления истечению.
Следует обратить внимание на то, что Qu не является расходом при истечении идеальной жидкости, так как идеальная жидкость отличается от реальной только отсутствием вязкости. Эффект же сжатия струи при истечении идеальной жидкости, связанный с инерционными свойствами частиц жидкости, в условиях отсутствия трения проявляется в еще большей степени.
На практике формула (4.6) используется достаточно редко из-за сложностей, возникающих при определении расчетного напора Hр, особенно в закрытых гидросистемах. Поэтому сделаем следующие преобразования. Обозначим внутри бака на уровне оси отверстия на некотором удалении от него (где скорость жидкости можно принять равной нулю) давление ![]() (см. рисунок 4.1а), тогда перепад давления Δр, под действием которого происходит истечение жидкости через отверстие, запишется в виде
(см. рисунок 4.1а), тогда перепад давления Δр, под действием которого происходит истечение жидкости через отверстие, запишется в виде
![]() .
.
Выразив из этой формулы напор Hp и подставив его в формулу (4.6), получим
![]() . (4.7)
. (4.7)
При помощи формулы (4.7) решается основная задача – определение расхода жидкости при истечении. Она широко применяется при расчетах элементов машиностроительных гидросистем.
Таким образом, нами введены в рассмотрение три коэффициента – ![]() ,
, ![]() и
и ![]() , характеризующие процесс истечения жидкости. Все они являются функцией числа Рейнольдса Re. Однако для маловязких жидкостей (воды, бензина и др.), истечение которых, как правило, происходит при больших значениях числа Re, эти коэффициенты практически постоянны:
, характеризующие процесс истечения жидкости. Все они являются функцией числа Рейнольдса Re. Однако для маловязких жидкостей (воды, бензина и др.), истечение которых, как правило, происходит при больших значениях числа Re, эти коэффициенты практически постоянны: ![]() = 0,64;
= 0,64; ![]() = 0,97;
= 0,97; ![]() = 0,62 [1,3]. При истечении минеральных масел через круглые отверстия в области квадратичного сопротивления можно принять
= 0,62 [1,3]. При истечении минеральных масел через круглые отверстия в области квадратичного сопротивления можно принять ![]() = 0,65.
= 0,65.

|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 |