Гидравлические сопротивления

Гидравлические сопротивления.

Режимы движения жидкости. Опыты Рейнольдса. Число Рейнольдса. Ламинарный режим течения в трубах. Потери напора при ламинарном течении. Турбулентный режим течения. Шероховатость стенок. Гидравлическое сопротивление, коэффициент гидравлического сопротивления l, формулы для его определения. Гидравлические потери при турбулентном режиме. Местные сопротивления, коэффициент местных сопротивлений. Потери напора при течении жидкости в трубах. Сопротивление при обтекании тел.

Режимы движения жидкости

При проведении гидравлического расчёта в первую очередь нужно выяснять: какой режим движения будет наблюдаться у данного потока?

Режимы движения всех потоков (напорных и безнапорных) де­лятся на два типа (рис. 12):

1) ламинарный, то есть спокойный, параллельноструйный, при ма­лых скоростях;

2) турбулентный, то есть бурлящий, вихреобразный, с водоворота­ми, при больших скоростях.

Для выяснения типа режима нужно рассчитать число Рейнольдса Re и сравнить его с критическим Reкр.

Число Рéйнольдса Re — это безразмерный критерий, вычисляемый по формулам:

— для напорных потоков

Re =vd/n,

где d — внутренний диаметр напорного трубопровода;

— для безнапорных потоков

Re =vR/n,

где R — гидравлический радиус безнапорного потока, м (см. с. 14).

Критическое число Рейнольдса Reкр — это число Рейнольдса, при котором наступает смена режима движения.

Для напорных потоков

Reкр=2320,

для безнапорных потоков

Reкр » 500.

Упрощённо режим движения потока можно определить по шкале чисел Рейнольдса (см. рис. 12). Рассмотрим пример с напорной водопроводной тру­бой, у которой d=20 мм, v=1 м/с, n =10-6 м2/с. Для потока в дан­ной трубе число Рейнольдса составит:

Re=1×0,02/10-6 = 20000.

Число 20000 больше, чем Reкр=2320 (для напорных потоков) и на рис.12 оно находится в правой части шкалы, следовательно, режим потока турбулентный и все дальнейшие гидравлические расчёты должны проводиться только по зависимостям и формулам для этого ре­жима.

Расчёт напорных потоков

Расчёт напорных потоков сводится к нахождению неизвестных расходов q , скоростей v или потерь напора (разности напоров) DH. Для трубопроводов определяются их внутренние диаметры d.

Общие потери напора (или разность напоров) определяются по формуле Вéйсбаха

,

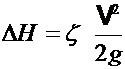где z — коэффициент гидравлического сопротивления.

Скорость потока связана с расходом соотношением вида

v=q/w ,

где w — площадь живого сечения потока. Например, для трубы круглого сечения w=pd2/4.

Таким образом, приведённые зависимости связывают величины DH, v, q, w, d, что позволяет рассчитать любой напорный поток. Значения коэффициента z принимаются в зависимости от вида определяемых потерь напора (линейных или местных).

Общие потери напора DH (м)в любом потоке представляют собой сумму линейных hl и местных hм потерь:

.

Линейные потери напора hl возникают на прямых участках труб (рис. 13,а). В литературе иногда встречаются другие варианты названий hl : потери напора по длине; потери напора на трение; путевые потери напора. Величина hl определяется по формуле Вéйсбаха в такой записи:

.

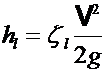Здесь коэффициент линейного гидравли­ческого сопротивления нахо­дится так:

,

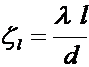где l — коэффициент гидравлического трения;

l — длина прямолинейного участка трубопровода.

Коэффициент гидравлического трения l зависит от режима дви­жения потока — ламинарного или турбулентного (см. рис. 12).

При ламинарном режиме

l = 64 / Re.

При турбулентном режиме

,

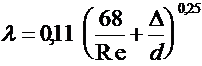где D — абсолютная шероховатость стенок трубопроводов. Например, у старых стальных труб D » 1,5 мм.

Гидравлическим уклоном i называется отношение линейных потерь напора hl к длине потока l (см. рис. 13, а):

i = hl / l.

Местные потери напора hм возникают в местах резкой дефор­мации потока: на поворотах труб, в местных сужениях или расширениях, тройниках, крестовинах, в кранах, вентилях, задвижках. На напорной ли­нии они изображаются в виде падающего скачкообразного участка hм (см. рис. 13,б).

Формула Вéйсбаха для местных потерь напора имеет вид

,

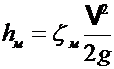где zм — коэффициент местного гидравлического сопротивле­ния. Он при­нимается для конкретного участка деформации потока (пово­рота, крана и т. д.) по справочным данным.

Гидравлический удар

Гидравлический удар представляет собой явление импульсивного из­менения давления, происходящее в напорных трубопроводах. Напри­мер, если резко закрыть водопроводный кран (рис. 14), то вода, дви­жущаяся со скоростью v, вынуждена так же резко остановиться. Однако из-за наличия инерционных сил движущейся жидкости перед краном возникнет ударное повышение давления величиной Dp, которое начнёт распро­страняться со скоростью звука vзв в воде в обратную сторону и может привести к авариям на трубопроводах.

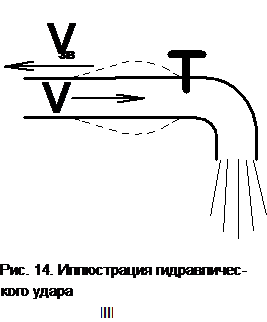
Величину Dp (Па) при гидравлическом ударе можно рассчитать по формуле :

Dp = r vvзв ,

где r — плотность жидкости, кг/м3.

Расчёт безнапорных потоков

Расчёт безнапорных потоков состоит в решении совместной задачи о про­пуске расхода q при допустимых скоростях потока v и геометрических уклонах iгеом днища труб, каналов и т. д. Безнапорные (со свободной по­верхностью) потоки наблюдаются в канализационных трубах, дорожных лотках, каналах; в природе — в реках, ручьях.

При расчёте безнапорных потоков вводится допущение о равно­мерном движении потока: геометрический уклон дна iгеом считается рав­ным уклону свободной поверхности (пьезометрическому уклону) и гидра­влическому уклону i . Другими словами, поверхность дна 1, свободная по­верхность потока 2 и напорная линия 3 параллельны друг другу (рис. 16). Это упрощает расчёт, так как определяя гид­равлический i, автоматически находят уклон дна iгеом.

Подчеркнём, что безнапорный поток имеет напоры! Дело в том, что термин «безнапорный» является традиционным, правильнее же его на­зывать «поток со свободной поверхностью». Например, на рис. 16 в точках потока А и В напоры существуют, и их отметки могут быть за­ре­гистрированы трубками Питó соответственно НА и НВ. Разность на­поров НА – НВ равна линейной потере напора hl на участке потока длиной l. Величина hl по принятому допущению равна Dz — разности высотных отметок дна в начале и конце участка, так как i = hl /l , iгеом = Dz/l, а i = iгеом.

Местные потери напора hм возникают в безнапорных потоках так ­же, как и в напорных, в местах резкой деформации потока: на поворотах, в тройниках, крестовинах, местных сужениях и т. д. Однако в расчётах без­напорных потоков величины hм обычно не учитывают.

При проведении гидравлического расчёта безнапорных потоков вво­дятся ограничения по скорости v (м/с), наполнению h/d (см. рис. 7,в) и уклону iгеом. Например, при расчёте канализационных труб должны быть выполнены три таких ограничения:

где dмм — внутренний диаметр трубы в мм.

Для расчёта безнапорных потоков широко применяется формула Шезú:

,

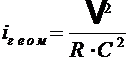где R — гидравлический радиус (м); С — коэффициент Шезú.

Коэффициент Шезú можно определить по формуле Маннинга

,

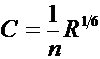где n — коэффициент шероховатости стенок трубы или канала;

R — гидравлический радиус, подставляемый в метрах.

Скорость потока связана с расходом соотношением вида

v = q/w.

Таким образом, приведённые формулы позволяют осуществлять гидрав­личе­ский расчёт любых безнапорных потоков. Обычно для расчётов используются вспомогательные таблицы или номограммы, составленные на основе формулы Шези.

Отметим, что формула Шези справедлива для потоков с турбулентным режимом. Таких потоков на практике подавляющее большинство.