324
Сравнение сотых и тысячных, десятых и тысячных долей про-
дится так же, как сравнение десятых и сотых долей. На кон-
|тных примерах (с мерами длины, стоимости, массы), а затем и
1тем отвлеченных рассуждений учащиеся убеждаются, что, на-
ВИмер, 0,1=0,10=0,100; 0,7=0,70=0,700 и т. д. и, наоборот,
[10=0,1; 0,70=0,7 и т. д.
Учитель обращает внимание учащихся на то, что нули, приписные в долях дроби справа от значащей цифры, не влияют на Ьобь. Отсюда можно подвести учащихся к понятию о сокраще-]|и десятичных дробей.
Сокращение десятичных дробей На примерах и практических упражнениях с метровой линей-ОЙ, квадратом, разделенным на 100 равных квадратов и 10 рав-ых полос, учащиеся убедились, что если дробь, например 0,30, вписать без нуля справа, т. е. 0,3, то дробь не изменится, но она римет более простой вид: 0,30=0,3. Запишем 0,30 со знаменате-
30 3
ем: - Г7Т7Г. Сократим эту дробь на 10, получим дробь -пг=0,3.
^ Допустим дана дробь 1,70. Эту дробь учащимся можно покапать на рулетке: 1 м 70 см, или 1,70 м, но это и 1 м 7 дм, т. е. 71,7 м, значит, 1,7 м=1,70 м, а теперь эти дроби запишем без наименований 1,70=1,7. Учащиеся еще раз убеждаются, что если в десятичной дроби отбросить 0 после значащей цифры, то величина этой дроби не изменяется.
Далее объясняем сокращение десятичной дроби, опираясь на знания учащихся о сокращении обыкновенной дроби.
Допустим, надо сократить дробь 1,70. Вначале учащиеся записывают эту дробь со знаменателем; а затем сокращают ее: 1,70=1-^=1-^=1,7; 1,70=1,7; 4,500=4,5; 72,010=72,01. Следовательно, отбрасывая один нуль после значащей цифры, мы сокращаем дробь на 10 (соответственно объясняем, что если отбрасываются два нуля, то дробь сокращается на 100:
0,100=0,1, так как -^=-^=0,1.
Приведение десятичных дробей к общему знаменателю
Учащиеся уже умеют сравнивать десятичные дроби, знают правило сравнения дробей по разрядам, но легче сравнивать дроби тогда, когда они выражены в одних и тех же десятичных долях, т. е. имеют
325
общий знаменатель." "Например, дроби 0,50 и 0,35 имеют общий мена: 0,50>0,35, так как 50 сотых больше 35 сотых, удобства вычислений дроби также выражают в одинаковых до, т. е. приводят к наименьшему общему знаменателю.
Учащиеся знают, что нуль, приписанный справа, дроби не меняет, т. е. 0,3=0,30=0,300. Увеличивая числитель, мы одмо| менно во столько же раз увеличиваем знаменатель.
Допустим, даны две дроби 0,2 и 0,40, их надо выразить в один! вых долях. Это значит, что дробь 0,2 надо выразить в сотых дол 0,2=0,20. Дроби 0,20 и 0,40 имеют одинаковый знаменатель I Значит, надо уравнять после запятой число знаков (цифр) путем п писывания нулей справа. Так же выражают в одинаковых дс^ дроби 5,6 и 0,75. Общий знаменатель этих дробей 100. Дроби 5, 0,75 теперь будут выглядеть так: 5,60 и 0,75.
В целях дифференциации понятий выразить дроби в одина вых долях и выразить дроби в более крупных долях предлагаю' упражнения вида:
1) сократить дроби: 110,80; 10,800; 4,40; 25,070; ,
2) привести дроби 10,8 и 10,83; 14,1 и 18,206; 17,85 и 41,0(|
63,486 и 1,08 к общему знаменателю;
3) сократить дроби: 10,80; 10,830; 14,10; 15,040; 80,<
71,060; 20,700.
Запись чисел, полученных при измерении величин, в виде десятичной дроби
В быту, в учебных мастерских и на производственных предприятиях учащимся приходится сталкиваться с выражением чисел, обозначающих длину, массу, стоимость и другие величины, десятичной дробью и наоборот. Начать изучение этой темы следу ет с выражения мер длины стоимости и массы десятичной дробью и наоборот. Например, 1 дм — это одна десятая доля метра, следовательно, 1 дм=0,1 м. На основании этого можно составить! такую табличку:
1 дм=0,1 м,
2 дм=0,2 м
5 дм=0,5 м
15 дм=1,5 м, так как 10 дм — это целый метр.
По аналогии с этим можно провести рассуждения и записать десятичными дробями числа, выраженные в других мерах. Например: 326
' 1 к.=0,01 р.
2 к.=0,02 р.
15 к.=0,15 р.
125 к. = 1,25 р.
1 г=0,001 кг
5 г=0,005 кг
18 г=0,018 кг
235 г=0,235 кг
При записи чисел, обозначающих длину, стоимость, массу и др., десятичной дробью следует соблюдать определенную последовательность, учитывая степень трудности выражения этого числа десятичной дробью. Вначале следует предлагать учащимся числа, выраженные одной единицей мер длины, стоимости, массы и др., а затем — двумя, причем вначале единичное отношение мер должно равняться 10. Например:
2 дм=0,2 м
3 см=0,3 дм
7 мм=0,7 см
3 м 5 дм=3,5 м
7 дм 5 см=7,5 дм
1 см 8 мм=1,8 см и т. д.
Затем надо брать такие числа, где единичное отношение мер равно 100. Например:
1 м 12 см=1,12 м 8 р. 75 к.=8,75 р. 3 ц 8 кг=3,08 ц
1 см=0,01 м 5 к.=0,05 р. 25 к.=0,25 р.
Наконец, берутся такие числа, где единичное отношение мер равно 1000. Например:
1 м=0,001 км
2 г=0,002 кг
15 кг=0,015 т
17 км 350 м= 17,350 км 3 кг 725 г=3,725 кг 8 т 600 кг=8,600 т
Особое внимание обращается на такие случаи записи чисел, обозначающих длину, стоимость, массу и др., десятичной дробью, в которых в десятичной дроби десятичные доли разряда равны нулю. Например, при записи десятичной дробью следующих чисел: 8 к., 5 р., 6 к., 3 м 4 см, 7 км 80 м, 8 т 30 кг. Записывается так: 8 к.=0,08 р., так как 1 к.=0,01 р. 5 р. 6 к.=5,06 р.; 3 м 4 см= =3,04 м, 7 км 80 см=7,080 км=7,08 км; 8 т 30 кг=8,030 т=8,03 т.
Запись десятичной дроби числами, полученными от измерения величин
В практике нередко требуется десятичную дробь записать в виде целого числа с одним или двумя наименованиями мер. Чтобы учащиеся могли выполнить это преобразование, необходимо использование наглядных пособий и соблюдение определенной последова-
327
тельности. Сначала следует вспомнить соотношение единиц мер рассмотреть те десятичные дроби, которые имеют знаменатель 10,|
1 м=10 дм 0,1 м=1 дм 0,5 м=5 дм 1,7 м=1 м 7 дм
1 дм=10 см
0,1 дм = 1 см
0,3 дм=3 см
10,4 дм=10 дм 4 см
Затем рассматриваются дроби со знаменателями 100, 10001 т. е. с сотыми и тысячными долями. Например: 0,8 р.=80 к.| 2,5 м=250 см; 0,3 кг=300 г.
ДЕЙСТВИЯ НДД ДЕСЯТИЧНЫМИ ДРОБЯМИ Сложение и вычитание десятичных дробей
Изучение сложения и вычитания десятичных дробей опирается на знание соответствующих действий с целыми числами.
Изучать действия сложения и вычитания целесообразно парал лельно, т. е. после каждого случая сложения давать соответствую щий по трудности случай вычитания
Применение наглядных пособий и дидактического материала при изучении арифметических действий с десятичными дробями ограничено.
Средством наглядности служит сама запись арифметических примеров, особенно запись в столбик.
Итак, прежде чем знакомить учащихся со сложением и вычитанием десятичных дробей, необходимо повторить сложение и вычитание целых чисел и обыкновенных дробей.
Последовательность и приемы вычисления
1. Сложение целого числа с десятичной дробью: 3+0,5;
4+0,13; 15+1,075.
2. Вычитание целого числа из десятичной дроби: 7,5—4; 7,85—3.
Действия в обоих случаях выполняются устно (если целые
числа небольшие). До сознания учащихся необходимо довести, что целые складываются с целыми или из целого числа вычитается целое, а дробная часть не изменяется. В этом случае можно сопоставить сложение целого числа с обыкновенной дробью:
3+0,5 и
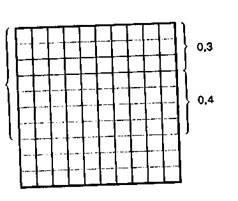
0,7
3. Сложение и вычитание десятичных дробей с одинаковым числом знаков без перехода через разряд:
0,3+0,4 0,14+1,25
7,4-1,3 3,42-1,31
3,124+7,835 4,356-2,135
Рис. 29
Действия сложения и вычитания можно проиллюстрировать на метровой линейке, разделенной на дециметры и сантиметры, или на квадрате (рис. 29), разделенном на 10 равных полос и 100 клеток.
0,3+0,4=0,7 0,7-0,4=0,3
Учащиеся должны уяснить, что действия над десятичными дробя
ми выполняются по аналогии с действиями над целыми числами,
т. е. складываются и вычитаются одноименные разрядные единицы
или доли единицы. Если складываются и вычитаются десятичные
дроби, число знаков в которых не превышало двух, то действие
выполняется устно, если число знаков выше двух, то действие запи
сывается в столбик. Важно провести аналогию между записью в
столбик примеров на многозначные числа и десятичные дроби и
показать сходство и различие в записи и приемах вычислений:
. 3456 3,,285
+ 4243 + 4.243 ~ 9143 ~ 9,143
7699 7,,142
4. Сложение и вычитание десятичных дробей с разным числом знаков без перехода через разряд:
3,7+0,235 3,935-3,7
3,7+1,21 4,91-3,7
0,71+5,246 5,956-0,71
При решении примеров такого вида учащиеся допускают ошибки, складывая или вычитая доли разных разрядов. Поэтому на первых порах следует приводить компоненты к общему знаменателю, приписывая нули справа: 3,935—3,7 записывается так:
3,935 ~ 3.700
329
328
5. Сложение и вычитание с переходом через разряд:
а) сложение десятичных дробей, когда в результате сложе»
десятых долей получается единица: 0,8+0,2;
б) вычитание десятичной дроби из единицы (1—0,8):
в) сложение
и вычитание десятичных дробей с переходом че|
разряд в одном разряде:
. 7,23 + 0,48
0,324 _7,43 7,490 0,18
_ 15,295 4,800 _ 7,045 _ 7,146 + 5.235
г) сложение и вычитание десятичных дробей с переходом чер разряд в двух и более разрядах:
2,745 1,960
.3,75 + 4,25 Й. ОО
Ю 10
_ 8,00 3,43
0,785
1 1
. 0,735 + 1,870
2,605
Следует требовать записывать нули так, где нужно уравш число десятичных долей в компонентах действий сложения и читания.
Рассуждения при сложении проводятся так: «Сложение нач| наем с тысячных долей: 5 тысячных плюс 0 тысячных получитщ 5 тысячных, 5 пишем под тысячными долями, к 3 сотым прибавляем 7 сотых, получаем 10 сотых, 0 сотых пишем под сотыми, 1 десятую запоминаем; складываем десятые доли, 7 десятых и 8 десятых — будет 15 десятых, да еще 1 десятая — будет 16 десятых, 6 десятых пишем под десятыми, 1 целую запоминаем; складываем целые, целых 2. Сумма 2,605».
При вычитании рассуждения проводятся так: ю ю
5,135 ~ 0,243
4,892
«От 5 тысячных отнимаем 3 тысячных, будет 2 тысячных, записываем их под тысячными; из 3 сотых 4 сотых вычесть нельзя, занимаем одну десятую; в одной десятой содержится 10 сотых, прибавим к ним 3 сотых, будет 13 сотых, из 13 сотых вычитаем 4 сотых, получаем 9 сотых и записываем под сотыми; вычитаем десятые, но в уменьшаемом десятых не осталось, поэтому занима-330
одну целую, в одной целой 10 десятых, из 10 десятых вычита-•) 2 десятых, будет 8 десятых, подписываем их под десятыми, гвычитаем целые и подписываем их под целыми. Так же как и при ; выполнении действий с целыми числами, над разрядом, из которого занимаем единицу, ставим точку».
Необходимо также решать с учащимися сложные примеры на сложение и вычитание десятичных дробей, примеры со скобками, с неизвестными компонентами, проводить проверку действий. При •том следует подчеркнуть, что при выполнении действий с десятичными дробями используются как переместительный, так и сочетательный законы сложения, так же как и при выполнении действий с целыми числами.
Умножение и деление десятичных дробей
Прежде чем перейти к методике знакомства с умножением и делением десятичных дробей, следует заметить, что согласно программе по математике в школе VIII вида учащиеся знакомятся только с умножением и делением десятичной дроби на целое число. Случаи умножения и деления на десятичную дробь не рассматриваются.
Можно предложить следующую последовательность изучения умножения и деления десятичных дробей на целое число:
1) умножение и деление десятичных дробей на 10, 100, 1000;
2) умножение и деление десятичных дробей на однозначное
число;
3) умножение и деление десятичных дробей на круглые десятки;
4) умножение и деление десятичных дробей на двузначное
число.
Действия умножения и деления рассматриваются параллельно, так как каждому случаю умножения соответствует определенный случай деления. Это позволит сопоставить взаимно обратные действия, выявить сходство и различие, осуществить проверку одного действия другим.
Умножение десятичной дроби на 10, 100, 1000
При выводе правила об умножении десятичной дроби на 10, 100, 1000 целесообразнее всего опираться на знания учащихся об умножении обыкновенных дробей.
331
Например: 0,7x10=? Учитель, опираясь на знания учац просит записать первый множитель со знаменателем, т. е. об1 венной дробью, и произвести умножение: - п>гХ10=—™— =7, довательно, 0,7x10=7. Затем учитель обращает внимание щихся на первый множитель и на произведение (0,7 и 7) и пр
сравнить их. Он спрашивает: «Что произошло с запятой во.....
жителе, когда его умножили на 10? В какую сторону и на скольн знаков переместилась запятая во множителе при умножении на 10?
Затем надо рассмотреть еще один пример и снова ответить вопрос о перемещении запятой вправо после умножения десяти"] ной дроби на 10: 1,23-10=?
10=12,3
После рассмотрения еще двух-трех примеров и сравнения мне жителя и произведения некоторые учащиеся сами могут сделай вывод: при умножении десятичной дроби на 10 нужно перенест| запятую вправо на один знак.
Объяснение можно провести, используя нумерационную табл» цу. Запишем 0,7 в таблицу. Это число надо умножить на 10, т. I увеличить в 10 раз. Это значит, надо передвинуть данное число. нумерационной таблице на один разряд влево, будет 7. Реши] таким способом еще ряд примеров, учащиеся придут к выш| сформулированному правилу. Аналогично рассматривается умнс жение десятичной дроби на 100, 1000.
0,75-100 тЙо-100=75-^=^=7,5
0,
-^-1000=125
После того как ученики усвоят правило умножения на 10, 100, 1000, необходимо подвести их к выводу общего правила умножения десятичной дроби на единицу с нулями: при умножении десятичной дроби на число, выраженное единицей с нулями, нужно перенести вправо запятую на столько знаков, сколько нулей в множителе.
Учителю обязательно надо обратить внимание учащихся на то, что при умножении числа на 10, 100, 1000 каждый разряд произведения соответственно увеличивается в 10, 100, 1000 раз. Например: 7,95-10=79,5. Сопоставляя первый множитель и произведение, надо показать, что 7 единиц множителя увеличились в 10 раз и в произведении получилось 7 десятков, 9 десятых увеличились тоже в 10 раз и в произведении получилось 9 единиц, 5 сотых увеличились в 10 раз и в произведении получилось 5 десятых. 332
алогично рассматриваются примеры на умножение десятичной на 100, 1000.
оби на, .
\ Особое внимание нужно обратить на такие случаи умножения, которых в результате умножения десятичной дроби на 10, 100 ли 1000 в ответе получается целое число (учащиеся недоумева->т: умножали дробь, а получилось целое число).
Еще большую трудность вызывает решение таких примеров, в оторых в произведении нужно приписывать нули справа — исло знаков после запятой меньше, чем число нулей во втором ножителе, например: 0,5-100=50.
1 Для того чтобы учащиеся более осознанно относились к реше-ию подобных примеров, нужно время от времени сравнивать азряды первого множителя и произведения, например: 1,15-10=1,5. Рассуждать следует так: «Одну десятую увеличили 10 раз, получили одну целую, пять сотых увеличили в 10 раз, олучили пять десятых».
Полезны и такие упражнения:
Г Если в числе 4,54 перенести запятую вправо на один знак, то •число примет вид 45,4 Что же произошло с этим числом? Во "сколько раз увеличилось это число? Что произошло с единицами (с десятыми, сотыми долями)?
Если в числе 3,75 перенести запятую на два знака вправо, то что произойдет с числом? Во сколько раз увеличится число? Во сколько раз увеличится каждый разряд этого числа?
Если число 4,8 увеличить в 1000 раз, то для этого нужно перенести запятую на три знака вправо, но в первом множителе посыле запятой только один знак. В этом случае следует рекомендовать учащимся поставить три точки после запятой, например: 4,8x1000=48 , а затем на месте точек написать нули: 4,8-1000=4866.
Деление десятичной дроби на 10, 100, 1000
Деление десятичной дроби на 10, 100, 1000 рассматривается аналогично умножению (десятичные дроби записываются со знаменателем):
0,3 :10= А: 10=^=4=0,03; 0,3:10=0,03 0,7: 100=-^: ЮО=т^ш-=-Кщ=0,007; 0,7: 100=0,007
1,2: 1000-й' 1000=ТО^ОО =ЖШО=°-0012:
1,2:1000=0,0012
333
Сначала делается вывод о делении десятичной дроби на затем на 100 и затем на 1000. В итоге учащиеся подводят общему правилу деления десятичной дроби на число, выражен» единицей с нулями.
Так же как и при умножении десятичных дробей, обращает внимание на то, что при делении числа на 10, 100, 1000 ка> разряд частного уменьшается соответственно в 10, 100, 1000
Учитывая, что при умножении и делении десятичных дробей 10, 100, 1000 умственно отсталые школьники допускают много ошибок, в частности путают, куда переносить запятую — влено или вправо, необходимо чаще решать примеры, в которых бы действия умножения и деления сопоставлялись, например 7,85.10-78,5; 78,5:10=7,85; 78,5-100=7850; 78,5:100=0,785
Полезно, так же как и при умножении, ставить перед запятой^ (слева от запятой) столько точек, сколько нулей в делите; 7,45:100=0,0745.
Умножение и деление десятичных дробей на целое число
Умножение и деление десятичных дробей на целое число тесно связано с умножением и делением целых чисел. Чтобы подвести учащихся к пониманию того, как производится умножение десятичной дроби на целое число, и сделать обобщение в виде правила, необходимо начать с рассмотрения простейших случаев (при этом учитель должен воспользоваться тем, что учащиеся уже имеют понятие о действии умножения), например: 1,2-3=. В этом выражении действие умножения заменяется действием сложения: 1,2-3 = 1,2+1,2+1,2=3,6, 1,2-3=3,6. Внимание учащихся надо обратить на то, что сначала умножается целое число на множитель и это произведение целых отделяется запятой, а затем умножаются десятые доли на множитель. Подобные случаи умножения (без перехода через разряд ни в одном разряде) выполняются устно. Случаи умножения с переходом через разряд выполняются в столбик:
Множители перемножаются как целые числа и в полученном произведении отделяется запятой справа столько цифр, сколько десятичных знаков в первом множителе.
334
Примеры на умножение десятичной дроби на целое число подираются в той же последовательности, что и примеры на умно-1(ение целых чисел.
• Наибольшие трудности для учащихся представляют примеры, в Которых в первом множителе один или несколько десятичных раков равны нулю, а также примеры, в которых в произведении ^случается нуль целых.
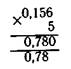
,0,005
Например: Х0,032 38
0,285
« Подобные примеры надо чаще предъявлять учащимся, повторив предварительно правила умножения нуля на целое число и целого
числа на нуль.
При делении десятичной дроби на целое число также следует соблюдать определенную последовательность:
1.Все разряды делимого делятся на делитель без остатка:
6,48:2 = ?. Делим на 2 сначала целые, отделяем целые в частном
запятой, потом делим десятые доли и, наконец, сотые доли:
6,48:2=3,24. Такие примеры решаются устно.
2. Целое или какая-либо из долей делимого не делится нацело
на делитель: 4,86:3.
Делим 4 целых на 3. В частном получаем единицу, отделяем ее запятой. В остатке осталась единица. Дробим ее в десятые доли и прибавляем еще 8 десятых. 18 десятых делим на 3, получаем 6 десятых. Далее 6 сотых делим на 3, получаем 2 сотых. Частное равно 1,62.
3. Особые случаи деления, когда в частном полу-
чаются нули:
1) 0,012:4=0,003
2) 12,432:6=?
3) 1:8=?
1,000 ' 8
12,432 '12
20 16
43 42
40 40
12 12
8 ОД25~
335
4. Деление десятичной дроби на двузначное число:
|ной. Для этого нужно, чтобы знаменатель этой дроби стал ен 10, 100 или 1000. В десятых долях эту дробь выразить нельзя, К как 10 не делится на 4 нацело. Посмотрим, нельзя ли вылить эту дробь в сотых долях: 100:4=25. Значит, и числитель,
I Ч
[знаменатель дроби -т надо умножить на 25 (дополнительный
о о ос "71л
.ожиСледовательно, 4'=:Т^5"=ТШ=^!^^' Выразим
обь - д - в десятичных долях. Знаменане подходит, так как
О не делится на 8 нацело, знаменатоже не подходит по
рй же причине, попробуем взять знамена:8=125 (до-
Олнительный множиСледовательно.
5_5>125_ 625 _
—- ~ . Л г1 1ЛГ>Г>
Умножение и деление десятичных дробей, так же как и сое ветствующие действия с целыми числами, изучаются параллельн! Каждое действие учащиеся учатся проверять обратным ему дейс] вием.
Решаются также примеры, в которых содержатся действия вой и второй ступени со скобками, чтобы поупражнять учащихс в применении правил порядка действий. Кроме того, следует пре ложить и примеры на нахождение неизвестного множимого, неи| вестного делимого.
Запись десятичной дроби в виде обыкновенной и наоборот
С выражением десятичной дроби в виде обыкновенной учащи ся уже сталкивались неоднократно. Во-первых, образование дес! тичной дроби рассматривалось как частный случай обыкновение дроби, у которой знаменатель — единица с нулями, во-вторыэ десятичную дробь в виде обыкновенной учащиеся выражали пр знакомстве с действиями над десятичными дробями. Запись дес>1 тичной дроби в виде обыкновенной сводится к записи десятично!
3 7
дроби со знаменателем, например: 0,3=тп; 0.0?=7731
Й7Ч '
1,873=1^ и т. д.
Обратное упражнение, т. е. запись обыкновенной дроби в виде десятичной, выполняется так:
У обыкновенной дроби -^ знаменатель дроби 5, у десятичной
же дроби знаменатель должен выражаться единицей с нулями, т. е. 10, 100, 1000 и т. д. Подбираем такое число, при умножении на которое числа 5 получалось бы 10, 100, 1000, т. е. знаменатель дроби выразился бы единицей с нулями. Если 5 «2, то получится! 10. Чтобы дробь не изменилась, надо и числитель умножить на 2.<
1 1 • 2 2 3
Следовательно, 5'=5Т2":=То':=^'^' Запишем дробь -? в виде деся-
336
Но не всегда этим способом можно (при замене обыкновенной дроби десятичной) выразить знаменатель обыкновенной дроби 1 с несколькими нулями. Возьмем, например, дробь - я-. Попробуем взять знаменаОн не подходит, так как нельзя в данном случае получить дополнительный множине делится нацело на 3. То же получим, если возьмем знамена, 1000. Следовательно, дробь -^ нельзя этим способом выразить десятичной дробью.
Существует второй способ замены обыкновенной дроби десятичной. Всякую обыкновенную дробь можно рассматривать как
з
частное от деления числителя на ее знаменатель. Возьмем дробь -^. Ее можно рассматривать как частное от деления 3 на 4. Выполним деление:
Рассуждение: «3 на 4 не делится нацело. В частном пишем нуль целых и ставим после нуля запятую. Раздробляем 3 в десятые доли. 30 десятых делим на 4. В частном пишем 7 десятых. В остатке 2 десятых. Раздробим 2 десятых в сотые доли. Получим 20 сотых. Делим на 4. В частном 5 сотых.
3
,0,75
Итого в частном 0,75. Следовательно, - т-=0,75». Проверка. Нужно частное умножить на делитель. В произведении должно получиться число, равное делимому:
X
0,75-4=3.
После рассмотрения еще нескольких примеров учащиеся ны сами сделать вывод о том, как обыкновенную дробь зал десятичной.
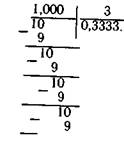
«Вернемся к дроби ^-. Мы видели| , 1 дробь т нельзя заменить десятичной п«
способом. Попробуем заменить ее десяти вторым способом, т. е. делением числите^ знаменатель. Если будем продолжать д дальше, то увидим, что всегда в остатке о единица, а в частном 3. Деление можно! должить бесконечно. Но обычно его пред
---- ют, делят до первого, второго или тре!
знака после запятой, например: 1:3=0,33| В данном случае деление закончили на тысячных долях. ТМ показывают, что деление можно продолжить и дальше. 0,333..74 приближенное, неточное значение дроби т?. Можно предложит!
учащимся обратить в десятичные еще ряд обыкновенных дробей
21513 п -
3"' Б"' !)' 7' 7 и т' д' Получаются приближенные десятичные дроом После рассмотрения замены различных обыкновенных дроои1 десятичными учащиеся убеждаются, что одни обыкновении! дроби можно точно выразить десятичными — в этом случае полу» чаются конечные десятичные дроби - г = 0,2 , другие же можнС заменить только бесконечными десятичными дробями
| = 0,333.. ^
Совместные действия с обыкновенными и десятичными дробями
После изучения обыкновенных и десятичных дробей программой предусмотрены совместные действия над дробями. Перед изучением этой темы следует повторить отдельно все действия над обыкновенными и десятичными дробями, устно и письменно закрепить замену обыкновенной дроби десятичной и наоборот. Все эти виды упражнений должны быть хорошо отработаны, иначе учащиеся при выполнении совместных действий с дробями столкнутся с непреодолимыми трудностями, что вызовет у школьников с нарушением интеллекта чувство беспомощности, негативное отношение к работе. 338
При выполнении совместных действий с десятичными и обыкновенными дробями в школе VIII вида, как показывает опыт, целесообразнее либо все обыкновенные дроби заменять десятичными и выполнять действия только над десятичными дробями, либо наоборот.
Сначала решаются задачи и примеры с двумя компонентами. Учитель, объясняя, как выполнить действие, должен обратить внимание учащихся на целесообразность замены дробей десятичными или обыкновенными. Например, в примере 0,45+-я - целесообразно дробь - д - заменить десятичной, так как это сделает вычисления более простыми. Если же 0,45 заменить обыкновенной дробью, то вычисления будут более громоздкими.
В этом учащихся следует убедить, предложив выполнить действия сначала в десятичных, а затем в обыкновенных дробях:
45
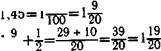1,45+^=?
!2&
Г=°'5 1,45+0,5=1,95
Сначала учитель подсказывает учащимся, с какими дробями целесообразнее выполнять действия.
По мере накопления опыта учащиеся сами должны выбирать наиболее удобные пути решения в каждом конкретном случае.
МЕТОДИКА ИЗУЧЕНИЯ ПРОЦЕНТОВ
Понятие о проценте дается учащимся специальной школы VIII вида после изучения десятичных дробей. Процент — это дробь со знаменателем 100, имеющая особое название (подобно ^ — половина) и особую форму записи (удд - — процент). Слово «процент» обозначается знаком %.
Десятичные дроби со знаменателем 100 наиболее удобны для вычислений, так как во многих мерах метрической системы встречается единичное отношение м=100 см, 1 р. = 100 к., 1 га=100а, 1 ц=100кг; следовательно, 1 см=0,01 м, 1 к.=0,01 р., 1 а=0,01 га, 1 кг=0,01 ц), таг часть числа обозначается так: 1%. Можно записать, что 1 см=0,01 м=1% метра, 1 к.=0,01 р. = 1% рубля, 1а=0,01 га = 1% гектара, 1 кг=1% центнера. В данном случае мы выразили полученные числа в процентах. Отвлеченные
339
т
числа также можно выразить в процентах. Учащимся это мож объяснить так: «1% — это -т^.частъ числа. Чему же равно и
1 100
число? Оно в 100 раз больше, т. е. тятт' 100=™*-=!. Знач!
если ^0 = 1%, то -^=1 = 100%, 2=200%, 5=500* 15=1500%» и т. д.
На основе понятия о проценте и умений выразить (записат числа в процентах необходимо объяснить значение часто встр чающихся на производстве и в быту выражений, например: «РаС чий выполнил норму по обработке деталей на 100%». Это озна«, ет, что рабочий обработал за смену то количество деталей, кот. рое было запланировано, например 150 деталей. Если рабоч! сделал меньше 150 деталей, то он не выполнил норму, т. е. в| полнил ее меньше чем на 100%. Если рабочий сделал болы 150 деталей, то он перевыполнил норму, т. е. выполнил ее болы чем на 100%.
Учащиеся знакомятся не только с выражением целого чис; но и десятичных дробей процентами.
В этом случае учитель при объяснении также исходит из определения процента: 0,01 = 1%, следовательно, 0,02=2%; 0,05=5%; 0,25=25%; 0,5=50%, так как 0,5=0,50=50%; 1,7=170%. На основании подобных рассуждений, наблюдений и сравнения деся-1 тичной дроби и числа, выражающего эту дробь в процентах, некоторые учащиеся могут сделать вывод: чтобы десятичную^ дробь заменить процентами, надо перенести за-! пятую вправо на два знака и поставить знак %. Вместо недостающих знаков ставятся нули. Обыкновенную дробь также можно выразить (заменить) процентами. Ее нужно для этого обратить в десятичную дробь и применить правило замены
десятичной дроби процентами, например: - г=0,8=80%; 2^=2,25=225%.
Учащихся школы VIII вида знакомят и с обратной задачей: выражением процентов в десятичных или обыкновенных дробях.
Рассуждения ведутся также исходя из понятия о проценте: 1%=0,01; 2%=0,02%; 40%=0,40=0,4; 100% = 1; 200%=2;
150% = 1,5; ^.=0,5=50%; ^=0,25=25%; -^=0,1 = 10%. 340
[ На основе наблюдений и сравнения числа процентов и дроби, выражающей это число, учащиеся подводятся к выводу: чтобы выразить проценты десятичной дробью или целым числом, надо запятую перенести на два знака влево и знак % не писать: 20%=0,2; 300%=3.
Решение задач на проценты
Программой школы VIII вида предусмотрено решение задач на нахождение одного и нескольких процентов от числа, а также нахождение числа по одному проценту.
Задачи на проценты не представляют собой ничего нового для учащихся по сравнению с ранее решавшимися задачами на нахождение одного и нескольких частей от числа и на нахождение числа по одной и нескольким частям. Поэтому, прежде чем решать задачи на проценты, надо повторять решение ранее решавшихся задач и довести до сознания каждого учащегося, что 1% — это тоже дробь (-тщ и 0,01] , но записанная особым
образом.
Сначала дается понятие вычисления 1% и нескольких процентов от числа и вырабатывается навык выполнения этих действий. Например, надо найти 1% от 200. Рассуждаем так: 1%=^о"-Значит, надо найти - тта- (т. е. взять 1 сотую) от 200, т. е.
200:100-1=2.
Учащиеся должны решить несколько таких примеров и на основе наблюдений сделать вывод: чтобы найти 1% от числа, надо это число разделить на 100. Только после этого учащиеся начнут решать задачи на нахождение 1% от числа типа: «Рабочий получает 1000 р. 1% от своего заработка он платит налог. Сколько денег рабочий платит?»
Решение.
1) Найдем 1% от 1000 р.
1%=-; - щ - от 1000 р. — это 1000 р.: 100.1 = 10 р.
Ответ. Рабочий платит налог 10 р.
Аналогично подходят и к решению задач на нахождение нескольких процентов от числа. Например, надо найти 5% от 200, т. е. - т от 200. Находим сначала 1%, т. е. -т долю от 200
341
(200:100-1=2), и берем 5 таких долей, т. е. 5%. Знач» 2 «5= 10. Вычисления записываются так: 200:100-5=10.
Учитель обязательно должен каждый раз спрашивать: «Что м получаем, когда делим число на 100? Почему умножаем на чис; процентов?» Это позволяет учащимся более сознательно относит ся к вычислениям.
Задачи на нахождение нескольких процентов от числа целес( образно решать сначала в два действия и только тогда, когд учащиеся осознанно будут относиться к записи решения задач сложным примером, содержащим два действия, можно будет заш сать действия в одну строку. Например: «В школу привезли 70 учебников. 9% учебников передали в библиотеку. Сколько учев ников передали в библиотеку?»
2-й способ записи решения. 1. Сколько учебников
передали в библиотеку?
700 уч.: 100-9=63 уч. Ответ. 63 учебника
передали в библиотеку.
1-й способ записи решения.
1. Чему равен 1% от числа
700 учебников?
700 уч.: 100=7 уч.
2. Сколько учебников переда
ли в библиотеку?
7 уч. • 9=63 уч. Ответ. 63 учебника передали в библиотеку.
Задачи на нахождение 1% от числа и на нахождение нескольких процентов от числа необходимо постоянно сопоставлять, находить черты сходства и различия.
Задачи на нахождение числа по одному проценту обратим задачам на нахождение 1% и нескольких процентов от числа. 11оэтому нужно сначала рассмотреть прямую задачу, решить ее, а потом из нее образовать обратную ей задачу, решить ее и сопоставить решение прямой и обратной задач.
Прямая задача: «В саду посадили 200 саженцев фруктовых де-, ревьев. 1 % саженцев погиб. Сколько саженцев фруктовых деревьев погибло?» 1 % от 200 — это 200:100=2 (саж.).
Обратная задача: «В саду посадили саженцы фруктовых деревьев. 2 саженца погибло, что составляет 1 % от всех посаженных деревьев. Сколько саженцев фруктовых деревьев посадили в саду?»
Рассуждение проводим так: «2 саженца — это 1% всех деревьев, а все саженцы составляют 100%, т. е. их число в 100 раз больше 2, поэтому нужно 2*100. Следовательно, если 1% составляет 2 саженца, то 100% составляет 2 • 100=200 (саженцев)».
Решив еще несколько аналогичных задач и примеров на нахождение числа по одному проценту и сопоставив их с прямыми задачами и примерами, можно подвести учащихся к выводу: чтобы найти число по 1%, нужно это число умножить на 100.
Часто встречаются задачи, в которых нужно вычислить число! процентов, превышающих 100%. Эти задачи имеют большое жиз-| ненно-практическое значение и часто встречаются.
Например: «Норма выработки рабочего — 400 деталей за смену. Он выполнил норму на 115%. Сколько деталей он сделал?»
Находим 115% от 4дет.: 100-115=460 дет.
Ответ. Рабочий сделал за смену 460 деталей.
Задачу можно решить и другим способом. Рассуждаем так: 400 деталей — это 100%. Рабочий выполнил норму на 115%, т. е. он перевыполнил план на 15% (115% —100% = 15%). Найдем, сколько деталей рабочий сделал сверх плана. Надо найти 15% от 400 деталей. 400 дет.: 100-15=60 дет. Далее узнаем, сколько деталей сделал рабочий за смену: 400 дет.+60 дет.=460 дет.
|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 |
Основные порталы (построено редакторами)