Построить эпюру изгибающих моментов и выполнить расчет бруса на прочность, при условии, что предельно допустимое нормальное напряжение при изгибе: [σ] ≤ 100 МПа. Брус считать невесомым.

Распределенная нагрузка q | Поперечная сила F | Диаметр бруса d |
100 Н/м | 200 Н | 15 см |
3.4.2. Примеры билетов для контрольных работ
Контрольные задания для рубежного контроля могут выдаваться в виде тестов или билетов, включающих один теоретический вопрос и задачу. Ниже представлены примеры билетов для контрольной работы № 2 по теме «Сопротивление материалов».
Билет № 1
Теоретический вопрос:
Раскройте смысловое содержание гипотезы плоских сечений (гипотезы Бернулли).
Задача:
При помощи эпюры напряжений определить наиболее напряженный участок двухступенчатого круглого бруса, нагруженного продольными силами F1 и F2. Найти удлинение бруса, если известно, что он изготовлен из алюминиевого сплава, имеющего модуль упругости Е = 0,7 х 1011 Па.
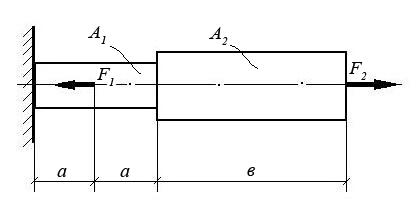
F1 | F2 | А1 | А2 | a | в |
10 кН | 20 кН | 0,1 м2 | 0,2 м2 | 1 м | 3 м |
Билет № 2
Теоретический вопрос:
Перечислите основные виды нагрузок и деформаций. Приведите примеры.
Задача:
При помощи эпюры напряжений определить наиболее напряженный участок двухступенчатого круглого бруса, нагруженного продольными силами F1 и F2. Найти удлинение бруса, если известно, что он изготовлен из стали, имеющей модуль упругости Е = 2,0 х 1011 Па.

F1 | F2 | А1 | А2 | a | в |
15 кН | 40 кН | 0,3 м2 | 0,5 м2 | 2 м | 5 м |
Билет № 3
Теоретический вопрос:
Назовите виды деформаций, при которых в сечении возникают продольные силы.
Задача:
При помощи эпюры напряжений определить наиболее напряженный участок двухступенчатого круглого бруса, нагруженного продольными силами F1 и F2. Найти удлинение бруса, если известно, что он изготовлен из меди, имеющей модуль упругости Е = 1,2 х 1011 Па.

F1 | F2 | А1 | А2 | a | в |
1500 Н | 1200 Н | 0,05 м2 | 0,12 м2 | 0,5 м | 2,0 м |
Билет № 4
Теоретический вопрос:
При каком виде деформации в сечении возникает только поперечная сила? Приведите примеры.
Задача:
При помощи эпюры напряжений определить наиболее напряженный участок двухступенчатого круглого бруса, нагруженного продольными силами F1 и F2. Найти удлинение бруса, если известно, что он изготовлен из алюминиевого сплава, имеющего модуль упругости Е = 0,7 х 1011 Па.

F1 | F2 | А1 | А2 | a | в |
10 кН | 20 кН | 0,1 м2 | 0,2 м2 | 1 м | 3 м |
Билет № 5
Теоретический вопрос:
При каком виде деформации в сечении возникает только крутящий момент? Приведите примеры.
Задача:
Построить эпюру изгибающих моментов и выполнить расчет бруса на прочность, при условии, что предельно допустимое нормальное напряжение при изгибе: [σ] ≤ 100 МПа. Брус невесомый.
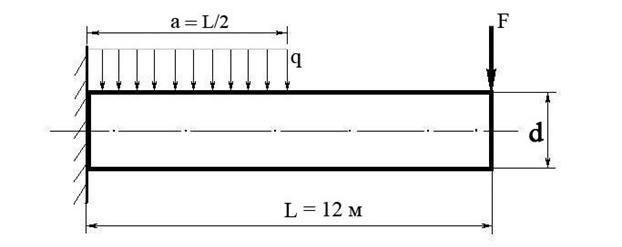
F | q | Диаметр бруса d |
100 Н | 100 Н/м | 10 см |
Билет № 6
Теоретический вопрос:
Сформулируйте закон Гука при растяжении и сжатии. Запишите его математически в виде формулы.
Задача:
Построить эпюру изгибающих моментов и выполнить расчет бруса на прочность, при условии, что предельно допустимое нормальное напряжение при изгибе: [σ] ≤ 100 МПа. Брус невесомый.
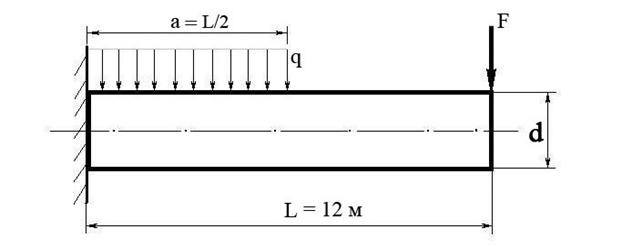
F | q | Диаметр бруса d |
300 Н | 50 Н/м | 8 см |
Билет № 7
Теоретический вопрос:
При каком виде деформации в сечении возникает только изгибающий момент? Приведите примеры.
Задача:
Построить эпюру изгибающих моментов и выполнить расчет бруса на прочность, при условии, что предельно допустимое нормальное напряжение при изгибе: [σ] ≤ 100 МПа. Брус невесомый.

F | q | Диаметр бруса d |
300 Н | 40 Н/м | 0,05 м |
Билет № 8
Теоретический вопрос:
Сформулируйте закон Гука при сдвиге. Запишите его математически в виде формулы.
Задача:
Построить эпюру изгибающих моментов и выполнить расчет бруса на прочность, при условии, что предельно допустимое нормальное напряжение при изгибе: [σ] ≤ 100 МПа. Брус невесомый.

F | q | Диаметр бруса d |
100 Н | 200 Н/м | 0,1 м |
Билет № 9
Теоретический вопрос:
Сформулируйте закон Гука при чистом изгибе, запишите в виде формулы.
Задача:
Построить эпюру изгибающих моментов и выполнить расчет квадратного бруса на прочность, при условии, что предельно допустимое нормальное напряжение при изгибе: [σ] ≤ 100 МПа. 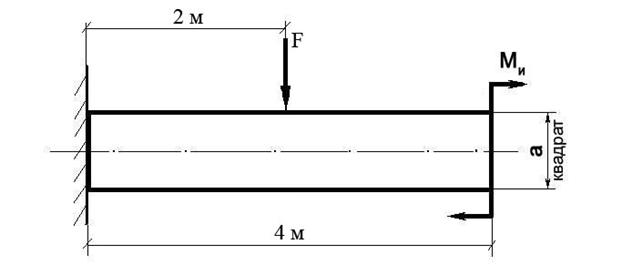
F | Ми | a |
100 Н | 100 Н/м | 0,1 м |
Билет № 10
Теоретический вопрос:
Что такое «модуль упругости первого рода»?
Задача:
Построить эпюру изгибающих моментов и выполнить расчет квадратного бруса на прочность, при условии, что предельно допустимое нормальное напряжение при изгибе: [σ] ≤ 100 МПа. 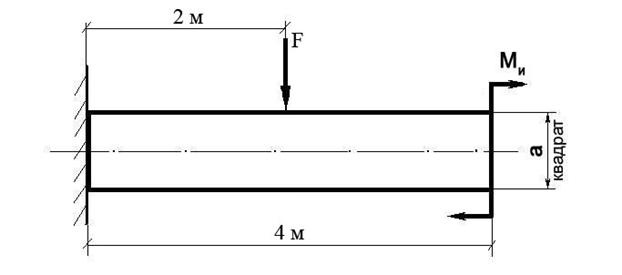
F | Ми | a |
200 Н | 20 Н/м | 0,08 м |
Билет № 11
Теоретический вопрос:
Какова зависимость между продольной и поперечной деформациями при растяжении? Формула Пуассона и ее пояснение.
Задача:
Построить эпюру изгибающих моментов и выполнить расчет квадратного бруса на прочность, при условии, что предельно допустимое нормальное напряжение при изгибе: [σ] ≤ 100 МПа. 
F | Ми | a |
150 Н | 10 Н/м | 0,1 м |
Билет № 12
Теоретический вопрос:
Что такое «жесткость» и «прочность» детали? Для чего проводят расчеты на жесткость и прочность?
Задача:
Построить эпюру изгибающих моментов и выполнить расчет квадратного бруса на прочность, при условии, что предельно допустимое нормальное напряжение при изгибе: [σ] ≤ 100 МПа. 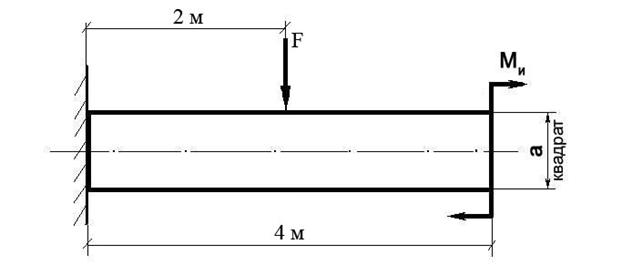
F | Ми | a |
50 Н | 50 Н/м | 0,05 м |
Билет № 13

|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 10 |





