Вес бруса не учитывать.
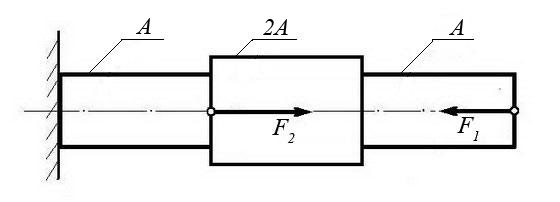
Сила F1 | Сила F2 | Площадь сечения А |
10 кН | 25 кН | 0,2 м2 |
Задача №3:
Используя закон Гука, найти удлинение ΔL однородного круглого бруса, если известно, что он изготовлен из алюминиевого сплава, имеющего модуль упругости Е = 0,4 ×105 МПа.
Вес бруса не учитывать.
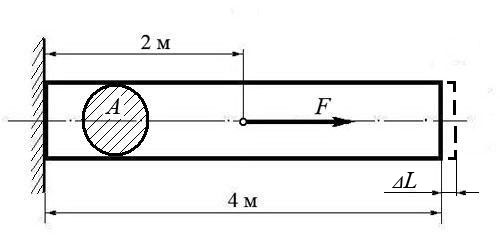
Сила F | Площадь сечения А |
200 кН | 0,01 м2 |
(Ответ: общее удлинение бруса ΔL = FL / (EA) = 2×105 × 2 / 0,4×1011 × 0,01 = 10-3 м или ΔL = 1,0 мм)
Задача №4:
Однородный брус длиной L и поперечным сечением площадью А нагружен растягивающей силой F. Используя закон Гука, найти удлинение бруса ΔL, если известно, что он изготовлен из стального сплава, имеющего модуль упругости Е = 2,0 × 105 МПа.
Вес бруса не учитывать.
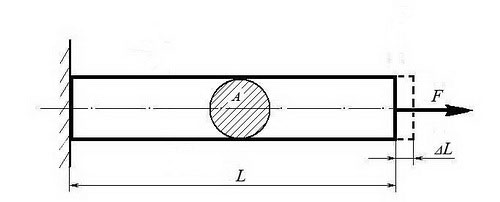
Сила F | Площадь сечения А | Длина бруса L |
500 кН | 0,05 м2 | 10 м |
(Ответ: удлинение бруса ΔL = FL / (EA) = 5×105 × 10 / 2×1011 × 0,05 = 5×10-4 м или ΔL = 0,5 мм)
Задача №5:
Однородный круглый брус жестко защемлен одним концом и нагружен внешними вращающими моментами Т1, Т2 и Т3.
Построить эпюру крутящих моментов и выполнить проверочный расчет бруса на прочность, при условии, что предельно допустимое касательное напряжение: [τ] = 30 МПа.
При расчете принять момент сопротивления кручению круглого бруса W ≈ 0,2 d3.
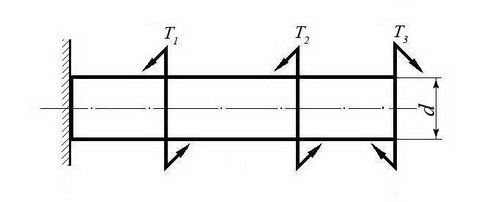
Вращающий момент Т1 | Вращающий момент Т2 | Вращающий момент Т3 | Диаметр бруса d |
30 Нм | 40 Нм | 30 Нм | 0,02 м |
(Ответ: максимальное касательное напряжение в брусе - 25 МПа, что меньше предельно допустимого, т. е. брус выдержит заданную нагрузку.)
Задача №6:
Однородный круглый вал нагружен вращающими моментами М1, М2, М3 и М4. Построить эпюру крутящих моментов в сечениях вала и определить наиболее напряженный участок.
С помощью формулы Мкр ≈ 0,2 d3 [τ] определить минимальный допустимый диаметр вала d из условия прочности.

[τ] | М1 | М2 | М3 | М4 |
30 МПа | 160 Нм | 50 Нм | 80 Нм | 30 Нм |
(Ответ: диаметр вала d из условия прочности должен быть не менее 30 мм.)
Задача №7
Определите силу F, необходимую для продавливания круглым пуансоном диаметром a отверстия в листе металла толщиной δ. Предел прочности листового металла на срез: [τ] = 360 МПа.
Толщина листа металла δ | Диаметр пробойника а |
0,5 мм | 10 мм |
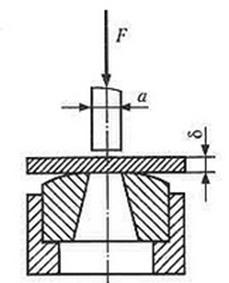
(Ответ: F ≥ Аср × [τ] ≥ δ × π × а × [τ] ≥ 0,0005 × 3,14 × 0,01× 360×106 ≥ 5652 Н,
здесь Аср – площадь цилиндрической поверхности, по которой осуществляется срез)
Задача №8
Брус постоянного сечения опирается на две опоры, одна из которых шарнирная, вторая – угловая (ребро). В середине бруса приложена поперечная изгибающая сила F = 200 Н.
Построить эпюру изгибающих моментов и показать наиболее нагруженное сечение бруса.
Вес бруса не учитывать.
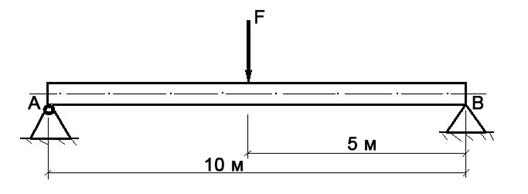
Решение задачи:
1. Исходя из того, что реакция угловой опоры направлена по нормали к оси бруса, составляем уравнение равновесия относительно опоры А (из условия равновесия - сумма моментов отностельно любой точки бруса равна нулю) и определяем реакцию опоры В:
10 RВ – 5 F = 0 => RВ =5 F/ 10 = 100 Н;
2. Строим эпюру изгибающих моментов, начиная от опоры В.
Наиболее нагруженное сечение бруса (изгибающий момент - 500 Нм) находится в его середине.

Задача №9
Брус постоянного сечения опирается на две опоры, одна из которых угловая (ребро), вторая – шарнирная. Брус нагружен изгибающим моментом Ми = 160 Нм.
Построить эпюру изгибающих моментов и показать наиболее нагруженное сечение бруса.
Вес бруса не учитывать.
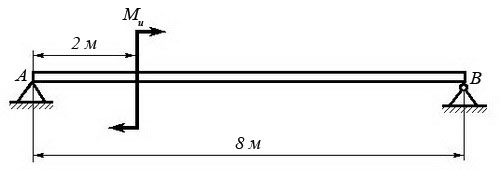
Решение задачи:
1. Исходя из того, что реакция угловой опоры направлена по нормали к оси бруса, составляем уравнение равновесия относительно опоры В (из условия равновесия - сумма моментов отностельно любой точки бруса равна нулю) и определяем реакцию опоры А:
8 RА – Ми = 0 => RА = Ми / 8 = 20 Н;
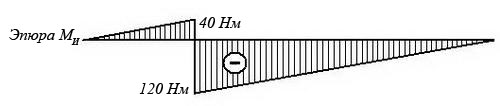
2. Строим эпюру изгибающих моментов, начиная от опоры А.
Наиболее нагруженное сечение бруса (изгибающий момент - 120 Нм) находится рядом с сечением, в котором приложен изгибающий моментМи (со стороны опоры В)
Задача №10:
Построить эпюру изгибающих моментов и выполнить расчет квадратного бруса на прочность, при условии, что предельно допустимое нормальное напряжение при изгибе: [σ] ≤ 100 МПа.
Вес бруса не учитывать.
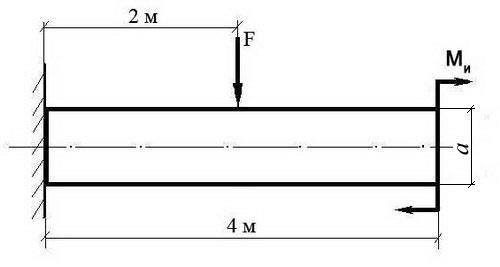
F | Ми | a |
100 Н | 100 Н/м | 0,1 м |
Задача №11
Построить эпюру изгибающих моментов и выполнить расчет бруса на прочность, при условии, что предельно допустимое нормальное напряжение при изгибе: [σ] ≤ 100 МПа. Вес бруса не учитывать.
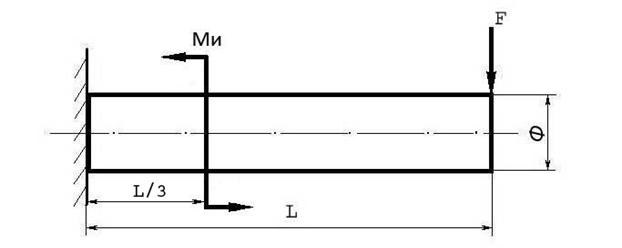
Изгибающий момент Ми | Поперечная сила F | Длина бруса L | Диаметр бруса Ф |
25 Нм | 250 Н | 12 м | 8 см |
Задача №12
Построить эпюру изгибающих моментов и выполнить расчет круглого бруса на прочность, при условии, что предельно допустимое нормальное напряжение при изгибе: [σ] ≤ 100 МПа.

Поперечная сила F | Распределенная нагрузка q | Диаметр бруса d |
100 Н | 20 Н/м | 10 см |
Задача №13

|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 10 |





