2. Худяков и др. Технология вторичных цветных металлов. М.: Металлургия, 1981, 280 с.
3. Купряков тяжелых цветных металлов из лома и отходов. Харьков: Основа, 1992. 400 с.
4. Периодические издание: Горный журнал, Цветные металлы, Ўзбекистон кончилик хабарномаси, Металлы Евразии, Рынок вторичных металлов.
Практическая работа №5.
Расчет шихты с учетом стоимости металлов,
входящих в состав сплавов.
(4 часа)
Цель работы: Ознакомить студентов с расчетами шихты с учетом стоимости металлов, входящих в состав сплавов.
Нередки случаи, когда предприятия вторичной цветной металлургии производят сплавы, сложные по химическому составу. При их получении основной статьей цеховой себестоимости является стоимость металлов, входящих в состав сплавов. Так, для сплава ЛЖМц 59-1-1 относительная стоимость металлов составляет 97,2 %, сплава ЛМц 58-2 95,23 %, сплава БрА7 95,29 % и т. д.
Сплавы можно получить из первичных металлов. В этом случае они будут иметь высокую себестоимость. Качество их будет отвечать самым высоким требованиям, так как первичные металлы на предприятиях первичной металлургии рафинируют и содержанке примесей в них незначительно. Но в состав шихты могут входить заранее приготовленные лигатуры (свинцово-кальциевая, медно-бериллиевая и др.), вторичные сплавы (медно-оловянные), а также лом и отходы. В этом случае себестоимость сплава может быть существенно снижена, но при этом может быть, и понижено его качество.
Для того, чтобы правильно составить шихту с целью получения относительно дешевого сплава, отвечающего техническим условиям, нужно правильно с шихтовать имеющиеся на предприятии первичные и вторичные металлы (сплавы) с учетом не только стоимости получаемого сплава, но и тех физико-химических изменений, которые составляющие шихты будут претерпевать в процессе его получения в металлургическом агрегате. Таким образом, перед металлургами возникает сложная комплексная задача, которая может быть решена методами линейного программирования. В этом случае задача сводится к оптимизации расхода шихтовых компонентов с учетом корректирующих добавок. При этом имеется ввиду расход не только металлов, но и флюсов.
Для оценки снижения затрат на шихту наиболее выгодным критерием оптимизации является ее стоимость. Для правильного использования этого параметра нужно выбрать вариант оптимизации. Он может быть многостадийным и одностадийным (рис. 2). Исходя из схемы многостадийного варианта, сначала определяют стоимость расчетного состава шихты F1 (параметр конечного состояния стадии r1,), затем F2 - затраты на дозирование отдельных составляющих шихты для корректировки первоначального расчета. Выходным параметром в этом случае является r2.
Приготовленную шихту загружают в металлургический агрегат. Затраты на этой стадии F3 складываются из энергетических затрат, затрат на огнеупоры, флюсы и т. д. Параметром стадии является r3.
После получения жидкого сплава и наведения флюса производят его корректировку. Большое внимание корректировке уделяется при наличии в сплаве металлов с повышенной упругостью пара при высоких температурах (цинк, кадмий, сурьма и т. д.). Затраты на эту стадию относительно невелики (F4). Параметр стадии r4.
Последней стадией является доводка сплава путем его рафинирования и введения модифицирующих добавок. Затраты на стадию - F5, параметр стадии г5. Затраты на стадию так же невелики, как и на F3, но она является наиболее ответственной из всех пяти стадий, так как готовый сплав должен отвечать требованиям стандарта.
Бывают случаи, когда предприятие должно получить сплав, отвечающий определенным требованиям. В практике часто бытует термин 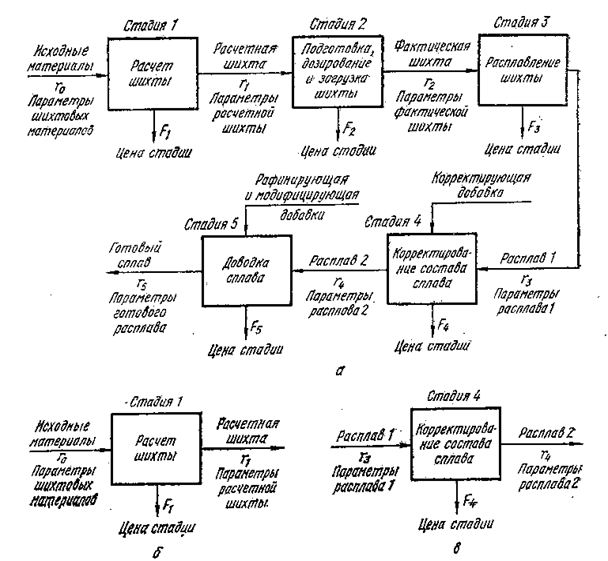 «приготовить сплав с заранее заданными свойствами».
«приготовить сплав с заранее заданными свойствами».
Рис. 2. Схема многостадийного (а) и одностадийных (б, в) вариантов оптимизации технологии приготовления сплавов
Общие затраты по рассмотренной пятистадиальной схеме (стадий может быть значительно больше) составят:
F = F1 + F2 + F3 + F4 + F5. (5-1)
Максимальная экономия получится только в том случае, если каждая стадия будет сопровождаться минимальными затратами:
MinF = minF1 + minF2 + minF3 + minF4 + minF5. (5-2)
Функция F, по которой производится оптимизация, называется целевой. Строго говоря, она не является линейной, так как ряд параметров (производительность печи, угар металла и т. д.) имеют нелинейную зависимость (в этом случае правильнее применить метод динамического программирования).
На первой стадии затраты равны:
F1 = C1X1 + C2X2 + C3X3 + C4X4 + C5X5 = ![]() CjXj, (5-3)
CjXj, (5-3)
где, Сj - цена единицы j-той составляющей шихты, сум/т;
Xj - расход j-той составляющей шихты в абсолютных или относительных единицах.
Общие затраты на шихтовые компоненты составят:
Fm = 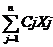 +
+ ![]() 4 +
4 + ![]() 5, (5-4)
5, (5-4)
где, Xj4, Xj5 - расход j-той составляющих шихты на стадии 4 и 5 (см. рис. 1).
Максимальное снижение расхода материала при его минимальном расходе па всех трех стадиях схемы равно:
minFm = minFm1 + minFm4 + minFm5 (5-5)
Величина minFм4 - незначительна по сравнению с Fм1, Fm5, как правило, постоянна, поэтому определение минимальных затрат металла на получение сплава сводится к решению задачи minFm1 = min ![]() CjXj, т. е. сводится к одностадийной схеме.
CjXj, т. е. сводится к одностадийной схеме.
От расхода металлов, т. е. правильности расчета первичной шихты, будет зависеть и стоимость получаемого сплава.
Расчет шихты следует разделить на три этапа:
1) определение регламентирующего химического состава сплава;
2) определение расчетного состава сплава с учетом имеющихся шихтовых материалов, которые будут использованы при плавке;
3) составление расчетных уравнений и их решение.
Уравнения должны предусматривать баланс по всем расчетным элементам, поступающим с шихтовыми материалами. В результате их решения получается оптимальное соотношение между составляющими шихты, которое при выбранном способе плавки обеспечивает заданный состав сплава.
Следует иметь в виду, что расчетный химический состав сплава должен отличаться от состава, регламентируемого стандартам, так как он должен учитывать возможные погрешности дозировки отдельных составляющих шихты, колебания в составе исходных материалов, угар и пригар металла и т. д., т. е. должно быть соблюдено условие
![]() , (5-6)
, (5-6)
где, Энiж и Эвiж - нижний и верхний расчетные допустимые содержания элемента Эi в сплаве.
В свою очередь
![]() ;
; ![]() (5-7)
(5-7)
где, ΔЭi - оптимальное содержание элемента Эi в сплаве по указанным выше причинам, %.
После решения первых двух позиций, предусмотренных расчетом шихты, приступают к составлению расчетных уравнений. Они обычно представляют собой систему равенств и неравенств. Так,
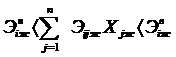 (5-8)
(5-8)
где, Эijж - количество расчетного элемента Эi усваиваемое жидким металлом из j-той составляющей шихты, %
или 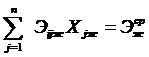 ;
;
q ≤ Xiж ≤ p (или Xiж = h), (5-9)
где, h, р, q - допустимые доли составляющих (лома, отходов, лигатуры) в формировании жидкого сплава;
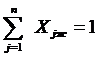 . (5-10)
. (5-10)
В соотношении типа (8) выражены ограничения по всем расчетным элементам; выражение (9) – технологические ограничения; (10) – балансовое уравнение по выходу жидкого металла. Все приведенные уравнения имеют величину Хjж, характеризующую j-тую долю составляющей в готовом сплаве 0 ≤ Хj ≤ 1. дл составления шихты удобнее иметь j-тую составляющую в шихту Хjш. Связь между этими величинами может быть представлена следующим равенством:
Хjш = Хjж / Кj, (5-11)
где, Кj – коэффициент усвоения или выход жидкого металла из j-той составляющей шихты; 0 ≤ Кj ≤ 1.
Так как Эijж = ЭijжКЭij, то с учетом равенства (11) расчетные уравнения (8)-(10) можно записать следующим образом:
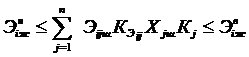 (5-12)
(5-12)
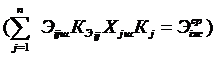 (5-13)
(5-13)
q ≤ Хjш Кj ≤ р; (5-14)
Хjш Кj = h; 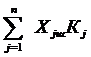 =1/ (5-15)
=1/ (5-15)
Если использовать среднее значение угара металлов, входящих в состав сплава, получится другая система балансовых уравнений:
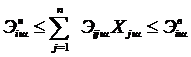 или
или 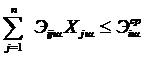 ; (5-16)
; (5-16)
qш ≤ Хjш ≤ рш; (5-17)
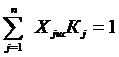 или
или 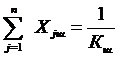 (5-18)
(5-18)
Данные уравнения могут быть использованы для расчета оптимального состава шихты с помощью ЭВМ с введением стандартных программ решения системы линейных алгебраических уравнений (СПАУ).
Контрольные вопросы.
1. Что является основной статьей цеховой себестоимости?
2. Рассчитайте шихту с учетом стоимости металлов, входящих в состав сплавов?
3. Как правильно составить шихту?
4. Каким образом можно максимально экономить энергию?
5. Сколько схем существует многостадийного приготовления сплавов?
Литература

|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 10 |




