Максимальная податливость технологической системы:
Wmax= 24 + 20 = 44 мкм/кН.
На предшествующей операции (черновом точении) заготовка обработана с допуском по JT13, т.е. возможное колебание припуска составляет JT13/2, что для диаметра 32,8 мм составит 0,4/2 = 0,2 мм.[5, табл. 32, гл.4] С учетом этого минимальное и максимальное значение глубины резания составят:
tmin = 0,5 мм; tmax = 0,5 + 0,2 = 0,7 мм
С учетом этого определяем наибольшую Py max и наименьшую Ру min нормальные составляющие усилия резания:
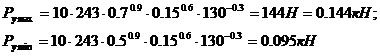
Тогда погрешность обрабатываемого размера вследствие упругих деформаций составит:
Dу=44×0,144-20×0,095=8,2 мкм
в). Определим погрешность Dст, вызванную геометрическими неточностями станка.
Согласно справочным данным [5, табл. 23, гл.1] для токарных станков нормальной точности при наибольшем диаметре обрабатываемой поверхности до 250 мм постоянство диаметра образцов в продольном сечении составляет С = 20 мкм при длине образцов L = 300 мм. С учетом того, что длина второй ступени 50 мм, получаем значение данной погрешности:
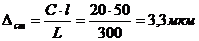
г). В предположении, что настройка резца на выполняемый размер производится по эталону с контролем положения резца с помощью металлического щупа, находим в справочнике погрешность регулирования положения резца Dр=10 мкм [5, табл. 26, гл.1] и погрешность измерения Dизм=20 мкм (для d2=35h10) [5, табл. 27, гл.1]. С учетом этого рассчитываем погрешность настройки:
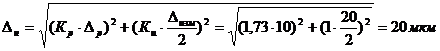
Кр = 1,73 и Ки= 1,0 — коэффициенты, учитывающие отклонения законов распределения величин Dр и Dизм от нормального.
д). Определим погрешность температурных деформаций технологической системы, приняв их равными 15% от суммы остальных погрешностей:
Dт=0,15(28 + 8,2+3,3 + 20) =9 мкм.
е). Определим суммарную погрешность обработки:
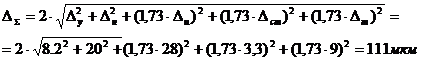
ж). Сделаем выводы. Суммарная погрешность превышает заданную величину допуска для d= 30 мм (Td= 84 мкм). В случае, когда чистовое точение является операцией, предшествующей дальнейшему шлифованию, превышением поля рассеяния в сравнении с полем допуска операционного размера чистового точения можно пренебречь, так как это превышение вызовет только колебание припуска на шлифование. Если же операция чистового точения является окончательной, обязательно требуется выполнение условия работы без брака.
Анализ элементарных погрешностей показывает, что наиболее действенным мероприятием для уменьшения суммарной погрешности размера является снижение погрешности от размерного износа резца. Этого можно достигнуть:
1) применением более износостойкого твердого сплава (например, вместо Т15К6 применить сплав Т30К4, имеющий почти в 2 раза меньший относительный износ) или соответствующим снижением режимов резания при использовании сплаваТ15К6;
2) уменьшением размера партии деталей, обрабатываемых за межнастроечный период (сокращение длины пути резания);
3) использованием автоподналадчиков, позволяющих периодически или непрерывно корректировать положение вершины резца при его износе.
Построение доверительных интервалов, проверка статистических гипотез.
По результатам измерения диаметров валов, обработанных в одинаковых условиях на двух токарных полуавтоматах, требуется (при доверительной вероятности 0,95) определить:
а) правильность настройки первого станка (станок настроен на диаметр Dн) – задача №1;
б) одинаковы ли станки по точности – задача №2;
в) различаются ли настроечные размеры станков – задача №3.
Таблица 3
N вар. | Ста-нок | Значения диаметров валов, мм | Dн, мм |
1 | 1 | 50,08; 50,15; 50,19; 50,07; 49,98; 50,06; 50,24; 49,98; 49,97; 50,15 | 50 |
2 | 50,02; 49,79; 50,32; 49,72; 49,64; 50,00; 50,40; |
| |
2 | 1 | 45,19; 45,05; 45,02; 45,16; 45,27; 45,00; 45,01; 45,18; 45,06 | 45 |
| 2 | 45,00; 45,29; 45,22; 45,54; 44,68; 45,24 |
|
3 | 1 | 54,99; 55,05; 55,01; 55,02; 54,98; 54,96; 54,87; 55,03 | 55 |
2 | 54,79; 54,95; 54,77; 54,61; 55,21; 54,61; 54,60 |
| |
4 | 1 | 42,83; 42,70; 43,35; 42,56; 43,12; 43,27; 43,51 | 43 |
2 | 42,70; 42,74; 42,88; 42,79; 43,00; 42,82; 42,78; 42,93; 42,86 |
| |
5 | 1 | 28,05; 27,81; 27,95; 28,13; 28,12; 28,11; 27,90; 27,91; 27,88; 28,01 | 28 |
2 | 27,96; 27,91; 27,68; 27,72; 28,05; 27,66 |
| |
6 | 1 | 31,97; 31,99; 31,95; 32,21; 32,13; 31,94; 32,22; 32,18; 31,92 | 32 |
2 | 31,96; 31,90; 31,85; 31,77; 32,26; 31,87; 31,98 |
| |
7 | 1 | 51,79; 52,62; 52,03; 51,87; 51,84; 52,17; 52,32 | 52 |
2 | 51,88; 51,82; 51,99; 51,96; 52,12; 51,62; 51,80; 51,74 |
| |
8 | 1 | 43,59; 43,60; 43,81; 43,77; 43,96; 43,85 | 44 |
2 | 44,00; 44,13; 44,26; 44,07; 43,98; 44,11; 44,23; 44,09; 44,08 |
| |
9 | 1 | 27,90; 27,92; 28,04; 27,99; 28,07; 27,92; 27,98; 27,97 | 28 |
2 | 28,24; 28,16; 28,23; 28,12; 28,13; 28,36; 28,16 |
| |
10 | 1 | 32,46; 32,33; 32,20; 32,48; 32,02; 31,82 | 32 |
2 | 31,99; 31,68; 32,05; 32,06; 32,01; 31,88; 31,83; 32,01 |
|
Порядок решения задачи №1.
Для решения задачи необходимо построить доверительный интервал для генерального среднего по следующей методике.
1. Определить выборочное среднее по формуле:
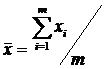 , (1)
, (1)
где xi - текущее значение случайной величины в выборке; m - объем выборки.
2. Определить выборочную дисперсию по формуле:
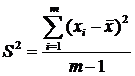 (2)
(2)
3. Рассчитать доверительный интервал:
![]() , (3)
, (3)
где Y, - генеральное среднее; ![]() , S2 - выборочные среднее и дисперсия; m – объем выборки; t - табличное значение критерия Стъюдента.
, S2 - выборочные среднее и дисперсия; m – объем выборки; t - табличное значение критерия Стъюдента.
Табличное значение критерия выбирается в зависимости от числа степеней свободы f=m-1 и принятой доверительной вероятности p из таблиц.
4. Проанализировать, попадает ли в доверительный интервал величина настроечного размера. Если она попадает в интервал, то с принятой доверительной вероятностью можно считать, что станок настроен правильно, и наоборот.
Порядок решения задачи №2.
Для решения задачи следует проверить гипотезу о равенстве двух дисперсий в следующей последовательности:
1. Определить выборочные средние по выборкам деталей, обработанных на двух станках по формуле 1.
2. Определить выборочные дисперсии по формуле 2.
3. Вычислить наблюдаемое значение критерия Фишера по формуле:
Fн=S12/S22 ,
Необходимо помнить, что в числитель всегда ставится большая дисперсия независимо от порядка их нумерации.
4. Найти в таблице критическое значение критерия Фишера Fкр для доверительной вероятности 0,95 и соответствующих числах степеней свободы обоих дисперсий f1=(m1-1) и f2=(m2-1).
5. Сделать вывод на основании сравнения наблюдаемого и критического значений критериев. Если Fн£Fкр, то дисперсии можно считать однородными, а это означает одинаковую точность партий деталей, и, соответственно, одинаковый уровень точности станков. В противном случае делается противоположный вывод.
Порядок решения задачи №3.
Для решения третьей задачи необходимо проверить гипотезу о равенстве средних значений в следующей последовательности:
1. Определить выборочные средние по выборкам деталей, обработанных на двух станках, по формуле 1.
2. Определить выборочные дисперсии по формуле 2.
3. Вычислить наблюдаемое значение критерия Стъюдента по формуле: 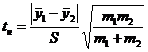 , (5)
, (5)
где S2 - объединенная оценка дисперсии генеральных совокупностей, определяемая по формуле:

|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 |




