6 Получение ММ процессов методом корреляционного анализа
Основные понятия теории систем случайных величин (ССВ). Нормальный закон распределения (ССВ). Корреляционное уравнение, коэффициент корреляции. Применение теории корреляции к задачам технологии машиностроения: установление связи между точностными характеристиками смежных операций ТП, анализ точности работы поточных линий.
Вопросы для самопроверки:
Закон распределения системы двух случайных величин. Условный закон распределения. Зависимые и независимые случайные величины. Стохастическая зависимость. Числовые характеристики системы случайных величин. Корреляционный момент, коэффициент корреляции. Нормальный закон распределения системы случайных величин. Корреляционное уравнение. Обоснование для применения корреляционного анализа при установлении связей между точностными характеристиками смежных технологических операций. Расчет выборочного коэффициента корреляции и параметров корреляционного уравнения. Переход от корреляционного уравнения к зависимости между погрешностями заготовки и детали.
7 Математическое моделирование в задачах оптимизации
Метод крутого восхождения при оптимизации технологических процессов. Требования к регрессионной модели. Расчет шагов при реализации метода. Стратегия последовательного приближения к области оптимума. Исследование области оптимума, представленной моделью второго порядка. Последовательное симплекс-планирование. Линейное программирование: общая постановка задачи. Линейное программирование в технологии машиностроения: задача об оптимальном составе ОТК, задача об использовании сырья, задача об использовании оборудования. Графическое решение задачи линейного программирования. Оптимизация режимов обработки резанием методом линейного программирования. Решение задачи в среде EXCEL.
Вопросы для самопроверки:
Понятие о методе крутого восхождения: градиент функции отклика, связь градиента с коэффициентами регрессионной модели. Реализация метода: расчет шагов движения по факторам, выполнение мысленных и реальных опытов, стратегия принятия решений. Исследование области оптимума, представленной моделью второго порядка: каноническое преобразование модели. Принятие решение о нахождении оптимума на основании коэффициентов модели, представленной в канонической форме. Сущность симплексного метода оптимизации. Симплексы для двух, трех и более факторов. Регулярный и нерегулярный симплекс. Построение матрицы исходного симплекса. Стратегия движения к области оптимума. Постановка задачи математического программирования. Целевая функция, функции ограничений. Область допустимых решений. Линейное программирование. Задача об определении оптимального состава отдела предприятия. Задача об оптимальном использовании сырья. Задача об оптимальном использовании оборудования. Графическое решение задачи линейного программирования. Решение задачи линейного программирования в среде EXCEL. Оптимизация режимов обработки резанием методом линейного программирования: выбор целевой функции, методика построения технических ограничений.
3. КОНТРОЛЬНАЯ РАБОТА ДЛЯ СТУДЕНТОВ
ЗАОЧНОЙ ФОРМЫ ОБУЧЕНИЯ.
Контрольная работа включает в себя три части. Ниже приведены варианты заданий и примеры их выполнения.
Расчет суммарной погрешности обработки детали на станке.
Ступени d1, d2, и d3 вала (табл.2) обрабатываются чистовым точением в центрах гидрокопировального станка модели 1Н713 с допуском IT10. Заготовки вала из стали 45 на предшествующей операции обработаны черновым точением по IT13. Обработка ведется резцом с пластиной из твердого сплава Т15К6 с параметрами: j= 45°, g=0°, l=0°; Требуется: определить элементарные погрешности и суммарную погрешность обработки ступени d2; сделать выводы о соответствии погрешности операции требуемым показателям точности, в случае несоответствия предложить мероприятия по уменьшению суммарной погрешности.
Таблица 2
Вари-ант | Размеры, мм | Предел проч-ности матери-ала детали, МПа | Миним. припуск на обработку, мм | Число заго-товок в партии N, шт. | Скорость резания, м/мин | Подача, мм/об | |||||
d1 | d2 | d3 | L1 | L2 | L3 | ||||||
0 | 40 | 30 | 25 | 100 | 150 | 225 | 750 | 0,5 | 30 | 130 | 0,15 |
1 | 100 | 85 | 75 | 100 | 250 | 325 | 1100 | 1,0 | 15 | 90 | 0,1 |
2 | 120 | 90 | 65 | 120 | 300 | 450 | 750 | 1,0 | 10 | 100 | 0,12 |
3 | 80 | 75 | 50 | 150 | 280 | 400 | 750 | 0,8 | 20 | 120 | 0,15 |
4 | 60 | 50 | 45 | 80 | 180 | 250 | 1100 | 0,6 | 25 | 110 | 0,2 |
5 | 50 | 45 | 35 | 100 | 150 | 200 | 750 | 0,6 | 30 | 140 | 0,16 |
6 | 85 | 100 | 75 | 100 | 250 | 425 | 900 | 1,0 | 20 | 90 | 0,1 |
7 | 90 | 120 | 65 | 120 | 300 | 450 | 1000 | 1,2 | 15 | 90 | 0,12 |
8 | 45 | 60 | 35 | 150 | 280 | 400 | 750 | 0,6 | 30 | 120 | 0,15 |
9 | 55 | 80 | 60 | 80 | 180 | 250 | 1100 | 0,6 | 25 | 130 | 0,2 |
10 | 45 | 50 | 30 | 100 | 150 | 200 | 900 | 0,5 | 40 | 120 | 0,16 |
11 | 30 | 45 | 25 | 100 | 150 | 225 | 750 | 0,5 | 35 | 140 | 0,15 |
Рассмотрим пример выполнения задачи для варианта №0.
а). Определим величину погрешности Dи (на радиус), вызванную размерным износом резца, по формуле:
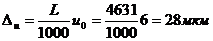
Здесь L – длина пути резания при обработке партии N деталей:
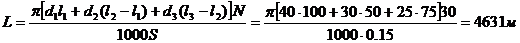
Для сплава Т15К6 относительный износ uо= 6 мкм/км [5, табл. 28, гл.1].
б). Определим колебание упругих отжатий системы Dу вследствие изменения силы Ру из-за непостоянства глубины резания и податливости системы при обработке по формуле:
где 
, 
— наибольшая и наименьшая податливость системы мкм/кН.
, 
— наибольшее и наименьшее значения составляющей силы резания, совпадающей с направлением выдерживаемого размера, кН.
Для станка 1Н713 нормальной точности наибольшее и наименьшее допустимые перемещения продольного суппорта под нагрузкой 16 кН составляют соответственно 450 и 320 мкм [5, табл. 11, гл.1]. При установке вала в центрах минимальная податливость системы будет возможна при положении резца в конце обработки, т.е. у передней бабки станка. Исходя из этого можно принять Wmin = 320/16 = 20 мкм/кН. Приближенно можно считать, что максимальную податливость система имеет при расположении резца посередине вала, когда его прогиб под действием усилия Py достигает наибольшей величины. Поэтому
где 
- наибольшая податливость станка (=(320+ 450)/(2 *16) = 24 мкм/кН);
— наибольшая податливость заготовки.
Определяем наибольшую податливость заготовки (мкм/кН) по формуле:
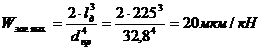
где lд - длина вала; dnр — приведенный диаметр вала, определяемый для случая одностороннего изменения диаметров ступеней по формуле:
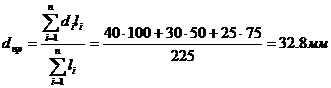
Для валов с двусторонним уменьшением диаметров ступеней приведенный диаметр определяется по формуле:
|
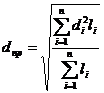
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 |
