где Nc и Nv – некоторые постоянные, mn и mp – эффективные массы для электрона и дырки соответственно.
N(E) вблизи зон проводимости и валентной имеет параболический вид (рис. 5.3). На рис. 5.3 площадь заштрихованных областей пропорциональна числу уровней в интервале энергий dE при единичном объеме.

Рис. 5.3. Распределение плотности
вероятности уровней в зоне проводимости
и валентной в зависимости от энергии
Число электронов в зоне проводимости с энергией от E до E + dE в единице объема при E >> Ef будет
dn = N(Е).Fn(E).dE. (5.8)
Число электронов во всей зоне проводимости, приходящееся на единицу объема, равно
Ґ
n = ò N(Е).Fn(E).dE, (5.9)
Еc
а число дырок в валентной зоне на единицу объема
Еv
p = ò N(Е).Fp(E).dE. (5.10)
0
Подставим (5.6) и (5.7) в (5.9) и (5.10)
Ґ
n = (4p / h3)(2mn)3 / 2ò(E – Ec)1 / 2.[1 + exp[(Е – Еf) / kT]–1.dE,
Еc
и выполнив интегрирование, получим
n = Nc.exp[– (Еc– Еf) / kT], (5.11)
где Nc = 2(2pmnkT / h2)3 / 2. Аналогично
p = Nv.exp[ – (Еf – Еv) / kT], (5.12)
где Nv = 2(2pmpkT / h2)3 / 2.
В уравнении (5.11) и (5.12) Nc и Nv характеризуют эффективную плотность квантовых состояний в зоне проводимости и валентной зоне соответственно. Они равны между собой, если равны соответствующие эффективные массы mn и mp.
Если положить, что mn = mp = mo, то
Nc = Nv = 2(2pmokT / h2)3 / 2 = 4,82.1015.T3 / 2 см–3. (5.13)
Для кремния mn = 0,26.mo и mp = 0,49.mo, поэтому Nc = = 6,36.1014.T3 / 2 см–3, Nv = 1,65.1015.T3 / 2 см–3. Используя графическое изображение F(E) и N(E), можно определить концентрацию носителей зарядов (рис. 5.4) согласно выражениям (5.9) и (5.10).

Рис. 5.4
Можно показать, что произведение n. p является функцией температуры и ширины запрещенной зоны (Еc – Ev) = Eg
n.p = Nc.Nv.exp[ – (Е c– Еv) / kT] = Nc.Nv.exp(Eg / kT). (5.14)
Ширина запрещенной зоны зависит от температуры, которая дается эмпирической формулой
Eg(T) = Eog – aT, (5.15)
где a = 2,8.10–4 эВ / К – температурный коэффициент.
Как видно из (5.14) и (5.15), правая часть уравнения (5.14) зависит только от Т и Еg и не зависит от n и p. Следовательно (5.14) справедливо как для собственных, так и для примесных полупроводников. Для собственных полупроводников n = p = ni, поэтому n. p = ni2 = pi2 – уравнение полупроводников.
Рассмотрим отношение p / n
p / n = (Nv / Nc).exp[(Ec + Ev – 2Ef) / kT], (5.16)
из которого следует
Еf = 0,5(Еc + Еv) – 0,5.kT.ln(p / n) – 0,75.kT.ln(mn / mp). (5.17)
Так как для собственного полупроводника ln(p / n) = 0, то при mp = mn
Ef = 0,5(Ec– Ev) (5.18)
Таким образом, мы получили подтверждение того, что уровень Ферми для собственного полупроводника расположен в середине запрещенной зоны.
Функция распределения Ферми – Дирака справедлива и для примесных невырожденных полупроводников. Поскольку в полупроводнике n-типа часть электронов поступает в зону проводимости не за счет образования дырок в валентной зоне, а из донорных уровней примеси, то вероятность появления электрона в зоне проводимости выше, чем вероятность появления дырки в валентной зоне. Это возможно только в том случае, если уровень Ферми будет смещен в сторону зоны проводимости и чем выше концентрация донорной примеси, тем больше это смещение. В примесном полупроводнике p-типа наоборот, смещение уровня Ферми происходит в сторону валентной зоны. Зонная структура примесных полупроводников n-типа и p-типа в сочетании с графическим представлением функции распределения Ферми – Дирака и плотности энергетических состояний в валентной зоне и зоне проводимости представлена на рис. 5.5.
Из приведенных графиков рис. 5.5 видно, что в примесном полупроводнике n-типа преобладает электронная проводимость, главным образом, за счет донорной примеси, которая уже при комнатной температуре полностью ионизована. Электроны в данном случае считаются основными носителями, которых значительно больше, чем неосновных (дырок), что согласуется с аналитическим выражением для концентрации электронов в примесном полупроводнике. В примесном полупроводнике p-типа преобладает дырочная проводимость.
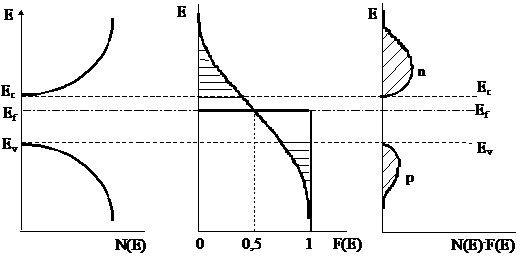

Рис. 5.5
Если полупроводник одновременно легирован донорной и акцепторной примесью, то тип проводимости будет определяться соотношением концентраций соответствующих примесей.
Как указывалось выше, в сильно легированном полупроводнике наступает вырождение. В этом случае уровень Ферми в полупроводнике n-типа близок ко дну зоны проводимости или даже заходит в нее, а в полупроводнике p-типа соответственно приближается к потолку валентной зоны. В более строгом смысле вырожденный полупроводник характеризуется неравенством
Ec – Ef < 3kT. (5.19)
При повышении температуры уровень Ферми в примесных полупроводниках смещается к середине запрещенной зоны, т. к. собственная проводимость при этом возрастает и может превысить примесную.
5.3. Вырожденные полупроводники
Общепринятым критерием невырожденности полупроводника является значение функции Ферми – Дирака F << 1. Вырождение наступает при увеличении концентрации примеси. Определим ту предельную концентрацию, при которой полупроводник переходит в состояние вырождения. Для этого проанализируем уравнения (5.11) и (5.12), определяющие концентрацию носителей зарядов в невырожденных полупроводниках. При Ef = Ec, n = Nc и при Ef = Ev, p = Nv. Nc и Nv представляют собой максимально возможную концентрацию подвижных электронов и дырок в зоне проводимости и валентной зоне соответственно невырожденного полупроводника.
В вырожденном полупроводнике уровень Ферми может располагаться выше дна зоны проводимости и ниже потолка валентной зоны. Переход от невырожденного состояния в вырожденное может произойти при любой температуре по мере увеличения концентрации примеси. Предельная концентрация перехода от невырожденного состояния к вырожденному составляет N > 10–18 см–3.
6. КИНЕТИЧЕСКИЕ ЯВЛЕНИЯ
В ПОЛУПРОВОДНИКОВЫХ МИКРОСТРУКТУРАХ
Под кинетическими явлениями понимают процессы переноса зарядов (электронов дырок) в полупроводниках. Учитывая малые линейные размеры микроэлектронных структур, специфика переноса зарядов имеет ряд особенностей, как то: большие локальные напряженности электрического поля, большие градиенты концентрации носителей зарядов (резкие полупроводниковые переходы), взаимное влияние элементов ИС и др. Учесть все эти особенности весьма трудно, поэтому в качестве первого приближения используют аналитические выражения, полученные при l << L, где L – линейные размеры структуры, а l – длина свободного пробега электрона. Эти вопросы подробно изложены в [1, 9, 11].
На движение заряженных частиц влияют четыре основных фактора: температура, электрические и магнитные поля и градиент концентрации.
Тепловое движение частиц в силу его хаотичности обуславливает лишь рассеяние потока частиц, однако на направленное движение не влияет.
Рассмотрим процесс переноса электронов и дырок в условиях стационарной неравновесности при отсутствии магнитного поля. Перемещение зарядов под действием электрического поля называется дрейфом частиц, характеризующимся дрейфовой скоростью vnE = mnE – для электронов и vpE = mp.E – для дырок, где m – дрейфовая подвижность.
Плотность тока для электронов и дырок запишется
jnE = envnE = enmnE, jpE = epvpE = epmpE. (6.1)
Суммарная подвижность дрейфового тока равна
jnE + jpE =e(nmn + pmp)E = sE, (6.2)
где s – удельная электропроводность.
Дрейфовые скорости vnE и vpE направлены противоположно, однако плотности токов складываются, т. к. их сумма характеризует общую сумму переноса зарядов (рис. 6.1).
E vnE jnE
n –––––® ––––– –––––®
E vpE jpE
p –––––® –––––® –––––®
Рис. 6.1
При наличии градиента концентрации носителей зарядов возникает диффузионная составляющая плотности тока:
JnD = eDn(dn / dx), JpD = – eDp(dp / dx). (6.3)
Отрицательный знак означает тот факт, что вектор плотности диффузионного тока направлен в сторону, противоположную градиенту концентрации дырок (рис. 6.2).
dn / dx n JpD
n –––––® ––––– –––––®
dp / dx p JnD
p –––––® ––––– –––––
Рис. 6.2
Если явления дрейфа и диффузии наблюдаются одновременно, то в этом случае для одномерной модели можно записать следующие соотношения для плотности электронного и дырочного тока:
Jn = jnE + jnD = enmnE + eDn(dn / dx), (6.4)
jp = jpE + jpD = epmpE – eDp(dp / dx). (6.5)
Между явлениями дрейфа и диффузии существует некоторая связь, которая количественно определяется соотношением Альберта Эйнштейна [9].
6.1. Эффект Холла
Как известно, эффект Холла возникает в полупроводнике, находящемся в постоянном магнитном поле, индукция которого B перпендикулярна направлению протекающего через образец постоянного тока I. При этом в полупроводнике возникает электрическое поле (э. д. с. Холла), вектор напряженности которого Eх нормален плоскости B.I (рис. 6.3).
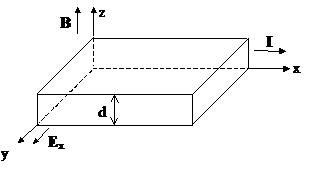
Рис. 6.3. Полупроводниковый образец,
в котором наблюдается эффект Холла
Этот эффект позволяет экспериментально определить тип электропроводности полупроводника, концентрацию носителей и их подвижность, используя выражение для э. д. с. Холла (Eх):
Ex = Rx.I.B / d, (6.6)
где Rx = Rxn = – An / ne – постоянная Холла для электронного полупроводника или Rx = Rxp = Ap / pe – для дырочного полупроводника (n и p – концентрация электронов и дырок соответственно), d – толщина образца, An и Ap – коэффициенты, величина которых зависит от образцов и изменяется в пределах от 0,5 до 2,0. В сильных магнитных полях для вырожденных полупроводников А = В = 1,0. Из формулы (6.6) видно, что э. д. с. Холла тем выше, чем тоньше образец полупроводника. С позиции микроэлектронных структур, в которых используются тонкие полупроводниковые слои, эффект Холла может существенно влиять на работу микроэлектронных изделий, подвергающихся воздействию сильных магнитных полей.
6.2. Генерация и рекомбинация носителей зарядов
Кроме дрейфа и диффузии, в полупроводниковых материалах может происходить генерация дополнительных носителей зарядов, а также их рекомбинация. Эти явления бывают двух типов – прямые (межзонные) и промежуточные (ступенчатые), обусловленные наличием промежуточных уровней (рис. 6.4).
__________ Ec __________ Ec
G ½ _ _ _¯_ _Ei
½ ¯R Ev ¯ Ev
Рис. 6.4
Кроме того, следует учитывать поверхностные явления, которые трактуются как уровни Тамма – Шокли, эквивалентные появлению в запрещенной зоне дополнительных уровней, центров рекомбинации. Наконец, неоднородное распределение носителей зарядов в полупроводнике создает внутренние локальные неоднородные электрические поля, которые тоже следует учитывать при определении плотности суммарного тока.
С учетом вышесказанного, генерация и рекомбинация носителей зарядов приводит к нарушению термодинамического равновесия, и прежние соотношения для концентрации электронов и дырок несправедливы. В этом случае, вместо уровня Ферми Еf, вводятся две величины Efn и Efp, и уравнения (5.11) и (5.12) примут вид
n = Nc.exp[ – (Еc – Еfn) / kT], (6.7)
p = Nv.exp[ – (Еfp – Еv) / kT], (6.8)
где Еfn и Еfp трактуются как квазиуровни Ферми для электронов и дырок соответственно.
Выполнив подстановки Yn = – Efn / e, Yp = – Efp / e, Y = – Ei / e, преобразуем формулы (6.7) и (6.8) к виду
n = ni. exp[(Y – Yn) / UT], (6.9)
p = ni. exp[(Yp – Y) / UT], (6.10)
где Yn и Yp – так называемые потенциалы Ферми, Y – электро-статический потенциал, UT = kT / e – температурный потенциал.
6.3. Явления переноса в динамически неравновесном состоянии;
уравнение непрерывности
С учетом явлений дрейфа и диффузии носителей зарядов, а также процессов генерации и рекомбинации, можно составить фундаментальные уравнения, описывающие изменения во времени избыточных носителей зарядов (электронов и дырок) в полупроводниковых материалах.
Идея, лежащая в основе вывода этих уравнений, базируется на том, что разность между числом входящих и выходящих носителей для некоторого объема равна изменению числа частиц в этом объеме.
¶n / ¶t = – dJn / dx + Gn – (n – no) / tn, (6.11)
¶p / ¶t = – dJp / dx + Gp – (p – po) / tp, (6.12)
где Jn и Jp – плотности потока электронов и дырок, Gn и Gp – коэффициенты генерации дополнительных носителей зарядов, (n – no) / tn и (p – po) / tp – коэффициенты рекомбинации для электронов и дырок соответственно, tn и tp – среднее время жизни, no и po – равновесные концентрации.
Выражая потоки заряженных частиц через токи, получим окончательное выражение для уравнений непрерывности
¶n / ¶t = Dn(¶2n / ¶x2) + mnEx(¶n. / ¶x) + Gn – (n – no) / tn, (6.13)
¶p / ¶t = – Dp(¶2p / ¶x2) + mpEx(¶p / ¶x) + Gp – (p – po) / tp. (6.14)

|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 10 11 12 |




