В настоящее время диоксид и нитрид кремния, благодаря технологичности их получения, являются наиболее распространенными диэлектриками в микроэлектронике.
Поликристаллический кремний также находит широкое применение в микроэлектронике. В зависимости от степени легирования он может быть использован в качестве затвора в МОП-структурах, для формирования интегральных резисторов, в виде источника диффузии при создании мелких p–n-переходов, при формировании проводящих дорожек и для создания ОМ-контактов.
В случае легирования кислородом с последующим температурным отжигом, поликристаллический кремний окисляется и в виде SiO2 используется как диэлектрик, хотя по параметрам уступает высокотемпературному окислу кремния.
3.4. Металлы в микроэлектронике
Металлы в микроэлектронике используются, главным образом, в процессе металлизации, т. е. при создании проводящих каналов, соединяющих отдельные элементы в единую интегральную схему, а также при создании омических контактов, обкладок конденсаторов, затворов в МОП структурах, в барьерах Шоттки, в фотошаблонах, внешних выводах, в качестве материала для корпусов интегральных схем и др.
К металлам, используемым в микроэлектронике, предъявляется ряд специфических требований, а именно: низкое удельное сопротивление, хорошая адгезия, технологичность (низкая температура плавления, удобство нанесения в виде пленки, возможность сварки с внешними выводами), экономичность (низкая стоимость), коррозионная стойкость и др.
На протяжении всего периода развития микроэлектроники наибольшее распространение в микроэлектронике получил алюминий, отвечающий перечисленным выше качествам и, главным образом, благодаря возможности термического распыления.
В последнее время, благодаря широкому внедрению магнетронного распыления материалов, широко используются силициды тугоплавких металлов (W, Mo, Ti, Ta и др.), которые, благодаря низкому удельному сопротивлению ( ниже 100 мкОм.см) и малому времени задержки при прохождении сигналов, вытеснили применяемый до этого легированный поликремний в затворных структурах МОП. Технология нанесения металлических пленок будет рассмотрена в последующих главах.
Кроме рассмотренных выше основных материалов, в микроэлектронике широко используются не менее важные вспомогательные материалы. Так, в литографии при создании рисунка интегральной схемы применяется большое количество позитивных и негативных фоторезистов. Для размерного жидкостного или вакуумно-плазменного травления защитных масок, а также для создания металлических межсоединений используется большой набор различных кислот, органических растворителей и газообразных веществ. Наконец, в гибридных интегральных схемах в качестве подложки используются специальные керамики, пасты и защитные лаки. Более подробно об этих материалах будет сказано в последующих разделах.
4. СТРУКТУРНЫЕ И ЭНЕРГЕТИЧЕСКИЕ МОДЕЛИ МАТЕРИАЛОВ МИКРОЭЛЕКТРОНИКИ
Физические процессы, протекающие в полупроводниках, удобно рассматривать с позиции соответствующей модели. Любая адекватная модель явления, несмотря на некоторое упрощение рассматриваемого объекта, позволяет объяснить его свойства, а в некоторых случаях и предсказать ранее неизвестные факты. Применительно к полупроводникам наибольшее распространение получили: модель ковалентной связи, модель энергетических зон, включая простую физическую и математическую модель Кронига-Пенни, в доступной форме изложенную в работах [9, 11].
4.1. Модель ковалентной связи
Не останавливаясь на аморфной и поликристаллической структурах твердых тел, более подробно рассмотрим монокристаллическую, используемую в производстве ИС. Отметим, что основную роль в процессе объединения атомов в кристалл, играют внешние электроны. В данном случае кроме ковалентной связи, при которой внешние, т. е. валентные электроны становятся общими для ближайших соседних атомов, различают ионную и металлическую связь.
При ионной связи соседние атомы как бы обмениваются электронами, в результате чего в структуре образуются разнополярные ионы. Примером может служить связь двух атомов 1 и 7 группы, например NaCl.
При металлической связи кристаллическая решетка «пропитана» электронным газом. Внешние электроны не связаны с конкретными атомами и свободно перемещаются в пределах данного металла.
В твердых телах (в том числе и в полупроводниках) с ковалентной связью атомы могут группироваться в различные формы кристаллической решетки: простую кубическую, в каждой вершине которой располагается один атом, принадлежащий одновременно восьми соседним элементарным ячейкам; кубическую объемно-центрированную, где, помимо атомов в вершинах кубов, имеется еще один атом в центре (Mo, W); кубическую гранецентрированную, у которой, кроме восьми атомов в вершинах куба, шесть атомов располагаются в центрах граней (Al); решетка типа алмаза, которая представляет собой две, вложенные друг в друга кубические гранецентрированные решетки, смещенные на расстояние четверти диагонали куба (C, Si, Ge), и решетка типа (GaAs), которая конструируется из решетки типа алмаза, где атомы Ga совпадают с узлами одной гранецентрированной решетки, а атомы As – с узлами другой. Более подробно с кристаллической структурой твердых тел можно познакомиться в специальной литературе.
Один из наиболее распространенных полупроводников – кремний (Si), является элементом четвертой группы и на верхней оболочке имеет четыре валентных электрона, обеспечивающих ковалентную связь, при которой каждый атом валентными электронами связан с четырьмя соседними атомами (рис. 4.1). При использовании более наглядной плоской модели Si каждая межатомная связь реализуется двумя общими электронами (рис. 4.2).
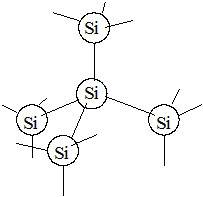
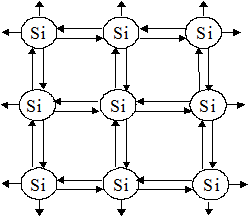
Рис. 4.1. Тетраэдрическое пространственное расположение атомов Si в кристаллической решетке | Рис. 4.2. Двумерная модель ковалентной связи атомов Si в кристаллической решетке |
Если удалить один из атомов кремния в решетке и заменить его на трех - или пятивалентный атом (бор или фосфор соответственно), то в первом случае одна из связей кремния не будет скомпенсирована (у бора всего три валентных электрона) и в полупроводнике образуется положительный заряд – дырка, характеризующая полупроводник р-типа. В случае пятивалентной примеси (фосфор) пятый валентный электрон окажется «лишним» и не будет связан с валентным электроном кремния. В итоге получим полупроводник n-типа с электронной проводимостью. Двумерные модели полупроводников p-типа и n-типа представлены на рис. 4.3.
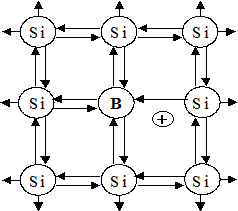
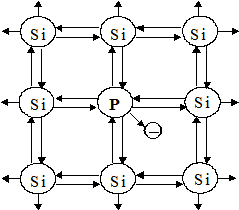
p n
Рис. 4.3. Двумерная модель кристаллической решетки Si
с примесными атомами p-типа и n-типа
Реальный монокристалл всегда имеет не скомпенсированные валентные связи на границе (поверхности), которые определяют его поверхностные свойства.
4.2. Модель энергетических зон
Модель энергетических зон в твердом теле вводится для того, чтобы связать между собой энергию и импульс носителей заряда в кристаллах. Она позволяет найти распределение электронов и дырок по энергиям в полупроводнике.
Рассмотрим вначале простую физическую модель энергетических зон [9].
Согласно квантовой механике электрон, входящий в состав атома, рассматривается как некая квазичастица, свойства которой описываются уравнением Шредингера (4.1)
С2Y(x, y, z) + (p82m / h2)[E – V(x, y, z)]Y(x, y, z) = 0, (4.1)
где С2 = (¶2/¶x2)+(¶2/¶y2)+(¶2/¶z2), Y(x, y, z) – волновая функция, Е – полная энергия электрона, V(x, y, z) – потенциальная энергия электрона.
Уравнение (4.1) имеет отличное от нуля решение только при некоторых дискретных значениях энергии Е, что соответствует некоторому квантовому состоянию. Этому состоянию отвечает определенное значение энергии Е и импульса (mv или ћk), иначе, можно утверждать, что электрон, входящий в состав свободного атома, характеризуется набором квантовых чисел и дискретных значений энергии. При этом говорят, что электроны в атоме занимают некоторые разрешенные уровни (s, p, d и т. д.).
Из-за большой концентрации атомов в твердом теле происходит расщепление каждого уровня и образование соответствующих зон аналогично, как происходит деформация резонансной кривой двух связанных колебательных контуров при сильной связи. Процесс расщепления энергетических уровней и образование энергетических зон можно продемонстрировать на примере атома углерода. В его структуре на k – оболочке с двумя подоболочками имеется два и шесть уровней соответственно. Первая оболочка с двумя уровнями заполнена. На второй из шести уровней заполнено только два, поэтому четыре уровня являются свободными. При сближении атомов, как это показано на рис. 4.4, происходит постепенное расщепление уровней. Расстояние X1 – соответствует состоянию свободного атома углерода. При сближении атомов до расстояния X2 образуются две зоны; при расстоянии X3 две зоны сливаются в одну, что соответствует состоянию графита. При дальнейшем сближении до X4 образуются три зоны, соответствующие структуре алмаза: внизу валентная зона (Ev), образованная четырьмя валентными электронами (два электрона на уровне 2s и два на уровне 2p), вверху – зона проводимости (Еc) с четырьмя свободными вакансиями и между ними запрещенная зона (Еg). Наличие запрещенной зоны характерно для всех полупроводников.

Рис. 4.4. Образование энергетических зон в атоме углерода
Зонная модель может быть представлена в упрощенном виде (рис. 4.5). Каждый атом углерода, входящий в состав кристалла, имеет четыре электрона в валентной зоне. Кроме того, каждому атому отведены четыре вакантных уровня в зоне проводимости.
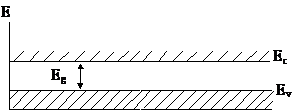
Рис. 4.5. Классическая энергетическая
зонная модель полупроводника
При нулевой температуре зона проводимости пуста, а валентная заполнена полностью и электропроводность при этом отсутствует. Если электрону сообщить энергию Е > Еg, то он может перейти в зону проводимости. При комнатной температуре (300 К) эта энергия, определяющая величину запрещенной зоны, составляет 1,12 эВ для Si, 0,72 эВ для Ge и 5,5 эВ для алмаза.
В зависимости от расположения зон и величины запрещенной зоны все твердые тела подразделяются на диэлектрики, полупроводники и металлы (рис. 4.6).
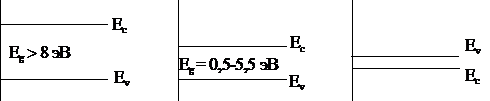
Диэлектрик Полупроводник Металл
Рис. 4.6. Энергетическая зонная модель для диэлектрика, полупроводника и металла
В диэлектрике тепловое возбуждение недостаточно для перевода электрона из Еv в Ec. В металлах из-за слабой связи электронов со своими атомами валентная зона и зона проводимости перекрываются. Промежуточное положение по ширине запрещенной зоны занимают полупроводники. Внешние электроны всегда находятся в зоне проводимости и под действием электрического поля могут перемещаться в направлении поля.
Следует иметь в виду, что описанная выше упрощенная модель является лишь наглядным графическим изображением, а энергетические зоны следует трактовать не как каналы, разрешенные для перемещения электронов и дырок, а лишь как совокупность энергетических уровней, характеризующих возможность состояния заряженных частиц.
В энергетических диаграммах ось энергии направлена вверх и так как заряд электрона отрицательный, то ее значения на оси численно равны электрическому потенциалу.
4.3. Математическая модель энергетических зон
(модель Кронига-Пенни)
Одной из наиболее простых и эффективных математических моделей зонной структуры полупроводников является модель Кронига-Пенни [9]. Она позволяет более точно определить энергетические зоны как простых, так и сложных полупроводников и получить сведения о квантово-механических свойствах электрона.
Согласно модели Кронига-Пенни (рис. 4.7), электрон, находящийся в периодической решетке (решетка Браве), при движении испытывает периодическое ускорение и замедление под действием электрического поля атома. Распределение потенциала для простоты расчета представлено в виде периодически чередующихся барьеров прямоугольной формы величиной Vo, предполагая, что кристалл является однородным и неограниченно протяженным.
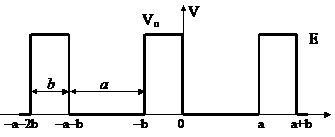
Рис. 4.7. Модель Кронига-Пенни:
a – ширина потенциальной ямы; b – ширина области с потенциалом Vo; а + b – постоянная решетки
Движение электрона вдоль такой решетки описывается волновой функцией Y(x), которая является решением уравнения Шредингера
d2Y(x) / dx2 + (2m / ћ)[E – V(x)]Y(x) =
Простейшим решением уравнения (4.2) является плоская волна с некоторым волновым числом, модулированная по амплитуде некоторой функцией, период которой совпадает с периодом кристаллической решетки. Такие решения называют функциями Блоха, которые после преобразования принимают вид:
[(b2 – a2) / 2ab].sh(bb).sin(aa) + ch(bb)cos(aa) = cos(kL) =
= cos(2np / N) при Е < Vo, (4.3)
– [(a2 + g2) / 2ag].sin(gb).sin(aa) + cos(gb).sin(aa) = cos(kL) =
= cos(2np / N) при Е > Vo, (4.4)
где a2 = 2mE / ћ2, b2 = 2m(Vo – E) / ћ2, b = ig, L = a + b, k = 2np / NL, Vo – высота потенциального барьера, E – полная энергия электрона.
Уравнение (4.3) и (4.4) являются математической моделью Кронига-Пенни.
Положив b ® 0, а V® Ґ, при этом Vb = соnst, и введя параметр
P = lim(b2ab / 2),
b® Ґ
b® 0
получим
(p / aL).sin(aL) + cos(aL) = cos(kL). (4.5)
Поскольку a2 = 2mE / ћ2, то уравнение (4.5) устанавливает связь между полной энергией электрона (Е) и волновым вектором (k). График этой зависимости представлен на рис. 4.8.
Таким образом модель Кронига-Пенни на основании решений уравнения Шредингера для кристаллической структуры твердого тела доказывает существование разрешенных и запрещенных зон в монокристалле полупроводника. График зависимости Е(k) на рис. 4.8 б получен при сдвиге соответствующих зон слева и справа на величину nL, что допустимо, т. к. функция периодическая.
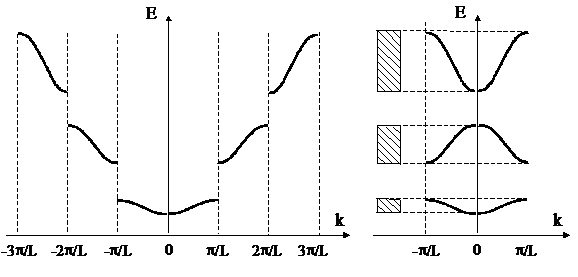 а б
а б
Рис. 4.8. Функция Е(k) в соответствии с моделью Кронига-Пенни (а). Зависимость Е(k), приведенной к первой зоне Брюллиоэна (б), разрешенные зоны заштрихованы
Ограничиваясь рассмотрением энергетических зон для валентных электронов, зонная структура будет иметь вид (рис. 4.9):

Рис. 4.9. Зонная структура простого полупроводника (Si) для валентных электронов
Нижняя часть энергетической диаграммы в обычных условиях для полупроводника (валентная зона – Ev), как правило, заполнена. Верхняя (зона проводимости – Ec) при Т = 0 К пуста. Между ними расположена запрещенная зона Eg = Ec – Ev. Для создания проводимости в полупроводнике необходимо перебросить электроны с валентной зоны в зону проводимости, сообщив им энергию Е > Еg. Отсутствие электрона в валентной зоне воспринимается как положительный заряд, равный заряду электрона (дырка). Движение электронов и дырок в полупроводнике характеризуется эффективной массой m*, которая отличается от массы покоя и различна для электронов и дырок:
m*n № m*p. (4.6)
4.4. Модель энергетических зон для примесных полупроводников
В собственном полупроводнике (без примесей) при Т = 0 К валентная зона полностью заполнена электронами, а зона проводимости свободна. Уровень Ферми при этом расположен посредине запрещенной зоны (рис. 4.10).
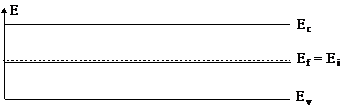
Рис. 4.10
При Т > 0 К полупроводник приобретает собственную проводимость за счет одновременной термогенерации электронно-дырочных пар. Если в полупроводник внести примесь, то в зависимости от ее валентности полупроводник приобретет электронную проводимость (в случае пятивалентной примеси – P или As) или дырочную (в случае трехвалентной примеси – B, Ga). Примесные атомы создают дополнительные уровни энергии, расположенные внутри запрещенной зоны: n-типа – вблизи дна зоны проводимости и p-типа – над потолком валентной зоны. Аналогично смещается и уровень Ферми.
Ширина запрещенной зоны зависит от температуры:
Eg = (Eс – Ev) – e(T).T, (4.7)
где e(T) = 3.10–4 В/K.
Положение уровня Ферми также зависит от температуры, смещаясь по мере ее увеличения к середине запрещенной зоны, так как увеличивается собственная проводимость.

а б
Рис. 4.11. Смещение уровня Ферми (Ef) в зависимости от температуры примесного полупроводника (а – n-типа и б – p-типа)
Положение уровня Ферми в примесных полупроводниках при низких температурах определяется формулой
Ef = (Ec – E d) / 2 + (kT / 2).ln(Nd / Nc), (4.8)
где Ed – энергетический уровень донорной примеси, Nd – концентрация донорных примесей, Nc – плотность состояний в зоне проводимости.
При Т = 0
Ef = (Ec – Ed) / 2. (4.9)
С повышением температуры примесная проводимость приближается к насыщению, а собственная монотонно увеличивается, и, как отмечалось выше, примесный полупроводник как бы превращается в собственный, а уровень Ферми смещается к середине запрещенной зоны.
5. СТАТИСТИКА НОСИТЕЛЕЙ ЗАРЯДОВ
В ПОЛУПРОВОДНИКОВЫХ МАТЕРИАЛАХ МИКРОЭЛЕКТРОНИКИ
5.1. Статистика Ферми – Дирака
Целью любой статистической теории является нахождение функции распределения частиц по определенному параметру, в частности, вероятности того, что в условиях термодинамического равновесия при заданной температуре некоторая частица занимает определенный энергетический уровень Е.
В зависимости от энергетического состояния рассматриваемого ансамбля частиц статистический подход к его описанию может быть различным. Например, если рассматриваются частицы в произвольном внешнем потенциальном силовом поле, то для описания их энергетического состояния применима функция распределения Больцмана [9]:
fБ(Е, Т) = C e–Е / kT, (5.1)
где С – некоторая постоянная, а k – постоянная Больцмана.
График этой функции имеет вид, представленный на рис. 5.1.
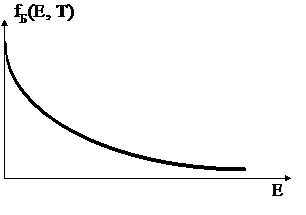
Рис. 5.1. Функция распределения Больцмана
Распределение неразличимых квантово-механических частиц, описываемых симметричными волновыми функциями, определяется статистикой Бозе – Эйнштейна (5.2). При этом считается, что число частиц, которые могут занимать один и тот же уровень, не ограничено.
fБЭ(Е, Т) = {1 – exp[(Е – Ев) / kT]}–1, (5.2)
где Ев – некоторая постоянная величина.
Распределение подвижных носителей зарядов по энергиям в кристалле собственного (беспримесного) полупроводника описывается квантово-механической функцией Ферми – Дирака. Следует иметь в виду, что речь идет о распределении электронов или дырок по энергиям в условиях термодинамического равновесия при фиксированной температуре. Статистика Ферми – Дирака применима к частицам, волновые функции которых антисимметричны и подчиняются запрету Паули (на одном и том же квантовом уровне не может находиться более одного электрона). Аналитически функция Ферми – Дирака для электронов записывается уравнением (5.3).
Fn(E, T) = {1 + exp[(Е – Еf) / kT]}–1, (5.3)
где Еf – уровень Ферми, физический смысл которого будет уточнен ниже.
При Е >> Еf функция Ферми – Дирака переходит в функцию Максвелла-Больцмана, что упрощает рассмотрение некоторых параметров полупроводниковых устройств.
Графически функция Ферми – Дирака в двух вариантах представлена на рис. 5.2.

Рис. 5.2. Функция Ферми – Дирака для электронов Fn(E) и дырок Fp(E)
Если в качестве параметра выбрать Т, то F(E) может принимать следующие значения:
1) T = 0, Fn(E) = 0 при E > Еf, Fn(Е) = 1 при Е < Ef;
2) Т > 0, Fn(E) ® 1 при Е ® 0, Fn(E) ® 0 при Е ® Ґ.
При любых температурах (Т = 0 и Т ¹ 0) F(E) = 0,5 при Е = Еf. Отсюда видно, что так называемый уровень Ферми (Еf) представляет собой тот энергетический уровень, вероятность заполнения которого при любой температуре составляет 0,5.
Функцию распределения для дырок Fp(Е) найдем из очевидного равенства
Fn(Е, Т) + Fp(Е, Т) = 1, (5.4)
откуда Fp(Е, Т) = 1 – Fn(Е, Т) = {1 + exp[(Еf – E) / kT]}–1. (5.5)
Если Е >> Еf, то F(E, Т) = C.exp(– E / kT), т. е. функция Ферми – Дирака совпадает по форме с функцией Больцмана.
С помощью функции Ферми – Дирака можно ввести критерий вырождения полупроводника: если Fn(E, Т) << 1, то полупроводник не вырожден. Степень вырождения наступает при концентрации примеси N > 1018 см–3.
5.2. Концентрация носителей зарядов в полупроводнике
Функция Ферми – Дирака позволяет определить концентрацию подвижных носителей зарядов в полупроводнике при условии, что известна плотность квантовых уровней как в валентной, так и в зоне проводимости для дырок и электронов соответственно. Согласно квантовой теории, плотность квантовых уровней в зоне проводимости равна [9]
N(E) = (4p / h3)(2mn)3 / 2(Е – Е c)1 / 2 = Nc(E – Ec)1 / 2. (5.6)
Аналогично в валентной зоне
N(E) = (4p / h3)(2mp)3 / 2(Ev – E)1 / 2 = Nv(Ev – E)1 / 2, (5.7)

|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 10 11 12 |




