Основы стандартизации, сертификации и метрологии (стр. 8 )

Например: 1 пФ (пикофарада) = 10-12 Ф; наносекундный импульс - импульс, длительность которого 10-9 с; 1 мкВ (микровольт) =10-6 В и т. д.

Таблица 4

Приставки для образования кратных и дольных единиц

6. 4. Классификация измерений

В зависимости от способа получения числового значения измеряемой величины измерения подразделяются на прямые, косвенные, совокупные и совместные.

Прямое измерение - измерение, при котором искомое значение величины находят непосредственно из опытных данных в результате выполнения измерений.

При прямых измерениях числовое значение измеряемой величины отсчитывается непосредственно по показаниям измерительных приборов. Символически прямое измерение может быть выражено формулой

Y»X,

где Y - истинное значение измеряемой величины;

X - показание измерительного прибора.

К этому виду измерений относятся, например, измерения тока амперметром, напряжения источника - вольтметром и т. д.

Косвенное измерение - измерение, при котором искомое значение величины находят на основании известной зависимости между этой величиной и величинами, подвергаемыми прямым измерениям.

К этому виду измерений относится, например, косвенное измерение сопротивления резистора R путем прямых измерений напряжения и тока, связанных с искомой величиной сопротивления зависимостью

где R - сопротивление, Ом;

u - напряжение, В;

I - ток, А.

Измерение мощности постоянного тока амперметром и вольтметром с использованием зависимости, связывающей мощность постоянного тока с током и напряжением, а также нахождение плотности тела по его массе и геометрическим размерам следует отнести к косвенным измерениям.

Совокупными измерениями называются производимые одновременно измерения нескольких одноименных величин, при которых искомые значения величин находят решением системы уравнений, составленных из результатов прямых измерений различных сочетаний этих величин.

Пример совокупного измерения: измерение сопротивлений резисторов, соединенных треугольником, путем измерений сопротивлений между различными вершинами треугольника; по результатам трех измерений определяют сопротивления резисторов.

При совместных измерениях производятся одновременные измерения двух или нескольких неодноименных величин для нахождения зависимости между ними. Результат измерения получают путем решения системы уравнений.

По характеру точности различаются равноточные измерения и неравноточные измерения.

Равноточные измерения - ряд измерений какой-либо величины, выполненных одинаковыми по точности средствами измерений и в одних и тех же условиях c одинаковой тщательностью.

Неравноточные измерения - ряд измерений какой-либо величины, выполненных различающимися точности средствами измерений и (или) в разных условиях.

По количеству измерительной информации различают однократные измерения и многократные измерения.

Однократное измерение - измерение, выполненное один раз, причем число измерений равняется числу измеряемых величин. Недостатком этих измерений является возможность грубой ошибки – промаха. Для предотвращения этого рекомендуется проводить не менее 2-3-х измерений и за результат измерения принимать их среднее значение.

Многократное измерение - измерение одного и того же размера физической величины, результат которого получен из нескольких следующих друг за другом измерений, т. е. состоящее из ряда однократных измерений, при этом число измерений превышает число измеряемых величин в m/n раз, где m – число измеряемых величин, n - число измерений каждой величины. Обычно n³3. Многократные измерения проводят с целью уменьшения влияния случайных составляющих погрешностей измерений.

По характеру изменения получаемой информации в процессе измерений измерения разделяются на статические измерения и динамические измерения.

Статическое измерение - измерение физической величины, принимаемой в соответствии с конкретной измерительной задачей за неизменную на протяжении времени измерения. Они проводятся при практическом постоянстве измеряемой величины.

Пример. Средство измерений работает в статическом режиме. Выходной сигнал средства измерений, например отклонение указателя, остается неизменным в течение времени использования выходного сигнала, следовательно, измерение - статическое.

К статическим измерениям можно отнести измерения размеров детали, измерения напряжения и сопротивления резистора постоянного тока. Пределы допускаемых отклонений не существенны по отношению к номинальному значению измеряемой величины.

Динамическое измерение - измерение изменяющейся по размеру физической величины, для получения результата измерения которой необходимо учитывать это изменение. К этим измерениям можно отнести измерение переменного тока, измерение параметров периодических и апериодических сигналов. Результат измерения в этом случае представляется изменяющейся во времени величиной и представляется совокупностью ее значений с указанием моментов времени, которым соответствуют эти значения.

По метрологическому назначению используемых средств измерений измерения подразделяются на технические и метрологические.

Технические измерения - измерения с помощью рабочих средств измерений.

Метрологические измерения - измерения при помощи эталонов и образцовых средств измерений с целью воспроизведения единиц физических величин для передачи их размера рабочим средствам измерений.

По отношению к основным единицам измерения делятся на абсолютные измерения и относительные измерения.

Абсолютное измерение - измерение, основанное на прямых измерениях одной или нескольких основных величин и (или) использовании значений физических констант. Абсолютное измерение рассматривается как измерение величины в ее единицах.

Относительное измерение - измерение отношения величины к одноименной величине, играющей роль единицы, или изменения величины по отношению к одноименной величине, принимаемой за исходную.

Пример. Измеритель скорости у сверхзвукового самолета, показывающий отношение скорости самолета к скорости звука, или указатель расхода бензина в автомобилях проводят относительные измерения указанных величин.

6.5. Методы измерений

Взаимодействие СИ с объектом основано на физических явлениях, совокупность которых составляет принцип измерений, а совокупность приемов использования принципов и СИ называется методом измерений. Числовое значение измеряемой величины получается путем ее сравнения с известной величиной, воспроизводимой определенным видом СИ - мерой. В зависимости от способа применения меры известной величины выделяют метод непосредственной оценки и метод сравнения с мерой. Основными наиболее общими методами измерений являются метод непосредственной оценки и методы сравнения с мерой: нулевой метод, дифференциальный метод, метод замещения и метод совпадений.

При измерениях методом непосредственной оценки значение измеряемой величины определяют непосредственно по отсчетному устройству измерительного прибора прямого преобразования, шкала которого заранее была проградуирована с помощью многозначной меры, воспроизводящей известные значения измеряемой величины.

В приборах прямого преобразования в процессе измерения оператором производится сравнение положения указателя отсчетного устройства и шкалы, по которой производится отсчет. Измерение силы тока с помощью амперметра - пример измерения по методу непосредственной оценки.

В основе применения данного метода лежит использование того или иного физического явления, на котором основан принцип действия измерительного прибора. Так, например, измерение постоянного тока методом непосредственной оценки может быть выполнено на основе использования механического взаимодействия магнитного поля и измеряемого тока. Аналогичным образом определение напряженности поля производится на основе использования явления электромагнитной индукции путем оценки величины э. д.с., индуцированной в антенне измеряемым полем, и т. д.

Отличительной чертой методов сравнения является непосредственное участие в процессе измерения меры известной величины, однородной с измеряемой. Сравнение может быть непосредственным или опосредствованным через другие величины, однозначно связанные с первыми. Группа методов сравнения с мерой включает в себя следующие методы: нулевой, дифференциальный, замещения и совпадения.

При нулевом методе измерения разность измеряемой величины и известной величины или разность эффектов, производимых измеряемой и известной величинами, сводится в процессе измерения к нулю, что фиксируется высокочувствительным прибором - нуль-индикатором. При высокой точности мер, вопроизводящих известную величину, и высокой чувствительности нуль-индикатора может быть достигнута высокая точность измерений. При измерении нулевым методом измеряемая величина уравновешивается известной величиной, воспроизводимой мерой так, что в результате они не оказывают воздействия на индикаторное устройство, указатель которого дает нулевое показание. Типичными примерами нулевого метода являются измерения сопротивления, индуктивности и емкости мостовыми схемами или тока и напряжения компенсационными устройствами.

Дифференциальный метод измерения состоит в том, что измеряемая величина сравнивается с известной величиной, воспроизводимой мерой, и полученная разность отсчитывается измерительным прибором. Таким образом, в отличие от нулевого метода в этом случае измеряемая величина уравновешивается не полностью. При дифференциальном методе разность измеряемой величины и величины известной, воспроизводимой мерой, измеряется с помощью измерительного прибора. Неизвестная величина определяется по известной величине и измеренной разности. Дифференциальный метод также может обеспечить высокую точность измерения, если известная величина воспроизводится с высокой точностью и разность между ней и неизвестной величиной мала.

Метод замещения состоит в том, что измеряемая величина заменяется известной величиной, воспроизводимой мерой, значение которой подбирается таким образом, чтобы показание индикаторного прибора в измерительной схеме осталось неизменным. Метод замещения применяется при прецизионных измерениях сопротивления, индуктивности и емкости, при измерении напряженности поля и в ряде других случаев.

Метод совпадений - метод сравнения с мерой, в котором разность между измеряемой величиной и величиной, воспроизводимой мерой, измеряют, используя совпадение отметок шкал или периодических сигналов.

6.6. Виды средств измерений

По техническому назначению все средства измерений (СИ) подразделяют на меры, измерительные преобразователи, измерительные приборы, измерительные системы и измерительные установки.

Мера - средство измерений, предназначенное для воспроизведения и (или) хранения физической величины одного или нескольких заданных размеров, значения которых выражены в установленных единицах и известны с необходимой точностью. Мерами являются, например, гири, линейки с делениями, измерительная колба, генератор стан­дартных сигналов и др. Меры подразделяются на однозначные, многозначные, наборы мер, магазины мер. Однозначная мера - это мера, воспроизводящая физическую величину одного размера, например, гиря 1 кг, конденсатор постоянной емкости. Многозначная мера - это мера, воспроизводящая физическую величину разных размеров, например, конденсатор переменной емкости. Набор мер – это комплект мер разного размера одной и той же физической величины (например, набор гирь), необходимый для применения на практике как в отдельности, так и в различных сочетаниях. Если наборы мер объе­динены в одно конструктивное целое с приспособлением для соеди­нения их в различных комбинациях, то в этих случаях говорят о магазинах мер (например, магазины сопротивлений).

Измерительный преобразователь - средство измерений, служащие для пре­образования измеряемой величины в другую однородную или неоднородную величину с целью представления измеряемой величины в форме, удобной для передачи, дальнейшего преобразования, обработки и хранения (например, в памяти ЭВМ), но не поддающейся непосредственному восприятию наблюдателем. Измерительные преобразователи не имеют устройств отображения измерительной информации, они или входят в состав измерительных приборов (установок), или применяются совместно с ними (например, делители напряжения, усилители, чувствительные элементы измерительных приборов, датчики).

Измерительные приборы - средства измерений, предназначенные для выработки сигнала измерительной информации в форме, доступной для непосредственного восприятия наблюдателем, например, в виде цифрового отсчета на отсчетном устройстве. В отличие от мер измерительные при­боры не воспроизводят измеряемой величины. Она подводит­ся к ним извне. В состав измерительного прибора входят уз­лы и детали, служащие для восприятия и преобразования воздействующего на прибор сигнала от объекта измерения. К измерительным приборам относятся разного рода вольтмет­ры, амперметры, частотомеры и пр.

Измерительная система – совокупность объединенных измерительных, вычислительных и других технических средств, размещенных в разных точках контролируемого пространства, для получения измерительной информации, ее преобразования, обработки с целью представления потребителю в требуемом виде либо для автоматического контроля, диагностирования, идентификации.

Свойства СИ оцениваются характеристиками, среди которых выделяют комплекс метрологических характеристик, т. е. характеристик, которые необходимы при оценке точности результатов измерений.

Метрологическая характеристика СИ – характеристика одного из свойств измерений, влияющая на результат измерений и на его погрешность. Важным отличительным признаком СИ является наличие у них нормированных метрологических характеристик, благодаря чему при надлежащем применении СИ может быть оценена точность получаемых результатов измерений.

Нормируемые метрологические характеристики СИ - совокупность метрологических характеристик для данного типа СИ, устанавливаемая нормативно-техническими документами.

Обобщенной метрологической характеристикой СИ является класс точности, определяемый пределами допускаемых погрешностей и другими свойствами СИ, влияющими на точность результатов измерений. Реально в эксплуатации находится огромное количество самых разнообразных средств измерений, имеющих отличительные признаки по своим свойствам, по конструкции исполнения, по условиям применения и т. д. Соответственно и контроль качества проведения измерений, особенно контроль качества каждого единичного измерения, представляется чрезвычайно сложным. Для решения этой задачи, т. е. для обеспечения необходимого качества проведения измерений, необходимо обеспечить единообразие средств измерений.

6.7. Классификация средств измерений

Для удобства установления единых требований к средствам измерений их классифицируют по весьма разнообразным признакам.

Принцип действия. Физическую величину можно измерить при помощи средств измерений, отличающихся друг от друга принципом действия. Различия этих принципов свя­заны с использованием разных физических явлений. В зави­симости от принципа действия данного устройства точность его может быть неодинакова.

Способ образования показаний. По способу образования показаний измерительные приборы можно разделить на показывающие (в том числе и цифровые) и самопишущие.

Способ получения числового значения измеряемой величины. Здесь можно выделить две группы: приборы непосредственной оценки и приборы сравнения. В свою очередь измерительные приборы непосредственной оценки можно разделить на приборы, показывающие значения измеряемой величины, существующей в данный момент времени, и интегрирую­щие. Приборы сравнения (компарирующие приборы) предназначены для сравнения мер между собой и измеряемой величины с мерами.

Точность средств измерения определяется уровнем основных и дополнительных погрешностей. С целью упорядочения (стандартизации по точности) каждый вид средств измерения делится на классы точности. Например, электроизмерительные приборы имеют следующие классы точности: 0,1; 0,2; 0,5; 1,0; 1,5; 2,5; 4,0.

Условия применения. К этому признаку относятся температура, влажность, атмосферное давление, рабочее напряжение сети, диапазон частот и т. д. Условия применения средств измерений задаются указа­нием значений величин внешних факторов, влияющих на работу данного средства. Для каждого средства измерения определяют обычно четыре области условий применения.

Нормальные условия - самые удобные для измерения.

Рабочие условия - при которых средство является пригодным для измерений.

Предельные условия - при которых средство не обязательно пригодно к измерению, но их кратковременное действие не выводит его из строя.

Условия хранения - условия, которые обеспечивают сохранность средства измерения в течение длительного времени. Независимо от рабочих условий они должны быть всегда более жесткими, чем предельные.

Степень защищенности от влияния внешних магнитных и электрических полей. Для электроизмерительных приборов введены, например, две категории защищенности: I (более защищенные) и II (ГОСТ 1845—59).

Прочность и устойчивость против механических воздействий и перегрузок. По степени защиты от внешних воздействий различают средства измерений обыкновенные, пылезащищенные, брызгозащищенные, водозащищенные, герметические, газозащищенные, взрывоопасные.

Стабильность показаний средств измерений - это свойство сохранять неизменными погрешности длительное время. Причиной изменения показания измерительных приборов могут, кроме внешних воздействий, являться внутренние, структурные изменения материалов, из которых изготовлены основные детали средства измерений, по истечении более или менее длительного времени. Поэтому при нормировании требований по стабильности показаний необходимо учитывать конструкционные особенности, вызывающие со временем износ определенных деталей.

Чувствительность. Под чувствительностью измерительного устройства понимают его способность реагировать на изменение измеряемой величины. Эта характеристика является наряду с точностью одной из важнейших для измерительных приборов.

Пределы и диапазоны измерения. Важные характеристики любого средства измерения, определяющие пригодность его для тех целей, для которых он предназначен.

Классификация измерительных средств по признакам для различных средств неодинакова. Так, к одним видам средств измерений применимы только некоторые из перечисленных выше признаков. Наибольшее число признаков охватывает классификация электроизмерительных приборов.

6.8. Результат измерения и виды погрешностей

Результат измерения практически всегда отличается от истинного значения физической величины - значения, которое выражает размер величины абсолютно точно. Истинное значение физической величины определить невозможно. Это связано с несовершенством наших органов чувств или соответствующих технических средств и всегда сопряжено с погрешностями, искажающими представление о действительном (истинном) значении измеряемой величины. В зависимости от степени совершенства знаний, средств измерений, условий, в которых проводится измерение, получают различную степень приближения результата измерения к истинному значению измеряемой величины.

Результат измерения есть значение физической величины, полученное путём её измерения.

Погрешность измерения - отклонение результата измерения от истинного значения измеряемой величины.

Истинное значение физической величины – это значение физической величины, которое идеальным образом характеризовало бы в качественном и количественном отношении соответствующую физическую величину. Если обозначить Х - измеренное значение, а Y - истинное значение измеряемой величины, то погрешность измерения будет D = Х – Y. Истинное значение физической величины неизвестно и применяется только в теоретических исследованиях, на практике же применяется действительное значение величины, которое определяется экспериментально при условии, что результат измерения наиболее приближен к истинному значению величины.

Действительное значение физической величины - значение физической величины, полученное экспериментальным путем и настолько близкое к истинному значению, что в поставленной измерительной задаче может быть использовано вместо него. Источниками погрешностей являются недостатки измерительных приборов, несовершенство органов чувств наблюдателя, непостоянство условий наблюдения и др. Для того, чтобы результаты измерений, полученные в разных условиях, разными специалистами, на различных средствах измерений были бы сравнимы, необходимо обеспечить единство измерений. Работы по обеспечение единства измерений и единообразия средств измерений являются основной задачей метрологии.

Часто применяют понятие «точность измерения», имея в виду качество измерения, отражающее близость результата измерения к истинному значению измеряемой величины. Высокая точность измерения соответствует малым значениям погрешностей измерений.

По форме представления погрешности разделяются на абсолютные, относительные и приведенные.

Абсолютная погрешность измерения равна разности между измеренным и истинным значением измеряемой величины:

D = Х – У, (2)

где У - истинное значение измеряемой величины;

Х - измеренное значение;

D - абсолютная погрешность измерения

В случае использования при измерении меры, абсолютная погрешность определяется как разность между номинальным значением меры и истинным (действительным) значением измеряемой величины.

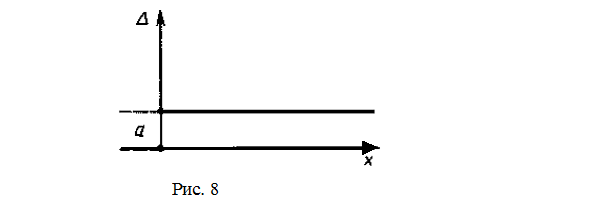
В случае использования при измерении измерительного прибора, абсолютная погрешность определяется как разность между показанием прибора и истинным (действительным) значением измеряемой величины. Показание прибора – значение измеряемой величины, определяемое по отсчетному устройству. Так, например, если показание вольтметра равно 127 В, а истинное значение напряжение, за которое принимаем показание образцового прибора, равно 125 В, то абсолютная погрешность вольтметра составит D=2 В. Абсолютная погрешность выражается в единицах измеряемой величины. Уравнение (2) характеризует как величину абсолютной погрешности, так и ее знак, т. е., если Х>У, абсолютная погрешность берется со знаком плюс, а если У>Х – со знаком минус. Абсолютная погрешность может быть выражена одним числом, в виде одночленной формулы D=±а, где а – числовое значение измеряемой величины, не зависящее от Х, либо двучленной формулой D=±(a+bX), где Х – измеряемая величина; a и b – постоянные величины; D – абсолютная погрешность измеряемой величины. Коэффициент a определяет составляющую погрешности остающуюся постоянной во всем диапазоне измерений. Эта составляющая называется аддитивной погрешностью. График аддитивной погрешности приведен на рис. 8.

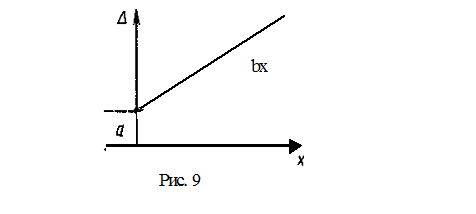
Составляющая погрешности, линейно зависящая от значения измеряемой величины, называется мультипликативной погрешностью и определяется коэффициентом b. График аддитивной погрешности приведен на рис. 9.

Величина абсолютной погрешности не характеризует еще точности измерения. Для суждения о точности измерения нужно сопоставить абсолютную погрешность с истинным значением измеряемой величины.

Отношение абсолютной погрешности измерения к истинному значению измеряемой величины называется относительной погрешностью измерения. Относительная погрешность может быть одночленной формулой

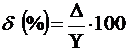(3)

или двучленной формулой

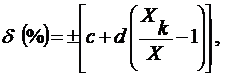(4)

где δ – предел допускаемой относительной погрешности в процентах от значения измеряемой величины;

Хк - конечное значение диапазона измерений;

с и d – положительные числа.

Коэффициент с численно равен относительной погрешности на верхнем пределе измерения, d - численно равен погрешности на верхнем пределе измерения, выраженной в процентах от верхнего предела.

В реальной практике вместо истинного значения используют максимально приближенное к нему действительное значение измеряемой величины Хд. Допускается вместо Хд в данной формуле использовать показания измерительного прибора Х.

Для предыдущего числового примера относительная погрешность измерения напряжения

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8 9 10