–394,4 0 –50,8 –228,4
значения ![]() всех участников реакции известны и приведены под уравнением (в кДж/моль).
всех участников реакции известны и приведены под уравнением (в кДж/моль).
Тогда для реакции
![]() = –50,8 – 2·228,4 + 394,4 = –113,2 кДж/моль.
= –50,8 – 2·228,4 + 394,4 = –113,2 кДж/моль.
Отсюда легко рассчитать константу равновесия при 298 К:
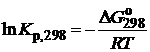
и, следовательно, значение константы равновесия при температуре процесса.
Определение констант равновесия сложных реакций осуществляют комбинированием простых реакций. При этом важно выделить и учесть каждую из составляющих простых реакций. Комбинирование необходимо проводить таким образом, чтобы через константы, известные и приводимые в таблицах, можно было выразить константы более сложных реакций или получить по известным константам неизвестные.
Так, для последовательных превращений
1) А + B ![]() R
R
 2) R
2) R ![]() S + Z
S + Z
A + B ![]() S + Z
S + Z
константа равновесия суммарной реакции равна произведению констант равновесия составляющих ее простых реакций:
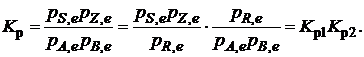
Соответственно, суммарное изменение энергии Гиббса равно сумме ее изменений для отдельных реакций:
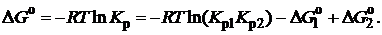
Определение состава реакционной смеси при химическом равновесии. Рассмотрим связь константы равновесия Kр и равновесной степени превращения хa,е для газовой реакции А ![]() 2R.
2R.
После установления равновесия на 1 моль введенного вещества реакционная смесь будет содержать (1 – хa,е) моль реагента А и 2хa,е моль продукта R. Всего в равновесном состоянии будет находиться
1 – хa,е + 2хa,е = = 1 + хa,е моль. Если общее давление системы в момент равновесия равно р, можем записать равновесные парциальные давления компонентов согласно выражению (2.8):
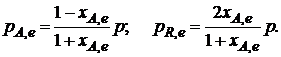
Тогда связь между константой равновесия и равновесной степенью превращения выразится уравнением
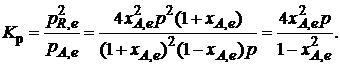
Получили простое уравнение, из которого видно также влияние давления: при постоянной температуре снижение общего давления ведет к увеличению хa,е. Перегруппировав это выражение, получаем
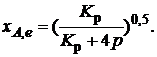 (2.10)
(2.10)
Расчетная формула (2.10) позволяет найти значения хa,е для разных давлений при постоянной температуре и, следовательно, рассчитать равновесный состав смеси. На рис. 2.1 приведена зависимость равновесной степени превращения реагента хa,е при протекании реакции А ![]() 2R от относительного давления
2R от относительного давления ![]() = р/р0, где р0 – стандартное давление, равное 0,098 МПа.
= р/р0, где р0 – стандартное давление, равное 0,098 МПа.
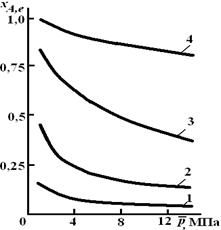
Рис. 2.1. Зависимость равновесной степени превращения
обратимой реакции А 2R от давления для разных значений
константы равновесия Кр: 1 – 0,1; 2 – 1,0; 3 – 10,0; 4 – 100,0
Пример 2.1. Рассмотрим расчет равновесия по известным значениям Kр для реакции окисления диоксида серы:
SO2 + 0,5О2 + zN2 ![]() SO3 + zN2,
SO3 + zN2,
a b n
где а, b, n – количество (моль) компонентов исходной смеси SO2, O2, N2, (а + b + n) = 1.
Количество каждого компонента (моль) при достижении равновесной степени превращения хA,е составит
SO2 O2 N2 SO3
а – ахA,е b – 0,5ахA,е n ахA,е
Общее число молей равновесной смеси
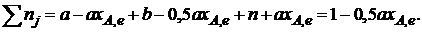
Обозначив общее давление через р, выразим равновесные давления компонентов:
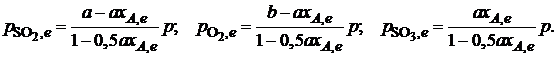
Тогда
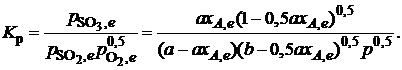
Отсюда
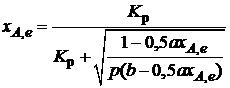 . (2.11)
. (2.11)
Найдем состав равновесной смеси, если в исходной смеси содержится 7 % SO2, 11 % О2, 82 % N2.
При T = 650 К константа равновесия Кр = 629. Подставляя исходные данные в уравнение (2.11), получим
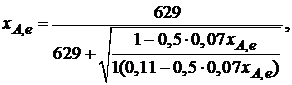
откуда находим хA,е = 0,994 и, следовательно, в равновесной смеси содержится (моль): SO3 – 0,069, SO2 – 0,001, О2 – 0,076, N2 – 0,82.
В приведенном примере рассмотрена реакция, протекающая с уменьшением числа молей (∆n < 0). Полученная расчетная формула (2.11) наглядно иллюстрирует зависимость равновесной степени превращения от давления в системе – повышение общего давления ведет за собой увеличение хA,е.
Вопросы и упражнения
для повторения и самостоятельной работы
1. Сформулируйте основной круг задач, решаемых в химической технологии при выборе технологического режима на основании законов химической термодинамики.
2. Как определить направленность химической реакции? Как, сравнивая значения энергии Гиббса ∆G для различных реакций, определить, какая из них является спонтанной (самопроизвольной)?
3. Сформулируйте основные условия устойчивого равновесия.
4. Что характеризует химическое равновесие?
5. Вычислите величины Кc, KN, Кn для равновесной реакции
С6Н5 – С2Н5 ![]() С6Н5 – СН = СН2 + Н2,
С6Н5 – СН = СН2 + Н2,
если при температуре 580 °С найдена Kр = 0,20, общее давление р = 0,005 МПа.
6. Сформулируйте принцип Ле Шателье. Как он помогает предсказать влияние изменения температуры и давления на состояние равновесия химической реакции?
7. Используя принцип Ле Шателье, проанализируйте для приведенных реакций все возможные способы смещения равновесия вправо:
N2 + 3H2 ![]() 2NH3 ∆H < 0;
2NH3 ∆H < 0;
CH4 + H2O ![]() CO + 3H2 ∆H > 0;
CO + 3H2 ∆H > 0;
СО + Н2О ![]() СО + Н2 ∆H < 0;
СО + Н2 ∆H < 0;
2С2Н5ОН ![]() С4Н6 + 2Н2О + Н2 ∆Н > 0.
С4Н6 + 2Н2О + Н2 ∆Н > 0.
8. Выведите уравнение для расчета равновесной степени превращения реагента А по известной величине Кc (для реакции 2А ![]() R).
R).
9. Выведите уравнение для расчета равновесной степени превращения реагента А по известным значениям Кр и давления р в системе для реакции А + В ![]() R.
R.
10. Выведите уравнение для расчета равновесного состава участников реакции синтеза аммиака по известным значениям Kp, и давления p в системе.
11. Рассчитайте константу равновесия для реакции СО2 + С![]() 2СО, если известно, что для СО2
2СО, если известно, что для СО2 ![]() = –394572 и для СО
= –394572 и для СО ![]() = –137334 Дж/моль.
= –137334 Дж/моль.
12. Найдите константу равновесия при температурах 500 и 2000 К для реакции Н2О + СО ![]() Н2 + СО2, если
Н2 + СО2, если 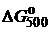 = 20,2 кДж/моль и
= 20,2 кДж/моль и ![]() = 25,3 кДж/моль.
= 25,3 кДж/моль.
13. Почему можно исключить из выражения для константы равновесия концентрации компонентов, являющихся чистыми твердыми веществами или жидкостями?
Глава 3
ИСПОЛЬЗОВАНИЕ ЗАКОНОВ ХИМИЧЕСКОЙ
КИНЕТИКИ ПРИ ВЫБОРЕ ТЕХНОЛОГИЧЕСКОГО
РЕЖИМА И МОДЕЛИРОВАНИИ
ХИМИЧЕСКИХ ПРОЦЕССОВ
Химическая термодинамика позволяет решать вопрос о направлении протекания химических реакций и оценить предельно достижимые (равновесные) состояния реакционной системы. Однако она не может ответить на вопросы, имеющие чрезвычайно важное практическое значение в химической технологии: как быстро произойдет химическое превращение, за какой промежуток времени будет получено то или иное количество продукта реакции.
Решающее значение при выборе условий проведения химико-технологических процессов имеют вопросы скорости химических превращений, изучаемые химической кинетикой.
Для химической технологии важен конечный результат кинетических исследований – конкретный вид уравнения, позволяющего рассчитывать скорость химической реакции при различных условиях ее проведения. Кинетические уравнения, содержащие необходимую информацию об основных закономерностях химических превращений, являются первоосновой математической модели химического реактора. Без знания кинетических закономерностей невозможно правильно выбрать тип реактора и рассчитать его конструктивные размеры.
Вопросы изучения кинетики химических реакций, определения кинетических параметров подробно рассматриваются в руководствах по физической химии и химической кинетике. Здесь основное внимание будет обращено на практические приложения результатов кинетических исследований.
§ 3.1. Скорость гомогенных химических реакций
Скорость химической реакции wrJ принято выражать количеством (моль) nJ одного из реагентов или продуктов, прореагировавшим (или образовавшимся) в единицу времени τ в единице реакционного пространства.
Для гомогенной химической реакции
![]() (3.1)
(3.1)
где V – реакционный объем.
Скорость химической реакции может быть измерена по любому компоненту, участвующему в реакции. Она всегда положительна, поэтому знак перед производной dnJ /dτ должен определяться тем, является ли вещество J исходным реагентом (тогда dnJ/dτ отрицательна) или продуктом (тогда dnJ/dτ положительна). Иногда нельзя определенно сказать, является ли вещество J реагентом или продуктом. Например, при протекании последовательных реакций
A ![]() R,
R,
R ![]() S
S
вещество R является продуктом по отношению к первой стадии и реагентом по отношению ко второй. В этом случае необходимо, чтобы знак перед производной находился в определенном соответствии со знаками в кинетическом уравнении (см. § 3.2).
В том случае, если реакция протекает при постоянном объеме, скорость определяют как изменение молярной концентрации с в единицу времени:
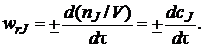 (3.2)
(3.2)
Если химическая реакция описывается стехиометрическим уравнением
аА + bB + сС +… ![]() rR + sS + qQ...,
rR + sS + qQ...,
то изменения количеств реагентов и продуктов ![]() , в результате ее протекания связаны между собой соотношениями (1.3). Скорости реакции, определенные по изменению количества различных реагентов в соответствии с уравнениями (3.1) или (3.2), количественно различаются между собой, если не равны стехиометрические коэффициенты у этих реагентов.
, в результате ее протекания связаны между собой соотношениями (1.3). Скорости реакции, определенные по изменению количества различных реагентов в соответствии с уравнениями (3.1) или (3.2), количественно различаются между собой, если не равны стехиометрические коэффициенты у этих реагентов.
В то же время из уравнений (3.1) и (1.3) следует, что для скоростей реакции, рассчитанных по изменению количества разных реагентов или продуктов, будет выполняться условие
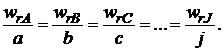
Такая ситуация создает некоторые неудобства в количественном определении скорости реакции, так как измеренная по изменению количеств различных реагентов скорость одной и той же реакции будет выражаться различными числовыми значениями. Для устранения этого неудобства далее будем определять скорость реакции по уравнению
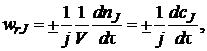 (3.3)
(3.3)
где j – стехиометрический коэффициент у компонента J, по которому рассчитывают скорость реакции.
Тогда скорость «приводится к общему знаменателю» и независимо от того, по изменению количества какого конкретного реагента или продукта она определялась, численно будет одинакова, т. е.
![]()
Экспериментально скорость химической реакции определяют, изучая изменение во времени количества (или концентрации) некоторого реагента или продукта.
Численно скорость реакции выражают в единицах концентрации, отнесенных к единице времени, например: кмоль·м–3·ч–1; моль·л–1·с–1 и т. д.
§ 3.2. Зависимость скорости химических реакций
от концентрации реагентов. Кинетические уравнения
Скорость химического превращения зависит от большого числа переменных. Результаты экспериментальных исследований различных реакций показали, что на скорость влияют не только факторы, определяющие состояние химического равновесия (температура, давление, состав реакционной системы), но и иные причины, такие, как наличие или отсутствие посторонних веществ, не претерпевающих изменений в результате реакции, условия физической транспортировки реагентов к реакционным центрам и др.
Факторы, оказывающие влияние на скорость химического превращения, обычно подразделяют на две группы:
– чисто кинетические (микрокинетические), определяющие скорость взаимодействия на молекулярном уровне;
– макрокинетические, определяющие влияние на скорость реакции условий транспорта реагентов к зоне реакции, наличия или отсутствия перемешивания, геометрических размеров реактора.
Рассмотрим сначала влияние микрокинетических факторов на скорость химических реакций.
Законы химической кинетики основаны на двух простых принципах (постулатах), впервые установленных при изучении реакций в растворах:
скорость химической реакции пропорциональна концентрациям реагентов;
суммарная скорость нескольких последовательных превращений, широко различающихся по скорости, определяется скоростью наиболее медленной стадии.
Функциональная зависимость скорости химической реакции от концентраций компонентов реакционной смеси
wr = wr (cA, сВ, ..., сJ)
называется кинетическим уравнением реакции.
В химической кинетике принято делить химические реакции на элементарные и неэлементарные (сложные).
Элементарными (одностадийными) называются реакции, осуществление которых связано с преодолением одного энергетического барьера при переходе из одного состояния реакционной системы в другое. Механизм такой реакции соответствует ее стехиометрическому уравнению.
Кинетическое уравнение необратимой элементарной реакции
аА + bB ![]() rR + sS (I)
rR + sS (I)
в соответствии с первым постулатом, основанном на законе действующих масс, имеет вид
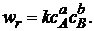 (3.4)
(3.4)
Коэффициент пропорциональности k, входящий в кинетическое уравнение (3.4), называют константой скорости химической реакции. Целочисленные показатели степени а и b у концентраций реагентов А и В в кинетическом уравнении (3.4) для элементарной реакции называются порядками реакции по реагентам соответственно А и В. Их сумма а + b = n называется общим порядком реакции. Для элементарных реакций частные порядки (порядки реакций по отдельным реагентам) равны соответствующим стехиометрическим коэффициентам в уравнении реакции.
Наряду с понятием «порядок реакции» в химической кинетике используют понятие «молекулярность реакции». Молекулярность реакции равняется минимальному числу молекул, одновременно принимающих участие в одном элементарном акте реакции.
Для элементарных реакций порядок равен молекулярности и может иметь значения 1, 2, 3. Порядок (или молекулярность) элементарных реакций не превышает значения 3, так как вероятность одновременного столкновения более чем трех молекул чрезвычайно низка.
Однако большинство химических реакций не являются элементарными: они протекают через ряд промежуточных стадий. Стехиометрическое уравнение неэлементарной (сложной) реакции отражает лишь начальное и конечное состояния данной реакционной системы и не описывает механизм реакции.
Сложную реакцию иногда удобно рассматривать как формально простую, т. е. считать, что она протекает в одну, а не в несколько стадий. Так можно поступить, если в условиях рассматриваемой задачи промежуточные продукты не обнаруживаются.
Для формально простой реакции
аА + bВ + dD ![]() rR + sS + qQ
rR + sS + qQ
кинетическое уравнение по аналогии с простой (элементарной) реакцией можно записать в следующем виде:
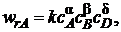
где частные порядки реакции α, β и δ находят экспериментально. В общем случае α ≠ a, β ≠ b, δ ≠ d, т. е. молекулярность и порядок реакции не совпадают. Полный порядок реакции п = α + β + δ и частные порядки в таком уравнении могут быть целочисленными, но могут быть и дробными, так как закон действующих масс, предполагающий целочисленные показатели степеней у концентраций в кинетическом уравнении, строго применим только к элементарным реакциям.
Наряду с неэлементарными реакциями, которые можно рассматривать как формально простые, существует много сложных реакций, которые явно распадаются на стадии (продукты различных стадий образуются в значительных количествах).
Простейшими типами сложных реакций являются параллельные и последовательные реакции.
В параллельных реакциях взаимодействие одних и тех же реагентов может протекать по различным реакционным путям с образованием различных продуктов. В качестве примера можно указать на параллельные реакции окисления аммиака, продуктами которых могут быть или оксид азота NО, или оксид диазота N2О, или азот N2.
В последовательных реакциях продукт первой реакции является исходным реагентом для второй. Реакция может состоять как из двух, так и из большего числа стадий, следующих друг за другом. Примером таких реакций могут служить реакции расщепления углеводородов с длинной углеродной цепочкой на все более мелкие молекулы.
В случае если известен механизм сложной реакции (элементарные стадии, через которые она протекает), скорость реакции по одному из веществ – ее участников – равна алгебраической сумме скоростей тех элементарных стадий, в которых это вещество принимает участие.
При определении знаков у членов этой суммы удобно пользоваться формальным правилом: производной концентрации данного компонента по времени dcJ /dτ приписывают знак минус независимо от того, является ли компонент J исходным реагентом или продуктом реакции; скорости элементарных стадий, в которых компонент J расходуется (является реагентом), записывают в общей сумме со знаком плюс, скорости стадий, в которых компонент J образуется (является продуктом), – со знаком минус.
Пример 3.1. Составим кинетическое уравнение по веществам R и А – участникам сложной реакции:
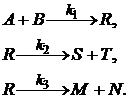
Эта реакция состоит из трех стадий. Вторая и третья стадии являются последовательными по отношению к первой и параллельны по отношению друг к другу. Скорость по компоненту R, участвующему во всех трех реакциях,
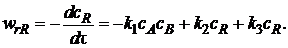
Скорость по исходному реагенту А, участвующему лишь в первой элементарной стадии,
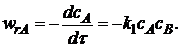
Пример 3.2. Обратимую реакцию
А+ В ![]() R+ S
R+ S
с точки зрения химической кинетики можно рассматривать как сложную, состоящую из двух стадий:
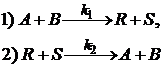

|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |



