ГЛАВА 6

ОПТИКА

28. ГЕОМЕТРИЧЕСКАЯ ОПТИКА

Основные формулы

• Фокусное расстояние сферического зеркала

f=R/2,

где R — радиус кривизны зеркала.

Оптическая сила сферического зеркала

Ф=1/f. Формула сферического зеркала

,

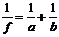где а и b — расстояния от полюса зеркала соответственно до пред­мета и изображения.

Если изображение предмета мнимое, то величина b берется со знаком минус.

Если фокус сферического зеркала мнимый (зеркало выпуклое), то величина f берется со знаком минус.

• Закон преломления света

,

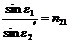где ε1 — угол падения; ε2’ — угол преломления; n21=n2/n1 — отно­сительный показатель преломления второй среды относительно пер­вой; n1 и n2 — абсолютные показатели преломления соответственно первой и второй сред.

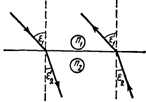
Нижние индексы в обозначениях уг­лов указывают, в какой среде (первой или второй) идет луч. Если луч перехо­дит из второй среды в первую, падая на поверхность раздела под углом ε2=ε2’, то по принципу обратимости све­товых лучей угол преломления ε1’ будет равен углу ε1 (рис. 28.1).

• Предельный угол полного отражения при переходе света из среды более оптически плотной в среду менее оптически плотную

εпр= arcsin(n2/n1) (n2<n1)

• Оптическая сила тонкой линзы

,

где f — фокусное расстояние линзы; nЛ — абсолютный показатель преломления вещества линзы; nср — абсолютный показатель пре­ломления окружающей среды (одинаковой с обеих сторон линзы).

В приведенной формуле радиусы выпуклых поверхностей (R1 и R2) берутся со знаком плюс, вогнутых — со знаком минус.

• Оптическая сила двух тонких сложенных вплотную линз

Ф=Ф1+Ф2.

• Формула тонкой линзы

,

где a — расстояние от оптического центра линзы до предмета; b —расстояние от оптического центра линзы до изображения.

Если фокус мнимый (линза рассеивающая), то величина f отри­цательна.

Если изображение мнимое, то величина b отрицательна.

• Угловое увеличение лупы

Г=D/f,

где D — расстояние наилучшего зрения (D=25 см).

• Угловое увеличение телескопа

Г = fоб/fок,

где fоб и fок — фокусные расстояния соответственно объектива и окуляра.

Расстояние от объектива до окуляра телескопа

L=fоб + fок

Эти формулы можно применять только в том случае, если в теле­скоп наблюдают весьма удаленные предметы.

• Угловое увеличение микроскопа

L=δD/(fоб/fок),

где δ — расстояние между задним фокусом объектива и передним фокусом окуляра.

Расстояние от объектива до окуляра микроскопа

L=fоб + δ + fок

Примеры решения задач

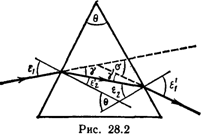
Пример 1. На стеклянную призму с преломляющим углом θ=50° падает под углом ε=30° луч света. Определить угол откло­нения σ луча призмой, если показатель преломления п стекла равен 1,56.

Решение. Данную задачу целесообразно решать не в общем виде, как принято, а пооперационно, производя все промежуточ­ные вычисления. В этом случае мы несколько проигрываем в точ­ности расчетов, но выигрываем в наглядности и простоте вычислений. Из рис. 28.2 видно, что угол отклонения

σ=γ+γ’, (1)

углы γ и γ’ просто выражаются через углы ε1,ε2’,ε1’,ε2, которые последовательно и будем вычислять:

1)  из закона преломления n=sin ε1/sin ε2’ имеем

°;

2)  из рис. 28.2, следует, что угол падения ε2 на вторую грань призмы равен

°.

Угол ε2 меньше предельного ε2пред=arcsin(1/n)= 39,9°, по­тому на второй грани луч преломится и выйдет из призмы;

3) так как sin ε2/sin ε1=l/n, то ε1’=arcsin(пsin ε2)=54,1°.

Теперь найдем углы γ и γ’:

γ= ε1— ε2’=11,3° и

γ’=ε1’—ε2=22,8°.

По формуле (1) находим σ=γ+γ’=34,1°.

Пример 2. Оптическая сис­тема представляет собой тон­кую плосковыпуклую стек­лянную линзу, выпуклая по­верхность которой посереб­рена. Определить главное фо­кусное расстояние f такой системы, если радиус кривиз­ны R сферической поверхно­сти линзы равен 60 см.

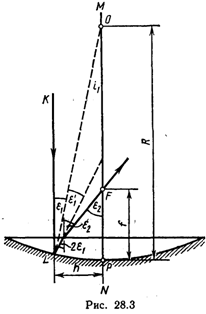
Решение. Пусть на линзу падает параксиальный луч KL, параллельный глав­ной оптической оси MN лин­зы (рис. 28.3). Так как луч KL перпендикулярен плоской поверхности линзы, то он проходит ее без преломления.

На сферическую посеребренную поверхность луч падает в точке L под углом ε1 и отражается от нее под углом ε1’=ε1. Отраженный луч падает на границу плоской поверхности линзы под углом 2ε1 и по выходе из линзы пересекает главную оптическую ось в точке F, образуя с осью угол ε2. Длина полученного при этом отрезка FP и равна искомому фокусному расстоянию рассматриваемой оптичес­кой системы.

Если учесть, что в силу параксиальности луча KL углы ε1 и ε2 малы, а их синусы и тангенсы практически равны самим углам, выраженным в радианах, то из рис. 28.3 следует

.

Входящее в формулу (1) отношение ε1/ε2 углов найдем, пользуясь законом преломления света, который в нашем случае записываете;

в виде 2ε1/ε2==l/n, откуда

ε1/ε2=l/(2n).

Подставив это отношение углов в формулу (1), найдем

f=R/(2n).

Такой же результат можно получить и из формальных соображений. Так как луч K.L последовательно проходит линзу, отражается от вогнутого зеркала и еще раз проходит линзу, то данную оптическую систему можно рассматривать как центрированную сис­тему, состоящую из сложенных вплотную двух плосковыпуклых линз и сферического зеркала. Фокусное расстояние оптической системы может быть найдено по формуле

f=1/Ф,

где Ф — оптическая сила системы.

Как известно, оптическая сила системы равна алгебраической сумме оптических сил отдельных компонентов системы. В нашем слу­чае

Ф=,т. е.

f=1/Ф=R/(2n),

что совпадает с результатом, выраженным формулой (2).

Задачи

Отражение и преломление света

28.1. Два плоских прямоугольных зеркала образуют двугранный угол φ=179°. На расстоянии l=10 см от линии соприкосновения зеркал и на одинаковом расстоянии от каждого зеркала находится точечный источник света. Определить расстояние d между мнимыми изображениями источника в зеркалах.

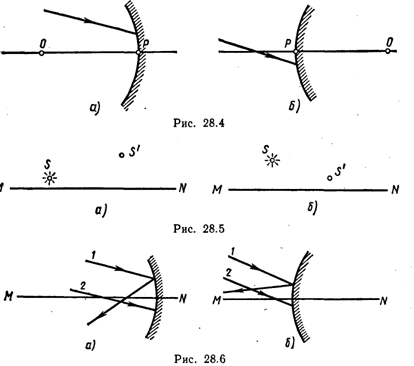
28.2. На сферическое зеркало падает луч света. Найти построе­нием ход луча после отражения в двух случаях: а) от вогнутого зеркала (рис. 28.4, а); б) от выпуклого зеркала (рис. 28.4, б). На рисунке: Р — полюс зеркала; О — оптический центр.

28.3. Вогнутое сферическое зеркало дает на экране изображение предмета, увеличенное в Г=4 раза. Расстояние а от предмета до зеркала равно 25 см. Определить радиус R кривизны зеркала.

28.4. Фокусное расстояние f вогнутого зеркала равна 15 см. Зеркало дает действительное изображение предмета, уменьшенное в три раза. Определить расстояние а от предмета до зеркала.

28.5. На рис. 28.5, а, б указаны положения главной оптической оси MN сферического зеркала, светящейся точки 5 и ее изображе­ния S'. Найти построением положения оптического центра О зер­кала, его полюса Р и главного фокуса F. Определить, вогнутым или выпуклым является данное зеркало. Будет ли изображение действительным или мнимым?

28.6. Вогнутое зеркало дает на экране изображение Солнца в виде кружка диаметром d=28 мм. Диаметр Солнца на небе в угло­вой мере β=32'. Определить радиус R кривизны зеркала.

28.7. Радиус R кривизны выпуклого зеркала равен 50 см. Пред­мет высотой h=15 см находится на расстоянии и, равном 1 м, от зеркала. Определить расстояние b от зеркала до изображения и его высоту Н.

28.8. На рис. 28,6, а, б указаны положения главной оптической оси MN сферического зеркала и ход луча 1. Построить ход луча 2 после отражения его от зеркала.

28.9. На столе лежит лист бумаги. Луч света, падающий на бу­магу под углом ε=30°, дает на ней светлое пятно. Насколько смес­тится это пятно, если на бумагу положить плоскопараллельную стеклянную пластину толщиной d=5 см?

28.10. Луч падает под углом ε=60° на стеклянную пластинку толщиной d=30 мм. Определить боковое смещение Δx; луча после выхода из пластинки.

28.11. Пучок параллельных лучей падает на толстую стеклян­ную пластину под углом ε=60°, и преломляясь переходит в стек­ло. Ширина а пучка в воздухе равна 10 см. Определить ширину b пучка в стекле.

28.12. Луч света переходит из среды с показателем преломления n1 в среду с показателем преломления n2. Показать, что если угол между отраженным и преломленным лучами равен π/2, то выпол­няется условие tgε1==n2/n1 (ε1 — угол падения).

28.13. Луч света падает на грань призмы с показателем прелом­ления п под малым углом. Показать, что если преломляющий угол θ призмы мал, то угол отклонения σ лучей не зависит от угла паде­ния и равен θ(n — 1).

28.14. На стеклянную призму с преломляющим углом θ=60° падает луч света. Определить показатель преломления п стекла, если при симметричном ходе луча в призме угол отклонения σ =40°.

28.15. Преломляющий угол θ стеклянной призмы равен 30°. Луч света падает на грань призмы перпендикулярно ее поверхнос­ти и выходит в воздух из другой грани, отклоняясь на угол σ=20° от первоначального направления. Определить показатель прелом­ления п стекла.

28.16. Луч света падает на грань стеклянной призмы перпенди­кулярно ее поверхности и выходит из противоположной грани, отклонившись на угол σ=25° от первоначального направления. Определить преломляющий угол θ призмы.

28.17. На грань стеклянной призмы с преломляющим углом θ=60° падает луч света под углом ε1=45°. Найти угол преломления ε2’, луча при выходе из призмы и угол отклонения σ луча от перво­начального направления.

28.18. Преломляющий угол θ призмы равен 60°. Угол наимень­шего отклонения луча от первоначального направления σ =30°. Определить показатель преломления п стекла, из которого изготов­лена призма.

28.19. Преломляющий угол θ призмы, имеющей форму острого клина, равен 2°. Определить угол наименьшего отклонения σmin луча при прохождении через призму, если показатель преломления п стекла призмы равен 1,6.

Оптические системы

28.20. На тонкую линзу падает луч света. Найти построением ход луча после преломления его линзой: а) собирающей (рис. 28.7, а); б) рассеивающей (рис. 28,7 б). На рисунке: O — оптический центр линзы; F — главный фокус.

28.21.- На рис. 28.8, а, б, указаны положения главной оптичес­кой оси MN линзы и ход луча 1. Построить * ход луча 2 после пре­ломления его линзой.

28.22. Найти построением положение светящейся точки, если известен ход лучей после преломления их в линзах: а) собираю­щей (рис. 28.9, а); б) рассеивающей (рис. 28.9, б). На рисунке: О — оптический центр линзы; F — ее главный фокус.

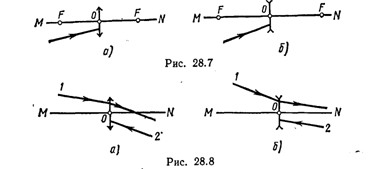
28.23. На рис. 28.10, а, б указаны положения главной оптичес­кой оси MN тонкой линзы, светящейся точки S и ее изображения S'. Найти построением * положения оптического центра О линзы и ее фокусов F. Указать, собирающей или рассеивающей будет дан­ная линза. Будет ли изображение действительным или мнимым?

28.24. Линза, расположенная на оптической скамье между лам­почкой и экраном, дает на экране резко увеличенное изображение лампочки. Когда Лампочку передвинули Δl=40 см ближе к экрану, на нем появилось резко уменьшенное, изображение лампочки. Оп­ределить фокусное расстояние f линзы, если расстояние l от лампоч­ки до экрана равно 80 см.

28.25. Каково наименьшее возможное расстояние l между пред­метом и его действительным изображением, создаваемым собираю­щей линзой с главным фокусным расстоянием f=12 см?

28.26. Человек движется вдоль главной оптической оси объектива фотоаппарата со скоростью v=5 м/с. С какой скоростью и необ­ходимо перемещать матовое стекло фотоаппарата, чтобы изображе­ние человека на нем все время оставалось резким. Главное фокус­ное расстояние f объектива равно 20 см. Вычисления выполнить для случая, когда человек находился на расстоянии а=10 м от фо­тоаппарата.

28.27. Из стекла требуется изготовить плосковыпуклую линзу, оптическая сила Ф которой равна 5 дптр. Определить радиус R кривизны выпуклой поверхности линзы.

28.28. Двояковыпуклая линза имеет одинаковые радиусы кри­визны поверхностей. При каком радиусе кривизны R поверхностей линзы главное фокусное расстояние f ее будет равно 20 см?

28.29. Отношение k радиусов кривизны поверхностей линзы равно 2. При каком радиусе кривизны R. выпуклой поверхности оп­тическая сила Ф линзы равна 10 дптр?

28.30. Определить радиус R кривизны выпуклой поверхности линзы, если при отношении k радиусов кривизны поверхностей линзы, равном 3, ее оптическая сила Ф=-8 дптр.

28.31. Из двух часовых стекол с одинаковыми радиусами R кривизны, равными 0,5 м, склеена двуяковогнутая «воздушная» линза. Какой оптической силой Ф будет обладать такая линза в воде?

28.32. Линза изготовлена из стекла, показатель преломления которого для красных лучей nк=1,50, для фиолетовых nф=1,52. Радиусы кривизны R обеих поверхностей линзы одинаковы и равны 1 м. Определить расстояние Δf между фокусами линзы для красных и фиолетовых лучей.

28.33. Определить главное фокусное расстояние f плосковыпук­лой линзы, диаметр d которой равен 10 см. Толщина h в центре лин­зы равна 1 см, толщину у краев можно принять равной нулю.

28.34. Определить оптическую силу Ф мениска*, если радиусы кривизны R1 и R2 его выпуклой и вогнутой поверхностей равны соответственно 1 м и 40 см.

28.35. Главное фокусное расстояние f собирающей линзы в воз­духе равно 10 см. Определить, чему оно равно: 1) в воде; 2) в корич­ном масле.

28.36. У линзы, находящейся в воздухе, фокусное расстояние f1=5 см, а погруженной в раствор сахара f2=35 см. Определить по­казатель преломления n раствора.

28.37. Тонкая линза, помещенная в воздухе, обладает оптической силой Ф1=5 дптр, а в некоторой жидкости Ф2=-0,48 дптр. Оп­ределить показатель преломления n2 жидкости, если показатель преломления n1 стекла, из которого изготовлена линза, равен 1,52.

28.38. Доказать, что оптическая сила Ф системы двух сложенных

вплотную тонких линз равна сумме оптических сил Ф1 и Ф2 каждой из этих линз.

28.39. В вогнутое сферическое зеркало радиусом R=20 см на­лит тонким слоем глицерин. Определить главное фокусное расстоя­ние f такой системы.

28.40. Плосковыпуклая линза имеет оптическую силу Ф1=4 дптр. Выпуклую поверхность линзы посеребрили. Найти оптичес­кую силу Ф2 такого сферического зеркала.

28.41. Поверх выпуклого сферического зеркала радиусом кри­визны R=20 см налили тонкий слой воды. Определить главное фо­кусное расстояние f такой системы.

28.42. Человек без очков читает книгу, располагая ее перед собой на расстоянии а=12,5 см. Какой оптической силы Ф очки следует ему носить?

28.43. Пределы аккомодации глаза близорукого человека без очков лежат между a1=16 см и a2=80 см. В очках он хорошо видит удаленные предметы. На каком минимальном расстоянии d он может держать книгу при чтении в очках?

28.44. Лупа, представляющая собой двояковыпуклую линзу, изготовлена из стекла с показателем преломления n=1,6. Радиусы кривизны R поверхностей линзы одинаковы и равны 12 см. Опреде­лить увеличение Г лупы.

28.45. Лупа дает увеличение Г=2. Вплотную к ней приложили собирательную линзу с оптической силой Ф1=20 дптр. Какое уве­личение Г2 будет давать такая составная лупа?

28.46. Оптическая сила Ф объектива телескопа равна 0,5 дптр. Окуляр действует как лупа, дающая увеличение Г1=10. Какое увеличение Г2 дает телескоп?

28.47. При окуляре с фокусным расстоянием f=50 мм телескоп дает угловое увеличение Г1==60. Какое угловое увеличение Г2 даст один объектив, если убрать окуляр и рассматривать действи­тельное изображение, созданное объективом, невооруженным гла­зом с расстояния наилучшего зрения?

28.48. Фокусное расстояние f1 объектива телескопа равно 1 м. В телескоп рассматривали здание, находящееся на расстоянии а= 1 км. В каком направлении и на сколько нужно передвинуть окуляр, чтобы получить резкое изображение в двух случаях: 1) если после здания будут рассматривать Луну; 2) если вместо Луны будут рас­сматривать близкие предметы, находящиеся на расстоянии a1= =100 м?

28.49. Телескоп наведен на Солнце. Фокусное расстояние f1 объектива телескопа равно 3 м. Окуляр с фокусным расстоянием f2=50 мм проецирует действительное изображение Солнца, создан­ное объективом, на экран, расположенный на расстоянии b=60 см от окуляра. Плоскость экрана перпендикулярна оптической оси телескопа. Определить линейный диаметр d изображения Солнца на экране, если диаметр Солнца на небе виден невооруженным глазом под углом α=32'.

28.50. Фокусное расстояние f1 объектива микроскопа равно 8 мм, окуляра f2==4 см. Предмет находится на Δа=0,5 мм дальше от объек­тива, чем главный фокус. Определить увеличение Г микроскопа.

28.51. Фокусное расстояние f1 объектива микроскопа равно 1 см, окуляра f2=2 см. Расстояние от объектива до окуляра L=23 см. Какое увеличение Г дает микроскоп? На каком расстоянии а от объектива находится предмет?

28.52. Расстояние δ между фокусами объектива и окуляра внут­ри микроскопа равно 16 см. Фокусное расстояние f1 объектива рав­но 1 мм. С каким фокусным расстоянием f2 следует взять окуляр, чтобы получить увеличение Г=500?

§ 29. ФОТОМЕТРИЯ

Основные формулы

• Световой поток Фv испускаемый изотропным* точечным ис­точником света в пределах телесного угла ω, в вершине которого находится источник, выражается формулой

Фv=Iω,

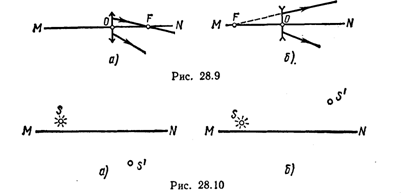
где I — сила света источника; ω=2π(1 — cos); — угол между осью конуса и его образующей.

• Полный световой поток, испускаемый изотропным точечным источником света,

Ф0=4πI.

• Освещенность поверхности определяется соотношением

Ev=Ф/S,

где S — площадь поверхности, по которой равномерно распределя­ется падающий на нее световой поток Фv.

Освещенность, создаваемая изотропным точечным источником света,

Ev =,

где r — расстояние от поверхности до источника света; ε — угол падения лучей.

• Сила света любого элемента поверхности косинусного излуча­теля

I=I0cosφ,

где φ — угол между нормалью к элементу поверхности и направ­лением наблюдения; I0 — сила света элемента поверхности по на­правлению нормали к этому элементу.

• Яркость светящейся поверхности

Lv=I/σ, где I — сила света в направлении наблюдения; σ — площадь про­екции светящейся поверхности на плоскость, перпендикулярную этому направлению.

• Светимость определяется соотношением

Mv=Фv/S,

где Фv — световой поток, испускаемый поверхностью; S — пло­щадь этой поверхности.

Светимость косинусных излучателей

Мv=πLv.

Примечание. В соответствии с ГОСТ 26148—84 световые величины обо­значаются теми же буквами, что и соответствующие им энергетические вели­чины излучений. Отличаются обозначения только индексами: е — для энер­гетических величин и v — для световых. Но в обозначениях световых величин индекс v разрешается опускать в тех случаях, когда это не может привести к недоразумениям (например, энергетическая яркость — Le яркость — Lv или L).

Примеры решения задач

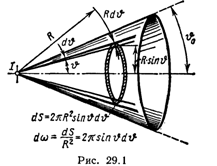
Пример 1. Прожектор ближнего освещения дает пучок света в виде усеченного конуса с углом раствора 2=40°. Световой поток Ф прожектора равен 80 клм. Допуская, что световой поток распре­делен внутри конуса равномерно, определить силу света I прожек­тора.

Решение. Сила света I изотропного источника равна отно­шению светового потока Ф к телесному углу ω, в пределах которо­го распространяется световой поток, т. е.

I=Ф/ω. (1)

Выразим телесный угол через угол раствора. Из рис. 29.1 сле­дует, что элементарный телесный угол dω =2πsind. Телесный угол, соответствующий углу раствора 2 конуса, выразится интегралом:

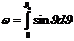, или

ω=2π(1 — cos) = 4 πsin2 (/2).

Подставив выражение ω в формулу (1), получим

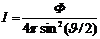. (2)

Произведя вычисления по формуле (2), найдем I==211 ккд.

Пример 2. Люминесцентная цилиндрическая лампа диаметром d=2,5 см и длиной l=40 см создает на расстоянии r=5 м в направ­лении, перпендикулярном оси лампы, освещенность Еv=2 лк. При­нимая лампу за косинусный излучатель, определить; 1) силу света I в данном направлении; 2) яркость L; 3) светимость М лампы.

Решение. 1. Больший из двух размеров лампы — длина — в 12 раз меньше расстояния, на котором измерена освещенность.

Следовательно, для вычисления силы света в данном направлении можно принять лампу за точечный источник и применить формулу

E=I/r2, откуда I=Er2.

Подставив значения величин в эту формулу и произведя вычис­ления, получим

I=25 кд.

2. Для вычисления яркости применим формулу

L=I/σ,

где а — площадь проекции протяженного источника света на плос­кость, перпендикулярную направлению наблюдения.

В случае цилиндрической люминесцентной лампы проекция име­ет форму прямоугольника длиной / и шириной d. Следовательно,

L=I/(ld).

Произведя вычисления по этой формуле, найдем

L=2,5 ккд/м2.

3. Так как люминесцентную лампу можно считать косинусным излучателем, то ее светимость

М=πL=7,9 клк.

Задачи*

Световой поток, и сила света

29.1. Определить силу света I точечного источника, полный све­товой поток Ф которого равен 1 лм.

29.2. Лампочка, потребляющая мощность Р=75 Вт, создает на расстоянии r=3 м при нормальном падении лучей освещенность E=8 лк. Определить удельную мощность р лампочки (в ваттах на канделу) и световую отдачу η лампочки (в люменах на ватт).

29.3. В вершине кругового конуса находится точечный источник света, посылающий внутри конуса световой поток Ф==76 лм. Сила света I источника равна 120 кд. Определить телесный угол ω и угол раствора 2 конуса.

29.4. Какую силу тока I покажет гальванометр, присоединен­ный к селеновому фотоэлементу, если на расстоянии r=75 см от него поместить лампочку, полный световой поток Ф0 которой ра­вен 1,2 клм? Площадь рабочей поверхности фотоэлемента равна 10 см2, чувствительность i=300 мкА/лм.

Освещенность

29.5. Лампочка силой света I=80 кд находится на расстоянии а=2 м от собирательной линзы с диаметром d=12 см и главным фокусным расстоянием f=40 см. Линза дает на экране, расположенном на расстоянии b=30 см от линзы, круглое светлое пятно. Найти освещенность Е экрана на месте этого пятна. Поглощением света в линзе пренебречь.

29.6. При печатании фотоснимка негатив освещался в течение t1=3 с лампочкой силой света I1==15 кд с расстояния r1=50 см. Определить время t2, в течение которого нужно освещать негатив лампочкой силой света I2=60 кд с расстояния r2==2 м, чтобы полу­чить отпечаток с такой же степенью почернения, как и в первом случае?

29.7. На высоте h=3 м над землей и на расстоянии r=4 м от сте­ны висит лампа силой света I=100 кд. Определить освещенность Е1 стены и Е2 горизонтальной поверхности земли у линии их пересе­чения.

29.8. На мачте высотой h=8 м висит лампа силой света I=1 ккд. Принимая лампу за точечный источник света, определить, на ка­ком расстоянии l от основания мачты освещенность Е поверхности земли равна 1 лк.

29.9. Над центром круглой площадки висит лампа. Освещенность E1 в центре площадки равна 40 лк, Е2 на краю площадки равна 5 лк. Под каким углом в падают лучи на край площадки?

29.10. Над центром круглого стола радиусом r=80 см на высоте h=60 см висит лампа силой света I=100 кд. Определить: 1) осве­щенность E1 в центре стола; 2) освещенность E2 на краю стола; 3) световой поток Ф, падающий на стол; 4) среднюю освещенность <E> стола.

29.11. На какой высоте h над центром круглого стола радиу­сом г=\ м нужно повесить лампочку, чтобы освещенность на краю стола была максимальной?

Яркость и светимость

29.12. Отверстие в корпусе фонаря закрыто плоским молочным стеклом размером 10х15 см. Сила света I фонаря в направлении, составляющем угол φ=60° с нормалью, равна 15 кд. Определить яркость L стекла.

29.13. Вычислить и сравнить между собой силы света раскален­ного металлического шарика яркостью L1=3 Мкд/м2 и шарового светильника яркостью L2=5 ккд/м2, если их диаметры d1 и d2 со­ответственно равны 2 мм и 20 см.

29.14. Светильник из молочного стекла имеет форму шара диа­метром d=20 см. Сила света I шара равна 80 кд. Определить пол­ный световой поток Ф, светимость М и яркость L светильника.

29.15. Солнце, находясь вблизи зенита, создает на горизонталь­ной поверхности освещенность E=0,1 Млк. Диаметр Солнца виден под углом α =32'. Определить видимую яркость L Солнца.

29.16. Длина l раскаленной добела металлической нити равна 30 см, диаметр d=0,2 мм. Сила света I нити в перпендикулярном ей направлении равна 24 кд. Определить яркость L нити.

29.17. Яркость L светящегося куба одинакова во всех направле­ниях и равна 5 ккд/м2. Ребро а куба равно 20 см. В каком направ­лении сила света I куба максимальна? Определить максимальную силу света Imах куба.

29.18. Светящийся конус имеет одинаковую во всех направле­ниях яркость B=2 ккд/м2. Основание конуса не светится. Диаметр d основания равен 20 см, высота h=15 см. Определить силу света I конуса в направлениях: 1) вдоль оси; 2) перпендикулярном оси.

29.19. На высоте h=1 м над горизонтальной плоскостью парал­лельно ей расположен небольшой светящийся диск. Сила света I0 диска в направлении его оси равна 100 кд. Принимая диск за то­чечный источник с косинусным распределением силы света, найти освещенность Е горизонтальной плоскости в точке А, удаленной на расстояние r=3 м от точки, расположенной под центром диска.

29.20. На какой высоте h над горизонтальной плоскостью (см. предыдущую задачу) нужно поместить светящийся диск, чтобы осве­щенность в точке А была максимальной?

29.21. Определить освещенность Е, светимость М и яркость L киноэкрана, равномерно рассеивающего свет во всех направлениях, если световой поток Ф, падающий на экран из объектива киноаппа­рата (без киноленты), равен 1,75 клм. Размер экрана 5х3,6 м, ко­эффициент отражения ρ=0,75.

29.22. На какой высоте h нужно повесить лампочку силой све­та I=10 кд над листом матовой белой бумаги, чтобы яркость L бу­маги была равна 1 кд/м2, если коэффициент отражения ρ бумаги равен 0,8?

29.23. Освещенность Е поверхности, покрытой слоем сажи, рав­на 150 лк, яркость L одинакова во всех направлениях и равна 1 кд/м2. Определить коэффициент отражения ρ сажи.

§ 30. ИНТЕРФЕРЕНЦИЯ СВЕТА

Основные формулы

• Скорость света в среде

v=c/n,

где с — скорость света в вакууме; п — абсолютный показатель преломления среды.

• Оптическая длина пути световой волны

L=nl,

где l — геометрическая длина пути световой волны в среде с пока­зателем преломления п.

3. Оптическая разность хода двух световых волн

Δ=L1—L2.

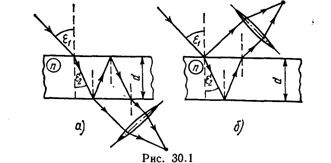
• Оптическая разность хода световых волн, отраженных от верхней и нижней поверхностей тонкой плоскопараллельной пластинки или пленки, находящейся в воздухе (рис. 30.1, а),

Δ=, или Δ=2dn cos ε2’ + λ/2, где d — толщина пластинки (пленки); ε1 — угол падения; ε2’ -— угол преломления.

Второе слагаемое в этих формулах учитывает изменение опти­ческой длины пути световой волны на λ/2 при отражении ее от сре­ды оптически более плотной.

В проходящем свете (рис. 30.1, б) отражение световой волны происходит от среды оптически менее плотной и дополнительной разности хода световых лучей не возникает.

• Связь разности фаз Δφ колебаний с оптической разностью хо­да волн

Δφ=2πΔ/λ..

• Условие максимумов интенсивности света при интерферен­ции

Δ=±kλ (k=0,l,2,3, …).

• Условие минимумов интенсивности света при интерферен­ции

Δ=±(2k+1) (λ/2).

• Радиусы светлых колец Ньютона в отраженном свете (или темных в проходящем)

rk=.

где k — номер кольца (k=1, 2, 3, …); R — радиус кривизны по­верхности линзы, соприкасающейся с плоскопараллельной стек­лянной пластинкой.

Радиусы темных колец в отраженном свете (или светлых в про­ходящем)

.

Примеры решения задач

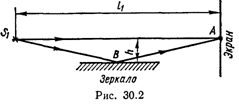
Пример 1. В точку А экрана от источника S1 монохроматическо­го света длиной волны λ=0,5мкм приходят два луча: непосредствен­но от источника луч S1A, перпендикулярный экрану, и луч S1BA,отраженный в точке В от зеркала, параллельного лучу S1A (рис. 30.2). Расстояние l1 экрана от источника равно 1 м, расстояние h от луча S1A до плоскости зеркала равно 2 мм. Определить: 1) что будет наблюдаться в точке А экрана — усиление или ослабление интенсивности; 2) как изменится интенсивность в точке А, если на пути луча S1A перпенди­кулярно ему поместить плоскопараллельную пластинку стекла (n=1,55) толщиной d=6 мкм.

Решение. Пост­роим мнимое изобра­жение S2 источника S1 в зеркале (рис. 30.3). Источники S1 и S2 являются когерентными, поэтому при сложении волн, приходящих от этих источников на экран, возникает интерференционная картина. Усиление или ос­лабление интенсивности в той или иной точке экрана зависит от оптической разности хода Δ интерферирующих лучей, другими сло­вами, от числа т полуволн, укладывающихся на оптической раз­ности хода:

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3