![]() (1)
(1)
Если т — целое четное, то интенсивность будет максимальной; если т — целое нечетное, то интенсивность минимальна. При дробном т происходит или частичное усиление (если т ближе к четному числу), или частичное ослабление (если т ближе к нечетному числу). 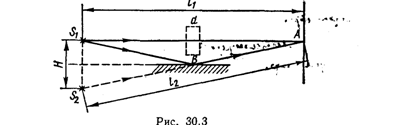
1. Оптическая разность хода Δ1 будет складываться из геометрической разности l2—l1 (оба луча идут в воздухе) и дополнительной разности хода λ/2, обусловленной изменением фазы колебаний на π при отражении от среды оптически более плотной. Таким образом,
Δ1=l2—l1+ λ/2. (2)
Так как l2=![]() (рис. 30.3), то
(рис. 30.3), то
l2—l1=![]() .
.
Величина H/l1<<1, поэтому для вычисления корня можно воспользоваться приближенной формулой (см. табл. 3) ![]()
при а<<1. Применив ее, получим
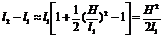 .
.
Подставив полученное выражение l2—l1 в формулу (2), найдем
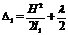 . Зная Δ1, по формуле (1) найдем m1:
. Зная Δ1, по формуле (1) найдем m1:
![]() .
.
Так как Н=2h, то окончательно получим
![]() .
.
После вычисления найдем
m1=33.
Так как на разности хода укладывается нечетное число длин полуволн, то в точке А наблюдается минимум интенсивности.
2. Стеклянная пластина толщиной d, поставленная на пути луча S1A (рис. 30.3), изменит оптическую длину пути. Теперь оптическая длина пути L будет складываться из геометрической длины пути l1—d и оптической длины пути nd луча в самой пластине, т. е.
L= (l1—d)+nd==l1+ (n—1)d.
Оптическая разность хода лучей
Δ2=l2—L+λ/2=l2—[l1 + (n—l)d]+λ/2, или
Δ2= Δ1—(n—1)d.
Пользуясь формулой (1), найдем
![]() .
.
Произведя вычисления, получим m2=19,8.
Число длин полуволн оказалось дробным. Так как 19,8 ближе к целому четному числу 20, чем к целому нечетному числу 19, то в точке А будет частичное усиление.
|
Пример 2. На толстую стеклянную пластинку, покрытую очень тонкой пленкой, показатель преломления n2 вещества которой равен 1,4, падает нормально параллельный пучок монохроматического света (λ=0,6 мкм). Отраженный свет максимально ослаблен вследствие интерференции. Определить толщину d пленки.
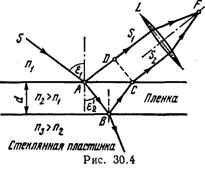
Решение. Из световой волны, падающей на пленку, выделим узкий пучок SA. Ход этого пучка в случае, когда угол падения ε1 0, показан на рис. 30.4. В точках A и В падающий пучок частично отражается и частично преломляется. Отраженные пучки света AS1 и BCS1 падают на собирающую линзу L, пересекаются в ее фокусе F и интерферируют между собой.
Так как показатель преломления воздуха (n1= 1,00029) меньше показателя преломления вещества пленки (n2=1,4), который, в свою очередь, меньше показателя преломления стекла (n3=1,5), то в обоих случаях отражение происходит от среды оптически более плотной, чем та среда, в которой идет падающая волна. Поэтому фаза колебания пучка света AS1 при отражении в точке A изменяется на π рад и точно так же на π рад изменяется фаза колебаний пучка света BCS2 при отражении в точке В. Следовательно, результат интерференции этих пучков света при пересечении в фокусе F линзы будет такой же, как если бы никакого изменения фазы колебаний ни у того, ни у другого пучка не было.
Как известно, условие максимального ослабления света при интерференции в тонких пленках состоит в том, что оптическая разность хода Δ интерферирующих волн должна быть равна нечетному числу полуволн; Δ=(2k+1)(λ/2).
Как видно из рис. 30.4, оптическая разность хода
Δ=l2n2— l1n1=(|АВ| +|ВС|) п2—|AD| n1.
Следовательно, условие минимума интенсивность света примет вид
(|АВ| +|ВС|) п2—|AD| n1=(2k+1)(λ/2).
Если угол падения ε1 будет уменьшаться, стремясь к нулю, то AD 0 и (|АВ|+|ВС|![]() 2d, где d—толщина пленки. В пределе при ε1=0 будем иметь
2d, где d—толщина пленки. В пределе при ε1=0 будем иметь
Δ=2dn2=(2k+1)(λ /2),
откуда искомая толщина пленки
![]() .
.
Полагая k=0,1,2,3,…, получим ряд возможных значений толщины пленки:
![]()
![]() и т. д.
и т. д.
Пример 3. На стеклянный клин нормально к его грани падает монохроматический свет с длиной волны λ=0,6 мкм. В возникшей при этом интерференционной картине на отрезке длиной l=1 см наблюдается 10 полос. Определить преломляющий угол θ клина.
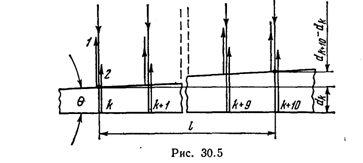
Решение. Параллельный пучок света, падая нормально к грани клина, отражается как от верхней, так и от нижней грани. Эти пучки когерентны, и поэтому наблюдается устойчивая картина интерференции. Так как интерференционные полосы наблюдаются при малых углах клина, то отраженные пучки света 1 и 2 (рис. 30.5) будут практически параллельны.
Темные полосы видны на тех участках клина, для которых разность хода кратна нечетному числу половины длины волны;
Δ=(2k+1) (λ/2), где k=0,1,2,…. (1)
Разность хода Δ двух волн складывается из разности оптических длин путей этих волн (2dn cosε2’) и половины длины волны (λ/2).
Величина λ/2 представляет собой добавочную разность хода, возникающую при отражении волны от оптически более плотной среды. Подставляя в формулу (1) значение разности хода Δ, получим
2dkn cos ε2’ + λ/2 = (2k + 1) (λ/2), (2)
где п — коэффициент преломления стекла (n=l,5); dk—толщина клина в том месте, где наблюдается темная полоса, соответствующая номеру k; ε2’—угол преломления.
Согласно условию, угол падения равен нулю, следовательно, и угол преломления ε2’ равен нулю, a cos ε2’=1. Раскрыв скобки в правой части равенства (2), после упрощения получим
2dkn=kλ (3)
Пусть произвольной темной полосе номера k соответствует определенная толщина клина в этом месте dk а темной полосе номера k+10 соответствует толщина клина dk+10. Согласно условию задачи, 10 полос укладываются на отрезке длиной l=1 см. Тогда искомый угол (рис. 30.5) будет равен
θ=(dk+10 – dk)/l, (4)
где из-за малости преломляющего угла sin θ=θ (угол θ выражен в радианах).
Вычислив dk и dk+10 из формулы (3), подставив их в формулу (4) и произведя преобразования, найдем
θ=5λ/(nl).
После вычисления получим
θ=2*10-4paд.
Выразим θ в градусах. Для этого воспользуемся соотношением между радианом и секундой (см. табл. 6); 1 рад=2,06"*105, т. е.
θ=2*10-4*2,06''*105=41,2'',
или в соответствии с общим правилом перевода из радиан в градусы
θград =![]() θрад, θ=
θрад, θ=![]() .
.
Искомый угол равен 41,2".
Задачи
Интерференция волн от двух когерентных источников
30.1. Сколько длин волн монохроматического света с частотой колебаний υ=5*1014 Гц уложится на пути длиной l=1,2 мм: 1) в вакууме; 2) в стекле?
30.2. Определить длину l1 отрезка, на котором укладывается столько же длин волн в вакууме, сколько их укладывается на отрезке l2=3 мм в воде.
30.3. Какой длины l1 путь пройдет фронт волны монохроматического света в вакууме за то же время, за какое он проходит путь длиной l2=1 м в воде?
30.4. На пути световой волны, идущей в воздухе, поставили стеклянную пластинку толщиной h=1 мм. На сколько изменится оптическая длина пути, если волна падает на пластинку: 1) нормально; 2) под углом ε=30°?
30.5. На пути монохроматического света с длиной волны λ=0,6 мкм находится плоскопараллельная стеклянная пластина толщиной d=0,l мм. Свет падает на пластину нормально. На какой угол φ следует повернуть пластину, чтобы оптическая длина пути L изменилась на λ/2?
|
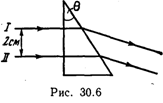
30.6. Два параллельных пучка световых волн I и II падают на стеклянную призму с преломляющим углом θ=30° и после преломления выходят из нее (рис. 30.6). Найти оптическую разность хода Δ световых волн после преломления их призмой.
30.7. Оптическая разность хода Δ двух интерферирующих волн монохроматического света равна 0,3λ. Определить разность фаз Δφ.
30.8. Найти все длины волн видимого света (от 0,76 до 0,38 мкм), которые будут: 1) максимально усилены; 2) максимально ослаблены при оптической разности хода Δ интерферирующих волн, равной 1,8 мкм.
30.9. Расстояние d между двумя когерентными источниками света (λ=0,5 мкм) равно 0,1 мм. Расстояние b между интерференционными полосами на экране в средней части интерференционной картины равно 1 см. Определить расстояние l от источников до экрана.
30,10. Расстояние d между двумя щелями в опыте Юнга равно 1мм, расстояние l от щелей до экрана равно 3 м. Определить длину
волны λ, испускаемой источником монохроматического света, если ширина b полос интерференции на экране равна 1,5 мм.
30.11. В опыте Юнга расстояние d между щелями равно 0,8 мм. На каком расстоянии l от щелей следует расположить экран, чтобы ширина b интерференционной полосы оказалась равной 2 мм?
|
30.12. В опыте с зеркалами Френеля расстояние d между мнимыми изображениями источника света равно 0,5 мм, расстояние l от них до экрана равно 3 м. Длина волны λ=0,6 мкм. Определить ширину b полос интерференции на экране.
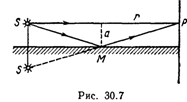
30.13. Источник S света (λ=0,6 мкм) и плоское зеркало М расположены, как показано на рис. 30.7 (зеркало Ллойда). Что будет наблюдаться в точке Р экрана, где сходятся лучи SP и SMP,— свет или темнота, если |SP|=r=2 м, a=0,55 мм, |SM|=|MP|?
Интерференция света в тонких пленках
30.14. При некотором расположении зеркала Ллойда ширина b интерференционной полосы на экране оказалась равной 1 мм. После того как зеркало сместили параллельно самому себе на расстояние Δd=0,3 мм, ширина интерференционной полосы изменилась. В каком направлении и на какое расстояние Δl следует переместить экран, чтобы ширина интерференционной полосы осталась прежней? Длина волны λ монохроматического света равна 0,6 мкм.
|
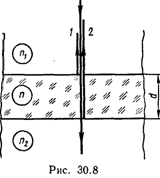
30.15. Плоскопараллельная стеклянная пластинка толщиной d=1,2 мкм и показателем преломления n=1,5 помещена между двумя средами с показателями преломления n1 и n2 (рис. 30.8). Свет с длиной волны λ=0,6 мкм падает нормально на пластинку. Определить оптическую разность хода Δ волн 1 и 2, отраженных от верхней и нижней поверхностей пластинки, и указать, усиление или ослабление интенсивности света происходит при интерференции в следующих случаях: 1) n1<.п<n2; 2) n1>n>n2; 3) п1<п>п2; 4) n1>n<n2.
30.16. На мыльную пленку (n=1,3), находящуюся в воздухе, падает нормально пучок лучей белого света. При какой наименьшей толщине d пленки отраженный свет с длиной волны λ=0,55 мкм окажется максимально усиленным в результате интерференции?
30.17. Пучок монохроматических (λ=0,6 мкм) световых волн падает под углом ε1=30° на находящуюся в воздухе мыльную пленку (n=1,3). При какой наименьшей толщине d пленки отраженные световые волны будут максимально ослаблены интерференцией? максимально усилены?
30.18. На тонкий стеклянный клин (n=1,55) падает нормально монохроматический свет. Двугранный угол α между поверхностями клина равен 2'. Определить длину световой волны λ, если расстояние b между смежными интерференционными максимумами в отраженном свете равно 0,3 мм.
30.19. Поверхности стеклянного клина образуют между собой угол θ=0,2'. На клин нормально к его поверхности падает пучок лучей монохроматического света с длиной волны λ=0,55 мкм. Определить ширину b интерференционной полосы.
30.20. На тонкий стеклянный клин в направлении нормали к его поверхности падает монохроматический свет (λ=600 нм). Определить угол θ между поверхностями клина, если расстояние b между смежными интерференционными минимумами в отраженном свете равно 4 мм.
30.21. Между двумя плоскопараллельными стеклянными пластинками положили очень тонкую проволочку, расположенную параллельно линии соприкосновения пластинок и находящуюся на расстоянии l=75 мм от нее. В отраженном свете (λ=0,5 мкм) на верхней пластинке видны интерференционные полосы. Определить диаметр d поперечного сечения проволочки, если на протяжении а=30 мм насчитывается m=16 светлых полос.
30.22. Две плоскопараллельные стеклянные пластинки приложены одна к другой так, что между ними образовался воздушный клин с углом θ, равным 30". На одну из пластинок падает нормально монохроматический свет (λ=0,6 мкм). На каких расстояниях l1 и l2 от линии соприкосновения пластинок будут наблюдаться в отраженном свете первая и вторая светлые полосы (интерференционные максимумы)?
30.23. Две плоскопараллельные стеклянные пластинки образуют клин с углом θ=30'. Пространство между пластинками заполнено глицерином. На клин нормально к его поверхности падает пучок монохроматического света с длиной волны λ=500 нм. В отраженном свете наблюдается интерференционная картина. Какое число N темных интерференционных полос приходится на 1 см длины клина?
30.24. Расстояние Δr2,1 между вторым и первым темным кольцами Ньютона в отраженном свете равно 1 мм. Определить расстояние Δr10,9 между десятым и девятым кольцами.
30.25. Плосковыпуклая линза выпуклой стороной лежит на стеклянной пластинке. Определить толщину d слоя воздуха там, где в отраженном свете (λ=0,6 мкм) видно первое светлое кольцо Ньютона.
30.26. Диаметр d2 второго светлого кольца Ньютона при наблюдении в отраженном свете (λ=0,6 мкм) равен 1,2 мм. Определить оптическую силу D плосковыпуклой линзы, взятой для опыта.
30.27. Плосковыпуклая линза с оптической силой Ф=2 дптр выпуклой стороной лежит на стеклянной пластинке. Радиус r, четвертого темного кольца Ньютона в проходящем свете равен 0,7 мм. Определить длину световой волны.
30.28. Диаметры di и dk двух светлых колец Ньютона соответственно равны 4,0 и 4,8 мм. Порядковые номера колец не определялись, но известно, что между двумя измеренными кольцами расположено три светлых кольца. Кольца наблюдались в отраженном свете (λ=500 нм). Найти радиус кривизны плосковыпуклой линзы, взятой для опыта.
30.29. Между стеклянной пластинкой и лежащей на ней плосковыпуклой стеклянной линзой налита жидкость, показатель преломления которой меньше показателя преломления стекла. Радиус r8 восьмого темного кольца Ньютона при наблюдении в отраженном свете (λ=700 нм) равен 2 мм. Радиус R кривизны выпуклой поверхности линзы равен 1 м. Найти показатель преломления n жидкости.
30.30. На установке для наблюдения колец Ньютона был измерен в отраженном свете радиус третьего темного кольца (k=3). Когда пространство между плоскопараллельной пластиной и линзой заполнили жидкостью, то тот же радиус стало иметь кольцо с номером, на единицу большим. Определить показатель преломления п жидкости.
30.31. В установке для наблюдения колец Ньютона свет с длиной волны λ=0,5 мкм падает нормально на плосковыпуклую линзу с радиусом кривизны R1=1 м, положенную выпуклой стороной на вогнутую поверхность плосковогнутой линзы с радиусом кривизны R2=2 м. Определить радиус r3 третьего темного кольца Ньютона, наблюдаемого в отраженном свете.
30.32. Кольца Ньютона наблюдаются с помощью двух одинаковых плосковыпуклых линз радиусом R кривизны равным 1м, сложенных вплотную выпуклыми поверхностями (плоские поверхности линз параллельны). Определить радиус r2 второго светлого кольца, наблюдаемого в отраженном свете (λ=660 нм) при нормальном падении света на поверхность верхней линзы.
Интерференционные приборы
30.33. На экране наблюдается интерференционная картина от двух когерентных источников света с длиной волны λ=480 нм. Когда на пути одного из пучков поместили тонкую пластинку из плавленого кварца с показателем преломления n=1,46, то интерференционная картина сместилась на m=69 полос. Определить толщину d кварцевой пластинки.
30.34. В оба пучка света интерферометра Жамена были помещены цилиндрические трубки длиной l=10 см, закрытые с обоих концов плоскопараллельными прозрачными пластинками; воздух из трубок был откачан. При этом наблюдалась интерференционная картина в виде светлых и темных полос. В одну из трубок был впущен водород, после чего интерференционная картина сместилась на m=23,7 полосы. Найти показатель преломления п водорода. Длина волны λ света равна 590 нм.
30.35. В интерферометре Жамена две одинаковые трубки длиной l=15 см были заполнены воздухом. Показатель преломления n1 воздуха равен 1,000292. Когда в одной из трубок воздух заменили ацетиленом, то интерференционная картина сместилась на m=80 полос. Определить показатель преломления n2 ацетилена, если в интерферометре использовался источник монохроматического света с длиной волны λ=0,590 мкм.
30.36. Определить перемещение зеркала в интерферометре Майкельсона, если интерференционная картина сместилась на т=100 полос. Опыт проводился со светом с длиной волны λ=546 нм.
30.37. Для измерения показателя преломления аргона в одно из плеч интерферометра Майкельсона поместили пустую стеклянную трубку длиной l=12 см с плоскопараллельными торцовыми поверхностями. При заполнении трубки аргоном (при нормальные условиях) интерференционная картина сместилась на m=106 полос. Определить показатель преломления п аргона, если длина волны λ света равна 639 нм.
30.38. В интерферометре Майкельсона на пути одного из интерферирующих пучков света (λ=590 нм) поместили закрытую с обеих сторон стеклянную трубку длиной l=10 см, откачанную до высокого вакуума. При заполнении трубки хлористым водородом произошло смещение интерференционной картины. Когда хлористый водород был заменен бромистым водородом, смещение интерференционной картины возросло на Δm=42 полосы. Определить разность Δn показателей преломления бромистого и хлористого водорода.
§ 31. ДИФРАКЦИЯ СВЕТА
Основные формулы
• Радиус k-ой. зоны Френеля:
для сферической волны
![]() ,
,
где а — расстояние диафрагмы с круглым отверстием от точечного источника света; b — расстояние диафрагмы от экрана, на котором ведется наблюдение дифракционной картины; k — номер зоны Френеля; λ — длина волны;
для плоской волны
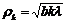 .
.
• Дифракция света на одной щели при нормальном падении лучей. Условие минимумов интенсивности света
![]() , k=1,2,3,…,
, k=1,2,3,…,
где а — ширина щели; φ— угол дифракции; k — номер минимума;
λ — длина волны.
Условие максимумов интенсивности света
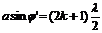 , k=l, 2, 3,…,
, k=l, 2, 3,…,
где φ' — приближенное значение угла дифракции.
• Дифракция света на дифракционной решетке при нормальном падении лучей. Условие главных максимумов интенсивности
d sinφ=±kλ, k=0,1,2,3,…,
где d — период (постоянная) решетки; k — номер главного максимума; φ —угол между нормалью к поверхности решетки и направлением дифрагированных волн.
• Разрешающая сила дифракционной решетки
![]() ,
,
где Δλ — наименьшая разность длин волн двух соседних спектральных линий (λ и λ+Δλ), при которой эти линии могут быть видны раздельно в спектре, полученном посредством данной решетки; N — число штрихов решетки; k — порядковый номер дифракционного максимума.
• Угловая дисперсия дифракционной решетки
![]() ,
,
линейная дисперсия дифракционной решетки
![]() .
.
Для малых углов дифракции
![]() ,
,
где f — главное фокусное расстояние линзы, собирающей на экране дифрагирующие волны.
• Разрешающая сила объектива телескопа
![]() ,
,
где β — наименьшее угловое расстояние между двумя светлыми точками, при котором изображения этих точек в фокальной плоскости объектива могут быть видны раздельно; D — диаметр объектива; λ — длина волны.
• формула Вульфа — Брэгга
2d sin ![]() =kλ,
=kλ,
где d — расстояние между атомными плоскостями кристалла; ![]() — угол скольжения (угол между направлением пучка параллельных лучей, падающих на кристалл, и гранью кристалла), определяющий направление, в котором имеет место зеркальное отражение лучей (дифракционный максимум).
— угол скольжения (угол между направлением пучка параллельных лучей, падающих на кристалл, и гранью кристалла), определяющий направление, в котором имеет место зеркальное отражение лучей (дифракционный максимум).
Примеры решения задач
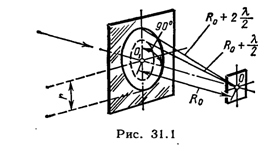
Пример 1. На диафрагму с круглым отверстием радиусом r=1 мм падает нормально параллельный пучок света длиной волны λ=0,05 мкм. На пути лучей, прошедших через отверстие, помещают экран. Определить максимальное расстояние bmax от центра отверстия до экрана, при котором в центре дифракционной картины еще будет наблюдаться темное пятно.
|
Решение. Расстояние, при котором будет видно темное пятно, определяется числом зон Френеля, укладывающихся в отверстии. Если число зон четное, то в центре дифракционной картины будет темное пятно.
Число зон Френеля, помещающихся в отверстии, убывает по мере удаления экрана от отверстия. Наименьшее четное число зон равно двум. Следовательно, максимальное расстояние, при котором еще будет наблюдаться темное пятно в центре экрана, определяется условием, согласно которому в отверстии должны поместиться две зоны Френеля.
Из рис. 31.1 следует, что расстояние от точки наблюдения O на экране до края отверстия на 2 (λ/2) больше, чем расстояние bmax.
По теореме Пифагора получим
![]() .
.
Учтя, что λ<<bmах и что членом, содержащим λ2, можно пренебречь, последнее равенство перепишем в виде
r2=2λbmax. откуда bmax=r2/(2λ). Произведя вычисления по последней формуле, найдем
bmax=1 м.
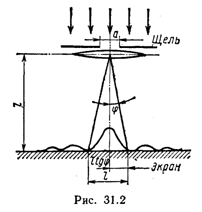
Пример 2. На щель шириной а=0,1 мм нормально падает параллельный пучок света от монохроматического источника (λ==0,6 мкм). Определить ширину l центрального максимума в дифракционной картине, проецируемой с помощью линзы, находящейся непосредственно за щелью, на экран, отстоящий от линзы на расстоянии L=l м.
Решение. Центральный максимум интенсивности света занимает область между ближайшими от него справа и слева минимумами интенсивности. Поэтому ширину центрального максимума интенсивности примем равной расстоянию между этими двумя минимумами интенсивности (рис. 31.2).
Минимумы интенсивности света при дифракции от одной щели наблюдаются под углами φ, определяемыми условием
a sin φ=±kλ, (1)
где k — порядок минимума; в нашем случае равен единице.
Расстояние между двумя минимумами на экране определим непосредственно по чертежу: l=2L tgφ. Заметив, что при малых углах tg φ![]() sin φ, перепишем эту формулу в виде
sin φ, перепишем эту формулу в виде
|
/=2L sin φ. (2)
Выразим sin φ из формулы (1) и подставим его в равенство (2):
l=2Lkλ/a. (3)
Произведя вычисления по формуле (3), получим l=1,2 см.
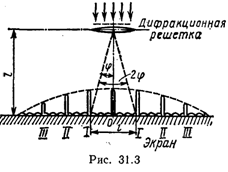
Пример 3. На дифракционную решетку нормально к ее поверхности падает параллельный пучок света с длиной волны λ=0,5мкм. Помещенная вблизи решетки линза проецирует дифракционную картину на плоский экран, удаленный от линзы на L=l м. Расстояние l между двумя максимумами интенсивности первого порядка, наблюдаемыми на экране, равно 20,2 см (рис. 31.3). Определить: 1) постоянную d дифракционной решетки; 2) число n штрихов на 1 см; 3) число максимумов, которое при этом дает дифракционная решетка; 4) максимальный угол φmах отклонения лучей, соответствующих последнему дифракционному максимуму.
Решение 1. Постоянная d дифракционной решетки, длина волны λ и угол φ отклонения лучей, соответствующий k-му дифракционному максимуму, связаны соотношением
|
dsin φ=kλ, (1)
где k — порядок спектра, или в случае монохроматического света порядок максимума.
В данном случае k=1, sin φ=tg φ (ввиду того, что l/2<<L), tgφ=(l/2)L (следует из рис. 31.3). С учетом последних трех равенств соотношение (1) примет вид
![]() ,
,
откуда постоянная решетки
d=2Lλ/l.
Подставляя данные, получим
d=4,95 мкм.
2. Число штрихов на 1 см найдем из формулы
п=1/d.
После подстановки числовых значений получим n=2,02-103 см-1.
3. Для определения числа максимумов, даваемых дифракционной решеткой, вычислим сначала максимальное значение kmax исходя из того, что максимальный угол отклонения лучей решеткой не может превышать 90°.
Из формулы (1) запишем
![]() . (2)
. (2)
Подставляя сюда значения величин, получим
Kmax =9,9.
Число k обязательно должно быть целым. В то же время оно не может принять значение, равное 10, так как при этом значении sin φ должен быть больше единицы, что невозможно. Следовательно, kmах=9.
Определим общее число максимумов дифракционной картины, полученной посредством дифракционной решетки. Влево и вправо от центрального максимума будет наблюдаться по одинаковому числу максимумов, равному kmах, т. е. всего 2kmах. Если учесть также центральный нулевой максимум, получим общее число максимумов
N=2kmax+l.
Подставляя значение kmах найдем
N=2*9+1=19.
4. Для определения максимального угла отклонения лучей, соответствующего последнему дифракционному максимуму, выразим из соотношения (2) синус этого угла:
sinφmax=kmaxλ/d.
Отсюда
φmax=arcsin(kmaxλ/d).
Подставив сюда значения величин λ, d, kmах и произведя вычисления, получим
φmах=65,4°.
Задачи
Зоны Френеля
31.1. Зная формулу радиуса k-й. зоны Френеля для сферической волны (ρk=![]() ), вывести соответствующую формулу для плоской волны.
), вывести соответствующую формулу для плоской волны.
31.2. Вычислить радиус ρ5 пятой зоны Френеля для плоского волнового фронта (λ=0,5 мкм), если построение делается для точки наблюдения, находящейся на расстоянии b=1 м от фронта волны.
31.3. Радиус ρ4 четвертой зоны Френеля для плоского волнового фронта равен 3 мм. Определить радиус ρ6 шестой зоны Френеля.
31.4. На диафрагму с круглым отверстием диаметром d=4 мм падает нормально параллельный пучок лучей монохроматического света (λ=0,5 мкм). Точка наблюдения находится на оси отверстия на расстоянии b=1 м от него. Сколько зон Френеля укладывается в отверстии? Темное или светлое пятно получится в центре дифракционной картины, если в месте наблюдений поместить экран?
31.5. Плоская световая волна (λ=0,5 мкм) падает нормально на диафрагму с круглым отверстием диаметром d=l см. На каком расстоянии b от отверстия должна находиться точка наблюдения, чтобы отверстие открывало: 1) одну зону Френеля? 2) две зоны Френеля?
31.6. Плоская световая волна падает нормально на диафрагму с круглым отверстием. В результате дифракции в некоторых точках оси отверстия, находящихся на расстояниях bi, от его центра, наблюдаются максимумы интенсивности. 1. Получить вид функции b=f(r, λ, п), где r — радиус отверстия; λ — длина волны; п — число зон Френеля, открываемых для данной точки оси отверстием. 2. Сделать то же самое для точек оси отверстия, в которых наблюдаются минимумы интенсивности.
|
31.7. Плоская световая волна (λ=0,7 мкм) падает нормально на диафрагму с круглым отверстием радиусом r=1,4 мм. Определить расстояния b1, b2, b3 от диафрагмы до трех наиболее удаленных от нее точек, в которых наблюдаются минимумы интенсивности.
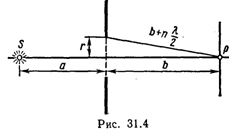
31.8. Точечный источник S света (λ=0,5 мкм), плоская диафрагма с круглым отверстием радиусом r=1 мм и экран расположены, как это указано на рис. 31.4 (а=1 м). Определить расстояние b от экрана до диафрагмы, при котором отверстие открывало бы для точки Р три зоны Френеля.
31.9. Как изменится интенсивность в точке Р (см. задачу 31.8), если убрать диафрагму?
Дифракция на щели. Дифракционная решетка
31.10. На щель шириной а=0,05 мм падает нормально монохроматический свет (λ=0,6 мкм). Определить угол φ между первоначальным направлением пучка света и направлением на четвертую темную дифракционную полосу.
31.11. На узкую щель падает нормально монохроматический свет. Угол φ отклонения пучков света, соответствующих второй светлой дифракционной полосе, равен 1°. Скольким длинам волн падающего света равна ширина щели?
31.12. На щель шириной а=0,1 мм падает нормально монохроматический свет (λ=0,5 мкм). За щелью помещена собирающая линза, в фокальной плоскости которой находится экран. Что будет наблюдаться на экране, если угол φ дифракции равен: 1) 17'; 2) 43'.
31.13. Сколько штрихов на каждый миллиметр содержит дифракционная решетка, если при наблюдении в монохроматическом свете (λ=0,6 мкм) максимум пятого порядка отклонен на угол φ=18°?
31.14. На дифракционную решетку, содержащую n=100 штрихов на 1 мм, падает нормально монохроматический свет. Зрительная труба спектрометра наведена на максимум третьего порядка. Чтобы навести трубу на другой максимум того же порядка, ее нужно повернуть на угол Δφ=20°. Определить длину волны λ света.

|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 |