31.15. Дифракционная решетка освещена нормально падающим монохроматическим светом. В дифракционной картине максимум второго порядка отклонен на угол φ1=14°. На какой угол φ2 откло­нен максимум третьего порядка?

31.16. Дифракционная решетка содержит n=200 штрихов на 1 мм. На решетку падает нормально монохроматический свет (λ=0,6 мкм). Максимум какого наибольшего порядка дает эта решетка?

31.17. На дифракционную решетку, содержащую n=400 штри­хов на 1 мм, падает нормально монохроматический свет (λ=0,6 мкм). Найти общее число дифракционных максимумов, которые дает эта решетка. Определить угол φ дифракции, соответствующий послед­нему максимуму.

31.18. При освещении дифракционной решетки белым светом спектры второго и третьего порядков отчасти перекрывают друг друга. На какую длину волны в спектре второго порядка наклады­вается фиолетовая граница (λ=0,4 мкм) спектра третьего порядка?

31.19. На дифракционную решетку, содержащую n=500 штри­хов на 1 мм, падает в направлении нормали к ее поверхности белый свет. Спектр проецируется помещенной вблизи решетки линзой на экран. Определить ширину b спектра первого порядка на экране, если расстояние L линзы до экрана равно 3 м. Границы видимости спектра λкр=780 им, λФ=400 нм.

31.20. На дифракционную решетку с периодом d=10 мкм под углом α=30° падает монохроматический свет с длиной волны λ=600 нм. Определить угол φ дифракции, соответствующий вто­рому главному максимуму.

31.21. Дифракционная картина получена с помощью дифрак­ционной решетки длиной l=1,5 см и периодом d=5 мкм. Определить, в спектре какого наименьшего порядка этой картины получатся раздельные изображения двух спектральных линий с разностью длин волн Δλ=0,1 нм, если линии лежат в крайней красной части спектра (λ760 нм).

31.22. Какой наименьшей разрешающей силой R должна обла­дать дифракционная решетка, чтобы с ее помощью можно было раз­решить две спектральные линии калия (λ1=578 нм и λ2=580 нм)? Какое наименьшее число N штрихов должна иметь эта решетка, чтобы разрешение было возможно в спектре второго порядка?

31.23. С помощью дифракционной решетки с периодом d=20 мкм требуется разрешить дублет натрия (λ1=589,0 нм и λ2=589,6 нм) в спектре второго порядка. При какой наименьшей длине l решетки это возможно?

31.24. Угловая дисперсия Dφ дифракционной решетки для излу­чения некоторой длины волны (при малых углах дифракции) сос­тавляет 5 мин/нм. Определить разрешающую силу R этой решетки для излучения той же длины волны, если длина l решетки равна 2 см.

31.25. Определить угловую дисперсию Dφ дифракционной решет­ки для угла дифракции φ==30° и длины волны λ=600 нм. Ответ вы­разить в единицах СИ и в минутах на нанометр.

31.26. На дифракционную решетку, содержащую n=500 штри­хов на 1 мм, падает нормально монохроматический свет с длиной волны λ=700 нм. За решеткой помещена собирающая линза с глав­ным фокусным расстоянием f=50 см. В фокальной плоскости линзы расположен экран. Определить линейную дисперсию Dl такой сис­темы для максимума третьего порядка. Ответ выразить в милли­метрах на нанометр.

31.27. Нормально поверхности дифракционной решетки падает пучок света. За решеткой помещена собирающая линза с оптичес­кой силой Ф=1 дптр. В фокальной плоскости линзы расположен экран. Определить число п штрихов на 1 мм этой решетки, если при малых углах дифракции линейная дисперсия Dl=1 мм/нм.

31.28. На дифракционную решетку нормально ее поверхности падает монохроматический свет (λ=650 нм). За решеткой находится линза, в фокальной плоскости которой расположен экран. На экра­не наблюдается дифракционная картина под углом дифракции φ=30°. При каком главном фокусном расстоянии f линзы линейная дисперсия Dl=0,5 мм/нм?

Дифракция на кристаллической решетке

31.29. На грань кристалла каменной соли падает параллельный пучок рентгеновского излучения (λ=147 пм). Определить расстоя­ние d между атомными плоскостями кристалла, если дифракционный максимум второго порядка наблюдается, когда излучение падает под углом =31°30' к поверхности кристалла.

31.30. Какова длина волны λ монохроматического рентгеновского излучения, падающего на кристалл кальцита, если дифракционный максимум первого порядка наблюдается, когда угол между на­правлением падающего излучения и гранью кристалла равен 3°?

Расстояние d между атомными плоскостями кристалла принять рав­ным 0,3 нм.

31.31. Параллельный пучок рентгеновского излучения падает на грань кристалла. Под углом =65° к плоскости грани наблю­дается максимум первого порядка. Расстояние d между атомными плоскостями кристалла 280 пм. Определить длину волны λ рентге­новского излучения.

Разрешающая сила объектива телескопа

31.32. Диаметр D объектива телескопа равен 8 см. Каково на­именьшее угловое расстояние β между двумя звездами, дифракцион­ные изображения которых в фокальной плоскости объектива по­лучаются раздельными? При малой освещенности глаз человека наиболее чувствителен к свету с длиной волны λ=0,5 мкм.

31.33. На шпиле высотного здания укреплены одна под другой две красные лампы (λ=640 нм). Расстояние d между лампами 20 см. Здание рассматривают ночью в телескоп с расстояния r=15 км. Определить наименьший диаметр Dmin объектива, при котором в. его фокальной плоскости получатся раздельные дифракционные изображения.

§ 32. ПОЛЯРИЗАЦИЯ СВЕТА

Основные формулы

• Закон Брюстера

tg εB =n21,

где εB — угол падения, при котором отраженная световая волна полностью поляризована; n21 — относительный показатель прелом­ления.

• Закон Малюса

I=I0cos2α,

где I — интенсивность плоскополяризованного света, прошедшего через анализатор; I0 — интенсивность плоскополяризованного све­та, падающего на анализатор; α — угол между направлением колеба­ний светового вектора волны, падающей на анализатор, и плоско­стью пропускания анализатора.

• Степень поляризации света

,

где Imax и Imin — максимальная и минимальная интенсивности частично поляризованного света, пропускаемого анализатором.

• Угол поворота φ плоскости поляризации оптически актив­ными веществами определяется соотношениями:

а) в твердых телах φ=αd, где α — постоянная вращения; d — длина пути, пройденного светом в оптически активном веществе;

б) в чистых жидкостях φ=[α]ρd, где [α] — удельное вращение; ρ — плотность жидкости;

в) в растворах φ=[α]Cd, где С — массовая концентрация опти­чески активного вещества в растворе.

Примеры решения задач

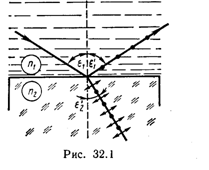
Пример 1. Пучок естественного света падает на полированную поверхность стеклянной пластины, погруженной в жидкость. Отраженный от пластины пучок света составляет угол φ=97° с падаю­щим пучком (рис. 32.1). Определить показатель преломления n жидкости, если отраженный свет полностью по­ляризован.

Решение. Согласно закону Брюстера, свет, отраженный от ди­электрика, полностью поляризован в том случае, если тангенс угла паде­ния

tg ε1B=n21,

где n21 — относительный показатель преломления второй среды (стекла) относительно первой (жидкости).

Относительный показатель преломления равен отношению аб­солютных показателей преломления этих сред. Следовательно,

tg ε1B=n2/n1.

Согласно условию задачи, отраженный луч повернут на угол φ от­носительно падающего луча. Так как угол падения равен углу отра­жения, то ε1B=φ/2 и, следовательно, tg(φ/2)=n2/n1, откуда

.

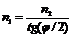Сделав подстановку числовых значений, получим n1=l,33.

Пример 2. Два николя N1 и N2 расположены так, что угол a между их плоскостями пропускания равен 60°. Определить: 1) во сколько раз уменьшится интенсивность света при прохождении че­рез один николь (N1); 2) во сколько раз уменьшится интенсивность света при прохождении через оба николя? При прохождении каждо­го из николей потери на отражение и поглощение света составляют 5 %.

Решение 1. Пучок естественного света, падая на грань ни­коля N1 (рис. 32.2), расщепляется вследствие двойного лучепрелом­ления на два пучка: обыкновенный и необыкновенный. Оба пучка одинаковы по интенсивности и полностью поляризованы. Плоскость колебаний для необыкновенного пучка лежит в плоскости чертежа (плоскость главного сечения). Плоскость колебаний для обыкновенного пучка перпендикулярна плоскости чертежа. Обыкновенный пучок (o) вследствие полного отражения от границы АВ отбрасы­вается на зачерненную поверхность призмы и поглощается ею. Необыкновенный пучок (е) проходит через николь. При этом интен­сивность света уменьшается вследствие поглощения в веществе николя.

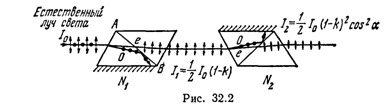
Таким образом, интенсивность света, прошедшего через николь N1,

I1=1/2I0(1-k),

где k=0,05— относительная потеря интенсивности света в николе; I0 — интенсивность естественного света, падающего на николь N1.

Относительное уменьшение интенсивности света получим, разде­лив интенсивность I0 естественного света на интенсивность I1 по­ляризованного света:

.

Подставив числовые значения, найдем

I0/I1=2,10.

Таким образом, интенсивность света при прохождении через николь N1 уменьшается в 2,10 раза.

2. Пучок плоскополяризованного света интенсивности I1 падает на николь N2 и также расщепляется на обыкновенный и необыкновен­ный. Обыкновенный пучок полностью поглощается в николе, а ин­тенсивность необыкновенного пучка света, вышедшего из николя, определяется законом Малюса (без учета поглощения в этом николе):

I2=I1cos2α

где α — угол между плоскостью колебаний в поляризованном пучке и плоскостью пропускания николя N2.

Учитывая потери интенсивности во втором николе, получим

I2=I1 (l—k) cos2 α.

Искомое уменьшение интенсивности при прохождении света че­рез оба николя найдем, разделив интенсивность I0 естественного света на интенсивность I2 света, прошедшего систему из двух николей:

.

Подставив данные, произведем вычисления:

Пример 3. Пучок частично-поляризованного света рассматри­вается через николь. Первоначально николь установлен так, что его плоскость пропускания параллельна плоскости колебаний линейно-поляризованного света. При повороте николя на угол (φ=60° интен­сивность пропускаемого им света уменьшилась в k=2 раза. Опреде­лить отношение Ie/Iп интенсивностей естественного и линейно-поля­ризованного света, составляющих данный частично-поляризован­ный свет, а также степень поляризации Р пучка света.

В соответствии с условием задачи I1=k*I2, или

Ie/Iп = 1, или Ie = Iп ,

т. е. интенсивности естественного и поляризованного света в задан­ном пучке равны между собой.

Степень поляризации частично-поляризованного света определя­ется соотношением

P = (Imax – Imin)/(Imax + Imin), (1)

где Imax и Imin — соответственно максимальная и минимальная ин­тенсивности света, пропущенного через николь.

Максимальная интенсивность Imax = I1 = Iп + ½ Ie, или, учи­тывая, что Ie = Iп

Imax = 3/2 Iп

Минимальная интенсивность соответствует положению николя, при котором плоскость пропускания его перпендикулярна плоско­сти колебаний линейно-поляризованного света. При таком положе­нии николя поляризованный свет будет полностью погашен и через николь пройдет только половина интенсивности естественного света. Общая интенсивность выразится равенством

Imin = ½ Ie= ½ Iп

Следовательно, степень поляризации пучка света

P = ½ .

Пример 4. Пластинка кварца толщиной d1=1 мм, вырезанная перпендикулярно оптической оси кристалла, поворачивает пло­скость поляризации монохроматического света определенной длины волны на угол φ1=20°. Определить: 1) какова должна быть толщина d2 кварцевой пластинки, помещенной между двумя «параллельными» николями, чтобы свет был полностью погашен; 2) какой длины l труб­ку с раствором сахара массовой концентрацией С=0,4 кг/л надо поместить между николями для получения того же эффекта? Удель­ное вращение [α] раствора сахара равно 0,665 град/(м*кг*м-3).

Решение. 1. Угол поворота плоскости поляризации кварце­вой пластинкой определяется соотношением φ = α *d.

Пользуясь этой формулой, выразим искомую толщину d2 пла­стинки:

d2 = φ2 / α (1)

где φ2 — угол поворота плоскости поляризации, при котором свет будет полностью погашен (φ2 =90°).

Постоянную вращения α для кварца найдем также из формулы φ=α*d, подставив в нее заданные в условии задачи значения d1 и φ1:

α = φ1 / d1

Подставив это выражение α в формулу (1), получим

d2 = (φ2/ φ1) d1

Произведя вычисления по этой формуле, найдем толщину пла­стинки:

d2 = 4,5 мм.

2. Длину трубки с сахарным раствором найдем из соотношения φ2=[α]Cd, выражающего угол поворота плоскости поляризации раствором сахара, где d — толщина раствора сахара (принимается равной длине l трубки). Отсюда получим

l = φ2/([α]C).

Подставив сюда значения φ2, [α], C=0,4 кг/л ==400 кг/м3 и произведя вычисления, найдем

l =3,8 дм.

Задачи

Закон Брюстера. Закон Малюса

32.1. Пучок света, идущий в воздухе, падает на поверхность жидкости под углом ε1=54°. Определить угол преломления ε`2 пуч­ка, если отраженный пучок полностью поляризован.

32.2. На какой угловой высоте φ над горизонтом должно нахо­диться Солнце, чтобы солнечный свет, отраженный от поверхности воды, был полностью поляризован?

32.3. Пучок естественного света, идущий в воде, отражается от грани алмаза, погруженного в воду. При каком угле падения εв =отраженный свет полностью поляризован?

32.4. Угол Брюстера εв при падении света из воздуха на кристалл каменной соли равен 57°. Определить скорость света в этом кристал­ле.

32.5. Предельный угол ε`1 полного отражения пучка света на гра­нице жидкости с воздухом равен 43°. Определить угол Брюстера εв для падения луча из воздуха на поверхность этой жидкости.

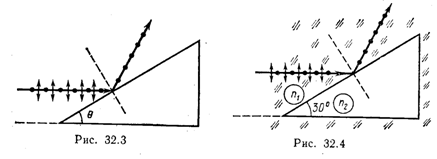
32.6. Пучок естественного света падает на стеклянную (n=1,6) призму (рис. 32.3). Определить двугранный угол θ призмы, если отраженный пучок максимально поляризован.

32.7. Алмазная призма находится в некоторой среде с показа­телем преломления n1. Пучок естественного света падает на призму так, как это показано на рис. 32.4. Определить показатель прелом­ления n1 среды, если отраженный пучок максимально поляризован.

32.8. Параллельный пучок естественного света падает на сфери­ческую каплю воды. Найти угол α между отраженным и падающим пучками в точке А (рис. 32.5).

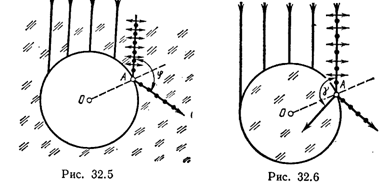32.9. Пучок естественного света падает на стеклянный шар (п= 1,54). Найти угол γ между преломленным и падающим пучками в точке А (рис. 32.6).

32.10. Пучок естественного света падает на стеклянный шар, находящийся в воде. Найти угол φ между отраженным и падающим пучками в точке А (рис. 32.7). Показатель преломления n стекла принять равным 1,58.

32.11. Анализатор в k=2 раза уменьшает интенсивность света, приходящего к нему от поляризатора. Определить угол α между плоскостями пропускания поляризатора и анализатора. Потерями интенсивности света в анализаторе пренебречь.

32.12. Угол α между плоскостями пропускания поляризатора и анализатора равен 45°. Во сколько раз уменьшится интенсивность света, выходящего из анализатора, если угол увеличить до 60°?

32.13. Во сколько раз ослабляется интенсивность света, прохо­дящего через два николя, плоскости пропускания которых образуют угол α=30°, если в каждом из николей в отдельности теряется 10 % интенсив­ности падающего на него света?

32.14. В фотометре одновременно рассматривают две половины поля зрения: в одной видна эталонная све­тящаяся поверхность с яркостью L1=5 ккд/м2, в другой — испытуемая поверхность, свет от которой прохо­дит через два николя. Граница меж­ду обеими половинами поля зрения исчезает, если второй николь повер­нуть относительно первого на угол

α=45°. Найти яркость L2 испытуемой поверхности, если извест­но, что в каждом из николей интенсивность падающего на него све­та уменьшается на 8 %.

Степень поляризации света

32.15. В частично-поляризованном свете амплитуда светового вектора, соответствующая максимальной интенсивности света, в n=2 раза больше амплитуды, соответствующей минимальной ин­тенсивности. Определить степень поляризации Р света.

32.16. Степень поляризации Р частично-поляризованного света

равна 0,5. Во сколько раз отличается максимальная интенсивность света, пропускаемого через анализатор, от минимальной?

32.17. На пути частично-поляризованного света, степень поля­ризации Р которого равна 0,6, поставили анализатор так, что интен­сивность света, прошедшего через него, стала максимальной. Во сколько раз уменьшится интенсивность света, если плоскость пропускания анализатора повернуть на угол α =30°?

32.18. На николь падает пучок частично-поляризованного света. При некотором положении николя интенсивность света, прошедшего через него, стала минимальной. Когда плоскость пропускания нико­ля повернули на угол β =45°, интенсивность света возросла в k = 1,5 раза. Определить степень поляризации Р света.

Вращение плоскости поляризации

32.19. Пластинку кварца толщиной d1=2 мм, вырезанную перпен­дикулярно оптической оси, поместили между параллельными николями, в результате чего плоскость поляризации света повернулась на угол φ =53°. Определить толщину d2 пластинки, при которой данный монохроматический свет не проходит через анализатор.

32.20. Никотин (чистая жидкость), содержащийся в стеклянной трубке длиной d=8 см, поворачивает плоскость поляризации жел­того света натрия на угол φ =137°. Плотность никотина ρ=1,01*103 кг/м3. Определить удельное вращение [α] никотина.

32.21. Раствор глюкозы с массовой концентрацией Ci=280 кг/м3, содержащийся в стеклянной трубке, поворачивает плоскость поляри­зации монохроматического света, проходящего через этот раствор, на угол φ =32°. Определить массовую концентрацию С2 глюкозы в другом растворе, налитом в трубку такой же длины, если он пово­рачивает плоскость поляризации на угол φ =24°.

32.22. Угол φ поворота плоскости поляризации желтого света натрия при прохождении через трубку с раствором сахара равен 40°. Длина трубки d=15 см. Удельное вращение [α] сахара равно 1.17*10-2 рад*м3/(м*кг). Определить плотность ρ раствора.

§ 33. ОПТИКА ДВИЖУЩИХСЯ ТЕЛ

Основные формулы

• Эффект Доплера в релятивистском случае

а) источник удаляется от наблюдателя ( J =0)

б) источник приближается к наблюдателю ( J = π)

• Эффект Доплера в нерелятивистском случае

где ∆v — изменение частоты (∆v = v-v0 ).

• Эффект Вавилова — Черенкова. При движении заряжен­ной частицы в некоторой среде со скоростью v, больше фазовой скорости света в данной среде, возникает излучение света. Свет этот распространяется по направлениям, составляющим острый угол с траекторией частицы, т. е. вдоль образующих конуса, ось кото­рого совпадает с направлением скорости частицы. Угол J определя­ется из соотношения

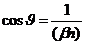
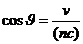
или

где n — показатель преломления среды, в котором движется заря­женная частица.

Примеры решения задач

Пример 1. Источник монохроматического света с длиной волны λ0=600 нм движется по направлению к наблюдателю со скоростью v=0,1с (с—скорость распространения электромагнитных волн). Определить длину волны λ излучения, которую зарегистрирует спектральный прибор наблюдателя.

Решение. В системе отсчета, связанной с наблюдателем, спектральный прибор зарегистрирует электромагнитное излучение частоты

(1)

где vo — собственная частота монохроматического излучения источ­ника; β=v/c; J — угол между вектором v и направлением наблюде­ния, измеренный в системе отсчета, связанной с наблюдателем.

Выразим частоты v и v0 через длины волн λ и λ0: v=c/λ и v0=c/λ0 Заметив, что в нашем случае = π(cos = -1), перепишем формулу (1) с учетом последних соотношений:

откуда

Подставим значения β(β =v/c=0,1) и λ0 в полученное выражение и произведем вычисления:

λ = 542 нм.

Пример 2. Каким минимальным импульсом pmin (в единицах МэВ/с)

должен обладать электрон, чтобы эффект Вавилова — Черенкова можно было наблюдать в воде?

Решение. Эффект Вавилова — Черенкова состоит в излуче­нии света, возникающем при движении в веществе заряженных частиц со скоростью v, превышающей скорость распространения световых волн (фазовую скорость) в этой среде. Так как фазовая скорость света vф=c/n (с — скорость распространения электромаг­нитного излучения в вакууме; п — показатель преломления среды), то условием возникновения эффекта Вавилова — Черенкова явля­ется

v>vф, или v>c/n.

Обычно это условие записывают иначе, учитывая, что β=v/c:

βn>1. (1)

Поскольку черенковское излучение наблюдается для релятивист­ских частиц, то запишем сначала выражение для релятивистского импульса:

P=mv=m0v/(1-β2 )0.5, или p=m0cβ/(1-β2)0.5

где учтено, что v=βc.

Минимальному импульсу соответствует минимальное значение βmin которое находим из условия (1):

βmin=1/n.

Тогда минимальное значение импульса

Pmin=m0c/(n2-1)0.5 (2)

Вычисления выполним во внесистемных единицах — МэВ/с (с — скорость распространения электромагнитного излучения). Для этого поступим следующим образом. Известно, что m0c2=0,511МэВ, от­сюда запишем m0c =0,511 МэВ/с.

Подставив в (2) n=l,33 и най­денное значение m0c, произведем вычисления:

pmin=0,583 МэВ/с.

Задачи

Эффект Доплера

33.1. При какой предельной скорости v (в долях скорости света) источника можно вместо релятивистской формулы для эффекта Доплера пользоваться прибли­женным выражением υ»υ0(l-β), если погрешность в определении частоты не должна превышать 1 %?

33.2. Для определения угловой скорости вращения солнечного диска измеряли относительный сдвиг ∆λ/λ спектральных линий от восточного и западного краев Солнца. Он оказался равным 1,5*10-5. Определить угловую скорость w вращения солнечного диска. Радиус R Солнца считать известным.

33.3. Космический корабль удаляется от Земли со скоростью v=10 км/с. Частота υ0 электромагнитных волн, излучаемых антенной корабля, равна 30 МГц. Определить доплеровское смещение ∆υ частоты, воспринимаемой приемником.

33.4. При изучении спектра излучения некоторой туманности линия излучения водорода (λα = 656,3 нм) оказалась смещенной на ∆λ=2,5 нм в область с большей длиной волны (красное смещение). Найти скорость v движения туманности относительно Земли и ука­зать, удаляется она от Земли или приближается к ней.

33.5. Определить обусловленное эффектом Доплера уширение ∆λ/λ спектральных линий излучения атомарного водорода, находя­щегося при температуре Т =300 К.

33.6. В результате эффекта Доплера происходит уширение ли­ний γ-излучения ядер. Оценить уширение ∆λ/λ линий γ-излучения ядер кобальта, находящихся при температуре; 1) комнатной (T=290 К); 2) ядерного взрыва (T=10 МК).

33.7. Два космических корабля движутся вдоль одной прямой. Скорости v1 и v2 их в некоторой инерциальной системе отсчета соот­ветственно 12 и 8 км/с. Определить частоту υ сигнала электромаг­нитных волн, воспринимаемых вторым космическим кораблем, если антенна первого корабля излучает электромагнитные волны ча­стотой υ0=l МГц. Рассмотреть следующие случаи: 1) космические корабли движутся навстречу друг другу; 2) космические корабли удаляются друг от друга в противоположных направлениях; 3) пер­вый космический корабль нагоняет второй; 4) первый космический корабль удаляется от второго, движущегося в том же направлении.

33.8. Монохроматический свет с длиной волны λ=600 нм падает на быстро вращающиеся в противоположных направлениях зеркала (опыт ). После N=10 отражений от зеркал пу­чок света попадает в спектрограф. Определить изменение ∆λ длины волны света, падающего на зеркала нормально их поверхности. Ли­нейная скорость v зеркал равна 0,67 км/с. Рассмотреть два случая, когда свет отражается от зеркал: 1) движущихся навстречу одно дру­гому; 2) удаляющихся одно от другого.

33.9. Плоское зеркало удаляется от наблюдателя со скоростью v вдоль нормали к плоскости зеркала. На зеркало посылается пучок света длиной волны λ0 нм. Определить длину волны λ света, отраженного от зеркала, движущегося со скоростью: 1) 0,2с (с — скорость в вакууме); 2) 9 км/с.

33.10. Приемник радиолокатора регистрирует частоты биений между частотой сигнала, посылаемого передатчиком, и частотой сиг­нала, отраженного от движущегося объекта. Определить скорость v приближающейся по направлению к локатору ракеты, если он рабо­тает на частоту v0=600 МГц и частота v1 биений равна 4 кГц.

33.11. Рассказывают, что известный физик Роберт Вуд, проехав однажды на автомашине на красный свет светофора, был остановлен блюстителем порядка. Роберт Вуд, сославшись на эффект. Доплера, уверял, что он ехал достаточно быстро и красный свет светофора для него изменился на зеленый. Оценить скорость v, с которой должна была бы двигаться автомашина, чтобы красный сигнал светофора (λ1=650 нм) воспринимался как зеленый (λ2=550 нм).

33.12. Длины волн излучения релятивистских атомов, движу­щихся по направлению к наблюдателю, оказались в два раза меньше, чем соответствующие длины волн нерелятивистских атомов. Опре­делить скорость v (в долях ско­рости света) релятивистских атомов.

33.13. Наиболее короткая длина волны λ1 в спектре излу­чения водорода равна 410 нм.

С какой скоростью v должно уда­ляться от нас скопление атомов водорода, чтобы их излучение оказалось вследствие эффекта Доплера за пределами видимой части спектра. Граница видимой части спектра соответствует дли­не волны λ2=760 нм.

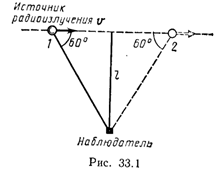
33.14. На некотором расстоянии l от наблюдателя (рис. 33.1) прямолинейно со скоростью v=0,6 с движется источник радиоизлу­чения, собственная частота υ0 которого равна 4 ГГц. В каких пре­делах изменяется частота υ сигнала, воспринимаемого наблюдате­лем, если наблюдение ведется в течение всего времени движения ис­точника из положения 1 в положение 2? Углы указаны в системе отсчета, связанной с наблюдателем.

Эффект Вавилова—Черенкова

33.15. Какой наименьшей скоростью v должен обладать электрон, чтобы в среде с показателем преломления п= 1,60 возникло черенковское излучение?

33.16. При какой скорости v электронов (в долях скорости света) черенковское излучение происходит в среде с показателем преломле­ния n=1,80 под углом =20° к направлению их движения?

33.17. Найти наименьшую ускоряющую разность потенциалов Umin
которую должен пройти электрон, чтобы в среде с показа­телем преломления n=1,50 возникло черенковское излучение.

33.18. Известно, что быстрые частицы, входящие в состав кос­мического излучения, могут вызывать эффект Вавилова — Черенко­ва в воздухе (п= 1,00029). Считая, что такими частицами являются электроны, определить их минимальную кинетическую энергию.

33.19. Электрон с кинетической энергией T=0,51 МэВ движется в воде. Определить угол J, составляемый черенковским излучением с направлением движения электрона.

33.20. Импульс релятивистского электрона равен m0c. При каком минимальном показателе преломления nmin среды уже можно наб­людать эффект Вавилова — Черенкова?

33.21. Мю - и пи-мезоны имеют одинаковые импульсы р= 100 МэВ/с. В каких пределах должен быть заключен показатель преломления п среды, чтобы для m - мезонов черенковское излучение наблюдалось, а для π - мезонов — нет.

* Считать, что среды по обе стороны линзы одинаковы.

* Мениском называют линзу, ограниченную двумя сферическими поверх­ностями, имеющими одинаковое направление кривизны.

* Источник называется изотропным, если сила света источника одина­кова во всех направлениях.

* При решении задач по фотометрии электрические лампочки принимать за изотропные точечные источники света.

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3