Матричная оптика – оптические матрицы

В матричной оптике любая осесимметричная система описывается 2×2 матрицей

,

которая называется оптической матрицей системы. Пусть световой луч на входе в систему задается своей высотой и углом наклона (все это относительно оси системы), т. е характеризуется двумерным вектором

.

Тогда после прохождения через систему высота и угол наклона будут

,

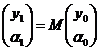т. е.

.

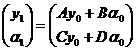Оптическая матрица системы является последовательным произведением элементарных оптических матриц – матриц перемещения, преломления, отражения.

Матрица перемещения. Для получения матрицы перемещения рассмотрим световой луч, входящий в систему на высоте с углом наклона и свободно распространяющийся вправо на расстояние .


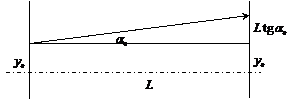Рис. 1. Высота светового луча на входе , на выходе

, угол не меняется

Тогда на выходе из системы его высота будет . Учитывая условие параксиальности, в частности малость угла , можно заменить тангенс этого угла на сам угол и получить

.

Учитывая, что луч распространяется в свободном пространстве, имеем также

.

Последние два соотношения можно записать в матричном виде

.

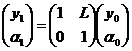Итак, перемещение светового луча в свободном пространстве на расстояние описывается матрицей

которая и называется матрицей перемещения.

Матрица отражения. Переходим к отражению. Пусть световой луч отражается от сферического зеркала радиуса . При этом отражение происходит на высоте и до отражения луч имеет угол наклона . Мы используем два подхода для вывода матрицы отражения. Первый из них геометрический, как для матрицы перемещения, второй использует парксиальную или гауссову оптику.

Первый – геометрический вывод. Очевидно, что непосредственно при отражении высота луча не изменится, т. е.

,

а вот угол наклона поменяется, и каким образом, мы сейчас подсчитаем.


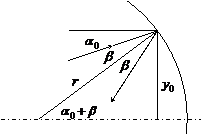Рис. 2. При отражении высота светового луча не меняется,

угол падения и угол отражения равны

Так как зеркало сферическое, нормаль к нему совпадает с радиусом. Угол между световым лучом и радиусом – угол падения, обозначим , угол отражения тоже будет . Поэтому угол наклона отраженного луча будет 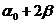, а с учетом того, что после отражения луч будет двигаться в противоположном направлении и мы должны будем изменить положительное направление оси , на самом деле будет

.

Прямоугольный треугольник на рисунке 2 дает нам 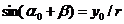или, учитывая малость углов, просто , поэтому

.

Окончательно,

.

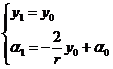Записав это в матричном виде, получаем

.

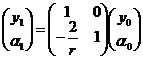Итак, отражение светового луча от зеркала радиуса описывается матрицей

,

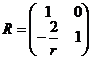которая называется матрицей отражения.

Добавим, что для луча, движущегося в обратном направлении, матрицы перемещения и отражения имеют тот же самый вид.

Второй вывод – используем гауссову оптику. Воспользуемся тем фактом, что в области параксиальной оптики луч, идущий параллельно оси зеркала, т. е. луч

,


после отражения попадает в фокус сферического зеркала, расположенный на расстоянии от его вершины

Рис. 3 Параксиальный луч, идущий параллельно оси зеркала, после отражения

попадает в фокус, расположенный на расстоянии от вершины

Конечно же, непосредственно после отражения высота луча тоже будет равна , а как показывает рисунок, угол наклона луча будет 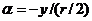, т. е. отраженный луч, характеризуется вектором

.

И это означает, что

.

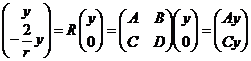Из равенства первых координат левого и правого векторов следует, что , из равенства вторых координат следует, что .

Теперь обратим направление только что рассмотренного луча. Тогда луч до отражения будет задаваться вектором

,

а после отражения

.

И это означает, что

.

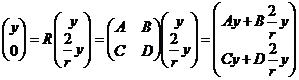Опять приравняем первые координаты, тогда из того, что , следует, что . А из равенства вторых координат следует, что 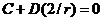. Вместе с 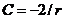это дает, что . Итак, все элементы матрицы отражения найдены, и мы опять имеем

.

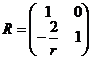Матрица тонкой линзы. Теперь, как только что мы сделали, с помощью гауссовой оптики найдем матрицу преломления для тонкой линзы с фокусным расстоянием . Запустим два световых луча.


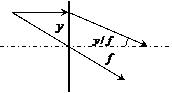Рис. 4 Первый луч идет параллельно оси и после прохождения через линзу попадает в

фокус, второй луч входит в линзу на нулевой высоте и не меняет своего направления

Первый из них идет параллельно оси на высоте , т. е. характеризуется вектором

.

После прохождения через линзу он попадает в фокус, т. е. непосредственно на линзе он задается вектором

.

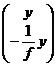Т. к. эти два вектора связаны соотношением (матрицу тонкой линзы, как и матрицу отражения, обозначают той же буквой )

,

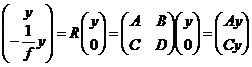отсюда сразу получаем , .

Второму лучу и до и после отражения соответствует вектор

.

И это означает, что

,

а отсюда следует и . Итак, матрица тонкой линзы имеет вид

.

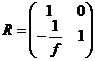И матрицу отражения, и матрицу преломления можно записать в виде

,

где – оптическая сила соответствующего устройства.

Здесь изложена всего лишь сокращенная версия оснований матричной оптики.

Подробное изложение имеется в книге: Бёрч Дж. М. Введение в матричную оптику, 1978. Есть в электронной библиотеке мехмата МГУ, расположенной по адресу

http://lib. *****/

Второй источник – конспект лекций: Основы оптики.– СПб: СПб ГИТМО (ТУ), 2000, расположен по адресу

http://aco. *****/el_books/basics_optics/index. html

А вообще, http://aco. *****/ – это сайт кафедры прикладной и компьютерной оптики Ленинградского института точной механики и оптики (ЛИТМО), который недавно стал называться Санкт-Петербургским государственным университетом информационных технологий, механики и оптики (ИТМО).