Практические работы
по математике
1. Нахождение предела функции. Первый и второй замечательные пределы.
2. Производная сложной функции. Исследование функции одной переменной и построение графиков.
3. Контрольная работа «Применение дифференциального исчисления к исследованию функций».
4. Нахождение неопределенных интегралов. Вычисление определенных интегралов.
5. Вычисление определителей.
6. Решение систем линейных уравнений методом Крамера. Контрольная работа.
7. Решение задач по теме «Множества». Формулы алгебры логики.
8. Вычисление вероятностей случайных событий. Формула полной вероятности.
9. Вычисление числовых характеристик.
10. Контрольная работа «Основы теории вероятностей и математической статистики»
11. Тригонометрическая форма комплексного числа.
12. Действия с комплексными числами в различных формах.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ПРОВЕДЕНИЮ ПРАКТИЧЕСКИХ РАБОТ ПО МАТЕМАТИКЕ
2 КУРС
Практическое занятие - это форма организации учебного процесса, предполагающая выполнение студентами по заданию и под руководством преподавателя одной или нескольких практических работ.
Дидактическая цель практических работ - формирование у студентов профессиональных умений, а также практических умений, необходимых для изучения последующих учебных дисциплин, а также подготовка к применению этих умений в профессиональной деятельности.
Так, на практических занятиях по математике у студентов формируется умение решать задачи, которое в дальнейшем должно быть использовано для решения профессиональных задач по специальным дисциплинам.
В ходе практических работ студенты овладевают умениями пользоваться информационными источниками, работать с нормативными документами и инструктивными материалами, справочниками, выполнять чертежи, схемы, таблицы, решать разного рода задачи, делать вычисления.
Задачи, которые решаются в ходе практических занятий по математике:
1) расширение и закрепление теоретических знаний по математике, полученных в ходе лекционных занятий;
2) формирование у студентов практических умений и навыков, необходимых для успешного решения задач по математике;
3) развитие у студентов потребности в самообразовании и совершенствовании знаний и умений в процессе изучения математики;
4) формирование творческого отношения и исследовательского подхода в процессе изучения математики;
5) формирование профессионально-значимых качеств будущего специалиста и навыков приложения полученных знаний в профессиональной сфере.
Практическое занятие №1. Вычисление пределов функций. Первый и второй замечательные пределы.
Тема: Вычисление пределов функций.
Цель: приобретение базовых знаний в области фундаментальных разделов математики. Проверка усвоения знаний по вычислению пределов функций. Повторить и систематизировать знания по данной теме.
Задачи:
• развитие творческого профессионального мышления;
• овладение языком науки, навыки оперирования понятиями;
• овладение умениями и навыками постановки и решения задач;
• углубление теоретической и практической подготовки;
• развитие инициативы и самостоятельности студентов.
•закрепление вычислительных навыков;
•продолжить работу над математической речью.
•формирование навыков самостоятельной работы, работы с учебником, навыки самостоятельного добывания знаний;
•развитие умения выделять главное при работе с текстом;
•формирование самостоятельности мышления, мыслительных операций: сравнение, анализ, синтез, обобщение, аналогия;
•показать обучающимся роль систематической работы по углублению и повышению прочности знаний, по культуре выполнения заданий;
•развитие творческих способностей учащихся.
Обеспечение практической работы:
Теоретический материал методической рекомендации к практической работе.
Математика. М:Форум-Инфа 2008.
, . Математика, – Серия: Среднее профессиональное образование. - Ростов-на-Дону «Феникс»,с.
Индивидуальные карточки с вариантом практической работы.
Ход практического занятия.
1.Формулирование темы занятия, пояснение связи темы с другими темами учебной дисциплины;
2.Проверка готовности обучающихся к занятию;
3.Проведение непосредственно занятия согласно тематике и в соответствии с рабочей программой дисциплины:
Изучить теоретический материал по теме «Вычисление пределов функций».
Рассмотреть примеры решения типовых заданий.
Выполнить самостоятельную работу по вычислению пределов функций с использованием первого и второго замечательного пределов.
Ответить на контрольные вопросы.
Теоретические сведения и методические рекомендации
по решению задач.
1. Изложение теоретического материала.
Чтобы вычислить предел функции в точке, надо:
1) Подставить вместо переменной x то, к чему x стремится.
2) Если после выполнения пункта 1) получим неопределенность вида ![]() , то надо числитель и знаменатель дроби разложить на множители и сократить дробь, или числитель и знаменатель домножить на сопряженное и после этого сократить дробь. Заметим, что дробь всегда будет сокращаться, если в выражении x
, то надо числитель и знаменатель дроби разложить на множители и сократить дробь, или числитель и знаменатель домножить на сопряженное и после этого сократить дробь. Заметим, что дробь всегда будет сокращаться, если в выражении x![]() а стрелку заменить на минус: (x-а).
а стрелку заменить на минус: (x-а).
3) Если после выполнения пункта 1) получим неопределенность вида ![]() , то надо числитель и знаменатель дроби разделить на старшую степень неизвестного, или слагаемое с самой большой степенью в числителе разделить на слагаемое с самой большой степенью в знаменателе и взять предел от результата деления.
, то надо числитель и знаменатель дроби разделить на старшую степень неизвестного, или слагаемое с самой большой степенью в числителе разделить на слагаемое с самой большой степенью в знаменателе и взять предел от результата деления.
4) Если после выполнения пункта 1) получим неопределенность вида ![]() , связанная с значениями тригонометрических функций, надо воспользоваться первым замечательным пределом.
, связанная с значениями тригонометрических функций, надо воспользоваться первым замечательным пределом.
Определение. Первым замечательным пределом называется предел
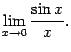
Первый замечательный предел равен
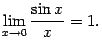
5) Определение: Вторым замечательным пределом называется предел
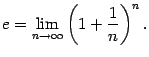
Число ![]() , заданное этим пределом, играет очень большую роль как в математическом анализе, так и в других разделах математики. Число
, заданное этим пределом, играет очень большую роль как в математическом анализе, так и в других разделах математики. Число ![]() называют основанием натуральных логарифмов (
называют основанием натуральных логарифмов (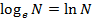 ).
).
Теорема. Второй замечательный предел существует. Его значение -- число, лежащее между и .
Более подробное изучение числа ![]() показывает, что
показывает, что ![]() -- иррациональное число, несколько первых десятичных знаков которого таковы:
-- иррациональное число, несколько первых десятичных знаков которого таковы:
![]()
2. Закрепление изученного материала.
Пример 1
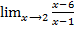 =
=![]() = -4
= -4
Мы воспользовались правилом 1) и подставили вместо x то, к чему x стремиться, т. е. x=2.
Пример 2
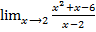 =
=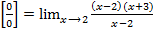 =
=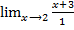 =
=![]() =5
=5
Пример 3
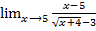 =
=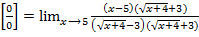 =
=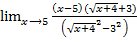 =
=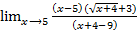 =
=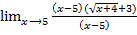 =
=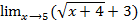 =3+3=6
=3+3=6
Пример 4
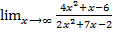 =
=![]() =
=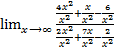 =
=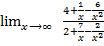 =
=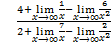 =
=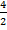
Пример 5
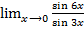 =
=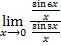 =
=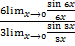 =
= =2
=2
Пример 6
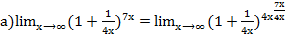 =
=![]()
б) 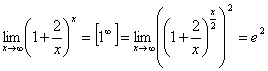
в) 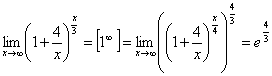
г) 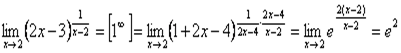
3. Закрепление знаний, умений и навыков.
Выполнить самостоятельную работу по вычислению пределов функций.
Практическая работа №1. Вариант 1 Вычислите предел функции: 1. 2. 3. 4. 5. 6. 7. 8. 9 10. | Практическая работа №1. Вариант 2 Вычислите предел функции: 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. |
Практическая работа № 2.
Тема: Нахождение производной функции. Исследование функции одной переменной и построение графика.
Цель: Проверить на практике знание понятия производной функции, умение находить производные элементарных функций, сложных функций, обратных функций, пользуясь таблицей производных и правилами дифференцирования, понятием сложная и обратная функция, умение применять производную для исследования функций.
Обеспечение практической работы:
Теоретический материал методической рекомендации к практической работе.
Учебник. «Математика». – М.: Дрофа, 2010.
Математика. М:Форум-Инфа 2008.
Индивидуальные карточки с вариантом практической работы.
1.Теоретический материал и примеры нахождения производной функции.
Определение: Производной функции f(x) (f'(x)) в точке x называется предел отношения приращения функции к приращению аргумента при приращении аргумента стремящемся к нулю:
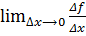 =f′(x)
=f′(x)
Производные элементарных функций.

Правила дифференцирования.
Если у функций f(x) и g(x) существуют производные, то
1.С′=0
2. (u+v)′=u′+v′
3. (uv)′=u′v+v′u
4. (С·u)′=С·u′, где С=соnst
5. (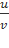 )′=
)′=![]()
6. Производная сложной функции:
f′(g(x))=f′(g)·g′(x)
2. Примеры.
1. Найти значение производной функции:y=3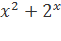 -4x+8.
-4x+8.
Решение:
По правилу нахождения производной алгебраической суммы функций (формула 2):
y′= (3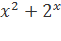 -4x+8)′= (3
-4x+8)′= (3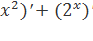 -(4x)′+(8)′=3·2x+
-(4x)′+(8)′=3·2x+![]() ·
·![]() -4·1+0=6x+
-4·1+0=6x+![]() ·
·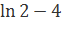
2. Найти значение производной функции: y =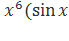 +4).
+4).
Решение:
Функция представляет собой произведение двух множителей: u=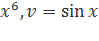 +4. По формуле 3:
+4. По формуле 3:
y′ =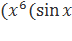 +4))′ =
+4))′ = 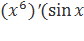 +4)+
+4)+ 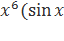 +4)′=6
+4)′=6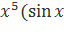 +4)+
+4)+![]() ·
·![]() .
.
3. Найти значение производной функции: y=![]() .
.
Решение:
Функция представляет собой частное двух выражений: u=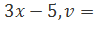 4
4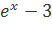 . По формуле 5: y′=
. По формуле 5: y′=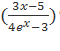 =
=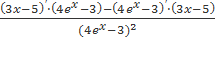 =
=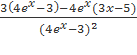
4. ![]()
Решение. Найдем производную данной функции по правилу дифференцирования сложной функции (формула 6):
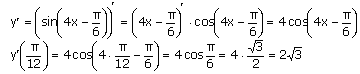
5. Если ![]() , то
, то 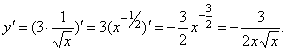
6. y = x3 – 3x2 + 5x + 2. Найдем y '(–1).
y ' = 3x2 – 6x+ 5. Следовательно, y '(–1) = 14.
7.Если y = ln x · cos x, то y ' = (ln x) ' cos x + ln x (cos x) ' =1/x∙cos x – ln x · sin x.
8. 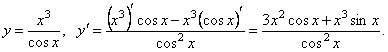
Пусть дана функция. Для её исследования нужно:
1) Найти её область определения. Если это не слишком сложно, то полезно найти также область значений. (Однако, во многих случаях, вопрос нахождения откладывается до нахождения экстремумов функции.)
2) Выяснить общие свойства функции, которые помогут в определении её поведения: не является ли функция чётной либо нечётной, не является ли она периодической.
3) Выяснить, как ведёт себя функция при приближении аргумента к граничным точкам области определения, если такие граничные точки имеются. Если функция имеет точки разрыва, то эти точки тоже проверить на наличие вертикальных асимптот функции. Найти наклонные асимптоты.
4) Найти точки пересечения графика с осями координат, что состоит в простом вычислении значения функции при условии:
С осью ОX: y=0;
С осью ОY: x=0.
Нахождение точек пересечения с осью может привести к необходимости решить сложное алгебраическое уравнение, что, быть может, удастся сделать лишь приближённо. Отыскав корни функции и точки разрыва, мы можем определить знак функции на каждом из интервалов между этими точками. Это можно сделать либо вычислив значение функции в какой-нибудь из точек интервала, либо применив метод интервалов.
5)Найти промежутки монотонности. Для этого находят производную и решают неравенство:
![]() . На промежутках, где это неравенство выполнено, функция возрастает. Там, где выполнено неравенство
. На промежутках, где это неравенство выполнено, функция возрастает. Там, где выполнено неравенство ![]() , функция убывает.
, функция убывает.
Найдя интервалы монотонности, мы можем сразу определить точки локального экстремума: там, где возрастание сменяется убыванием, располагаются локальные максимумы, а там, где убывание сменяется возрастанием - локальные минимумы.
6) Нахождение интервалов выпуклости и вогнутости ведётся с помощью второй производной. Найдя ![]() , мы определяем знаки
, мы определяем знаки ![]() на интервалах:
на интервалах:
если ![]() ›0, то кривая графика функции вогнута;
›0, то кривая графика функции вогнута;
если ![]() ‹0, то кривая графика функции выпуклая.
‹0, то кривая графика функции выпуклая.
Заодно определяем точки перегиба как те точки, в которых функция меняет направление выпуклости (и непрерывна).
7) Нахождение точек пересечения графика с асимптотой и дополнительных точек. Этот пункт не носит обязательного характера, однако нахождение таких точек придаёт исследованию функции и построенному её графику законченность и полноту.
Заметим, что получающиеся в процессе исследования функции точки на осях координат и на графике полезно сразу же наносить на чертёж. Это помогает по ходу дела уяснять вид графика.
3. Выполните самостоятельно:
№ варианта | Найти производную функции y: | № варианта | Найти производную функции y: |
1 | 1. y=6 2. y= 3. y= 4. y= 5. y= | 6 | 1. y=-6 2. y= 3. y= 4. y= 5. y= |
2 | 1. y=-7 2. y= 3. y= 4. y=ln(6x-3) 5. y= | 7 | 1. y=-7 2. y= 3. y= 4. y=ln(6x-3) 5. y= |
3 | 1.y=4x-3tgx+6x-8 2. y= 3.y= 4.y= 5.y= | 8 | 1.y=-5x+2ctgx+3x-2 2. y= 3.y= 4.y= 5.y= |
4 | 1. y=7x-9 2. y= 3. y= 4. y= 5. y= | 9 | 1. y=-5x-7 2. y= 3. y= 4. y= 5. y= |
5 | 1.y=6lnx-3,6 2. y=(3x-4)· 3.y= 4.y=( 5.y= | 10 | 1.y=16x-0,6 2. y=(7x-9)· 3.y= 4.y=( 5.y= |
4.Выполните самостоятельно:
Вариант №1 Исследовать функцию на монотонность и экстремум: 1. y= 2. y= | Вариант №2 Исследовать функцию на монотонность и экстремум: 1. y= 2. y= |
Вариант №3 Исследовать функцию на монотонность и экстремум: 1. y= 2. y= | Вариант №4 Исследовать функцию на монотонность и экстремум: 1. y= 2. y= |
Вариант №5 Исследовать функцию на монотонность и экстремум: 1. y= 2. y= | Вариант №6 Исследовать функцию на монотонность и экстремум: 1. y= 2. y= |
Вариант №7 Исследовать функцию на монотонность и экстремум: 1. y= 2. y= | Вариант №8 Исследовать функцию на монотонность и экстремум: 1. y= 2. y= |
Вариант №9 Исследовать функцию на монотонность и экстремум: 1. y= 2. y= | Вариант №10 Исследовать функцию на монотонность и экстремум: 1. y= 2. y= |
5. Контрольные вопросы:

|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 |




 .
.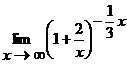 .
.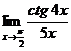 .
.