Математическое ожидание квадрата отклонения случайной величины X от ее метематического ожидания М(X)называют дисперсией случайной величины X и обозначают D(x), т. е. D(x)=М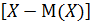 2 (2)
2 (2)
Размерность дисперсии равна квадрату случайной величины и ее неудобно использовать для характеристики разброса, поэтому удобнее применять корень квадратный из дисперсии – среднее квадратическое отклонение. Эта величина дает представление о размахе колебаний случайной величины около математического ожидания.
σ(сигма)=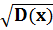 (3)
(3)
Пример 2
Найти математическое ожидание дискретной случайной величины X, зная закон её распределения.
x | -1 | 0 | 1 | 2 | 3 |
Р | 0,05 | 0,2 | 0,4 | 0,3 | 0,05 |
Решение: по формуле (1):
М(X)=-1·0,05+0·0,2+1·0,4+2·0,3+3·0,05=1,1
Пример 3
Дискретная случайная величина X имеет закон распределения
x | 0 | 1 | 2 |
Р | 0,3 | 0,5 | 0,2 |
Найти дисперсию и среднее квадратичное отклонение X.
1) М(X)=0·0,3+1·0,5+2·0,2=0,7
x | pi |
|
|
|
|
-1 0 1 2 | 0,1 0,3 0,4 0,2 | -0,1 0 0,4 0,4 | -1,7 -0,7 0,3 1,3 | 2,89 0,49 0,09 1,69 | 0,289 0,147 0,036 0,338 |
Σ | 1 | 0,7 | 0,81 |
2) Из таблицы следует D(X)=0,81
3) σ(X)=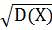 =
=![]() =0,9
=0,9
Выполните самостоятельно:
Вариант 1 Случайная величина X задана законом распределения:
Найти математическое ожидание М(X), дисперсию D(X) и среднее квадратичное отклонение σ(X). | Вариант 2 Случайная величина X задана законом распределения:
Найти математическое ожидание М(X), дисперсию D(X) и среднее квадратичное отклонение σ(X). | ||||||||||||||||||||
Вариант 3 Случайная величина X задана законом распределения:
Найти математическое ожидание М(X), дисперсию D(X) и среднее квадратичное отклонение σ(X). | Вариант 4 Случайная величина X задана законом распределения:
Найти математическое ожидание М(X), дисперсию D(X) и среднее квадратичное отклонение σ(X). | ||||||||||||||||||||
Вариант 5 Случайная величина X задана законом распределения:
Найти математическое ожидание М(X), дисперсию D(X) и среднее квадратичное отклонение σ(X). | Вариант 6 Случайная величина X задана законом распределения:
Найти математическое ожидание М(X), дисперсию D(X) и среднее квадратичное отклонение σ(X). |
Подведение итогов практической работы.
Контрольная работа для итогового контроля знаний
Практическая работа №10
Контрольная работа по теме «Основы теории вероятностей и математической статистики»
Вариант 1
№1.
В группе 20 студентов, среди них 14 юношей. Найти вероятность того, что среди наудачу выбранных 6-ти студентов будут 3 девушки и 3 юноши.
№2.
Имеются 4 коробки с шарами.
1-я: 4 синих и 5 красных;
2-я: 5 синих и 4 красных;
3-я: 7 красных;
4-я: 12 синих.
Наудачу берут шар. Он красный. Найти вероятность того, что он из 2-й коробки.
№3
Двум студентам предложена задача. Вероятность того, что её решит 1-й студент равна 0,72, что решит 2-й – 0,65. Найти вероятность того, что задачу решат оба студента; что решит только один?
№4
Случайная величина X задана законом распределения:
| 2 | 3 | 10 |
| 0,1 | 0,4 | 0,5 |
Найти математическое ожидание М(X), дисперсию D(X) и среднее квадратичное отклонение σ(X).
Вариант 2
№1
Имеются 23 детали и среди них 19 стандартные. Случайным образом выбирают сразу 6. Какова вероятность, что среди выбранных ровно 5 стандартных?
№2
В цехе продукция производится на 3-х станках:
1-й станок 45% всей продукции, из них брак 5%;
2-й станок 35% всей продукции, из них брак 10%;
3-й станок 20% всей продукции, из них брак 2%.
Найти вероятность, что наудачу взятая деталь из всех произведенных стандартная. Какова вероятность, что она была произведена на 1-м станке?
№3
Два стрелка независимо друг от друга производят выстрел по мишени. Вероятность попадания 1-м -
0,8, 2-м – 0,9. Какова вероятность, что после одного выстрела в мишени будет только одна пробоина?
№4
Случайная величина X задана законом распределения:
| 0,1 | 2 | 10 | 20 |
| 0,4 | 0,2 | 0,15 | 0,25 |
Найти математическое ожидание М(X), дисперсию D(X) и среднее квадратичное отклонение σ(X).
Вариант 3
№1
В урне лежат шары: 7 белых, 4 черных и 9 красных. Наудачу вынимают сразу два шара. Какова вероятность, что они окажутся одного цвета?
№2 Какова вероятность, что при десяти бросках игральной кости пять очков выпадут ровно 3 раза?
№3
Цех производит продукцию на 2-х станках:
70% изготавливается на 1-м станке, среди них 12% составляют бракованные детали, остальные детали производятся на втором станке, среди них 15% бракованные. Какова вероятность, что наудачу взятая деталь окажется бракованной? Какая вероятность, что бракованная деталь произведена на 2-м станке?
№4
Случайная величина X задана законом распределения:
| -1 | 1 | 2 | 3 |
| 0,48 | 0,01 | 0,09 | 0,42 |
Найти математическое ожидание М(X), дисперсию D(X) и среднее квадратичное отклонение σ(X).
Вариант 4
№1
Три стрелка стреляют независимо друг от друга по цели. Вероятность попадания 1-м -0,8; 2-м – 0,75; 3-м – 0,7. Найти вероятность того, что будет:
1) хотя бы одно попадание;
2) ровно одно попадание;
если произведен один выстрел каждым.
№2
В магазин поступают часы, выпускаемые на 3-х заводах. Первый завод поставляет 40%, второй – 45%, третий – 15%. В продукции первого завод 20% часов спешат, второго завода – 30% часов спешат, третьего – 10% спешат. Найти вероятность того, что купленные часы спешат?
№3
Какова вероятность, что при десяти бросках игральной кости пять очков выпадут ровно 3 раза?
№4
Случайная величина X задана законом распределения:
| -1 | 1 | 2 | 3 |
| 0,19 | 0,51 | 0,25 | 0,05 |
Найти математическое ожидание М(X), дисперсию D(X) и среднее квадратичное отклонение σ(X).
Вариант 5
№1
Найти вероятность того, что при 10 бросках игральной кости, 6 очков выпадет ровно 5 раз?
№2
Детали на сборку попадают из трёх автоматов. Известно, что первый автомат дает 3% брака, второй – 2% брака, третий – 4% брака. Найти вероятность попадания на сборку бракованной детали, если 1-й автомат произвел 1000 деталей, 2-й – 2000 деталей и 3-й – 2500 деталей. Какова вероятность, что бракованная деталь произведена на 2-м автомате?
№3
Из 3000 лотерейных билетов выигрышными являются 12. Какова вероятность, что из наудачу взятых 15 билетов хоть один будет с выигрышем?
№4
Случайная величина X задана законом распределения:
| 3 | 5 | 2 |
| 0,1 | 0,6 | 0,3 |
Найти математическое ожидание М(X), дисперсию D(X) и среднее квадратичное отклонение σ(X).
Вариант 6
№1
В белом ящике 12 красных и 6 синих шаров, в желтом ящике 15 красных и 10 синих шаров. Наудачу из некоторого ящика выбирают шар. Какая вероятность, что он красный? Какова вероятность, что красный шар вынут из белого ящика?
№2 Что вероятнее выиграть у равносильного противника 4 партии из 6-ти или 2 из 3-х?
№3
Два студента решают задачу независимо друг от друга. Вероятность того, что решит 1-й – 0,7, что решит 2-й – 0,8. Найти вероятность того, что:
а) решат оба;
б) решит только один?
№4
Случайная величина X задана законом распределения:
| 2 | 3 | 5 |
| 0,1 | 0,6 | 0,3 |
Найти математическое ожидание М(X), дисперсию D(X) и среднее квадратичное отклонение σ(X).

|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 |




