1. Сформулируйте правила нахождения производной суммы, произведения, частного.
2. Как найти производную сложной функции?
3. Как применяется производная функции для исследования функции на монотонность, экстремум?
Практическая работа №3
Контрольная работа по теме:
««Применение дифференциального исчисления
к исследованию функций»
Вариант№1 Исследовать функцию и построить график: 3. y= 4. y= | Вариант№2 Исследовать функцию и построить график: 3. y= 4. y= |
Вариант№3 Исследовать функцию и построить график: 3. y= 4. y= | Вариант№4 Исследовать функцию и построить график: 3. y= 4. y= |
Вариант№5 Исследовать функцию и построить график: 3. y= 4. y= | Вариант№6 Исследовать функцию и построить график: 3. y= 4. y= |
Вариант№7 Исследовать функцию и построить график: 3. y= 4. y= | Вариант№8 Исследовать функцию и построить график: 3. y= 4. y= |
Вариант№9 Исследовать функцию и построить график: 3. y= 4. y= | Вариант№10 Исследовать функцию и построить график: 3. y= 4. y= |
Вариант№11 Исследовать функцию и построить график: 1. y= 2. y= | Вариант№12 Исследовать функцию и построить график: 5) y= 6) y= |
Практическая работа № 4.
Тема: Вычисление неопределённых интегралов.
Вычисление определённых интегралов различными методами.
Цель: Проверить на практике знание понятия неопределённого и определенного интегралов, умение вычислять табличные интегралы, умение вычислять определенный интеграл методом введения новой переменной и по частям.
Обеспечение практической работы:
Теоретический материал методической рекомендации к практической работе.
Учебник. «Математика». – М.: Дрофа, 2010.
Математика. М:Форум-Инфа 2008.
Индивидуальные карточки с вариантом практической работы.
1.Теоретический материал и примеры вычисления неопределённого интеграла методом введения новой переменной.
1.1Неопределённый интеграл и непосредственное интегрирование.
Непосредственное интегрирование – это нахождение неопределенных интегралов с использованием таблицы интегралов и свойств неопределенного интеграла:
1.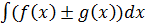 =
=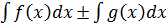
2.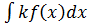 =k
=k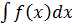 , где k=const
, где k=const
Таблица интегралов
1 |
| 11 |
|
2 |
| 12 |
|
3 |
| 13 |
|
4 |
| 14 |
|
5 |
| 15 |
|
6 |
| 16 |
|
7 |
| 17 |
|
8 |
| 18 |
|
9 |
| 19 |
|
10 |
| 20 |
|
1.2 Замена переменной в неопределённом интеграле
(интегрирование подстановкой).
![]() Пусть
Пусть ![]() . Тогда
. Тогда ![]() . Здесь t(x) - дифференцируемая монотонная функция.
. Здесь t(x) - дифференцируемая монотонная функция.![]() При решении задач замену переменной можно выполнить двумя способами.
При решении задач замену переменной можно выполнить двумя способами. ![]() 1. Если в подынтегральной функции удаётся сразу заметить оба сомножителя, и f(t(x)), и
1. Если в подынтегральной функции удаётся сразу заметить оба сомножителя, и f(t(x)), и ![]() , то замена переменной осуществляется подведением множителя
, то замена переменной осуществляется подведением множителя ![]() под знак дифференциала:
под знак дифференциала: ![]() , и задача сводится к вычислению интеграла
, и задача сводится к вычислению интеграла ![]() . Например,
. Например, ![]() (задача сведена к вычислению
(задача сведена к вычислению ![]() , где t = cos x)
, где t = cos x) ![]() (аналогично находится интеграл от
(аналогично находится интеграл от ![]() );
); ![]() (задача сведена к вычислению
(задача сведена к вычислению ![]() , где t = sin x)
, где t = sin x) ![]() .
.
![]() 2. Замену переменной можно осуществлять формальным сведением подынтегрального выражения к новой переменной.
2. Замену переменной можно осуществлять формальным сведением подынтегрального выражения к новой переменной.
![]() Пример 1.
Пример 1.
![]()
![]() имеет смысл перейти к переменной (сделать подстановку) t = sin x. Выражаем все множители подынтегрального выражения через переменную t:
имеет смысл перейти к переменной (сделать подстановку) t = sin x. Выражаем все множители подынтегрального выражения через переменную t: 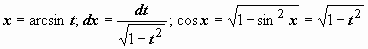 ; в результате
; в результате ![]()
![]() (возвращаемся к исходной переменной)
(возвращаемся к исходной переменной) ![]() . Другие примеры:
. Другие примеры: 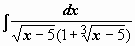 . Подынтегральная функция содержит два множителя, ни один из которых не является производной другого, поэтому подводить их под знак дифференциала бесполезно. Попытаемся ввести новую переменную, такую, чтобы корни извлеклись:
. Подынтегральная функция содержит два множителя, ни один из которых не является производной другого, поэтому подводить их под знак дифференциала бесполезно. Попытаемся ввести новую переменную, такую, чтобы корни извлеклись: 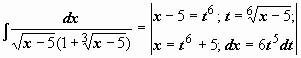 =
= 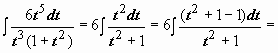
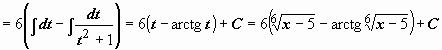
![]() Пример 2.
Пример 2.
![]()
![]()
![]() (интеграл №19 из табл.). Здесь подынтегральная функция состоит из единственного множителя; можно опять попытаться сделать такую замену переменной, чтобы корень извлёкся. Структура подкоренного выражения подсказывает эту замену:
(интеграл №19 из табл.). Здесь подынтегральная функция состоит из единственного множителя; можно опять попытаться сделать такую замену переменной, чтобы корень извлёкся. Структура подкоренного выражения подсказывает эту замену: ![]() (или
(или ![]() ,
, ![]() ):
): 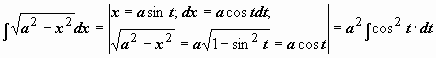 . Интеграл свёлся к интегралу от квадрата косинуса. При интегрировании чётных степеней синуса и косинуса часто применяются формулы, выражающие
. Интеграл свёлся к интегралу от квадрата косинуса. При интегрировании чётных степеней синуса и косинуса часто применяются формулы, выражающие ![]() и
и ![]() через косинус двойного угла:
через косинус двойного угла: ![]() .
. ![]() Поэтому
Поэтому ![]()
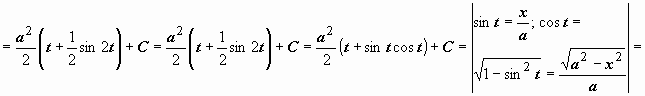
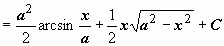 .
.
Пример 3.
![]()
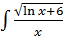 dx=
dx=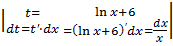 =
=![]() dt=
dt=![]() dt=
dt=![]() +С=
+С=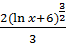 +С
+С
![]() 1.3 Интегирование по частям:
1.3 Интегирование по частям:
![]() Производится по формуле :
Производится по формуле :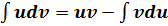
![]() Пример 4.
Пример 4.
![]()
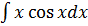 =
=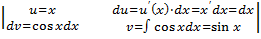 =x·
=x·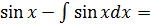 =x·
=x·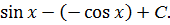
![]()
![]() Пример 5.
Пример 5.
![]()
![]()
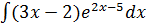 =
=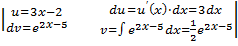 =
=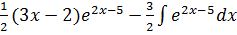 =
=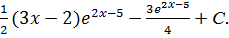
![]() Пример 6.
Пример 6.
![]()
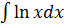 =
=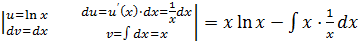 =
=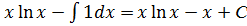 .
.
2. Определенный интеграл, его свойства и вычисление
2.1. Определенный интеграл вычисляется по формуле Ньютона-Лейбница:
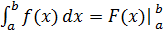 = F(a)-F(b)
= F(a)-F(b)
![]() - соответственно верхний и нижний пределы интегрирования, они пишутся и читаются снизу вверх, а в формулу подставляются сверху вниз!)
- соответственно верхний и нижний пределы интегрирования, они пишутся и читаются снизу вверх, а в формулу подставляются сверху вниз!)
Основные свойства определенного интеграла:
1. При перестановке пределов интегрирования изменяется знак интеграла:
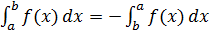
2. Отрезок интегрирования можно разбивать на части:
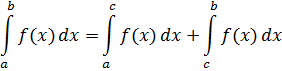
3. Определенный интеграл от алгебраической суммы функций равен алгебраической сумме их определенных интегралов.
4. Постоянный множитель можно выносить за знак интеграла.
Пример 1.
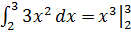 =
=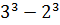 =27-8=19.
=27-8=19.
2.2 Вычисления определённого интеграла методом введения новой переменной.
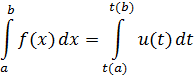
Пример 2.
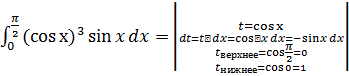 =
=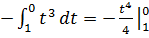 =
=![]() =
=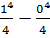 =
=
Пример 3.
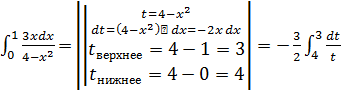 = -
= - 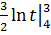 =-
=- (
(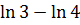 )=-
)=-![]()
1.3 Вычисление определенного интеграла по частям:
Используем формулу:
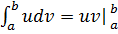 -
-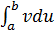
Пример 4.
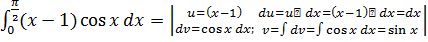 =
=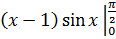 -
-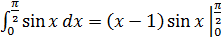 +
+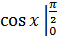 =(
=(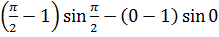 )+
)+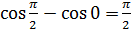 -1-1=
-1-1= -2;
-2;
Пример 5.
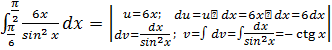 =-6xctgx
=-6xctgx![]() +
+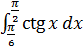 =-6·
=-6·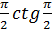 -6·
-6·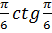 +ln|sinx|
+ln|sinx|![]() =π
=π![]() + ln|sin
+ ln|sin |- ln|sin
|- ln|sin |= π
|= π![]() + ln1- ln
+ ln1- ln = π
= π![]() + 0+ln2= π
+ 0+ln2= π![]() +ln2
+ln2
3. Выполните самостоятельную работу:
1) Найдите неопределенный интеграл:
![]()
№1 1. 2. 3. 4. 5. | №2 1. 2. 3. 4. 5. | №3 1. 2. 3. 4. 5. |
№4 1. 2. 3. 4. 5. | №5 1. 2. 3. 4. 5. i. | №6 1. 2. 3. 4. 5. |
№7 1. 2. 3. i. ii. 4. 5.
| №8 1. 2. 3. 4. 5. | №9 1. 2. 3. 4. 5. |
№10 1. 2. 3. 4. 5. | №11 1. 2. 3. 4. 5.
| №12 1. 2. 3. 4. 5. |
№13 1. 2. 3. 4. 5. | №14 1. 2. 3. 4. 5. | №15 1. 2. 3. 4. 5. |
2) Вычислите определенный интеграл.

|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 |




