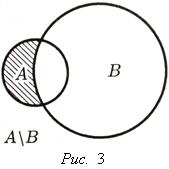
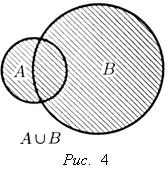
Объединением множеств A и B называется множество А⋂В(см. рис. 4) ![]()
![]()
![]()
Аналогично, если ![]()
![]() подмножества множества ℐ, то их объединением будет множество
подмножества множества ℐ, то их объединением будет множество
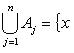
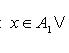
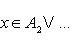
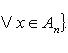
Пересечением подмножеств A и B называется множество (см. рис. 5)
![]()
![]()
![]()
![]()
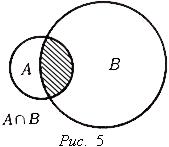
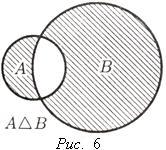
Рисунки 1-6 называются диаграммы Эйлера-Венна.
Аналогично, символом ![]()
![]() обозначают пересечение подмножеств
обозначают пересечение подмножеств ![]()
![]() множества ℐ,т. е.
множества ℐ,т. е. 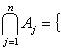
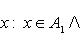
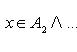
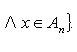
Два элемента a и b называются упорядоченной парой, если указано, какой из этих элементов первый, какой второй, при этом
![]()
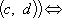
![]()
![]()
Упорядоченную пару элементов a и b обозначают символом (a, b).
Аналогично определяется упорядоченная система из n элементов a1, a2, ..., an, которую обозначают символом (a1, a2, ..., an). Элементы a1, a2, ..., an называются координатами упорядоченной системы (a1, a2, ..., an).
Совокупность всевозможных упорядоченных пар (a, b), где, называется произведением множеств A и B и обозначается символом ![]() .
.
Аналогично, символом обозначают произведение множеств, т. е. совокупность всевозможных упорядоченных систем (a1, a2, ..., an),
где ![]()
![]()
![]() .
.
3. Свойства операций над множествами
Пусть A, B и D - произвольные подмножества множестваℐ . Тогда непосредственно из определений объединения, пересечения и дополнения вытекают следующие предложения:
1. Закон идемпотентности для объединения и пересечения множеств:
А⋃А=А, А⋂А=А
2. Закон коммутативности:
А⋃В=В⋃А; А⋂В=В⋂А.
3. Закон ассоциативности:
А⋃(В⋃D)= (А⋃В)⋃D; А⋂(В⋂D)= (А⋂В)⋂D
4. Закон дистрибутивности:
А⋂(В⋃D)=(А⋂В)⋃(А⋂D); А⋃(В⋂D)=(А⋃В)⋂(А⋃D)
5. Закон поглощения:
А⋃(В⋂D)=А, А⋂(А⋃D)=А
6. Закноны, описывающие свойства пустого и универсального множества по отношению к объединению и пересечению:
А⋃∅=А, А⋂∅=∅, А⋃ℐ=ℐ, А⋂ℐ=А
7. Законы дополнения: А⋃![]() =ℐ, А⋂
=ℐ, А⋂![]() =∅
=∅
8. Закон инволютивности дополнения: ![]() =А
=А
9. Закон Де Моргана: ![]() =
=![]() ,
, ![]() =
=![]()
Истинность каждого тождества проще всего проверяется построением диаграмм Эйлера-Венна.
4. Выполните самостоятельно:
проверку следующих утверждений диаграммой Эйлера-Венна:
Вариант 1 |
|
Вариант 2 |
|
Вариант 3 |
|
5. Подведение итогов практического занятия.
Практическая работа №8
Тема: Вычисление вероятностей случайных событий. Формула полной вероятности
Цель: приобретение базовых знаний в области фундаментальных разделов математики. Повторить и систематизировать знания по данной теме.
Задачи:
• развитие творческого профессионального мышления;
• познавательная мотивация;
• овладение языком науки, навыки оперирования понятиями;
• овладение умениями и навыками постановки и решения задач;
• углубление теоретической и практической подготовки;
• развитие инициативы и самостоятельности студентов.
Теоретические сведения:
1. Приведите примеры: 1) достоверных событий; 2) невозможных событий; 3) случайных событий.
2. Что вероятнее — появление герба при бросании монеты или появление нечетного числа очков при бросании игральной кости?
3. Что вероятнее при бросании двух монет — выпадение двух цифр или цифры и герба?
4. Что вероятнее получить при делении домино между 4 игроками — все «дубли» или же все кости с «шестерками»?
5. Проведите следующий эксперимент: бросьте 50 раз две игральные кости и запишите сумму для каждого броска. Какая сумма появилась чаще всего? Какая реже всего? Какое число очков появилось чаще: 3 или 12?
6. Из мешка с 33 жетонами, на которых написаны русские буквы, вытаскивают один за другим 4 жетона. Сколько раз, по вашему мнению, нужно повторить этот эксперимент, чтобы из этих букв получилось слово «барс»? Во сколько раз будет меньше число необходимых экспериментов, если 4 жетона вытаскивают сразу (т. е. порядок их появления несуществен)?
7. Что вероятнее — угадать 6 номеров из 49 или 5 номеров из 36?
8. При 10 бросаниях правильной монеты выпадал герб. Что вероятнее при следующем броске — выпадение цифры или герба?
2. Опыт, испытание. Основным понятием, с которым мы будем иметь дело в дальнейшем, является понятие опыта, или испытания. Этому понятию нельзя дать математическое определение, однако ясно, что значат слова «подбросим монету и посмотрим, упала она вверх гербом или цифрой» или «включить электрическую лампочку и поглядеть, через какое время она перегорит». Для нас будет существенно лишь то, что данное испытание может иметь различные исходы. При этом для простоты будем рассматривать лишь случаи, когда множество этих исходов конечно и равно n. С каждым опытом можно связать различные множества исходов. Важно лишь то, что при каждом испытании происходит один и только один исход.
Пример 1. При бросании игральной кости возможны следующие исходы:
1) А1, А2, А3, А4, А5, А6 это означает выпадение очков от 1 до 6 включительно;
2) В1 — выпадение нечетного числа очков, а В2 — выпадение четного числа очков;
Пример 2. При бросании монеты возможны исходы А1 – выпал герб, А2 – выпала «решка»
Пример 3. Произведен выстрел по мишени: А1 – попадание, А2 – промах.
Введем следующее определение:
Определение. Событием при данном испытании называется любое подмножество X множества U исходов.
В дальнейшем, говоря об исходах, из которых состоит событие X, мы будем говорить, что они благоприятствуют этому событию. Про остальные же исходы будем говорить, что они не благоприятствуют событию X.
Определение 2. Вероятностью события X называют сумму вероятностей исходов, благоприятствующих этому событию.
Пример 1. Бросают игральную кость, событие А – выпадение четного числа очков. Ему благоприятствуют случаи А2, А4, А6, т. о. 3 исхода из 6-ти возможных.
Пример 2. Бросают монету, событие В – выпадение герба, ему благоприятствует один исход из двух возможных.
Если испытание может привести к одному и только одному из n различных равновозможных исходов и если m из этих исходов благоприятствуют появлению события А определяется формулой
Р(А)=m/n
Это классическое определение вероятности.
Основные свойства:
1. Вероятность любого события заключена между 0 и единицей: 0≤ Р(А)≤ 1
2. Вероятность достоверного события U, т. е. такое событии обязательно произойдет при испытании: Р(U)=1
3. Вероятность испытание невозможного события V равна нулю: Р(V)=0
4. Сумма вепроятностей двух противоположных событий А и Ā, т. е. таких событий, что появление одного из них исключает появление другого, равна единице:
Р(А)+Р(Ā)=1
Пример 1.
Из урны, в которой находится 4 белых, 9 черных, 7 красных шаров. Наудачу вынимают один шар. Какова вероятность, что этот шар белый?
Решение:
Элементарным исходом является извлечение любого шара. Число таких исходов равно числу шаров: 4+9+7=20, т. е. n=20. Событие А – извлечение белого шара, ему благоприятствуют 4 исхода, т. к. белых шаров 4, значит m=4, поэтому по формуле Р(А)=m/n находим: Р(А)=4/20=1/5=20%
Пример 2. Задача о выборке.
В партии из S деталей имеются Т нестандартных. Определить вероятность того, что среди выбранных наудачу p деталей нестандартными окажутся ровно t деталей.
Решение:
Элементарным исходом является выборка любых p изделий из общего числа S. Число таких исходом равно числу сочетаний из S по p, т. е.n=![]()
Интересующее нас событие А – это извлечение p деталей, из которых t нестандартные. Следовательно, благоприятными для А являются такие группы по p изделий, в которых p-t изделий – качественные, а t – нестандартные.
Число таких групп
m=![]() ·
·![]() , где
, где 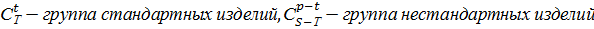 , причем события из группы стандартных комбинируются из группы нестандартных, тогда
, причем события из группы стандартных комбинируются из группы нестандартных, тогда
Р(А)=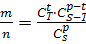
§ 2. ТЕОРЕМЫ СЛОЖЕНИЯ И УМНОЖЕНИЯ ВЕРОЯТНОСТЕЙ
Суммой нескольких событий называется событие, состоящее в появлении хотя бы одного из этих событий.
Произведением нескольких событий называется событие, состоящее в совместном осуществлении всех этих событий.
Теорема сложения вероятностей.
Если события Ах, А2, ... , А п несовместны, т. е. никакие два из них не могут осуществиться вместе, то
P(А1+ А2+ ...+ Ап) = Р (A1) + Р(А2) + ... + Р(Аn) (1)
Вероятность события А, вычисленная в предположении, что произошло событие В, называется условной вероятностью события А при условии В {обозначается Р (А/В).
Теорема умножения вероятностей.
Вероятность произведения нескольких независимых событий равна произведению вероятности этих событий:
Р(А1А2 ... Аn) = = Р (A1)·P (А2) ·Р(А3) ... Р (Аn ) (2)
(события А1, А2, ..., Ап независимы, т. е. осуществление любого числа из них не меняет вероятностей осуществления остальных).
Пример 3. В партии из 50 изделий содержится пять бракованных. Какова вероятность того, что из выбранных наудачу 30 изделий не более одного бракованного?
Решение. Пусть А — событие, состоящее в том, что 30 изделий выборки — качественные, В — в рассматриваемой выборке из 30 изделий только одно бракованное, С— не более одного бракованного. Тогда, очевидно, С = А + В. Так как события А и В несовместны, то по формуле (1) имеем
Р(С) = Р(А) + Р(В).
Найдем вероятности событий А и В:
Р(А)= ≈ 0,007 Р(В)= ≈0,065
Отсюда Р(С)≈ 0,072
Пример 4. Два станка работают независимо друг от друга. Вероятность бесперебойной работы первого станка в течение некоторого времени t равна p1= 0,9, второго — р2= 0,8. Какова вероятность бесперебойной работы обоих станков в течение указанного промежутка времени?
Решение. Рассмотрим следующие события: A1 и А2— бесперебойная работа соответственно первого и второго станков в течение времени t; A — бесперебойная работа обоих станков в течение указанного времени. Тогда событие А есть совмещение событий А1 и А2, т. е. А = А1·A2. Так как события At и А2 независимы (станки работают независимо друг от друга), то по формуле (3) получим
Р(А) = Р(А1)·Р(А2) = 0,9·0,8 =0,72.
Пример 5. В примере 3 определить вероятность бесперебойной работы хотя бы одного из двух станков в течение времени t (событие В).
Решение. Первый способ. Рассмотрим противоположное событие В, означающее простой обоих станков в течение времени /. Очевидно, что событие В есть совмещение событий A1 и А2 простоев первого и второго станков, т. е. В = Ā1 ·Ā2. Так как события Ā1 и Ā2? независимы, то
Р(В) = Р (Ā1) .Р(Ā2) = ( 1- Р(А1))· ( 1- Р(А2)) = = 0,1·0,2 = 0,02.
Отсюда
Р{В) = 1 — Р(В) = 0,98.
Второй способ. Событие В происходит в том случае, когда имеет место одно из следующих трех несовместных событий: либо A1·Ā2—совмещение событий A1 4 и Ā2 (первый станок работает, второй — не работает), либо Ā1·А2— совмещение событий Ā1 и А2 (первый станок не работает, второй — работает), либо А1А2— совмещение событий А1 и Л2 (оба станка работают), т. е.
В = А1 Ā2+Ā1А2+ A1A2.
По формуле (1) получим
Р(В) = Р(А1 Ā2) + P(Ā1A2) + P(A1A2).
В силу того, что события A1 и А2, а следовательно, Ā1 и Ā2, независимы, имеем
Р(В)=Р(А1)·Р(Ā2)+Р(Ā1).Р(А2) + Р(А1)·Р(А2) = = Р(А1)[1-Р(А2)]+[1-Р(А1)]Р(А2) + Р(А1).Р(А2)=0,98.
Формула полной вероятности. Формула Байеса
Если с некоторым опытом связано п исключающих друг друга событий (гипотез)Н1 , Н2, ..., Нn и если событие А может осуществиться только при одной из этих гипотез, то вероятность события А вычисляется по формуле полной вероятности:
Р(А) = P(H1)P(A/H1) + Р(А2)Р(А/Н2) + ... + Р(Нп)Р(А/Нп).
После проведения опыта, в результате которого осуществилось событие А, вероятности гипотез Нi можно переоценить по формуле Байеса:
Р (Нi / А) = Р(Нi) · Р( А / Нi )
Р (А)
Пример 5. Имеется три урны с шарами. В первой урне 4 белых и 5 черных, во второй — 5 белых и 4 черных, в третьей — 6 белых шаров. Некто выбирает наугад одну из урн и вынимает из нее шар. Найти вероятность того, что: а) этот шар окажется белым; б) белый шар вынут из второй урны.
Решение, а) Пусть А — событие, означающее, что извлечен белый шар. Рассмотрим три гипотезы:
H1— выбрана первая урна; Н2— выбрана вторая урна ; Нз— третья. Так как урна, из которой извлекают шар, выбирается наугад, то
Р(Н1) = Р(Н2) = Р(Нз) = ⅓
Условные вероятности события А соответственно равны:
P(A/Н1) = 4/9 (вероятность извлечения белого шара из первой урны),
Р(А/Н2) = 5/9 (вероятность извлечения белого шара из второй урны),
Р(А/Н3) = 1 (вероятность извлечения белого шара из третьей урны).
а) Отсюда по формуле полной вероятности получим
Р(А)=1/3×4/9 + 1/3×5/9 + 1/3×1 = 2/3
б) Для определения вероятности того, что белый шар извлечен из второй урны, воспользуемся формулой Байеса:
Р{Н2 /А) = Р(Н2)Р(А/Н2) ‗ 1/3×5/9
P(A) 2/3
Схема повторных испытаний. Формула Бернулли
Если при одних и тех же условиях определенный опыт повторяется п раз и если вероятность появления некоторого события А в каждом опыте равна р, то вероятность того, что событие А в серии из п опытов произойдет ровно k раз, находится по формуле Бернулли:
Рn (k) = С рk q n-k, где q=1- р
Выполните самостоятельно:
Вариант 1 №1. В группе 20 студентов, среди них 14 юношей. Найти вероятность того, что среди наудачу выбранных 6-ти студентов будут 3 девушки и 3 юноши. №2. Имеются 4 коробки с шарами. 1-я: 4 синих и 5 красных; 2-я: 5 синих и 4 красных; 3-я: 7 красных; 4-я: 12 синих. Наудачу берут шар. Он красный. Найти вероятность того, что он из 2-й коробки. №3 Двум студентам предложена задача. Вероятность того, что её решит 1-й студент равна 0,72, что решит 2-й – 0,65. Найти вероятность того, что задачу решат оба студента; что решит только один? | Вариант 2 №1 Имеются 23 детали и среди них 19 стандартные. Случайным образом выбирают сразу 6. Какова вероятность, что среди выбранных ровно 5 стандартных? №2 В цехе продукция производится на 3-х станках: 1-й станок 45% всей продукции, из них брак 5%; 2-й станок 35% всей продукции, из них брак 10%; 3-й станок 20% всей продукции, из них брак 2%. Найти вероятность, что наудачу взятая деталь из всех произведенных стандартная. Какова вероятность, что она была произведена на 1-м станке? №3 Два стрелка независимо друг от друга производят выстрел по мишени. Вероятность попадания 1-м - 0,8, 2-м – 0,9. Какова вероятность, что после одного выстрела в мишени будет только одна пробоина? |
Вариант 3 №1 В урне лежат шары: 7 белых, 4 черных и 9 красных. Наудачу вынимают сразу два шара. Какова вероятность, что они окажутся одного цвета? №2 В автоколонне 12 машин. Вероятность выхода на линию каждой машины – 0,8. Найти вероятность, что работа автоколонны будет осуществляться без сбоев, если для этого требуется, чтоб не менее 10 машин вышли на линию? №3 Цех производит продукцию на 2-х станках: 70% изготавливается на 1-м станке, среди них 12% составляют бракованные детали, остальные детали производятся на втором станке, среди них 15% бракованные. Какова вероятность, что наудачу взятая деталь окажется бракованной? Какая вероятность, что бракованная деталь произведена на 2-м станке? | Вариант 4 №1 Три стрелка стреляют независимо друг от друга по цели. Вероятность попадания 1-м -0,8; 2-м – 0,75; 3-м – 0,7. Найти вероятность того, что будет: 1) хотя бы одно попадание; 2) ровно одно попадание; если произведен один выстрел каждым. №2 В магазин поступают часы, выпускаемые на 3-х заводах. Первый завод поставляет 40%, второй – 45%, третий – 15%. В продукции первого завод 20% часов спешат, второго завода – 30% часов спешат, третьего – 10% спешат. Найти вероятность того, что купленные часы спешат? №3 Какова вероятность, что при десяти бросках игральной кости пять очков выпадут ровно 3 раза? |
Вариант 5 №1 В мастерской работают 6 моторов. Для каждого мотора вероятность перегрева к обеденному перерыву равна 0,8. Найти вероятность того, что к обеденному перерыву перегреются: 1) ровно 4 мотора; 2) перегреются все моторы? №2 Детали на сборку попадают из трёх автоматов. Известно, что первый автомат дает 3% брака, второй – 2% брака, третий – 4% брака. Найти вероятность попадания на сборку бракованной детали, если 1-й автомат произвел 1000 деталей, 2-й – 2000 деталей и 3-й – 2500 деталей. Какова вероятность, что бракованная деталь произведена на 2-м автомате? №3 Из 3000 лотерейных билетов выигрышными являются 12. Какова вероятность, что из наудачу взятых 15 билетов хоть один будет с выигрышем? | Вариант 6 №1 В белом ящике 12 красных и 6 синих шаров, в желтом ящике 15 красных и 10 синих шаров. Наудачу из некоторого ящика выбирают шар. Какая вероятность, что он красный? Какова вероятность, что красный шар вынут из белого ящика? №2 По самолету противника производят три выстрела. Вероятность попадания при 1-м выстреле-0,5, при 2-м – 0,6, при 3-м – 0.8. Вероятность сбить самолет при условии попадания при 1-м выстреле – 0,3, при 2-м – 0,6 и при 3-м – 0,9. Найти вероятность того, что самолет будет сбит. Какова вероятность, что он будет сбит при 1-м выстреле? №3 Два студента решают задачу независимо друг от друга. Вероятность того, что решит 1-й – 0,7, что решит 2-й – 0,8. Найти вероятность того, что: а) решат оба; б) решит только один? |
Подведение итогов практической работы.
Практическая работа № 9
Тема: Вычисление числовых характеристик
Случайные величины
Случайной величиной называется величина, которая в результате опыта может принять любые заранее неизвестные значения. Различают дискретные и непрерывные случайные величины.
Дискретной случайной величиной называется такая, значение которой есть конечное или счетное множество фиксированных величин. Например, количество студентов, пришедших на лекцию, число бракованных изделий в партии продукции, число новорожденных за сутки. Для описания поведения дискретной случайной величины X задают все значения ![]() ,
,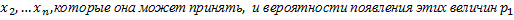 ,
,![]() .
.
Непрерывной называют такую случайную величину, которая может принимать любые значения в определенном интервале. Например, температура тела пациента за определенный промежуток времени; дальность полета футбольного мяча, объем утечки воды из городского водопровода.
Под законом распределением случайной величины мы будем понимать соответствие
«значение случайной величины ↔ вероятность принимать это значение».
Случайная величина считается заданной, если задан её закон распределения:
Значение случайной величины |
|
| … |
|
Вероятности значений |
|
| … |
|
Пример 1. Подбрасываем 1 раз кубик. Пусть X = {1, 2, 3, 4, 5, 6} количество очков, выпавшее при бросании кубика. Можно записать соответствие между значениями случайных величин x и p вероятностями принимать эти значения в виде «таблицы распределения вероятностей» или, коротко, «таблицы распределения»:
x | 1 | 2 | 3 | 4 | 5 | 6 |
Р | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 |
Рассмотрим случайниу величину ![]() =
=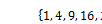 :
:
| 1 | 4 | 9 | 16 | 25 | 36 |
Р | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 |
При решении практических задач нет необходимости знать все возможные значения случайной величины и соответствующие им вероятности, а удобнее использовать такие количественные показатели, которые в сжатой форме достаточную информацию о случайной величине. Такие показатели называются числовыми характеристиками случайной величины. Основными из них являются: математическое ожидание, дисперсия и среднее квадратичное отклонение.
Математическое ожидание М(X) характеризует положение случайной величины на числовой оси, определяя некоторое среднее значение, около которого сосредоточены все возможные значения случайной величины.
М(X)=![]() +
+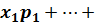
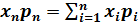 (1)
(1)
Дисперсия характеризует рассеяние (отклонение) случайной величины относительно математического ожидания.

|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 |




