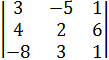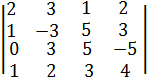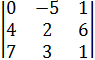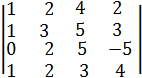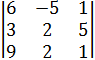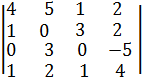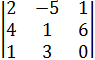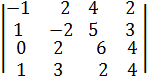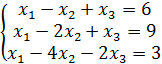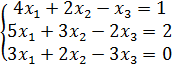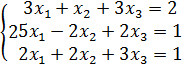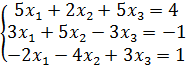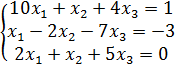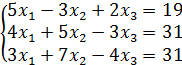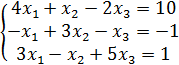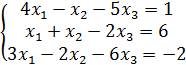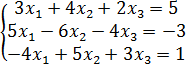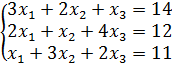Вариант 1 | Вариант 2 |
1. 2. 3. | 1. 2. 3. |
Вариант 3 | Вариант 4 |
1. 2. 3. | 1. 2. 3. |
Подведение итогов практической работы.
3.Контрольные вопросы:
1. Сформулируйте правила непосредственного интегрирования.
2. В каких случаях применяется способ интегрирования подстановкой?
3. Назовите формулу для интегрирования по частям. Что надо принять за u, а что за dv?
4. Что такое определенный интеграл. Напишите формулу Ньютона-Лейбница.
![]()
![]()
![]() Практическое занятие №5.
Практическое занятие №5.
![]() Тема: Вычисление определителей.
Тема: Вычисление определителей.
![]() Цель: приобретение базовых знаний в области фундаментальных разделов математики. Проверка усвоения знаний по вычислению определителей, выполнению операций над матрицами. Повторить и систематизировать знания по данной теме.
Цель: приобретение базовых знаний в области фундаментальных разделов математики. Проверка усвоения знаний по вычислению определителей, выполнению операций над матрицами. Повторить и систематизировать знания по данной теме.
![]() Задачи:
Задачи:
![]() • развитие творческого профессионального мышления;
• развитие творческого профессионального мышления;
![]() • познавательная мотивация;
• познавательная мотивация;
![]() • овладение языком науки, навыки оперирования понятиями;
• овладение языком науки, навыки оперирования понятиями;
![]() • овладение умениями и навыками постановки и решения задач;
• овладение умениями и навыками постановки и решения задач;
![]() • углубление теоретической и практической подготовки;
• углубление теоретической и практической подготовки;
![]() • развитие инициативы и самостоятельности студентов.
• развитие инициативы и самостоятельности студентов.
![]() Обеспечение практической работы:
Обеспечение практической работы:
![]() Теоретический материал методической рекомендации к практической работе.
Теоретический материал методической рекомендации к практической работе.
![]() Математика. М:Форум-Инфа 2008. , . Математика, – Серия: Среднее профессиональное образование. - Ростов-на-Дону «Феникс»,с.
Математика. М:Форум-Инфа 2008. , . Математика, – Серия: Среднее профессиональное образование. - Ростов-на-Дону «Феникс»,с.
![]() Щипачев вышей математики. - М.: Высшая школа, 2с.
Щипачев вышей математики. - М.: Высшая школа, 2с.
![]() , . Математика, – Серия: Среднее профессиональное образование. - Ростов-на-Дону «Феникс»,с.
, . Математика, – Серия: Среднее профессиональное образование. - Ростов-на-Дону «Феникс»,с.
![]() Индивидуальные карточки с вариантом практической работы.
Индивидуальные карточки с вариантом практической работы.
![]() Ход практического занятия.
Ход практического занятия.
![]() 1.Формулирование темы занятия, пояснение связи темы с другими темами учебной дисциплины;
1.Формулирование темы занятия, пояснение связи темы с другими темами учебной дисциплины;
![]() 2.Проверка готовности студентов к занятию;
2.Проверка готовности студентов к занятию;
![]() 3.Проведение непосредственно занятия согласно тематике и в соответствии с рабочей программой дисциплины:
3.Проведение непосредственно занятия согласно тематике и в соответствии с рабочей программой дисциплины:
![]() - Изучить теоретический материал по теме «Выполнение операций над матрицами. Вычисление определителей».
- Изучить теоретический материал по теме «Выполнение операций над матрицами. Вычисление определителей».
![]() - Рассмотреть примеры решения типовых заданий.
- Рассмотреть примеры решения типовых заданий.
![]() -Выполнить самостоятельную работу по вычислению определителей, выполнению действий над матрицами.
-Выполнить самостоятельную работу по вычислению определителей, выполнению действий над матрицами.
![]() - Ответить на контрольные вопросы.
- Ответить на контрольные вопросы.
![]()
![]() Теоретические сведения и методические рекомендации
Теоретические сведения и методические рекомендации
![]() по решению задач.
по решению задач.
![]()
![]() Определение. Матрицей из m строк, n столбцов называется прямоугольная таблица чисел
Определение. Матрицей из m строк, n столбцов называется прямоугольная таблица чисел 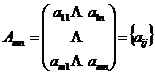 ;
; ![]() - элемент матрицы; i-номер строки; i=1,…,m; j-номер столбца, j=1,…,n; m, n – порядки матрицы. При m=n
- элемент матрицы; i-номер строки; i=1,…,m; j-номер столбца, j=1,…,n; m, n – порядки матрицы. При m=n ![]() - квадратная матрица.
- квадратная матрица.
![]() Определение. Определителем n-го порядка, соответствующим матрице
Определение. Определителем n-го порядка, соответствующим матрице ![]() , называется число
, называется число 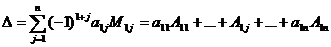 .
.
![]() Для вычисления определителя можно использовать элементы произвольной строки или столбца.
Для вычисления определителя можно использовать элементы произвольной строки или столбца.
![]() Определение. Алгебраическим дополнение
Определение. Алгебраическим дополнение ![]() элемента
элемента ![]() называется число, равное
называется число, равное 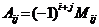 .
.
![]() Определение. Дополнительным минором
Определение. Дополнительным минором ![]() элемента
элемента ![]() матрицы
матрицы ![]() называется определитель матрицы n-1-го порядка, полученный из матрицы
называется определитель матрицы n-1-го порядка, полученный из матрицы ![]() вычеркиванием i-ой строки и j-го столбца.
вычеркиванием i-ой строки и j-го столбца.
![]()
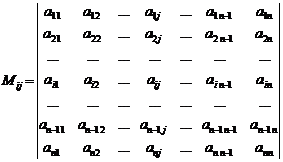 .
.
![]() Транспонирование матрицы – такое преобразование матрицы, при котором строки становятся столбцами с сохранением порядка следования.
Транспонирование матрицы – такое преобразование матрицы, при котором строки становятся столбцами с сохранением порядка следования.
![]() Свойства определителей.
Свойства определителей.
![]() При транспонировании матрицы определитель не меняется.
При транспонировании матрицы определитель не меняется.
![]() При перестановке любых двух строк (столбцов) определитель меняет только знак.
При перестановке любых двух строк (столбцов) определитель меняет только знак.
![]() При умножении строки (столбца) на некоторое число определитель умножается на это число.
При умножении строки (столбца) на некоторое число определитель умножается на это число.
![]() Если все соответствующие элементы квадратных матриц одного порядка одинаковы, за исключением элементов одной i-ой строки, то
Если все соответствующие элементы квадратных матриц одного порядка одинаковы, за исключением элементов одной i-ой строки, то 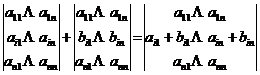 .
.
![]() Величина определителя не изменяется, если к элементам некоторой строки (столбца) прибавить соответствующие элементы другой строки (столбца), умноженной на некоторое число.
Величина определителя не изменяется, если к элементам некоторой строки (столбца) прибавить соответствующие элементы другой строки (столбца), умноженной на некоторое число.
![]() Определитель равен нулю, если
Определитель равен нулю, если
![]() - все элементы некоторой строки (столбца) равны нулю.
- все элементы некоторой строки (столбца) равны нулю.
![]() - две строки (столбца) одинаковы.
- две строки (столбца) одинаковы.
![]() - две строки (столбца) определителя пропорциональны.
- две строки (столбца) определителя пропорциональны.
![]() Методы вычисления определителей.
Методы вычисления определителей.
![]() 1). Разложение по строке или столбцу.
1). Разложение по строке или столбцу.
![]() 2). Метод обращения в нуль всех, кроме одного, элементов строки или столбца. Метод состоит в том, что с учетом свойств определителя при помощи какого-либо столбца (строки) путём умножения его на соответствующие числа и вычитания из остальных столбцов (строк), зануляются все элементы выбранной строки (столбца) кроме одного, принадлежащего вычитаемому столбцу (строке).
2). Метод обращения в нуль всех, кроме одного, элементов строки или столбца. Метод состоит в том, что с учетом свойств определителя при помощи какого-либо столбца (строки) путём умножения его на соответствующие числа и вычитания из остальных столбцов (строк), зануляются все элементы выбранной строки (столбца) кроме одного, принадлежащего вычитаемому столбцу (строке).
![]() 3). Метод приведения к треугольному виду. Алгоритм, предложенный в предыдущем пункте, используется для последовательного зануления всех элементов первой строки (столбца) кроме одного, второй строки (столбца) – всех кроме двух и т. д. В итоге определитель преобразуется к треугольному виду. Величина такого определителя равна произведению элементов главной диогонали.
3). Метод приведения к треугольному виду. Алгоритм, предложенный в предыдущем пункте, используется для последовательного зануления всех элементов первой строки (столбца) кроме одного, второй строки (столбца) – всех кроме двух и т. д. В итоге определитель преобразуется к треугольному виду. Величина такого определителя равна произведению элементов главной диогонали.
![]() 4). Вычисление с использованием теоремы Лапласа, согласно которой определитель
4). Вычисление с использованием теоремы Лапласа, согласно которой определитель ![]() - го порядка равен сумме произведений всех его миноров
- го порядка равен сумме произведений всех его миноров ![]() -го порядка, стоящих в выделенных
-го порядка, стоящих в выделенных ![]() строках (столбцах), на их алгебраические дополнения.
строках (столбцах), на их алгебраические дополнения.
![]() Примеры
Примеры
![]() 1. Вычислить данный определитель четвёртого порядка с помощью разложения по строке или столбцу:
1. Вычислить данный определитель четвёртого порядка с помощью разложения по строке или столбцу:
![]()
![]()
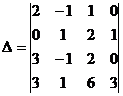
![]() Решение. Удобнее всего делать разложение по строке или столбцу, в которых встречается наибольшее число нулевых элементов. В данном случае – это четвёртый столбец. Итак имеем
Решение. Удобнее всего делать разложение по строке или столбцу, в которых встречается наибольшее число нулевых элементов. В данном случае – это четвёртый столбец. Итак имеем
![]()
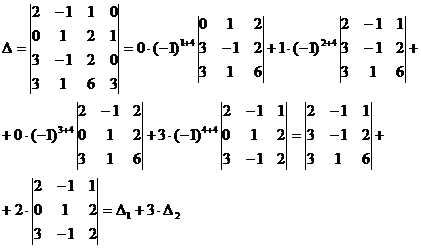
![]() Полученные в итоге два определителя третьего порядка вычислим тем же методом. В определителе
Полученные в итоге два определителя третьего порядка вычислим тем же методом. В определителе ![]() нулевых элементов нет, поэтому можно выбрать для разложения любой из столбцов, например, первый. В
нулевых элементов нет, поэтому можно выбрать для разложения любой из столбцов, например, первый. В ![]() единственный нулевой элемент находится на пересечении первого столбца со второй строкой. Для разнообразия будем разлагать
единственный нулевой элемент находится на пересечении первого столбца со второй строкой. Для разнообразия будем разлагать ![]() по второй строке:
по второй строке:![]()
![]()
![]()
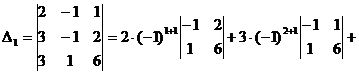
![]()
![]()
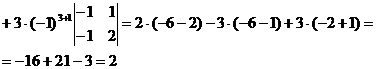
![]()
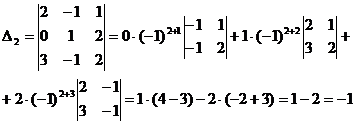
![]() Таким образом окончательно получим
Таким образом окончательно получим
![]()
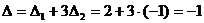
![]() 2. Используя метод обращения в нуль всех, кроме одного, элементов строки или столбца вычислить определитель матрицы
2. Используя метод обращения в нуль всех, кроме одного, элементов строки или столбца вычислить определитель матрицы
![]()
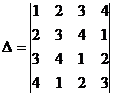
![]() Решение. Будем занулять все, кроме первого, элементы первой строки. С этой целью вычтем из второго, третьего и четвёртого столбцов первый столбец, умноженный соответственно на 2, 3 и 4. Получим
Решение. Будем занулять все, кроме первого, элементы первой строки. С этой целью вычтем из второго, третьего и четвёртого столбцов первый столбец, умноженный соответственно на 2, 3 и 4. Получим
![]()
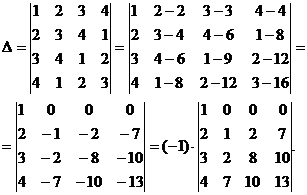
![]() Представленный в таком виде определитель разложим по первой строке:
Представленный в таком виде определитель разложим по первой строке:
![]()
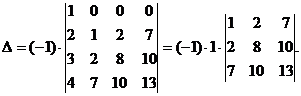
![]() Определитель третьего порядка, к которому свёлся исходный определитель, будем вычислять тем же способом. Вычтем из второго и третьего столбцов первый столбец, умноженный соответственно на 2 и 7. Получим (попутно вынося общие множители из столбцов)
Определитель третьего порядка, к которому свёлся исходный определитель, будем вычислять тем же способом. Вычтем из второго и третьего столбцов первый столбец, умноженный соответственно на 2 и 7. Получим (попутно вынося общие множители из столбцов)
![]()
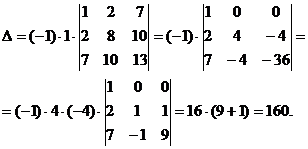
Выполните самостоятельно:
Вариант 1 №1. Вычислите определитель 2-го порядка:
№2. Вычислите определитель 3-го порядка:
№3. Вычислите определитель 4-го порядка:
| Вариант 2 №1. Вычислите определитель 2-го порядка:
№2. Вычислите определитель 3-го порядка:
№3. Вычислите определитель 4-го порядка:
|
Вариант 3 №1. Вычислите определитель 2-го порядка:
№2. Вычислите определитель 3-го порядка:
№3. Вычислите определитель 4-го порядка:
| Вариант 4 №1. Вычислите определитель 2-го порядка:
№2. Вычислите определитель 3-го порядка:
№3. Вычислите определитель 4-го порядка:
|
Итоги практического занятия.
Практическая работа №6
Тема: Решение систем линейных уравнений методом
Крамера. Контрольная работа.
Цель: приобретение базовых знаний в области фундаментальных разделов математики. Проверка усвоения знаний по применению определителей для решения систем линейных уравнений (СЛУ). Повторить и систематизировать знания по данной теме.
Задачи:
• развитие творческого профессионального мышления;
• познавательная мотивация;
• овладение языком науки, навыки оперирования понятиями;
• овладение умениями и навыками постановки и решения задач;
• углубление теоретической и практической подготовки;
• развитие инициативы и самостоятельности студентов.
1. Теоретические сведения:
1.1 Формулы Крамера.
СЛУ, в которых число уравнений равно числу неизвестных и определитель матрицы системы не равен 0, имеет единственное решение, которое определяется по формулам Крамера:
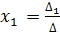 ;
;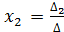 ;
;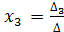 ;…;
;…;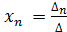 , где ∆- главный определитель системы, состоит из коэффициентов перед неизвестными,
, где ∆- главный определитель системы, состоит из коэффициентов перед неизвестными, ![]() ;
;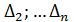 - вспомогательные определители системы, которые получают из главного путем замещения столбца перед
- вспомогательные определители системы, которые получают из главного путем замещения столбца перед ![]() ;
;![]() ;
;![]() соответственно на столбец свободных членов.
соответственно на столбец свободных членов.
Пример 1.
Решить систему уравнений 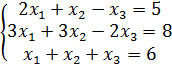
Решение. Вычислим главный определитель матрицы системы уравнений:
∆=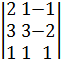 =2·3·1+1·(-2)·1+3·1·(-1)-1·3·(-1)-3·1·1-2·1·(-2)=5.
=2·3·1+1·(-2)·1+3·1·(-1)-1·3·(-1)-3·1·1-2·1·(-2)=5.
Следовательно, система имеет единственное решение, которое можно найти с помощью формул Крамера.
Вычислим вспомогательные определители системы:
![]() =
=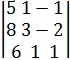 =15;
=15; ![]() =
=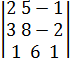 =5;
=5; ![]() =
=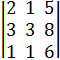 =10;
=10;
По формулам Крамера находим:
![]() =
=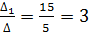 ;
;![]() =
=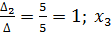 =
=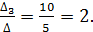
Ответ: (3;1;2)
2. Решите самостоятельно систему методом Крамера и методом:
Вариант 1 | Вариант 2 |
|
|
Вариант 3 | Вариант 4 |
|
|
Вариант 5 | Вариант 6 |
|
|
Вариант 7 | Вариант 8 |
|
|
Вариант 9 | Вариант 10 |
|
|
Подведение итогов практического занятия.
Практическая работа №7
Тема: Решение задач по теме «Множества». Формулы алгебры логики.
Цель: приобретение базовых знаний в области фундаментальных разделов математики. Повторить и систематизировать знания по данной теме.
Задачи:
• развитие творческого профессионального мышления;
• познавательная мотивация;
• овладение языком науки, навыки оперирования понятиями;
• овладение умениями и навыками постановки и решения задач;
• углубление теоретической и практической подготовки;
• развитие инициативы и самостоятельности студентов.
Теоретические сведения:
Элементы теории множеств
1. Логические символы
Квантор ![]() - заменяет выражение "для любого", "для произвольного", "для какого бы ни было".
- заменяет выражение "для любого", "для произвольного", "для какого бы ни было".
Квантор 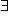 - заменяет выражение "существует", "найдется".
- заменяет выражение "существует", "найдется".
Запись ![]() (импликация) означает, что из справедливости высказывания A вытекает справедливость высказывания B. Если, кроме того, из справедливости высказывания B вытекает справедливость A, то записываем
(импликация) означает, что из справедливости высказывания A вытекает справедливость высказывания B. Если, кроме того, из справедливости высказывания B вытекает справедливость A, то записываем ![]() . Если
. Если ![]() , то высказывание B является необходимым и достаточным условием для того, чтобы выполнялось высказывание A.
, то высказывание B является необходимым и достаточным условием для того, чтобы выполнялось высказывание A.
Если предложения A и B справедливы одновременно, то записываем ![]() . Если же справедливо хотя бы одно из предложений A или B, то записываем
. Если же справедливо хотя бы одно из предложений A или B, то записываем ![]() .
.
2. Операции над множествами
Математическое понятие множества элементов принимается в качестве интуитивного. Множество задается правилом или признаком, согласно которому определяем, принадлежит ли данный элемент множеству или не принадлежит.
Множество обозначают символом A = {x}, где x - общее наименование элементов множества A. Часто множество записывают в виде A = {a, b, c, ...}, где в фигурных скобках указаны элементы множества A. Будем пользоваться обозначениями:
N - множество всех натуральных чисел;
Z - множество всех целых чисел;
Q - множество всех рациональных чисел;
R - множество всех действительных чисел;
C - множество всех комплексных чисел;
Z0 - множество всех неотрицательных целых чисел.
Запись ![]() означает, что элемент a принадлежит множеству A.
означает, что элемент a принадлежит множеству A.
Запись ![]() означает, что элемент a не принадлежит множеству A. Множество B, все элементы которого принадлежат множеству A, называется подмножеством множества A, и при этом записывают
означает, что элемент a не принадлежит множеству A. Множество B, все элементы которого принадлежат множеству A, называется подмножеством множества A, и при этом записывают ![]()
(см. рис. 1).
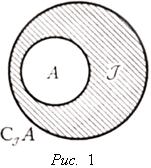
Всегда ![]() , так как каждый элемент множества, естественно, принадлежит A. Пустое множество, т. е. множество, не содержащее ни одного элемента, обозначим символом
, так как каждый элемент множества, естественно, принадлежит A. Пустое множество, т. е. множество, не содержащее ни одного элемента, обозначим символом ![]() . Любое множество содержит пустое множество в качестве своего подмножества.
. Любое множество содержит пустое множество в качестве своего подмножества.
Если 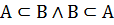 , то A и B называются равными множествами, при этом записывают A = B.
, то A и B называются равными множествами, при этом записывают A = B.
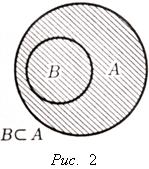
Если ![]() , то множество ℐ элементов множества А, не принадлежащих A, называется дополнением множества A к множеству (см. рис. 2).
, то множество ℐ элементов множества А, не принадлежащих A, называется дополнением множества A к множеству (см. рис. 2).
Дополнение множества A к множеству ℐ обозначают символом ![]() ; или просто CA, если известно, к какому множеству берется
; или просто CA, если известно, к какому множеству берется ![]()
![]() дополнение. Таким образом, С
дополнение. Таким образом, С![]() А=
А=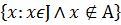
Если А⊂ℐ , то иногда дополнение множества B к множеству A называют разностью множеств A и B и обозначают A\B (см. рис. 3), т. е. 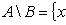
![]()
![]()
Пусть A и B - подмножества множества ℐ.

|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 |