Вариант 7
№1.
В группе 25 студентов, среди них 11 юношей. Найти вероятность того, что среди наудачу выбранных 6-ти студентов будут 3 девушки и 3 юноши.
№2.
Имеются 4 коробки с шарами.
1-я: 3 синих и 5 красных;
2-я: 5 синих и 6 красных;
3-я: 5 красных;
4-я: 10 синих.
Наудачу берут шар. Он красный. Найти вероятность того, что он из 2-й коробки.
№3
Двум студентам предложена задача. Вероятность того, что её решит 1-й студент равна 0,6, что решит 2-й – 0,85. Найти вероятность того, что задачу решат оба студента; что решит только один?
№4
Случайная величина X задана законом распределения:
| 1 | 2 | 3 |
| 0,1 | 0,4 | 0,5 |
Найти математическое ожидание М(X), дисперсию D(X) и среднее квадратичное отклонение σ(X).
Вариант 8
№1
Имеются 24 детали и среди них 18 стандартные. Случайным образом выбирают сразу 5. Какова вероятность, что среди выбранных ровно 4 стандартных?
№2
В цехе продукция производится на 3-х станках:
1-й станок 40% всей продукции, из них брак 1%;
2-й станок 45% всей продукции, из них брак 3%;
3-й станок 15% всей продукции, из них брак 2%.
Найти вероятность, что наудачу взятая деталь из всех произведенных стандартная. Какова вероятность, что она была произведена на 2-м станке?
№3
Процент всхожести семян равен 80%. Найти вероятность, что из посеянных 10 семян взойдут ровно 7?
№4
Случайная величина X задана законом распределения:
| 1 | 2 | 3 |
| 0,1 | 0,4 | 0,5 |
Найти математическое ожидание М(X), дисперсию D(X) и среднее квадратичное отклонение σ(X).
Вариант 9
№1
В урне лежат шары: 5 белых, 4 черных и 6 красных. Наудачу вынимают сразу два шара. Какова вероятность, что они окажутся одного цвета?
№2
Какова вероятность, что при десяти бросаниях игральной кости 5 очков выпадут ровно 3 раза?
№3
Цех производит продукцию на 2-х станках:
75% изготавливается на 1-м станке, среди них 10% составляют бракованные детали, остальные детали производятся на втором станке, среди них 5% бракованные. Какова вероятность, что наудачу взятая деталь окажется бракованной? Какая вероятность, что бракованная деталь произведена на 2-м станке?
№4
Случайная величина X задана законом распределения:
| 1 | 2 | 3 | 4 |
| 0,19 | 0,51 | 0,25 | 0,05 |
Найти математическое ожидание М(X), дисперсию D(X) и среднее квадратичное отклонение σ(X).
Вариант 10
№1
Три стрелка стреляют независимо друг от друга по цели. Вероятность попадания 1-м -0,85; 2-м – 0,7; 3-м – 0,9. Найти вероятность того, что будет:
1) хотя бы одно попадание;
2) ровно одно попадание;
если произведен один выстрел каждым.
№2
В магазин поступают часы, выпускаемые на 3-х заводах. Первый завод поставляет 30%, второй – 55%, третий – 15%. В продукции первого завод 12% часов спешат, второго завода – 35% часов спешат, третьего – 10% спешат. Найти вероятность того, что купленные часы спешат?
№3
Какова вероятность, что при десяти бросках игральной кости пять очков выпадут ровно 4 раза?
№4
Случайная величина X задана законом распределения:
| 1 | 2 | 3 | 4 |
| 0,15 | 0,5 | 0,25 | 0,1 |
Найти математическое ожидание М(X), дисперсию D(X) и среднее квадратичное отклонение σ(X).
Вариант 11
№1
Найти вероятность того, что при 10 бросках игральной кости, 5 очков выпадет ровно 6 раз?
№2
Детали на сборку попадают из трёх автоматов. Известно, что первый автомат дает 5% брака, второй – 6% брака, третий – 4% брака. Найти вероятность попадания на сборку бракованной детали, если 1-й автомат произвел 100 деталей, 2-й – 200 деталей и 3-й – 250 деталей. Какова вероятность, что бракованная деталь произведена на 1-м автомате?
№3
Из 4000 лотерейных билетов выигрышными являются 18. Какова вероятность, что из наудачу взятых 10 билетов хоть один будет с выигрышем?
№4
Случайная величина X задана законом распределения:
| -1 | 0 | 2 | 4 |
| 0,15 | 0,5 | 0,25 | 0,1 |
Найти математическое ожидание М(X), дисперсию D(X) и среднее квадратичное отклонение σ(X).
Вариант 12
№1
В белом ящике 10 красных и 5 синих шаров, в желтом ящике 12 красных и 14 синих шаров. Наудачу из некоторого ящика выбирают шар. Какая вероятность, что он красный? Какова вероятность, что красный шар вынут из белого ящика?
№2
По самолету противника производят три выстрела. Вероятность попадания при 1-м выстреле-0,6, при 2-м – 0,7, при 3-м – 0.8. Вероятность сбить самолет при условии попадания при 1-м выстреле – 0,3, при 2-м – 0,6 и при 3-м – 0,9. Найти вероятность того, что самолет будет сбит. Какова вероятность, что он будет сбит при 1-м выстреле?
№3
Два студента решают задачу независимо друг от друга. Вероятность того, что решит 1-й – 0,75, что решит 2-й – 0,85. Найти вероятность того, что:
а) решат оба;
б) решит только один?
№4
Случайная величина X задана законом распределения:
| -1 | 0 | 2 | 4 |
| 0,35 | 0,15 | 0,2 | 0,3 |
Найти математическое ожидание М(X), дисперсию D(X) и среднее квадратичное отклонение σ(X).
Вариант 13
№1.
В группе 22 студентов, среди них 10 юношей. Найти вероятность того, что среди наудачу выбранных 5-ти студентов будут 3 девушки и 2 юноши.
№2.
Имеются 4 коробки с шарами.
1-я: 7 синих и 6 красных;
2-я: 6 синих и 5 красных;
3-я: 4 красных;
4-я: 10 синих.
Наудачу берут шар. Он красный. Найти вероятность того, что он из 2-й коробки.
№3
Двум студентам предложена задача. Вероятность того, что её решит 1-й студент равна 0,6, что решит 2-й – 0,75. Найти вероятность того, что задачу решат оба студента; что решит только один?
№4
Случайная величина X задана законом распределения:
| -1 | 1 | 3 | 5 |
| 0,3 | 0,1 | 0,2 | 0,4 |
Найти математическое ожидание М(X), дисперсию D(X) и среднее квадратичное отклонение σ(X).
Вариант 14
№1
Имеются 25 детали и среди них 20 стандартные. Случайным образом выбирают сразу 5. Какова вероятность, что среди выбранных ровно 4стандартных?
№2
В цехе продукция производится на 3-х станках:
1-й станок 25% всей продукции, из них брак 5%;
2-й станок 45% всей продукции, из них брак 10%;
3-й станок 30% всей продукции, из них брак 2%.
Найти вероятность, что наудачу взятая деталь из всех произведенных на станке стандартная. Какова вероятность, что она была произведена на 3-м станке?
№3
Два стрелка независимо друг от друга производят выстрел по мишени. Вероятность попадания 1-м -
0,75, 2-м – 0,8. Какова вероятность, что после одного выстрела в мишени будет только одна пробоина?
№4
Случайная величина X задана законом распределения:
| -1 | 0 | 2 | 4 |
| 0,25 | 0,25 | 0,2 | 0,3 |
Найти математическое ожидание М(X), дисперсию D(X) и среднее квадратичное отклонение σ(X).
Вариант 15
№1
В урне лежат шары: 10 белых, 2 черных и 6 красных. Наудачу вынимают сразу два шара. Какова вероятность, что они окажутся одного цвета?
№2
В автоколонне 15 машин. Вероятность выхода на линию каждой машины – 0,9. Найти вероятность, что работа автоколонны будет осуществляться без сбоев, если для этого требуется, чтоб не менее 12 машин вышли на линию?
№3
Цех производит продукцию на 2-х станках:
75% изготавливается на 1-м станке, среди них 10% составляют бракованные детали, остальные детали производятся на втором станке, среди них 15% бракованные. Какова вероятность, что наудачу взятая деталь окажется бракованной? Какая вероятность, что бракованная деталь произведена на 2-м станке?
№4
Случайная величина X задана законом распределения:
| -1 | 0 | 2 | 4 |
| 0,35 | 0,15 | 0,2 | 0,3 |
Найти математическое ожидание М(X), дисперсию D(X) и среднее квадратичное отклонение σ(X).
Вариант 16
№1
Три стрелка стреляют независимо друг от друга по цели. Вероятность попадания 1-м -0,7; 2-м – 0,65; 3-м – 0,8. Найти вероятность того, что будет:
1) хотя бы одно попадание;
2) ровно одно попадание;
если произведен один выстрел каждым.
№2
В магазин поступают часы, выпускаемые на 3-х заводах. Первый завод поставляет 50%, второй – 35%, третий – 15%. В продукции первого завод 20% часов спешат, второго завода – 30% часов спешат, третьего – 10% спешат. Найти вероятность того, что купленные часы спешат?
№3
Какова вероятность, что при десяти бросках игральной кости пять очков выпадут ровно 6 раз?
№4
Случайная величина X задана законом распределения:
| -1 | 0 | 2 | 4 |
| 0,5 | 0,1 | 0,2 | 0,2 |
Найти математическое ожидание М(X), дисперсию D(X) и среднее квадратичное отклонение σ(X).
Вариант 17
№1
В мастерской работают 5 моторов. Для каждого мотора вероятность перегрева к обеденному перерыву равна 0,8. Найти вероятность того, что к обеденному перерыву перегреются:
1) ровно 3 мотора;
2) перегреются все моторы?
№2
Детали на сборку попадают из трёх автоматов. Известно, что первый автомат дает 3% брака, второй – 2% брака, третий – 4% брака. Найти вероятность попадания на сборку бракованной детали, если 1-й автомат произвел 1500 деталей, 2-й – 1000 деталей и 3-й – 2000 деталей. Какова вероятность, что бракованная деталь произведена на 2-м станке?
№3
Найти вероятность того, что при 10 бросках игральной кости, 5 очков выпадет ровно 7 раз?
№4
Случайная величина X задана законом распределения:
| 1 | 2 | 3 | 4 |
| 0,5 | 0,1 | 0,2 | 0,2 |
Найти математическое ожидание М(X), дисперсию D(X) и среднее квадратичное отклонение σ(X).
Вариант 18
№1
В белом ящике 13 красных и 7 синих шаров, в желтом ящике 12 красных и 14 синих шаров. Наудачу из некоторого ящика выбирают шар. Какая вероятность, что он красный? Какова вероятность, что красный шар вынут из белого ящика?
№2
По самолету противника производят три выстрела. Вероятность попадания при 1-м выстреле-0,4, при 2-м – 0,7, при 3-м – 0.75. Вероятность сбить самолет при условии попадания при 1-м выстреле – 0,3, при 2-м – 0,6 и при 3-м – 0,9. Найти вероятность того, что самолет будет сбит. Какова вероятность, что он будет сбит при 1-м выстреле?
№3
Два студента решают задачу независимо друг от друга. Вероятность того, что решит 1-й – 0,5, что решит 2-й – 0,9. Найти вероятность того, что:
а) решат оба;
б) решит только один?
№4
Случайная величина X задана законом распределения:
| -1 | 0 | 2 | 4 |
| 0,4 | 0,1 | 0,3 | 0,2 |
Найти математическое ожидание М(X), дисперсию D(X) и среднее квадратичное отклонение σ(X).
Практическая работа № 11,часа)
Тема: Тригонометрическая форма комплексного числа.
Цель: Проверить на практике знание понятия комплексного числа, умение находить модуль и аргумент комплексного числа, умение переходить от одной формы записи к другой и выполнять действия с комплексными числами в различных формах.
Теоретический материал: Алгебраическая форма комплексного числа
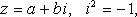 где a=Rez- действительная часть z, b=Imz– мнимая часть z.
где a=Rez- действительная часть z, b=Imz– мнимая часть z.
Так выполняются действия с комплексными числами в алгебраической форме:

![]()
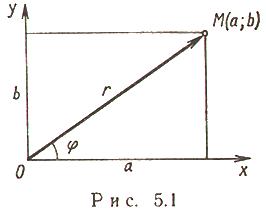
Тригонометрическая форма комплексных чисел (рис. 5.1)
![]() где r - модуль;φ - агрумент комплексного числа.
где r - модуль;φ - агрумент комплексного числа.
r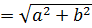 , tgφ=
, tgφ= ;
; 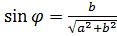 ;
;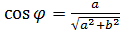 .
.
Если
![]()
1) При умножении комплексных чисел в тригонометрической форме их модули перемножаются, а аргументы складываются:
z1 z2 = r1r2 (cos (φ1 + φ2) + i sin (φ1 + φ
2) При делении комплексных чисел в тригонометрической форме их модули делятся, а аргументы вычитаются:
![]() =
=![]() (cos (φ1 - φ2) + i sin (φ1 - φ
(cos (φ1 - φ2) + i sin (φ1 - φ
1) Формула Муавра
![]() =
=![]() (cos nφ + i sin nφ) (3)
(cos nφ + i sin nφ) (3)
2) Извлечение корней из комплексных чисел:
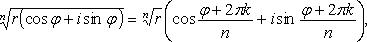
![]()
Показательная (экспоненциальная) форма комплексных чисел
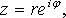 где r - модуль; φ - аргумент;
где r - модуль; φ - аргумент;
![]() =
=![]() +i
+i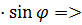 z=r(
z=r(![]() +i
+i![]() )
)
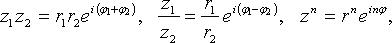
![]() =
=![]() ·
·![]() , где κ=0,1,…n-1.
, где κ=0,1,…n-1.
Выполните самостоятельно:
Вариант 1 Дано:
Записать каждое число в двух других формах и выполнить действия: 1) 2) 3) | Вариант 2 Дано:
Записать каждое число в двух других формах и выполнить действия: 1) 2) 3) |
Вариант 3 Дано:
Записать каждое число в двух других формах и выполнить действия: 4) 5) 6) | Вариант 4 Дано:
Записать каждое число в двух других формах и выполнить действия: 4) 5) 6) |
Вариант 5 Дано:
Записать каждое число в двух других формах и выполнить действия: 7) 8) 9) | Вариант 6 Дано:
Записать каждое число в двух других формах и выполнить действия: 7) 8) 9) |
Подведение итогов практической работы.
ЛИТЕРАТУРА:
1. Григорьев высшей математики-М.: «Академия», 2013.-320с.
2. Богомолов занятия по математике-М.: Высш. шк.,2003.-495 с.
3. Омельченко -Ростов-на-Дону: Феникс, 2012.-380с.
4. http://*****/elena-parkhomenko

|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 |




