Информационная безопасность и защита информации (стр. 6 )

При достаточной длине блока, в пределах которого осуществляется перестановка, и сложном неповторяющемся порядке перестановки можно достигнуть приемлемой для простых практических приложений стойкости шифра.

Метод простой перетановки

При шифровании методом простой перестановки производят деление открытого текста на блоки одинаковой длины, равной длине ключа. Ключ длины n представляет собой последовательность неповторяющихся чисел от 1 до n. Символы открытого текста внутри каждого из блоков переставляют в соответствие с символами ключа. Элемент ключа Ki в заданной позиции блока говорит о том, что на данное место будет помещен символ открытого текста с номером Ki из соответствующего блока.

Пример 4.5.

Зашифруем открытый текст «ПРИЕЗЖАЮДНЕМ» методом перестановки с ключом К=3142.

Для дешифрования шифротекста необходимо символы шифротекста перемещать в позицию, указанную соответствующим им символом ключа Ki.

Алгорита Гамильтона

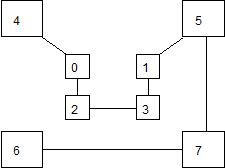
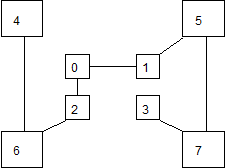
Весьма высокую стойкость шифрования можно обеспечить усложнением перестановок по маршрутам типа гамильтоновских . При этом, для записи символов шифруемого текста используются вершины некоторого гиперкуба, а знаки зашифрованного текста считываются по маршрутам Гамильтона, причем используется восемь различных маршрутов. Размер ключа перестановки в данном случае равен восьми по числу вершин куба. Для примера, два из маршрутов Гамильтона представлено на рис. 4.2. Первому маршруту соответствует перестановка -7-6, второму -7-3 (нумерация символов в блоке осуществляется с нуля).

Рис. 4.2. Пример маршрутов Гамильтона

Пример 4.6.

Зашифруем открытый текст «ВОСЕМЬ МАРШРУТОВ» с помощью перестановок Гамильтона при использовании в качестве ключа двух перестановок, представленных на рис. 4.2.

4.2.3.  Шифрование методом гаммирования

Под гаммированием понимают наложение на открытые данные по определенному закону гаммы шифра [2].

Гамма шифра – псевдослучайная последовательность, вырабатываемая по определенному алгоритму, используемая для шифровки открытых данных и дешифровки шифротекста.

Общая схема шифрования методом гаммирования представлена на рис. 4.3.

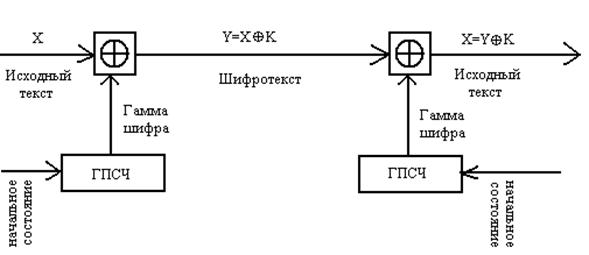
Рис. 4.3. Схема шифрования методом гаммирования

Принцип шифрования заключается в формировании генератором псевдослучайных чисел (ГПСЧ) гаммы шифра и наложении этой гаммы на открытые данные обратимым образом, например, путем сложения по модулю два. Процесс дешифрования данных сводится к повторной генерации гаммы шифра и наложении гаммы на зашифрованные данные. Ключом шифрования в данном случае является начальное состояние генератора псевдослучайных чисел. При одном и том же начальном состоянии ГПСЧ будет формировать одни и те же псевдослучайные последовательности.

Перед шифрованием открытые данные обычно разбивают на блоки одинаковой длины, например по 64 бита. Гамма шифра также вырабатывается в виде последовательности блоков той же длины.

Стойкость шифрования методом гаммирования определяется главным образом свойствами гаммы – длиной периода и равномерностью статистических характеристик. Последнее свойство обеспечивает отсутствие закономерностей в появлении различных символов в пределах периода. Полученный зашифрованный текст является достаточно трудным для раскрытия. По сути дела гамма шифра должна изменяться случайным образом для каждого шифруемого блока.

Обычно разделяют две разновидности гаммирования – с конечной и бесконечной гаммами. При хороших статистических свойствах гаммы стойкость шифрования определяется только длиной периода гаммы. При этом, если длина периода гаммы превышает длину шифруемого текста, то такой шифр теоретически является абсолютно стойким, т. е. его нельзя вскрыть при помощи статистической обработки зашифрованного текста, а можно раскрыть только прямым перебором. Криптостойкость в этом случае определяется размером ключа.

  4.3.Элементы криптоанализа

Любая попытка со стороны злоумышленника расшифровать шифротекст C и получить открытый текст М не имея подлинного ключа, называется криптоаналитической атакой.

Криптоанализ — наука о методах получения исходного значения зашифрованной информации, не имея доступа к секретной информации (ключу), необходимой для этого. В большинстве случаев под этим подразумевается нахождение ключа. Проще говоря, криптоанализ — это взламывание кода, хотя этот термин имеет и строго технические значение.

Под термином «криптоанализ» также понимается попытка найти уязвимость в криптографическом алгоритме или протоколе. Хотя основная цель осталась неизменной с течением времени, методы криптоанализа претерпели значительные изменения, эволюционировав от использовния лишь ручки и бумаги до широкого применения вычислительных мощностей компьютеров в наши дни. Если раньше криптоаналитиками были большей частью лингвисты, то в наше время это удел «чистых» математиков.

Один из широко используемых методов криптоанализа для недостаточно криптостойких алгоритмов заключается в анализе частотности символов, встречающихся в зашифрованном тексте.

Особенностью большинства искусственных языков (и всех естественных) является то, что они имеют характерное частотное распределение букв и других знаков.

При этом многие, недостаточно стойкие простейшие алгоритмы шифрования сохраняют частотность символов в тексте. В основном этот недостаток свойственен простейшим методам замены (например, шифру Цезаря и ему подобным). Это распределение частотности дает криптоаналитику путь к раскрытию шифра.

Частотное распределение букв русского и английского алфавита в художественных текстах представлено ниже

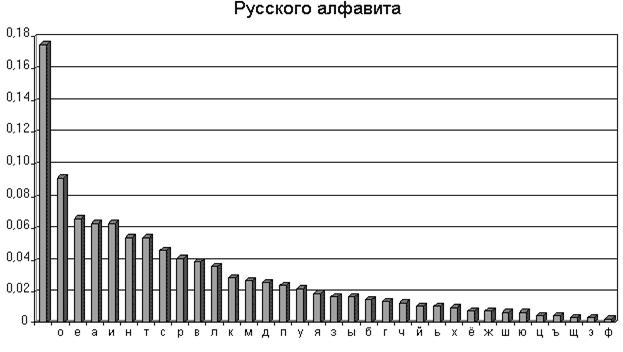
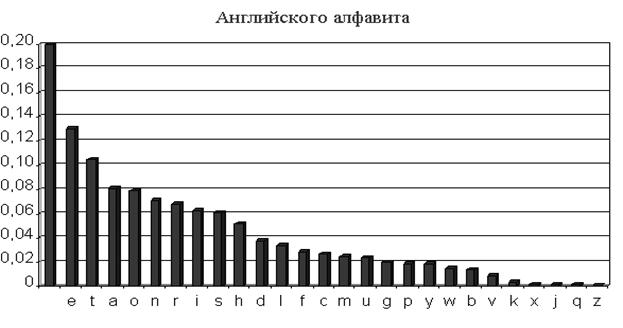
Исследовав шифротекст и обнаружив, что наиболее часто встречаемый в нем символ – это «Б», а второй по встречаемости - «К», криптоаналитик может сделать вывод, что символ «Б» это «Пробел», а «К» это буква «о».

Таким образом, путем анализа частотности символов шифротекста и сравнения их с частотностями букв русского (английского) текста можно составить таблицу замен и дешифровать шифротекст.

При вскрытии шифротекста необходимо иметь в виду, что отдельные буквы имеют примерно одинаковую частоту встречаемости в текстах. Например, буквы «а» и «е», «р» и «в», «л» и «с». Для таких букв сформированные замены могут оказаться неверными. В этом случае, необходим интеллектуальный эвристический анализ человеком полученного в результате дешифровки текста. Цель эвристического анализа – выявить те замены, которые оказались неверными (по смыслу текста), и сформировать верные замены.

Принимая во внимание выше приведенный факт, следует отметить, что дешифровка путем составления таблицы замен сразу всех символов закрытого текста может вызвать проблемы. Как правило, производят дешифровку первых 15-20 наиболее часто встречаемых в шифротексте символов, далее делают интеллектуальные подмены, далее остальные символы дешифруют по смыслу теста (принимая во внимание их частотности).

  4.4. Современные симметричные системы шифрования

При построении стойких шифров необходимо использовать два основных принципа – рассеивание и перемешивание [2].

Рассеивание предполагает распространение влияния одного знака открытого текста на множество знаков шифротекста, что позволяет скрыть статистические свойства открытого текста.

Перемешивание предполагает использование таких шифрующих преобразований, которые усложняют восстановление взаимосвязи статистических свойств открытого текста и шифротекста.

Обычно для достижения эффектов рассеивания и перемешивания используют шифры, реализованные в виде последовательности простых традиционных шифров, каждый из которых вносит свой вклад в суммарное рассеивание и перемешивание. Наиболее часто при этом используют традиционные шифры перестановки и замены.

При многократном чередовании простых перестановок и замен, управляемых достаточно длинным секретным ключом, можно получить очень стойкий шифр с хорошим рассеиванием и перемешиванием. Большинство существующих стандартов шифрования построены в полном соответствии с данной методологией.

Алгоритм, изложенный в стандарте DES (Data Encryption Standard), широко применялся до 2002 года для шифрования данных в США [11]. Он был разработан фирмой IBM для собственных целей, но после был рекомендован к применению в качестве федерального стандарта шифрования. Алгоритм DES не является закрытым и был опубликован для широкого ознакомления. Алгоритм предназначен для шифровки и расшифровки блоков данных длиной по 64 бита под управлением 64-битового ключа, в котором значащими являются 56 бит. Дешифрование в DES выполняется путем повторения операций шифрования в обратной последовательности.

Обобщенная схема шифрования алгоритма DES представлена на рис. 4.4

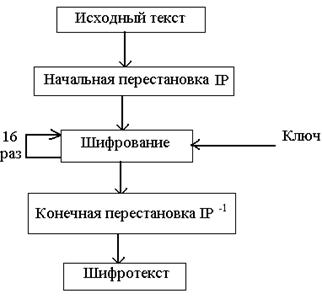
Рис. 4.4. Обобщенная схема шифрования алгоритма DES

Число различных ключей DES-алгоритма равно 256 = 7*1016 . Недавние исследования показали, что современная технология позволяет создать вычислительное устройство стоимостью около 1 млн. долларов, способное вскрыть секретный ключ с помощью полного перебора в среднем за 3,5 часа.

В настоящее время криптостойкость алгоритма DES не удовлетворяет реальным потребностям, в связи с чем, данный алгоритм в настоящее время заменен в США на более стойкий алгоритм AES.

Российская Федерация имеет свой собственный стандарт симметричного шифрования. Этот стандарт закреплен ГОСТом №, принятом в 1989 году в СССР [12]. Данный стандарт обязателен для организаций, предприятий и учреждений, применяющих криптографическую защиту данных, относящихся к государственной тайне, хранимых и передаваемых в сетях ЭВМ и в отдельных вычислительных комплексах. Помимо нескольких тесно связанных между собой процедур шифрования, в стандарте описан алгоритм выработки имитовставки.

Имитовставка есть криптографическая контрольная комбинация, то есть код, вырабатываемый из исходных данных с использованием секретного ключа с целью имитозащиты, т. е. защиты данных от внесения в них несанкционированных изменений.

Алгоритм предусматривает четыре режима работы:

-  шифрование данных в режиме простой замены;

-  шифрование данных в режиме гаммирования;

-  шифрование данных в режиме гаммирования с обратной связью;

-  выработка имитовставки.

В ГОСТе ключевая информация состоит из двух структур данных - собственно ключа, необходимого для всех шифров, и таблицы замен. Ключ является массивом из восьми 32-битных элементов кода (всего 256 бит).

Имитовставка добавляется к зашифрованным данным для обеспечения их имитозащиты.

Рассмотрим вопрос качества ключевой информации и источников ключей. Ключ должен являться массивом статистически независимых битов, принимающих с равной вероятностью значения 0 и 1. Ключи, выработанные с помощью некоторого датчика истинно случайных чисел, будут качественными с вероятностью, отличающейся от единицы на ничтожно малую величину.

Если же ключи вырабатываются с помощью генератора псевдослучайных чисел, то для отбраковки ключей с плохими статистическими характеристиками могут быть использованы различные статистические критерии. На практике обычно хватает двух критериев – для проверки равновероятного распределения битов ключа между значениями 0 и 1 обычно используется критерий «хи квадрат», а для проверки независимости битов ключа – критерий серий.

  4.5. Асимметричные криптосистемы

4.5.1. Принципы асимметричного шифрования

Наряду с вычислительной простотой и интуитивной понятностью симметричных криптосистем, они обладают рядом серьезных недостатков. К основным недостаткам симметричных криптосистем относят проблему распространения симметричных ключей и проблему их хранения [2].

При использовании симметричных криптосистем для шифрования информации между пользователями криптографической сети необходимо обеспечить безопасную передачу ключей шифрования между всеми доверенными пользователями (участниками криптографического обмена). При этом передача ключа шифрования обязательно должна осуществляться по закрытому каналу, так как перехват злоумышленником данного ключа ведет к компрометации всей криптографической сети.

В связи с этим, использование симметричных алгоритмов предполагает наличие взаимного доверия сторон. Вероятность компрометации ключей тем выше, чем большее количество пользователей входит в криптографическую сеть. Это является большим недостатком симметричных криптосистем.

В отличие от симметричных криптосистем, асимметричные криптосистемы используют различные ключи для шифрования и дешифрования сообщений.

Ключи в асимметричных криптосистемах всегда генерируются парами и состоят из двух частей – открытого ключа (ОК) и секретного ключа (СК).

Открытый ключ используется для шифрования информации, является доступным для всех пользователей и может быть опубликован в общедоступном месте для использования всеми пользователями криптографической сети. Дешифрование информации с помощью открытого ключа невозможно.

Секретный ключ является закрытым и не может быть восстановлен злоумышленником из открытого ключа. Этот ключ используется для дешифрования информации и хранится только у одного пользователя – сгенерировавшего ключевую пару.

Функциональная схема взаимодействия участников асимметричного криптографического обмена представлена на рис. 4.5.

В данной схеме участвует получатель секретного сообщения А и отправитель секретного сообщения B. ОКА – открытый ключ пользователя А, СКА – секретный ключ пользователя А. Ключевая пара (ОКА, СКА) сгенерирована на стороне получателя А, после чего открытый ключ данной пары ОКА отправляется по открытому каналу пользователю B. Предполагается, что злоумышленнику также известен открытый ключ ОКА.

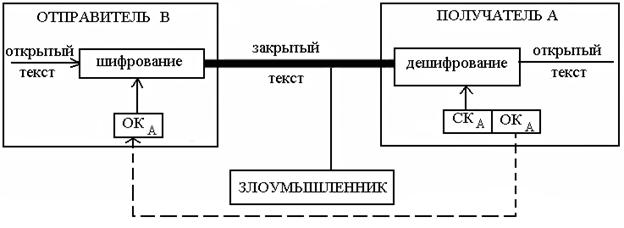
Рис. 4.5. Функциональная схема асимметричной криптосистемы

Отправитель B, зная открытый ключ получателя А, может зашифровать на данном ключе открытый текст и переслать его пользователю А. Пользователь А с помощью своего секретного ключа, соответствующего ОКА, может дешифровать присланное пользователем B сообщение. Злоумышленник, зная ОКА и закрытый текст, не может получить доступ не к СКА, не к открытому тексту.

Рис 4.5 отражает только одностороннюю схему взаимодействия в рамках асимметричных криптосистем. Для реализации двустороннего обмена необходима реализация следующих шагов:

1. Пользователь A генерирует ключевую пару (ОКА, СКА).

2. Пользователь B генерирует ключевую пару (ОКB, СКB).

3. Пользователи A и B должны обменяться своими открытыми ключами. Пользователь А передает свой открытый ключ ОКА пользователю B, пользователь B передает свой открытый ключ ОКB пользователю A.

4. Пользователь А шифрует информацию для пользователя B на ключе ОКB, пользователь B шифрует информацию для пользователя A на ключе ОКA.

5. Пользователь А дешифрует информацию, присланную ему от пользователя B, на ключе СКА, пользователь B дешифрует информацию, присланную ему от пользователя A, на ключе СКB.

Обмен открытыми ключами в современных криптографических сетях, насчитывающих десятки и даже сотни тысяч пользователей более удобно реализовывать, используя специально выделенные для этого центры распределения ключей. Пользователь A может выложить на центр распределения ключей свой открытый ключ и любой другой пользователь, желающий шифровать информацию для A, может обратиться в данный центр и забрать его открытый ключ. Схема распределения ключей в данном случае может выглядеть следующим образом (рис. 4.6).

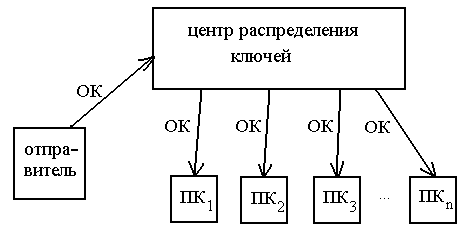
Рис. 4.6. Схема распределения ОК с использованием центра распределения ключей

В настоящее время все более распространенным подходом к распределению ключей становится подход, основанный на реализации инфраструктуры открытых ключей PKI и удостоверяющих центров (УЦ).

У. Диффи и М. Хеллман сформулировали требования, выполнение которых обеспечивает безопасность асимметричной криптосистемы [13]:

1. Вычисление ключевой пары (ОК, СК) должно быть достаточно простым.

2. Отправитель, зная открытый ключ получателя, может легко получить шифротекст.

3. Получатель, используя свой секретный ключ, может легко из шифротекста восстановить исходное сообщение.

4. Знание открытого ключа злоумышленником не должно влиять на криптостойкость системы. При попытке вычислить злоумышленником закрытый ключ по открытому, он должен наталкиваться на непреодолимую вычислительную проблему.

5. Злоумышленник, зная шифротекст и открытый ключ, на котором осуществлялось шифрование, при попытке восстановить исходный текст должен наталкиваться на непреодолимую вычислительную проблему.

4.5.2. Однонаправленные функции

Реализация асимметричных криптосистем основана на использовании однонаправленных функций.

Пусть X и Y – некоторые произвольные множества. Функция 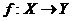называется однонаправленной функцией, если для любого элемента можно легко вычислить его образ , однако, зная элемент , достаточно сложно получить его прообраз 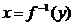, хотя такой элемент x однозначно существует, хотя бы один.

Одним из основных критериев, по которому функцию f можно считать однонаправленной, является отсутствие эффективных алгоритмов обратного преобразования , что не позволяет обратить данную функцию за приемлемое время.

Рассмотрим несколько примеров однонаправленных функций, имеющих большое значение для криптографии.

Целочисленное умножение

Вычисление произведения двух очень больших целых чисел P и Q (N=P*Q) является несложной задачей для ЭВМ. Однако, решение обратной задачи, заключающейся в нахождении делителей P и Q большого числа N (в особенности, когда P и Q – большие простые числа), является практически неразрешимой задачей. Если N»264 и P»Q, то задача факторизации не разрешима за приемлемое время на современных ЭВМ. Поэтому целочисленное умножение является однонаправленной функцией.

Модульная экспонента

Возведение очень большого числа A в очень большую степень x по любому модулю M (), то есть вычисление является несложной задачей для ЭВМ. Однако решение обратной задачи – нахождения степени x по известным у,A,M такой, что (задача дискретного логарифмирования, ), практически не разрешима за приемлемое время на современных ЭВМ (эффективного алгоритма вычисления дискретного логарифма пока не найдено). Поэтому модульная экспонента является однонаправленной функцией. Рассмотрим простую интерпретацию сказанного. Пусть А=2, х=2, М=4. Тогда = 0. Пусть А=2, х=3, М=4. Тогда = 0. Отсюда видно, что по у вычислить х можно только полным перебором всех вариантов даже, если известны А и М.

Кроме однонаправленных функций важное значение для криптографии с открытым ключом имеют однонаправленные функции с «потайным входом», эффективное обращение которых возможно, если известен секретный «потайной ход» (секретное число или другая информация, ассоциируемая с функцией).

4.5.3. Алгоритм шифрования RSA

Алгоритм RSA был предложен в 1978 году Р. Райвестом, А. Шамиром, А. Адлеманом и был назван по первым буквам фамилий его авторов. Данный алгоритм стал первым алгоритмом шифрования с открытым ключом. Надежность данного алгоритма основывается на трудности факторизации больших чисел и вычисления дискретных логарифмов [14,2].

В криптосистеме RSA открытый ключ ОК, секретный ключ СК, исходное сообщение М и шифротекст С являются целыми числами от 0 до N-1, где N – модуль.

Пусть пользователь А является получателем сообщения, которое ему должен переслать отправитель B.

Пользователь A должен вначале сгенерировать ключевую пару RSA, это он делает следующим образом.

Алгоритм формирования ключевой пары пользователем А

1. Выбираем случайные большие простые числа P и Q. Для обеспечения максимальной безопасности P и Q выбирают примерно равной длины и хранят в секрете.

2. Вычисляем модуль 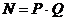. Формируем функцию Эйлера .

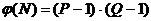3. Открытый ключ ОКА выбирается случайно таким образом, чтобы выполнялись следующие условия:

4. Секретный ключ СКA находится по сформированному открытому ключу так, что

Пользователь A может легко найти СКА, используя расширенный алгоритм Евклида, зная числа P и Q, а значит и .

Любой другой пользователь не может, зная открытый ключ ОКА вычислить СКА, так как ему не известны числа P и Q. Для их нахождения ему потребуется факторизовать известное ему число N, что является вычислительно сложной задачей.

Шифрование и дешифрование сообщений в криптосистеме RSA

Для того, чтобы зашифровать открытое сообщение M, отправитель B должен возвести его в степень открытого ключа пользователя А по модулю N. То есть шифрование выполняется в соответствие с формулой

Обращение данной функции, то есть определение значения M по известным значениям С, ОКА, N практически не осуществимо при больших N ().

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16