Лабораторные работы и задачи по физической химии (стр. 8 )

6.  Измерить рН приготовленных буферных растворов.

7.  Измерить рН контрольного раствора.

8.  Полученные данные показать преподавателю и занести в таблицу.

9.  Выключить прибор. Опустить стеклянный электрод и наконечник электролитического мостика (или хлоридсеребряный электрод при другой конструкции прибора) в стакан с дистиллированной водой.

10.Рассчитать активности водородных ионов во всех растворах и результаты занести в таблицу.

11.Привести в порядок рабочее место и сдать его дежурному.

12.Сформулировать выводы.

Работа 4.2

Потенциометрическое определение буферной ёмкости

Цель работы: определение величины буферной ёмкости буферного раствора.

Целевые задачи: закрепление навыка работы на рН-метре и определения достоверности его показаний; умение определять буферную ёмкость растворов по кислоте и щёлочи графическим способом.

Значение рН буферного раствора зависит от соотношения концентраций компонентов буферной смеси, находящихся в химическом равновесии. Оно мало меняется при концентрировании и разбавлении раствора, а также при введении относительно небольших количеств веществ, в том числе кислот и оснований, взаимодействующих с одним из компонентов буферного раствора. Количественно буферное действие характеризуется буферной ёмкостью. Ёмкость буферного раствора соответствует числу эквивалентов (или миллиэквивалентов) сильной кислоты или сильного основания, которое необходимо добавить к 1 л раствора, чтобы изменить его рН на единицу. Буферная ёмкость возрастает при увеличении начальных концентраций его компонентов и максимальна при их равенстве. Наибольшей буферной ёмкостью обладает раствор, в котором отношение количеств кислоты и сопряжённого основания равно единице.

Оснащение рабочего места

рН-метр Эталонные буферные растворы

Стакан на 50 мл Растворы HCl и NaOH (0,1 н.)

Бюретки на 25 мл Растворы реактивов для приготовления

Магнитная мешалка буферных растворов

Проведение опыта

1.   Проверить оснащение рабочего места.

2.   Включить рН-метр и дать ему прогреться не менее 20 минут.

3.   Приготовить два одинаковых образца по 20 мл буферного раствора, указанного преподавателем.

4.   Проверить правильность работы рН-метра, измерив рН эталонных буферных растворов.

5.   Стакан с 20 мл исследуемого буферного раствора и опущенным в него магнитным стержнем поставить на столик магнитной мешалки. Погрузить в раствор стеклянный электрод и наконечник электролитического мостика (или хлоридсеребряный электрод при другой конструкции прибора). Подвести к стакану бюретку с 0,1н. раствором NaОН.

6.   Включить магнитную мешалку. Измерить рН раствора.

7.   Не снимая стакана со столика магнитной мешалки и не прекращая перемешивания прилить к буферному раствору из бюретки 1 мл раствора NaОН. После этого вновь измерить рН раствора.

8.   Продолжать приливать из бюретки раствор NaОН порциями по 1 мл, каждый раз измеряя и записывая в таблицу величины рН, до тех пор, пока рН изменится больше, чем на единицу по сравнению с исходным значением.

9.   Произвести согласно п. п. 7 – 8 аналогичные измерения с другой порцией исходного буферного раствора, добавляя к нему 0,1н. раствор HCl.

10. После проверки экспериментальных данных у преподавателя занести их в таблицу. Выключить рН-метр и магнитную мешалку. Погрузить стеклянный электрод и наконечник электролитического мостика в дистиллированную воду.

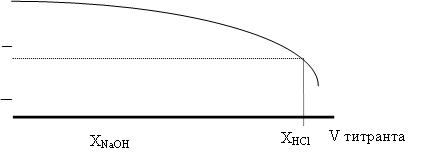
11. Построить графики зависимости рН раствора от объёма прибавленных растворов основания и кислоты. Определить по графику точные объёмы (мл) растворов титрантов (ХNaOH и XHCl), необходимые для изменения рН раствора на единицу.

рН

12. Рассчитать буферную ёмкость В раствора по NaOH и по HCl по уравнениям:

где С - концентрация титранта, моль/л; V - объём (мл) исходного буферного раствора, взятый для опыта. Размерность буферной ёмкости при вычислениях по этой формуле - ммоль-экв/л.

13. Привести в порядок рабочее место и сдать его дежурному.

14. Сформулировать выводы.

Тема 5. Кинетика химических реакций

Химическая кинетика занимается изучением скорости химических реакций, в том числе влияния на неё различных факторов (температуры, давления, концентрации, присутствия катализаторов и др.), а также их механизма. Отсюда следует её первостепенное значение для определения и продления сроков годности лекарственных препаратов, расчета эффективности аппаратов, используемых для получения лекарственных веществ, для изучения механизма как химических, так и биохимических реакций. Такие составляющие действия лекарств, как высвобождение, всасывание из пищеварительного тракта и через кожу, диффузия через клеточные мембраны, взаимодействие с рецептором и т. п. описываются кинетическими уравнениями; их изучением занимаются специальные фармакологические дисциплины - фармакокинетика и фармакодинамика.

Присутствие катализаторов сказывается не только на процессах получения, но и на реакциях разложения веществ, в том числе лекарственных. При этом различные примеси, в том числе продукты разложения, материал сосуда или упаковки могут являться как катализаторами, так и ингибиторами. Ингибиторы в ряде случаев специально вводятся в лекарственные препараты для продления сроков годности.

Практически все реакции, протекающие в живом организме, осуществляются с помощью биологических катализаторов - ферментов (энзимов). На основе ферментов создано много лекарственных препаратов, применяемых главным образом для стимуляции обменных процессов.

Изучив данную тему и выполнив лабораторные работы, относящиеся к ней, студент должен знать:

·  виды скорости химических реакций, факторы, влияющие на неё;

·  закон действующих масс;

·  кинетическую классификацию химических реакций;

·  понятие о молекулярности и порядке (псевдопорядке) реакций;

·  методы определения порядка реакций;

·  кинетические уравнения реакций 1 и 2 порядков;

·  способы расчета сроков годности и времени полупревращения веществ в реакциях 1 и 2 порядков;

·  правило Вант-Гоффа;

·  понятие о температурном коэффициенте скорости;

·  уравнение Аррениуса, его практическое значение для расчета сроков годности лекарственных веществ методом ускоренного старения.

Студент должен уметь:

· определять скорость химических реакций;

· определять порядок реакции;

· рассчитывать константы скорости реакции 1 и 2 порядка;

· рассчитывать энергию активации реакции;

· рассчитывать сроки годности лекарственных веществ.

Студент должен приобрести или закрепить навыки:

· титрования растворов;

· работы с поляриметром;

· работы с фотоколориметром;

· пользования мерной посудой и лабораторным оборудованием;

· расчетов по различным уравнениям;

· построения графиков и интерпретации экспериментальных и расчет - ных данных;

· пользования справочной литературой.

Любая химическая реакция представляет собой совокупность элементарных актов химического превращения, каждый из которых есть превращение одной или нескольких частиц реагентов в частицы продуктов. Простые реакции состоят из однотипных элементарных актов. В зависимости от числа частиц, принимающих участие в элементарном акте, они подразделяются на моно-, би-, и тримолекулярные реакции. Сложные реакции осуществляются при протекании разнотипных элементарных актов.

Согласно закону действующих масс скорость v простых реакций прямо пропорциональна произведению концентраций исходных веществ, возведенных в степени (как правило, совпадающие со стехиометрическими коэффициентами в уравнении реакции). Так, для реакции вида:

aA + bB ® yY + xX

скорость можно рассчитать по уравнению v = k CAa CBb,

где k - константа скорости реакции, представляющая собой скорость её при концентрациях реагентов, равных 1 при той же температуре, т. е. скорость реакции в стандартных условиях.

Показатели степени при концентрациях определяют порядок реакции по данному веществу, а их сумма - общий (суммарный) порядок реакции.

Порядок реакции может изменяться в зависимости от условий. Главным образом на него влияет соотношение концентраций реагентов. Поэтому порядок нельзя предсказать априорно, только по виду уравнения реакции. В каждом конкретном случае порядок реакции должен определяться экспериментально.

Для определения порядка существуют различные методы, из которых наиболее часто употребляются следующие:

1.   Метод подстановки. По экспериментальным данным для различных отрезков времени рассчитывается несколько значений константы скорости по кинетическим уравнениям 1, 2, 3 порядков. Если близкие друг другу значения получаются при использовании уравнений 1 порядка, то принимается, что реакция имеет порядок 1. Если же при использовании определенного уравнения получаются различные по величине значения k, то нужно провести расчет по уравнениям для других порядков. В том случае, когда ни одно из уравнений не позволяет получить близкие значения k, принимается, что реакция имеет дробный порядок и сложный механизм.

2.   Графический метод. Подбирается вид уравнения, при котором график зависимости концентрации реагентов от времени представляет собой прямую линию. Для первого порядка это уравнение lgC - t, для второго 1/C - t и т. д.

3.  Метод времени полупревращения. Для характеристики протекания реакции во времени, кроме скорости и константы скорости, используют и другие величины, например, время полупревращения t1/2, за которое концентрация реагента уменьшится в 2 раза. По виду уравнения, связывающего t1/2 с константой скорости, можно судить о порядке реакции.

Одной из важнейших характеристик лекарственных препаратов является срок годности, представляющий собой время, за которое основное действующее лекарственное вещество в нём разложится не более, чем на 10%. Срок годности может быть определен с помощью кинетического уравнения реакции разложения данного вещества (при известной константе скорости).

Зависимость константы скорости от температуры выражается уравнением Аррениуса:

k = A e - E¹/RT,

где А – предэкспоненциальный множитель, зависящий от частоты столкновения частиц и их взаимной ориентации, Е¹ - энергия активации реакции, представляющая собой разность между энергией, необходимой для протекания данной реакции, и средней энергией молекул исходных веществ.

Чтобы избавиться от трудно определяемого коэффициента А, уравнение Аррениуса в логарифмической форме дифференцируют по температуре и затем интегрируют в интервале температур от Т1 до Т2. При этом получается выражение:

где k1 и k2 – константы скорости реакции при температуре Т1 и Т2 соответственно, R - универсальная газовая постоянная.

Графическим отображением уравнения Аррениуса является прямая линия в координатах ln k - 1/T (аррениусовская зависимость). Эта зависимость лежит в основе определения сроков годности лекарств в растворах методом ускоренного старения. Метод заключается в том, что определяется несколько констант скорости реакции разложения лекарственного вещества при высоких температурах (когда в соответствии с правилом Вант-Гоффа скорость разложения резко возрастает) и затем с помощью экстраполяции находится k при температуре хранения. Исходя из её значения рассчитывается срок годности.

Вопросы для самоподготовки

1.   Предмет химической кинетики. Её значение для фармации, медицины, биологии.

2.   Скорость химической реакции. Размерность скорости. Истинная (мгновенная) и средняя скорость.

3.   Кинетическая классификация химических реакций. Молекулярность и порядок реакции (по данному веществу и в целом).

4.   Способы определения порядка реакции.

5.   Зависимость скорости реакции от концентрации реагентов. Закон действующих масс. Константа скорости.

6.   Реакции 1-го порядка. Вывод кинетического уравнения. Время полупревращения.

7.   Расчет сроков годности лекарственных препаратов. Метод ускоренного старения.

8.   Реакции 2-го порядка. Кинетические уравнения: а) для случая равных и б) для случая неравных концентраций реагентов. Время полупревращения.

9.   Зависимость скорости реакции от температуры. Правило Вант-Гоффа. Температурный коэффициент скорости.

10. Основные положения теории активных столкновений. Энергия активации реакции. Лимитирующая стадия.

11. Уравнение Аррениуса (вывод). Расчет энергии активации. Расчет констант скорости реакции при различных температурах.

12. Основные положения теории переходного состояния. Активированный комплекс. Энергетический профиль реакции.

13. Сложные реакции (последовательные, цепные, параллельные, сопряжённые). Примеры сложных реакций.

14. Особенности протекания гетерогенных реакций. Примеры. Реакции с диффузионным и кинетическим контролем.

15. Фотохимия. Фотохимические реакции (примеры). Основные законы фотохимии (закон Гротгуса - Дрейпера, закон Бунзена - Роско, закон Штарка - Эйнштейна). Фотохимические реакции в фармации.

16. Световая и темновая стадии фотохимических реакций. Фотосенсибилизация. Квантовый выход реакций.

17. Катализ. Значение катализа в фармации и биологии. Виды катализа (гомогенный и гетерогенный). Катализаторы, ингибиторы, промоторы, каталитические яды.

18. Механизм действия катализатора. Его влияние на энергию активации реакции. Примеры гомогенного катализа. Кислотно-основный катализ в фармации и биологии.

19. Гетерогенный катализ. Активные центры. Мультиплетная теория Баландина.

20. Катализ на носителях. Теория активных ансамблей Кобозева.

21. Ферментативный катализ. Ферменты.

Решение типовых задач.

Задача 1. При гидролизе этилхлорида, содержащегося в фармпрепарате “Хлористый этил”, в 80%-ном водном растворе этанола концентрация его меняется во времени следующим образом:

Определите порядок реакции, константу скорости и время полупревращения.

Решение: Для определения порядка реакции рассчитаем значения константы скорости для различных промежутков времени. Исходя из предположения о наиболее простом случае, расчет проведем по кинетическому уравнению для реакции 1-го порядка:

Подставляем значения для каждого времени:

k1 = (1/4) ln (0,3115/0,258) = 0,04711 час-1;

k2 = (1/10) ln (0,3115/0,194) = 0,04735 час-1;

k3 = (1/27) ln (0,3115/0,085) = 0,04810 час-1 ;

k4 = (1/67) ln (0,3115/0,013) = 0,04741 час-1.

Поскольку значения k мало отличаются, примем, что порядок реакции первый (если бы значения k отличались значительно, расчет следовало бы провести по кинетическому уравнению 2-го порядка).

Константу скорости рассчитаем как среднее арифметическое из полученных значений:

k = (0,04711 + 0,04735 + 0,04810 + 0,04741) /4 = 0,04749 час-1.

Время полупревращения t1/2 можно рассчитать по кинетическому уравнению, заменяя Сt на соответствующее ему значение С0/2:

Подставляем значения:

t1/2 = 0,693/0,04749 = 14,592 час = 14 час 36 мин.

Задача 2. Вычислите срок годности инъекционного раствора, если константа скорости разложения лекарственного вещества в нём при 60оС равна 1,64´10-6 с-1 , а при 90оС – 4,2´10-6 с-1.

Решение: Для расчета срока годности нужно знать константу скорости разложения вещества при 20оС. Воспользуемся для её нахождения уравнением Аррениуса:

где k1 и k2 - константы скорости соответственно при температурах T1 и T2 (в К); E¹ - энергия активации реакции; R - универсальная газовая постоянная.

Сначала найдем значение энергии активации:

Зная E¹ , можно определить константу скорости при 20оС k20 (принимая, что k1 = k90) по этому же уравнению:

k90/k20 = e2,494 = 12,107;

отсюда k20 = k90 /12,107 = 4,2´10-6/12,107 = 3,47´10-7 c-1.

Считая, что разложение препарата идет по кинетике первого порядка, рассчитаем срок годности t1/10 как время разложения на 10%:

Задача 3. Содержание изотопа 14С в бивне мамонта составляет 5,25% от его содержания в живых тканях растительности на месте находки. Сколько времени прошло после гибели мамонта? Период полураспада 14С 5600 лет.

Решение: Считая, что изотоп 14С распадается по кинетике 1 порядка, рассчитаем время по соответствующему уравнению (см. Задачу 1). Сначала найдем константу скорости распада 14С:

Зная k, определим искомое время:

Задача 4. Реакция между веществами А и В выражается уравнением 2А + В = C. Начальная концентрация А равна 3,2 моль/л, а В - 1,6 моль/л. Константа скорости равна 0,75 мин-1.Какова скорость реакции а) в начальный момент; б) по истечении некоторого времени, когда концентрация А уменьшилась на 0,5 моль/л? Как изменится начальная скорость, если концентрации увеличить в 2 раза?

Решение: Воспользуемся уравнением закона действующих масс (считая, что порядок реакции по каждому веществу соответствует его стехиометрическому коэффициенту):

v = k CA2 CB.

Тогда

а) v0 = 0,75´3,22´1,6 = 12,288 моль/(л · мин).

б) при уменьшении СА на 0,5 моль/л в соответствии с уравнением реакции CB уменьшится на 0,25 моль/л. Скорость реакции при этом будет равна

v = 0,75 (3,2-0,5)2´(1,6-0,25) = 7,38 моль/(л · мин).

При увеличении концентраций реагентов в 2 раза скорость реакции станет равной

v = k (2СА)2 (2СВ) = 8 k СА2 СВ, т. е. увеличится в 8 раз.

Задачи для самостоятельного решения

Задача 1. Как изменится скорость реакции, идущей по уравнению 2Н2 + О2 = 2Н2О, если давление увеличить в 3 раза?

Ответ: увеличится в 27 раз.

Задача 2. Найти среднее значение константы скорости реакции (1 порядка) разложения Н2О2 в водном растворе, а также определить время полупревращения и время разложения H2O2 на 90%, если на титрование одинаковых проб раствора израсходованы следующие объёмы раствора КMnO4:

Ответ: kср = 0,0554; 12,5 мин; 41,56 мин.

Задача 3. При гидролизе сахарозы образовались глюкоза и фруктоза. При этом произошло следующее изменение угла вращения плоскости поляризации при 25оС в присутствии 0,5 н. HCl:

Вычислить: 1) константу скорости реакции; 2) сколько сахарозы (в %) инвертируется в течение 250 мин.

Ответ: 1) k = 5,06´10-3; 2) 71,8%.

Задача 4. Как возрастет скорость реакции при повышении температуры от 20оС до 100оС, если температурный коэффициент скорости равен 2?

Ответ: в 256 раз.

Задача 5. Для реакции разложения HI константа скорости при 280оС равна 7,96´10-7, а при 300оС – 3,26´10-6 мин-1. Рассчитать энергию активации, константу скорости при 290оС и температурный коэффициент реакции в указанном интервале температуры.

Ответ: Е¹ = 185,6 кДж/моль; k = 1,63´10-6; g = 2,02.

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8 9 10