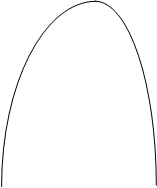
T, oC T, oC 70 70   60 60 50 50 40 40 30 30 20 20   0 фенол вода 0 состав, масс. %

15. Провести конноды, отвечающие температурам 40, 45, 50, 60, 65оС (или другим, указанным преподавателем), как показано на рисунке. Определить составы сопряжённых растворов при температурах, указанных преподавателем.

16. Найти и отметить точки, отвечающие среднему арифметическому из составов сопряжённых фаз, которые находятся точно в середине каждой конноды. Провести прямую линию, соединяющую середины коннод, и продлить её до пересечения с кривой расслоения. Определить критическую температуру растворения системы. Установить, подчиняется ли данная система правилу Алексеева.

17. Занести расчетные данные в таблицу.

18. Сформулировать выводы.

Работа 2.4. Определение коэффициента распределения третьего компонента между двумя жидкими фазами.

Цель работы: Определение коэффициента распределения третьего компонента между водой и органическим растворителем путем проведения жидкостной экстракции.

Целевые задачи: Проведение жидкостной экстракции третьего компонента из водного раствора органическим растворителем; титриметрическое определение концентрации третьего компонента в обеих фазах системы; расчет коэффициента распределения и степени ассоциации вещества в органическом растворителе; оценка экстракционной эффективности органического растворителя.

Если в систему из двух несмешивающихся жидкостей ввести небольшое количество третьего компонента, то после установления равновесия он окажется в обеих фазах, но в разном количестве. Для каждой температуры отношение концентраций третьего компонента в двух равновесных жидких фазах является величиной постоянной, независимо от этих концентраций (закон распределения Нернста):

где К - коэффициент распределения.

Закон распределения является теоретической основой жидкостной экстракции. Экстракцией из растворов называется извлечение и разделение компонентов раствора путем перевода их из одной жидкой фазы в другую, содержащую экстрагент. Основными условиями экстракции являются:

а) несмешиваемость экстрагента с исходным раствором,

б) отсутствие химического взаимодействия извлекаемого вещества с экстрагентом,

в) намного большая растворимость извлекаемого вещества в экстраген - те, чем в первоначальном растворителе.

Фаза, в которую после экстракции переходит извлекаемое вещество, называется экстрактом, а фаза, обедненная им - рафинатом.

Количественной характеристикой эффективности экстракции является коэффициент распределения. В данных методических указаниях выбрана такая система обозначений: С1 - концентрация извлекаемого вещества в рафинате, С2 - его концентрация в экстракте. При этом чем меньше значение коэффициента распределения, тем эффективнее экстрагент и тем больше степень извлечения третьего компонента. Она определяется как отношение массы извлекаемого вещества в экстракте к его массе, содержавшейся в исходном растворе до экстракции.

В ряде случаев при переходе третьего компонента через поверхность раздела фаз его средняя молярная масса изменяется вследствие ассоциации или диссоциации в одном из растворителей. В таких случаях уравнение закона распределения можно представить в виде

где n - показатель при данной температуре, обусловленный свойствами

всех трех компонентов системы, и представляющий собой отношение средних молярных масс третьего компонента в исходном растворителе и в экстрагенте. Например, если уксусная кислота в воде существует главным образом в виде отдельных молекул, а в бензоле - в виде ассоциатов из двух молекул (димеров), то:

Из методов определения К наиболее употребителен графический. Его принцип заключается в следующем. Уравнение (1) путем логарифмирования линеаризуется, т. е. преобразуется в уравнение прямой, не проходящей через начало координат:

lgC1 = lgK + n lgC2 .

Затем по экспериментальным данным строится график зависимости lgC1 от lgC2, отсекающий от оси ординат отрезок, равный lgK. Тангенс угла наклона этого графика к оси абсцисс равен n. (подробнее об этом см. «Проведение опыта»).

Оснащение рабочего места

Пипетка на 1 мл. Склянки с пробками на 100 мл.

Колбы для титрования. Раствор NаОН 0,1 н.

Цилиндр на 10 мл. Бюретка на 25 мл.

Раствор фенолфталеина в спирте.

Растворы экстрагируемого вещества и органические растворители (по указанию преподавателя).

Проведение опыта

1.   Проверить оснащение рабочего места.

2.   Измерить и записать температуру.

3.   В три склянки с притертыми пробками поместить по 10 мл водных растворов экстрагируемого вещества кислотной природы (по указанию преподавателя).

4.   Добавить к каждому раствору по 10 мл указанного преподавателем органического растворителя (под тягой!).

5.   Склянки плотно закрыть пробками и после интенсивного встряхивания в течение трех минут оставить для перераспределения не менее чем на 20 минут.

6.   Определить титрованием концентрацию экстрагируемого вещества во всех исходных растворах (обозначается С0I, С0II и С0III) для чего отмерить 1 мл исходного раствора экстрагируемого вещества в колбу для титрования, затем добавить 1 каплю раствора фенолфталеина и титровать 0,1 н. раствором NaOH до появления слабо-розового окрашивания, не исчезающего в течениесекунд. Повторить титрование трижды для каждого раствора. Рассчитать С0I, С0II и С0III по уравнению:

где VNaOH - объём раствора NaOH, пошедший на титрование (среднее арифметическое из результатов трех титрований), CNaOH - концентрация NaOH, моль-экв/л, Vк - объём раствора экстрагируемого вещества, взятый для титрования (в данном случае – 1 мл).

Данные занести в таблицу 1.

7.   После установления экстракционного равновесия определить равновесные концентрации экстрагируемого вещества С1I, С1II и С1III в водном слое (рафинате). Для этого из склянок отобрать пипеткой по 1 мл водных растворов экстрагируемого вещества (нижний слой) в колбы для титрования и оттитровать 0,1 н. раствором NaOH. Титрование провести трижды для каждого раствора (все результаты титрования сверить у преподавателя). Для расчета использовать уравнение (2).

8.   По разности С0 – С1 = С2 вычислить равновесные концентрации экстрагируемого вещества С2I, С2II и С2III в органическом слое (экстракте). Данные сверить у преподавателя и занести в таблицу 1.

9.   Рассчитать логарифмы С1 и С2 (с точностью до четырех десятичных

знаков) и занести данные в таблицу 1.

11. Построить график зависимости lgC1 от lgC2 (см. рис.) и продлить его до пересечения с осью Y. При этом от неё отсекается отрезок ОВ, равный lgК, а тангенс угла наклона графика к оси Х равен n.

lg C1 B   0 lg C2   A C

Рассчитать коэффициент распределения К = 10ОВ. Построить прямоугольный треугольник АВС (так, чтобы отрезки ВС и АС были как можно больше для повышения точности расчета). Рассчитать степень ассоциации экстрагируемого вещества в экстрагенте n = BC/AC.

12. Рассчитать по уравнению (1) К для каждого опыта (КI, КII и КIII) и вычислить среднее арифметическое. Сравнить это значение с найденным графически. Все расчетные данные занести в таблицу 2.

13. Привести в порядок рабочее место и сдать его дежурному.

Таблица 2.

14. Сформулировать выводы.

4. Буферные растворы в фармации. Механизм буферного действия. Связь рН буферных растворов с их составом. Буферная ёмкость.

5. Активность ионов и её связь с концентрацией электролита. Коэффициент активности. Константа диссоциации слабых электролитов. Степень диссоциации. Закон разведения Оствальда. Вывод его математического выражения.

6. Удельная и эквивалентная (мольная) электрическая проводимость растворов. Зависимость электропроводимости от различных факторов. Подвижность ионов. Закон Кольрауша.

7. Кондуктометрическое определение степени и константы диссоциации слабых электролитов.

8. Кондуктометрическое титрование.

Решение типовых задач.

Задача 1. Удельная электрическая проводимость 0,175 М раствора аммиака равна 0,476 Ом-1см-1. Подвижности ионов NH4+ и ОН– при 25оС соответственно равны 73,5 и 198,3 Ом-1см2моль-1. Рассчитать молярную проводимость, степень и константу ионизации аммиака рКb, концентрацию ионов водорода в растворе и его рН.

Решение: Удельная k и молярная l электрические проводимости связаны между собой соотношением l = k/С, где С – концентрация в моль/л.

Рассчитываем l:

Степень ионизации вычисляется с помощью уравнения: a = l/l¥, где l¥ – мольная (эквивалентная) проводимость при бесконечном разведении, которую определяют по закону Кольрауша: l¥ = l+ + l, (где l+ и l- – подвижности ионов).

l¥ = 73,5 + 198,3 = 271,8 Ом-1см2моль-1,

отсюда: a = 2,72/271,8 = 0,01.

В соответствии с законом разведения Оствальда

где К - константа ионизации электролита (в данном случае К = Кb аммиака), С - концентрация в моль/л,

Отсюда рКb = - lg Кb = 4,752.

Концентрация ионов ОН - в растворе будет равна aС:

Сон- = 0,01´0,175 = 0,00175 моль/л.

Отсюда рОН = - lg 0,00175 = 2,76; рН =,76 = 11,24.

Задачи для самостоятельного решения.

Задача 1. Эквивалентная электрическая проводимость при бесконечном разведении пикрата калия при 25оС равна 1,0397 Ом-1см2моль-1. Подвижность иона калия 0,7358 Ом-1см2моль-1 . Рассчитать подвижность пикрат-иона. Какова будет эквивалентная электрическая проводимость раствора при степени диссоциации пикрата калия, равной 0,2?

Ответ: 0,3039 Ом-1см2моль-1; 0,2079 Ом-1см2моль-1.

Задача 2. Эквивалентная электрическая проводимость 0,117 М раствора уксусной кислоты при 25оС равна 4,815 Ом-1см2моль-1. Рассчитать степень диссоциации СН3СООН в этом растворе и константу диссоциации, если подвижность ионов водорода и ацетата при 25оС, соответственно, равны 349,8 и 40,9 Ом-1см2моль-1.

Ответ: 0,0123; 1,75´10-5.

РАБОТА 3.1.

Определение константы и степени диссоциации (ионизации) слабых электролитов в водных растворах.

Цель работы: определение степени и константы диссоциации (ионизации) слабых электролитов кондуктометрическим методом.

Целевые задачи: Освоение кондуктометрического метода; расчет константы ячейки (ёмкости сопротивления); измерение сопротивления растворов слабых электролитов; определение удельной и молярной электрической проводимости, степени и константы ионизации растворов электролитов.

Электрическая проводимость раствора – свойство, характеризующее способность проводить электрический ток. Она зависит от количества и природы ионов, природы растворителя и температуры раствора. Измерение электрической проводимости лежит в основе метода исследования и анализа, называемого кондуктометрией. Различают прямую кондуктометрию и кондуктометрическое титрование.

В прямой кондуктометрии по электрической проводимости находят степень и константу диссоциации электролитов, константу устойчивости комплексных соединений, произведение растворимости солей и т. д.

При кондуктометрическом титровании по изменению электрической проводимости контролируют ход взаимодействия титранта с определяемым веществом и находят эквивалентные точки реакций нейтрализации, осаждения, окисления – восстановления и др.

Электрическую проводимость определяют по сопротивлению, которое измеряют с помощью установки, состоящей из измерительного прибора - кондуктометра и кондуктометрической ячейки.

Растворы электролитов характеризуются удельной и эквивалентной электрическими проводимостями.

Удельная электрическая проводимость k – величина, обратная удельному сопротивлению раствора r (которое можно рассчитать, зная общее сопротивление R, длину и площадь поперечного сечения проводника: r = RS/l): k= 1/r. Размерность её в системе СИ Ом-1м-1, однако в практических расчетах обычно используется размерность Ом-1см-1. Физический смысл k при этом будет таким: проводимость объёма раствора, заключенного между двумя плоскими параллельными электродами (площадь поверхности каждого из которых равна 1 см2), расположенными на расстоянии 1 см друг от друга.

Эквивалентная (мольная) электрическая проводимость l - проводимость объёма раствора, содержащего 1 моль эквивалента исследуемого вещества, и заключенного в объёме между плоскими параллельными электродами, расположенными на расстоянии 1см друг от друга. Размерность l в системе СИ Ом-1м2моль-1, однако пользуются и другой размерностью (Ом-1см2моль-1).

Эквивалентная и удельная электропроводимости связаны между собой уравнением:

l = kV,

где V – разведение, то есть объём (в см3) раствора, в котором содержится 1 моль эквивалента исследуемого электролита.

Так как V = 1/С (где С – концентрация), то, при выражении концентрации в моль/л, получается соотношение

l = (k·1000)/С, (3.1)

где 1000 – пересчетный коэффициент из л в см3.

Проводимость растворов зависит от концентрации, температуры, природы растворенного вещества и растворителя, вязкости, диэлектрической проницаемости и других факторов. Поэтому для характеристики свойств электролита в данном растворителе в кондуктометрии обычно используют эквивалентную (мольную) электрическую проводимость при бесконечном разведении l¥. Она представляет собой предел, к которому стремится l с ростом разведения (или с уменьшением концентрации, стремящейся к нулю).

В соответствии с законом Кольрауша l¥ может быть рассчитана как сумма ионных электрических проводимостей при бесконечном разведении (или, иначе, подвижностей ионов):

l¥ = l+ + l- .

Устройство кондуктометра и принцип его действия

Кондуктометр состоит из измерительного прибора и кондуктометрической ячейки, в которую помещается исследуемый раствор электролита. Ячейка представляет собой стеклянный сосуд с вмонтированными в него электродами.

Для прецизионных (высокоточных) измерений используются платиновые электроды, покрытые для увеличения поверхности слоем тонкодисперсной платины (платиновой чернью). При менее точных измерениях, в т. ч. для учебных целей, можно использовать электроды из других металлов (инертных по отношению к исследуемому раствору).

Поскольку невозможно изготовить ячейки с одинаковыми характеристиками, для получения соизмеримых результатов надо для каждой ячейки определять поправочный коэффициент (т. н. константу ячейки). Константа находится с помощью измерения сопротивления данной ячейки, заполненной эталонным раствором с известной электропроводимостью, обычно 0,02 М раствором хлорида калия:

Кя = RKCl ·kKCl,

где kKCl - удельная проводимость раствора KCl при температуре опыта.

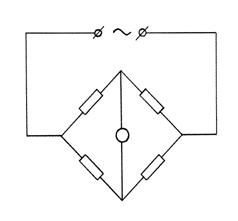
В основе конструкции кондуктометра лежит схема четырехплечного уравновешенного моста (мост Уитстона), изображенная на рисунке.

Ток, поступающий от источника в точку А, разветвляется к точкам В и D и затем через точку Е возвращается к источнику. Сопротивления отрезков АВ, ВЕ, АD и DЕ соответственно равны Rx, R3, R1, R2. Если к точкам В и D подключить нуль-индикатор (гальванометр) U, то в том случае, когда падения напряжения на участках АВ и АD и, соответственно, ВЕ и DЕ будут одинаковы, он покажет отсутствие тока. При этом будет иметь место соотношение

Rx/R3 = R1/R2,

называемое уравнением баланса моста. Сопротивления R1 и R2 выбираются так, чтобы они были одного порядка с измеряемым сопротивлением, а в качестве R3 берутся магазин сопротивлений и реохорд. Если известны сопротивления R1, R2, и R3, то можно определить и исследуемое сопротивление Rx.

Оснащение рабочего места

Кондуктометр Мерные цилиндры

Ячейка для измерения Колбы или стаканы на 50 мл

электропроводимости Бюретка на 50 мл

Раствор хлорида калия 0,02 М Термометр

Растворы слабых электролитов

Проведение опыта

1.   Проверить оснащение рабочего места. Измерить и записать температуру, при которой проводится опыт.

2.   Приготовить методом разбавления вдвое растворы слабого электролита (по указанию преподавателя). Для этого, например, отмерить в 4 колбы (пронумерованные от № 1 до № 4) по 30 мл дистиллированной воды. Добавить в 4-ю колбу 30 мл исходного раствора электролита. После тщательного перемешивания перенести последова­тельно по 30 мл раствора из 4-й колбы в 3-ю, из 3-й - во 2-ю, из 2-й - в 1-ю. В колбу № 5 отмерить 30 мл исходного раствора электролита.

3.   Подготовить к работе кондуктометр, для чего не менее 3 раз промыть дистиллированной водой ячейку кондуктометра; подключить её к клеммам «датчик»; установить ручку «термокомпенсация» в положение, соответствующее температуре опыта; включить прибор в сеть в соответствии с описанием и инструкцией.

4.   Для определения константы ячейки Кя поместить в ячейку эталонный 0,02 М раствор хлорида калия и измерить его сопротивление RKCl.

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8 9 10