Вещество | DНреш., кДж/моль |
NaCl | +774,0 |
KCl | +730,0 |
KBr | +677,5 |
KI | +637,5 |
9. Рассчитать моляльную концентрацию полученного раствора исследуемой соли:
n´1000 m = ¾¾¾¾ , А |
где А - масса воды в г, и найти в справочнике соответствующее ей значение DНр-р. Сравнить его с экспериментально найденным.
10. Сверить данные у преподавателя. Привести в порядок рабочее место и сдать его дежурному.
11. Сформулировать выводы.
РАБОТА 1.2.
Определение теплоты нейтрализации.
Цель работы: Определить теплоту нейтрализации сильной
кислоты сильным основанием или слабой кислоты сильным основанием.
Целевые задачи: Освоить технику термохимического эксперимента, определить графически изменение температуры в опыте, рассчитать теплоту нейтрализации:
а) В случае нейтрализации сильной кислоты сильным основанием рассчитать абсолютную и относительную экспериментальные ошибки;
б) В случае нейтрализации сильной кислоты слабым основанием рассчитать теплоту ионизации слабого основания.
Оснащение рабочего места
Калориметр Термометр
Магнитная мешалка Секундомер
Цилиндр на 20 мл
Растворы HCl, CH3COOH, NaOH, NH4OH - 1н.
Проведение опыта
1. Проверить оснащение рабочего места.
2. Отмерить цилиндром 15 мл 1 н. раствора кислоты, указанной преподавателем, перенести кислоту в калориметрический сосуд. Опустить в сосуд магнитный стержень, закрыть его пробкой с вставленным термометром и включить магнитную мешалку.
3. В другой цилиндр отмерить 15 мл 1н. раствора сильного или слабого основания (по указанию преподавателя) и поместить его в непосредственной близости от калориметрической установки.
4. После установления теплового равновесия (через 10 минут от начала перемешивания раствора кислоты в калориметре) начать отсчет температуры.
5. Отсчет проводить в течение 5 минут с интервалом 1 мин. (предварительный период).
6. Не прекращая перемешивания перенести раствор основания в калориметрический сосуд.
7. Произвести отсчеты температуры на 6-ой минуте (главный период), и далее вплоть до 10 мин. (заключительный период).
8. Результаты сверить у преподавателя и занести в таблицу.
9. Привести в порядок рабочее место и сдать его дежурному. Приступить к расчетам.
Примечание: Во избежание потери магнитного стержня раствор из калориметрического сосуда необходимо выливать в кристаллизатор. |
10. Построить график, отражающий зависимость температуры опыта от времени. Отрезок ВС, соединяющий точки, отвечающие температурам, измеренным на 5-ой и 6-ой минутах, разделить пополам (точка L). Провести через точку L вертикальную линию. Соединить точки начального и заключительного периодов усредняющими прямыми (АВ и СД). Продлить их до пересечения с вертикалью в точках К и М.
11. Определить по графику изменение температуры DT в опыте, соответствующее отрезку КМ.
K
· L
А В М
t, мин |
12. Рассчитать теплоту нейтрализации по формуле:
DНнейтр = -(w DT)/n,
где w - тепловое значение калориметра, DТ - изменение температуры в опыте, n - число молей одноосновной кислоты или основания.
Так как в ходе реакции нейтрализации теплота выделяется, то, согласно термодинамическим правилам записи, её значению приписывается знак “минус”.
Примечание: Тепловое значение калориметра w указывается преподавателем или определяется в специальных опытах с навеской KCl, как описано в работе 1.1. |
16. В случае определения теплоты нейтрализации сильной кислоты сильным основанием, рассчитать абсолютную и относительную ошибки опыта, сравнивая полученные значения со справочными. Для этого, используя данные справочной таблицы, построить график зависимости DНнейтр от температуры и с его помощью определить значение DНнейтр, теор, соответствующее температуре опыта Т. (В качестве Т принимается среднее значение температуры в начальном периоде).
Теплота нейтрализации сильной кислоты сильным основанием при различных температурах. | |
Т, К | DНнейтр, кДж/моль |
283 | -58,70 |
288 | -57,80 |
293 | -56,90 |
298 | -55,90 |
303 | -54,75 |
17. В случае определения теплоты нейтрализации слабой кислоты сильным основанием (или сильной кислоты слабым основанием) рассчитать теплоту диссоциации (ионизации) соответственно слабого основания или слабой кислоты:
DНдисс = DНнейтр слаб – DНнейтр сильн
18. Сформулировать выводы.
Тема 2. Фазовое равновесие.
Учение о фазовом равновесии рассматривает вопросы, связанные с физико-химией фазовых переходов (испарение, кипение, сублимация, плавление, отвердевание, конденсация пара, растворение, кристаллизация из растворов, экстракция и т. д.) в одно - и многокомпонентных системах. Уже из этого перечисления видна тесная связь учения о фазовом равновесии с фармацевтической практикой, в особенности в области фармацевтической технологии и анализа. Так, в частности, термодинамика фазовых переходов является теоретической базой перегонки (простой, фракционной, ректификации, перегонки с водяным паром), жидкостной экстракции, получения настоек, вымораживания и других процессов, применяемых при получении лекарственных веществ из растительного сырья. Определение с помощью термического анализа температур плавления эвтектических смесей лекарственных веществ позволяет предусмотреть их физическую совместимость или несовместимость. Изучение диаграмм плавления и свойств эвтектических смесей, образующихся при отвердевании двойных смесей, позволяет улучшить качество лекарств, повысить их биодоступность.
Закон распределения третьего компонента между двумя несмешивающимися жидкостями лежит в основе не только жидкостной экстракции, как технологического метода выделения веществ из растворов, но и распределительной хроматографии (в том числе хроматографии на бумаге). Коэффициент распределения веществ между водой и н-октанолом и его логарифм (параметр гидрофобности) являются важнейшими параметрами при изучении всасывания лекарственных веществ и проникновения их сквозь клеточные мембраны.
Изучив данную тему и выполнив лабораторные работы, относящиеся к ней, студент должен знать:
· основные понятия теории фазовых равновесий (фаза, компонент, число независимых компонентов, вариантность);
· правило фаз Гиббса;
· виды фазовых диаграмм и принципы их построения;
· законы Нернста, Рауля, Коновалова, Дальтона, правило Алексеева;
· физико-химические основы экстракции и различных видов перегонки;
· причины образования и свойства азеотропных растворов и эвтектических смесей.
Студент должен уметь:
¨ строить и анализировать диаграммы кипения, плавления, растворения;
¨ проводить жидкостную экстракцию;
¨ рассчитывать коэффициент распределения и степень ассоциации веществ в растворе;
¨ рассчитывать число операций экстрагирования, необходимых для достижения заданной степени извлечения растворенного вещества;
¨ определять температуру гетерогенизации и критическую температуру растворения жидкостных смесей;
¨ с помощью правила рычага определять соотношение масс различных фаз в гетерогенных системах;
¨ определять состав эвтектик и азеотропов и температуры их фазовых переходов;
¨ с помощью правила фаз рассчитывать вариантность (число степеней свободы) гетерогенных систем.
Студент должен приобрести или закрепить навыки:
* приготовления и отмеривания растворов;
* титрования;
* пользования термометрами;
* пользования справочной литературой;
* табулирования экспериментальных данных;
* построения и анализа графиков (диаграмм).
Вопросы для самоподготовки
1. Фазовое равновесие. Основные понятия (фаза, компонент, число независимых компонентов, вариантность системы, фазовые переходы). Правило фаз Гиббса.
2. Фазовые диаграммы (диаграммы состояния). Диаграмма состояния однокомпонентной системы и её анализ (на примере воды).
3. Уравнение Клапейрона для фазовых переходов (вывод).
4. Уравнение Клаузиуса - Клапейрона для процесса кипения (вывод).
5. Растворы. Способы выражения концентрации и соотношения между ними. Растворы в фармации.
6. Двухкомпонентные (бинарные) смеси летучих жидкостей. Идеальные растворы. Закон Рауля.
7. Реальные растворы. Отклонения от закона Рауля. Диаграммы кипения. 1-й закон Коновалова.
8. Простая перегонка и ректификация бинарных смесей.
9. 2-й закон Коновалова. Азеотропные смеси, их виды. Примеры. Способы разделения азеотропных смесей. Получение абсолютизированного спирта.
10. Ограниченно растворимые друг в друге жидкости. Диаграмма растворимости. Критическая температура растворения (КТР). Правило Алексеева.
11. Несмешивающиеся жидкости. Закон Дальтона. Перегонка с водяным паром. Уравнение для коэффициента расхода пара (вывод).
12. Третий компонент в системе из двух несмешивающихся жидкостей. Закон распределения Нернста. Коэффициент распределения. Жидкостная экстракция в фармации.
13. Уравнения для расчета массы растворенного вещества, переходящего в экстракт и остающегося в первоначальном растворе (вывод). Степень извлечения. Расчет числа операций экстрагирования для достижения заданной степени извлечения.
14. Диаграммы плавления бинарных смесей. Кривые охлаждения. Термический анализ.
15. Диаграммы плавления смесей веществ, образующих химические соединения. Диаграммы плавления тройных смесей.
16. Коллигативные свойства растворов неэлектролитов. Понижение (депрессия) температуры отвердевания растворов. Криоскопическая константа. Криометрическое определение молярной массы веществ.
17. Повышение температуры кипения растворов. Эбуллиоскопическая константа. Эбуллиоскопическое определение молярной массы веществ.
18. Осмос. Осмотическое давление растворов неэлектролитов и электролитов. Изотонический и осмотический коэффициенты. Уравнение Вант-Гоффа.
19. Изо-, гипо - и гипертонические растворы в фармации. Изотонирование. Осмометрическое определение молярной массы веществ.
Решение типовых задач
Задача 1. Для предотвращения частичного разложения лекарственного препарата в кипящем водном растворе при отгонке воды необходимо снизить температуру кипения на 20оС. Вычислить, какое давление при этом надо поддерживать в перегонном аппарате. Теплота испарения воды 40,66 кДж/моль.
р2 DН (Т2 - Т1) ln ¾ = ¾¾¾¾¾¾ , p1 R T1 T2 |
Решение. Используем для расчета уравнение Клапейрона-Клаузиуса:
где Т1 и Т2 - температуры кипения при давлениях р1 и р2 соответственно.
Считая, что при нормальном атмосферном давлении р2 =101325 Па температура кипения раствора Т2 » 100oС (373 К), подставим значения:
р2 40,66 ( ln ¾ = ¾¾¾¾¾¾¾¾¾ = 0,7428. p1 8,314´10-3´353´373 |
Отсюда ln p1 = ln 101325 – 0,7428 = 11,5261 – 0,7428 = 10,7833
и, значит, р1 = е10,7833 = 48208,95 Па = 0,48 атм.
Задача 2. В 100 г воды растворено 1,53 г глицерина. Давление пара воды при 298 К равно 31672 Н/м2 . Рассчитать понижение давления пара воды над раствором по сравнению с чистой водой.
Решение. По закону Рауля относительное понижение давления равновесного с раствором пара равно мольной доле Х растворенного вещества:
Dр/ро = Хгл,
откуда
Dр =Хглро,
где Хгл - мольная доля глицерина.
Так как Хгл = nгл/( nгл+nН2О), где n - количество вещества в молях
(nН2О = 100/18 = 5,555 моль; nгл = 1,53/92 = 0,0166 моль), то
Хгл = 0,0166/(0,0166 + 5,555) = 0,003.
И тогда Dр = 0,003´31672 = 95,016 Па (то есть давление пара воды над этим раствором на » 95 Па ниже, чем над чистой водой).
Задача 3. Рассчитать вариантность систем:
а) водный раствор NaCl и KCl + водяной пар + лед + кристаллы NaCl + кристаллы KCl.
б) водный раствор KOH и CO2 + водяной пар.
Решение: Вариантность (число степеней свободы) рассчитывается по правилу фаз Гиббса С = К - Ф + n, где К - число независимых компонентов, Ф - число фаз, n - число внешних факторов, влияющих на состояние системы. Для систем, на состояние которых влияют только температура и давление, n = 2.
а) В системе 3 компонента (вода и две соли), между которыми не происходит химической реакции, 5 фаз (раствор, пар, лед и кристаллы двух солей), значит
С = 3 – 5 + 2 = 0.
б) В этом случае в системе возможна реакция 2КОН + СО2 = К2СО3 + Н2О, при этом появляется еще один компонент К2СО3 . Число независимых компонентов равно общему числу компонентов минус число протекающих в системе реакций, и значит
С = ( 4 – 1 ) – 2 + 2 = 3.
Задача 4. С помощью диаграммы растворимости определить:
а) критическую температуру растворения (КТР) в системе “фенол + вода”;
б) температуру гомогенизации смеси, содержащей 70% фенола и 30% воды;
в) составы сопряжённых растворов при температуре 45оС;
г) пределы растворимости компонентов при температуре 37оС.
Решение:
а) КТР определяется по максимуму кривой растворения; КТР = 68оС.
б) нагревание этой смеси отображается движением фигуративной точки вверх по линии АВ. Точка С, соответствующая переходу из гетерогенной области в гомогенную, соответствует искомой температуре гомогенизации (» 41оС).
в) точки D и Е, отвечающие пересечению конноды (части изотермы, «стягивающей» ветви кривой) с ветвями линии расслоения при 45оС, позволяют определить составы D’ и Е’ сопряжённых растворов, сосуществующих при равновесии:
D’: 14% фенола + 86% воды; Е’: 69% фенола + 31% воды.
г) задание аналогично п. в) : при 37оС возможно существование гомогенных растворов, содержащих от 0 до »28% воды в фенольном растворе (область G) и от 0 до 12% фенола (область F).
Задача 5. В 1 л (V1) водного раствора содержится 0,15 г иода. Рассчитать:
а) сколько г иода будет извлечено из этого раствора при однократной экстракции с помощью 40 мл (V2) CСl4;
б) при четырехкратной экстракции порциями (V2)по 10 мл ССl4;
в) степень извлечения в обоих случаях;
г) число экстракций порциями по 10 мл ССl4 , необходимых для извлечения 99% иода.
Коэффициент распределения иода между водой и ССl4 К = 0,0117.
Решение.
а) Количество иода, экстрагированного при однократном извлечении:
КV1 0,0117´1000 mэ = mо [1 - (¾¾¾¾)] = 0,15[1 – (¾¾¾¾¾¾¾¾)] = 0,116 г. KV1+V2 0,0117´1000 + 40 |
б) Количество иода, экстрагированного при четырехкратном извлечении:
КV1 4 0,0117´1000 4 mэ = mо [1 - (¾¾¾¾) ] = 0,15[1 - (¾¾¾¾¾¾¾¾) ] = 0,137 г KV1+V2 0,0117´1000+10 |
в) Степень извлечения в первом случае: a1 = mэ/mо = 0,116/0,15 = 0,773 (или 77,3%).
Во втором случае: a2 = mэ /mо = 0,137/0,15 = 0,913 (или 91,3%).
КV1 n mэ = mо[1 - ( ¾¾¾¾) ] KV1+V2 |
г) решим уравнение для количества экстрагированного вещества
mэ КV1 n 0,0117´1000 n a = ¾¾ = 1 - (¾¾¾¾); 0,99 = 1 - (¾¾¾¾¾¾¾¾) ; mо KV1+V2 0,0117´1000 + 10 |
относительно числа экстракций (заменяя mэ/mо на a):
(0,5391)n = 1 - 0,99 = 0,01. Для удобства дальнейшего решения логарифмируем полученное выражение: n lg 0,5391 = lg 0,01.
Отсюда n = lg 0,01/lg 0,5391 = -2/-0,2683 = 7,46.
Поскольку возможно проведение только целого числа экстракций, примем n = 8.
Задача 6. В 100 г воды растворено 1,53 г глицерина (плотность глицерина 1,26 г/см3). Рассчитайте для этого раствора:
а) температуру кипения, б) температуру замерзания, в) осмотическое давление.
Решение.
Кэ m 1000 DТкип = ¾¾¾¾¾¾ , М а |
а) С помощью эбуллиоскопической формулы для раствора неэлектролита
где Кэ - эбуллиоскопическая константа растворителя (для воды она равна »0,52); m - масса растворенного вещества в г; М - его молярная масса; а - масса растворителя в г,
рассчитаем DТкип - повышение температуры кипения раствора по сравнению с чистым растворителем (водой):
0,52´1,53´1000 DТкип = ¾¾¾¾¾¾¾ = 0,086о. 92´100 |
Следовательно, температура кипения раствора будет равна 100 + 0,086 = 100,086 » 100,1оС.
б) Понижение (депрессию) температуры замерзания раствора неэлектролита найдем с помощью криоскопической формулы
Кк m 1000 DТкип = ¾¾¾¾¾¾ , М а |
где Кк - криоскопическая константа растворителя (для воды она равна 1,86):
1,86´1,53´1000 DТкип = ¾¾¾¾¾¾¾ = 0,310о. 92´100 |
Следовательно, температура замерзания раствора будет равна
0 - 0,310 = - 0,31оС.
в) В соответствии с законом Вант-Гоффа осмотическое давление p раствора неэлектролита может быть рассчитано по уравнению
p = СRТ,
где Т - абсолютная температура; R - универсальная газовая постоянная; С - молярная концентрация растворенного вещества (при расчетах в системе СИ она должна быть выражена в моль/м3). Считая плотность воды равной 1 г/см3, найдем объём раствора:
Vр-р = 1,53/1,26 + 100 = 101,21 см3 =0,10121 л.
Тогда
С = (1,53/92)´0,10121 = 0,164 моль/л = 0,164´103 моль/м3,
и
p = 0,164´103·8,314·298 = 8 Па (»4,06 атм).
Задача 7. Камфора С10Н16О перегоняется при нормальном атмосферном давлении и температуре 95оС с водяным паром. Рассчитайте а) коэффициент расхода водяного пара, б) массу водяного пара, необходимого для получения из сырья 15 кг камфоры.
Решение. а) Коэффициент расхода водяного пара mв/mк рассчитывается по уравнению
mв рв · Мв ¾¾ = ¾¾¾¾¾ , mк рк · Мк |
где рв и рк - парциальные давления паров воды и камфоры, Мв и Мк - их молярные массы.
Давление пара воды находим в справочнике: при 95оС оно равно 84525 Па; давление пара камфоры определим с помощью закона Дальтона, в соответствии с которым общее давление пара в системе из несмешивающихся компонентов равно сумме парциальных давлений пара каждого из компонентов. Так как общее давление пара равно атмосферному, т. е. 101325 Па, рк = 101= 16800 Па.
Отсюда
mв 84525 ´ 18 ¾ = ¾¾¾¾¾¾ = 0,596 , mк 16800 ´ 152 |
то есть для перегонки одного килограмма камфоры требуется 0,596 кг водяного пара.
б) Для получения 15 кг камфоры потребуется 15 ´ 0,596 =8,940 кг водяного пара.
Задачи для самостоятельного решения
Задача 1. Рассчитайте давление пара растворителя над раствором, содержащим 180 г воды и 68,4 г сахарозы, если при температуре 338 К давление пара над чистым растворителем равно 25003 Па.
Ответ: р = 24502,9 Па.
Задача 2. Рассчитайте температуру замерзания раствора, содержащего 0,9 л глицерина (плотность 1,261 г/см3) в 10 л воды. Криоскопическая константа воды 1,86.
Ответ: Òз = -2,29оС.
Задача 3. Для очистки анилина от примесей его перегоняют с водяным паром при нормальном атмосферном давлении и температуре 98,4оС. Давление пара воды при этом равно 96258,5 Па. Вычислить расход пара на 1 кг анилина.
Ответ: 3,67 кг пара.
Задача 4. Вычислите концентрацию иода в амиловом спирте, находящемся в равновесии с водным раствором, содержащим при 25оС 0,340 г/л иода. Коэффициент распределения иода между спиртом и водой К = 230.
Ответ: 78,2 г/л.
Задача 5. Коэффициент распределения салицилового альдегида между водой и тетрахлорметаном равен 0,0125. 0,5 л водного раствора салицилового альдегида с концентрацией 1,0 г/л взбалтывают с 0,02 л ССl4. Рассчитайте массу (г) экстрагированного салицилового альдегида и его концентрацию в водном растворе после экстракции.
Ответ: 0,381 г; 0,238 г/л.
Задача 6. Построить (схематически) диаграмму плавкости системы KCl – AgCl с одной эвтектикой по следующим данным: Тпл KCl 768оС, AgCl – 455оС, эвтектическая температура 310оС, состав эвтектики 70 мольн.% AgCl.
а) определить, что представляет собой система из 40 мольн.% AgCl и 60 мольн.% KCl;
б) какое вещество выкристаллизуется первым при охлаждении этой системы;
в) при какой температуре закончится кристаллизация системы? Чему равен состав последних её капель?
г) описать изменение состояния системы при охлаждении её до 250оС
д) каким будет фазовый состав той же системы, если её охладить до 450оС (при общей массе системы 3 кг)? Рассчитать по правилу фаз Гиббса вариантность этой системы (принимая n=1).
Ответ к пункту (д): 0,625 г кристаллов KCl, жидкая фаза 71 масс % AgCl; С = 1.
Задача 7. Для раствора, содержащего 3 г сахарозы в 50 г воды, рассчитать: а) температуру замерзания, б) температуру кипения.
Ответ: а) -0,3оС б) 100,1оС.
Задача 8. Рассчитать процентную концентрацию глюкозы в инъекционном растворе, который можно вводить внутривенно без дополнительного изотонирования.
Ответ: 5,41%.
Работа 2.1.
Построение диаграммы плавления бинарной смеси.
Цель работы: построение диаграммы плавления и её анализ.
Целевые задачи: освоение принципов построения диаграмм состояния двухкомпонентных систем и их анализа.
Если два твердых вещества смешать друг с другом в определенных пропорциях и смесь нагреть до высокой температуры, то, как правило, образуется однородная жидкость (расплав), представляющая собой раствор одного компонента в другом. При охлаждении такого расплава до определенной температуры он начнет кристаллизоваться, поскольку растворимость веществ друг в друге с понижением температуры уменьшается.
При кристаллизации жидких систем могут выделяться как чистые компоненты и образуемые ими химические соединения, так и твердые растворы. В зависимости от того, какая фаза выделяется из раствора, двухкомпонентные системы с неограниченной растворимостью в жидком состоянии могут быть разделены на типы, из которых для изучения лекарственных веществ наиболее важны следующие:
1. Без химических соединений и твердых растворов.
2. С образованием устойчивого химического соединения (плавящегося конгруэнтно).
3. С образованием неустойчивого химического соединения (плавящегося инконгруэнтно).
4. С неограниченной растворимостью компонентов в твердом состоянии.
Диаграммы состояния изображают равновесия между всеми фазами, образуемыми компонентами системы при различных концентрациях и температурах и при постоянном давлении. В случае изображения равновесий между расплавом и твердыми фазами такие диаграммы называются диаграммами плавления (плавкости).
Диаграммы плавления обычно строятся на основе данных термического анализа. Из способов термического анализа рассмотрим построение кривых охлаждения.
Кривые охлаждения строятся на основании эксперимента по охлаждению расплавленных веществ с непрерывным контролем температуры (см. рис.). Кривые охлаждения чистых веществ и эвтектических смесей имеют одну ступеньку, соответствующую их температуре кристаллизации (или плавления). На кривых охлаждения смесей кроме ступенек имеются изломы (см. рисунок ниже), отвечающие появлению кристаллов компонента, присутствующего в избытке (или их плавлению в случае нагревания).
а б г д е в
|
Кривые охлаждения: а - чистый компонент А; б - 10% компонента В; в - чистый компонент В; г -20% В; д -60% В; е - 80% В.
На основе данных, полученных с помощью кривых охлаждения строятся диаграммы плавления в координатах температура – состав:
Ж Тпл А
K L M
С Э Тв
А x состав В |
Диаграмма плавления: Э - эвтектическая точка; Л - линия ликвидуса; Тэ - температура эвтектики; С - линия солидуса; Ж - жидкая фаза; Тв - твердые фазы.

|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 10 |





 T,oC
T,oC



 Т, оС
Т, оС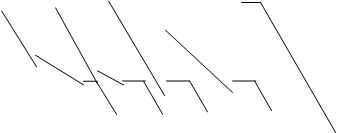
 Т
Т  Т
Т



