Глава третья
Радиаторная система охлаждения
3-1. Физические основы естественного масляного охлаждения
Эскиз контура охлаждения показан на рис. 3-1. Для наглядности путь движения масла, нагревающегося в активной части трансформатора и охлаждающегося в радиаторе, показан одной пунктирной линией. В дальнейшем процесс теплоотдачи объясняется процессами, происходящими в обмотке. Маслу, вошедшему в нижнюю часть обмотки в точке А, при прохождении по пути А - В вдоль обмотки передается в единицу времени количество теплоты Р. Это переданное с поверхности обмотки количество теплоты при средней теплоемкости масла с и массовом расходе масла G повысит температуру масла на ![]() . Тогда согласно уравнению теплового баланса
. Тогда согласно уравнению теплового баланса
![]() (3-1)
(3-1)
Поскольку плотность масла
![]() (3-2)
(3-2)
с повышением температуры уменьшается, нагретое масло поднимается вверх и на освобождаемое место снизу поступает холодное масло.
Нагретое масло в точке С входит в радиатор, где в единицу времени отдается окружающей среде количество теплоты Р. В результате масло охлаждается, его плотность возрастает и в точке D оно выходит из радиатора. Охлажденное масло в точке А вновь поступает в обмотку и процесс повторяется.
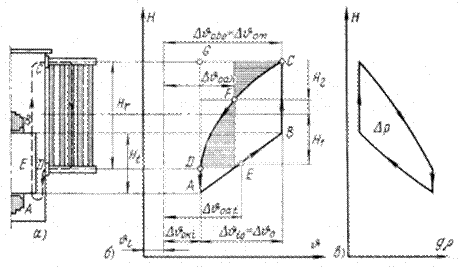
Рис. 3-1. К рассмотрению физических основ процесса естественной циркуляции масла.
а – эскиз контура циркуляции масла: б – диаграмма распределения температуры масла ![]() в контуре циркуляции в системе координат
в контуре циркуляции в системе координат ![]() ; в - диаграмма распределения удельного веса масла
; в - диаграмма распределения удельного веса масла ![]() в контуре циркуляции, в системе координат
в контуре циркуляции, в системе координат 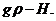
В установившемся режиме графическое изображение данного процесса в системе координат ![]() представляет собой замкнутую кривую (рис. 3-1,б), которую будем называть диаграммой распределения температур в контуре циркуляции масла или сокращенно температурной петлей.
представляет собой замкнутую кривую (рис. 3-1,б), которую будем называть диаграммой распределения температур в контуре циркуляции масла или сокращенно температурной петлей.
Если для масла известна зависимость
![]() (3-3)
(3-3)
то процесс нагревания и охлаждения масла может быть изображен в виде зависимости 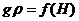 , где g – нормальное ускорение свободного падения,
, где g – нормальное ускорение свободного падения, ![]() - удельный вес масла (рис. 3-1, в). В установившемся режиме на различных высотах замкнутого контура охлаждения температура будет разная, соответственно будет меняться и плотность масла, т. e. она будет функцией высоты. Зависимость
- удельный вес масла (рис. 3-1, в). В установившемся режиме на различных высотах замкнутого контура охлаждения температура будет разная, соответственно будет меняться и плотность масла, т. e. она будет функцией высоты. Зависимость ![]() является замкнутой кривой, которую будем называть диаграммой распределения удельного веса масла в контуре циркуляции или сокращенно петлей давления. Данный процесс аналогичен процессу гравитационного водяного отопления. Площадь, охваченная кривой ABCDA, пропорциональна поддерживающей циркуляцию подъемной силе, т. е, гравитационному давлению, действующему в контуре циркуляции и обусловленному разностью холодного и нагретого масла. Кругооборот потока масла с кассовым расходом G обеспечивается за счет гравитационного давления:
является замкнутой кривой, которую будем называть диаграммой распределения удельного веса масла в контуре циркуляции или сокращенно петлей давления. Данный процесс аналогичен процессу гравитационного водяного отопления. Площадь, охваченная кривой ABCDA, пропорциональна поддерживающей циркуляцию подъемной силе, т. е, гравитационному давлению, действующему в контуре циркуляции и обусловленному разностью холодного и нагретого масла. Кругооборот потока масла с кассовым расходом G обеспечивается за счет гравитационного давления:
![]() (3-4)
(3-4)
Гравитационное давление ![]() уравновешивает возникающее при циркуляции масла гидравлическое сопротивление. Если пренебречь зависимостью удельной теплоемкости от температуры, то получим, что при отводе одного и того же количества теплоты в единицу времени произведение
уравновешивает возникающее при циркуляции масла гидравлическое сопротивление. Если пренебречь зависимостью удельной теплоемкости от температуры, то получим, что при отводе одного и того же количества теплоты в единицу времени произведение ![]() должно сохраняться постоянным [см. уравнение (3-1)]. При проектировании трансформатора стремятся
должно сохраняться постоянным [см. уравнение (3-1)]. При проектировании трансформатора стремятся ![]() , т. е. осевой перепад температуры масла в активной части, сделать минимальным с тем, чтобы нормированное стандартами наибольшее превышение температуры масла было ненамного больше превышения средней температуры масла в радиаторе
, т. е. осевой перепад температуры масла в активной части, сделать минимальным с тем, чтобы нормированное стандартами наибольшее превышение температуры масла было ненамного больше превышения средней температуры масла в радиаторе ![]() и чтобы соответственно можно было увеличить логарифмическую разность температур
и чтобы соответственно можно было увеличить логарифмическую разность температур ![]() в радиаторе (См. формулу (3-6), согласно которой с уменьшением
в радиаторе (См. формулу (3-6), согласно которой с уменьшением 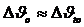 происходит увеличение
происходит увеличение ![]() , что позволяет при заданных потерях уменьшить площадь теплоотдающей поверхности радиатора)), существенно влияющую на его массу и стоимость. Малое значение
, что позволяет при заданных потерях уменьшить площадь теплоотдающей поверхности радиатора)), существенно влияющую на его массу и стоимость. Малое значение ![]() можно получить, если увеличить G. Для увеличения G необходимо снизить гидравлическое сопротивление контура циркуляции или увеличить
можно получить, если увеличить G. Для увеличения G необходимо снизить гидравлическое сопротивление контура циркуляции или увеличить ![]() .
.
Определение гравитационного давления
Значение ![]() определяется из петли давления по уравнению
определяется из петли давления по уравнению
![]() (3-5)
(3-5)
Параметр 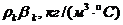 представляет собой изменение плотности масла, вызванное изменением температуры на
представляет собой изменение плотности масла, вызванное изменением температуры на ![]() и отнесенное к средней температуре масла
и отнесенное к средней температуре масла ![]() .
.
Упрощенная температурная петля изображена на рис. 3-1,б. На участке A-B в обмотке высотой ![]() масло нагревается, на участке C-D в радиаторах высотой
масло нагревается, на участке C-D в радиаторах высотой ![]() (расстояние между осями присоединительных патрубков) масло охлаждается. Принято, что на участке А-В температура изменяется по линейному закону, т. е. предполагается, что количество теплоты, передаваемое маслу в единицу времени с единицы длины пути (Вт/м), не изменяется с изменением температуры и что удельная теплоемкость масла также остается постоянной.
(расстояние между осями присоединительных патрубков) масло охлаждается. Принято, что на участке А-В температура изменяется по линейному закону, т. е. предполагается, что количество теплоты, передаваемое маслу в единицу времени с единицы длины пути (Вт/м), не изменяется с изменением температуры и что удельная теплоемкость масла также остается постоянной.
Характерной точкой участка А-В является точка Е, называемая центром нагрева, которая соответствует середине высоты обмотки и в которой циркулирующее в обмотке масло имеет превышение температуры, равное превышению средней температуры масла над температурой воздуха ![]() Форма кривой участка С-D соответствует конденсаторному распределению температуры, т. е. такому температурному распределению, которое возникает в том случае, когда теплоемкость одной из участвующих в теплообмене сред, в данном случае воздуха, принимается равной бесконечности. Характерной точкой этом кривой является точка F, называемая центром охлаждения, в которой температура масла отличается от температуры воздуха в радиаторе, принимаемой постоянной во всем радиаторе и равной
Форма кривой участка С-D соответствует конденсаторному распределению температуры, т. е. такому температурному распределению, которое возникает в том случае, когда теплоемкость одной из участвующих в теплообмене сред, в данном случае воздуха, принимается равной бесконечности. Характерной точкой этом кривой является точка F, называемая центром охлаждения, в которой температура масла отличается от температуры воздуха в радиаторе, принимаемой постоянной во всем радиаторе и равной ![]() , на логарифмическую разность температур
, на логарифмическую разность температур ![]() (См. рис. 3-19)
(См. рис. 3-19)
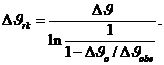 (3-6)
(3-6)
Точка F: находится выше середины высоты радиаторов на размер ![]() . Расстояние между серединами высот обмотки и радиатора обозначается через
. Расстояние между серединами высот обмотки и радиатора обозначается через ![]() . Разность высот точек E: и F
. Разность высот точек E: и F
![]() (3-7)
(3-7)
Площадь температурной петли (см. рис. 3-1,6):
![]() (3-8)
(3-8)
Определим размер ![]() . Для этого найдем площадь
. Для этого найдем площадь ![]() фигуры CDGC (Здесь учтено, что при конденсационном распределении температуры
фигуры CDGC (Здесь учтено, что при конденсационном распределении температуры ![]() ):
):
![]() (3-9)
(3-9)
Поскольку
![]()
можно написать:
![]()
Так как площадь петли CDGC равна площади прямоугольника, имеющего основание ![]() и высоту
и высоту ![]() , то
, то
![]() (3-10)
(3-10)
Найдем отсюда ![]() :
:
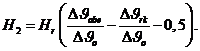 (3-11)
(3-11)
Площадь температурной петли
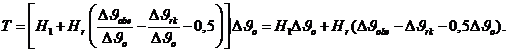 (3-12)
(3-12)
Тогда согласно уравнению (3-5) гравитационное давление
![]() (3-13)
(3-13)
Пример 3-1. Трансформатор мощностью ![]() с сочетанием напряжении
с сочетанием напряжении ![]() имеет масляное охлаждение с дутьем и естественной циркуляцией масла. При нагрузке до 70% номинального тока циркуляция воздуха также естественная. При нагрузке 70% потери короткого замыкания в процентах номинальных потерь короткого замыкания составляют
имеет масляное охлаждение с дутьем и естественной циркуляцией масла. При нагрузке до 70% номинального тока циркуляция воздуха также естественная. При нагрузке 70% потери короткого замыкания в процентах номинальных потерь короткого замыкания составляют ![]() . Охлаждение осуществляется радиаторами, присоединенными к стенке бака. Вентиляторы размещены под радиаторами. Необходимо определить напор, возникающий в контуре циркуляции масла.
. Охлаждение осуществляется радиаторами, присоединенными к стенке бака. Вентиляторы размещены под радиаторами. Необходимо определить напор, возникающий в контуре циркуляции масла.
По данным чертежей 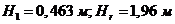 . По результатам измерений при нагрузке 70% и естественном охлаждении получены следующие данные:
. По результатам измерений при нагрузке 70% и естественном охлаждении получены следующие данные: 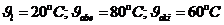 . На рис. 3-2 приведены диаграммы распределения температуры и удельного веса в контуре циркуляции, которые позволяют найти гравитационное давление, поддерживающее циркуляцию масла. Из данных измерений находим:
. На рис. 3-2 приведены диаграммы распределения температуры и удельного веса в контуре циркуляции, которые позволяют найти гравитационное давление, поддерживающее циркуляцию масла. Из данных измерений находим:
![]()
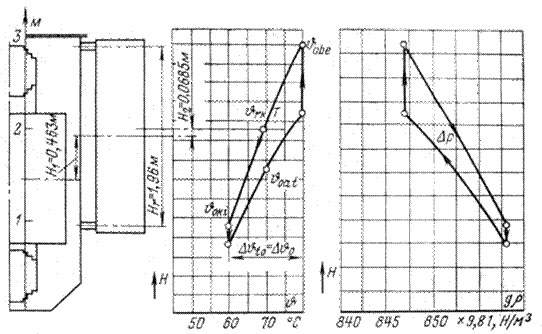
Рис. 3-2. К. определению гравитационного давления, поддерживающего циркуляцию масла, в трансформаторе мощностью 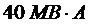 с естественным масляным охлаждением.
с естественным масляным охлаждением.
Определяем логарифмическую разность температур по формуле (3-6):
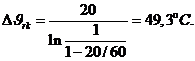
Определяем расстояние ![]() необходимое для построения диаграммы распределения температур, по формуле (3-11):
необходимое для построения диаграммы распределения температур, по формуле (3-11):
![]()
Определяем площадь температурной петли по формуле (3-12):
![]()
При ![]() и искомое гравитационное давление
и искомое гравитационное давление
![]()
Контур циркуляции масла
Контур циркуляции масла с точки зрения происходящих в нем тепловых процессов можно разделить на три характерных участка (см. рис. 3-1,а):
1) участок нагревания А–В;
2) приближенно изотермические участки В-С и В-A;
3) участок охлаждения С-D.
На участке А–В тепло от обмотки передается маслу. Холодное масло через каналы нижней изоляции входит в обмотку, соприкасается с поверхностью обмотки, имеющей более высокую, чем масло, температуру на размер перепада температуры ![]() , нагревается, снижает свой удельный вес и перемещается вверх. Пути движения масла по обмотке определяются вертикальными и горизонтальными масляными каналами, образованными рейками и прокладками. Соответствующим расположением вертикальных масляных каналов можно обеспечить имеющее определенное направление движения масла и в горизонтальных каналах между катушками. Выше было показано, что движение масла в обмотке носит пограничный характер.
, нагревается, снижает свой удельный вес и перемещается вверх. Пути движения масла по обмотке определяются вертикальными и горизонтальными масляными каналами, образованными рейками и прокладками. Соответствующим расположением вертикальных масляных каналов можно обеспечить имеющее определенное направление движения масла и в горизонтальных каналах между катушками. Выше было показано, что движение масла в обмотке носит пограничный характер.
Определенная часть нагретого масла охлаждается у стенки бака. Движением масла поэтому параллельному контуру в дальнейшем пренебрегаем, так как размер отводимых здесь потерь составляет всего несколько процентов от потерь, отдаваемых охлаждающей среде через радиаторы. Этот параллельный контур показан на рис. 3-3.
a) Горизонтальные каналы обмоток имеют четыре особенности:
b) катушки, образующие горизонтальные каналы, имеют вдоль канала практически постоянную на единице радиального размера поверхностную плотность теплового потока и равномерно подогревают движущееся вдоль канала масло;
c) температура находящихся в масле и расположенных друг над другом катушек тем больше, чем выше расположена катушка, а температура их поверхности выше температуры окружающего масла на размер перепада температуры ![]() ;
;
d) средняя температура пограничного слоя масла у поверхности катушки ![]() больше температуры масла, циркулирующего в каналах, на
больше температуры масла, циркулирующего в каналах, на 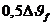 . Поскольку массовый расход масла в пограничном слое потока масла, движущегося в каналах внутри обмотки, большой, средняя температура этого слоя оказывает существенное влияние на температуру всего циркулирующего в каналах потока масла;
. Поскольку массовый расход масла в пограничном слое потока масла, движущегося в каналах внутри обмотки, большой, средняя температура этого слоя оказывает существенное влияние на температуру всего циркулирующего в каналах потока масла;
e) хотя движение масла носит пограничный характер, но благодаря расчлененности масляных каналов и частому изменению направления движения распределение температуры масла у выхода из обмотки в точке В можно считать близким к равномерному.
Масло, движущееся в вертикальных каналах стержня магнитопровода, подогревается с двух сторон. Хотя выделение тепла в стержне со стороны торцевых и со стороны боковых поверхностей листов не одинаковое, все же благодаря хорошей теплопроводности листов стали температуру стенок вертикальных охлаждающих каналов стержня можно принять постоянной. Циркуляция и в этих каналах носит пограничный характер.

Рис. 3-3. Основной и параллельный контуры циркуляции масла в трансформаторе с естественным масляным охлаждением.
Потери Р, передаваемые через поверхность теплоотдачи площадью ![]() при поверхностной плотности теплового потока q, повышают температуру циркулирующего масла, имеющего массовый расход Go и среднюю удельную теплоемкость с0, на
при поверхностной плотности теплового потока q, повышают температуру циркулирующего масла, имеющего массовый расход Go и среднюю удельную теплоемкость с0, на ![]() .
.
![]() .(3-14)
.(3-14)
Величину ![]() обозначим через
обозначим через ![]() . Тогда
. Тогда
![]() (3-15)
(3-15)
С учетом формул (3-7), (3-8) и (3-13) действующий при гравитационном механизме циркуляции масла напор ![]() определяется выражением
определяется выражением
![]() (3-16)
(3-16)
Пусть ![]() . Тогда
. Тогда
![]() .(3-17)
.(3-17)
Если в это уравнение подставить значение ![]() из формулы (3-15) и принять, что
из формулы (3-15) и принять, что ![]() то получим:
то получим:
![]() (3-18)
(3-18)
Это гравитационное давление покрывает потери давления, возникающие при движении масла и обусловленные гидравлическими сопротивлениями в контуре циркуляции масла. Если режим движения ламинарный, то возникающие при циркуляции потери давления пропорциональны массовому расходу масла:
![]() (3-19)
(3-19)
Приравнивая два последних выражения для ![]() получаем, что
получаем, что
![]() (3-20)
(3-20)
где ![]()
Подставляя в формулу (3-15) значение Go по формуле (3-20), определяем осевой перепад температуры масла в обмотке:
![]() , (3-21)
, (3-21)
где ![]() .
.
Тогда по формуле (3-17)
![]() ,(3-22)
,(3-22)
где ![]() .
.
Существование этих зависимостей подтверждено экспериментально. На рис. приведены семейства различных кривых, построенных по данным экспериментов. Первое семейство представляет собой зависимость ![]() (рис. 3-4). Измерения были проведены на моделях обмотки. Для изменения гидравлического сопротивления контура циркуляции в модель была встроена регулировочная задвижка. Степень закрытия задвижки регулировалась числом оборотов рукоятки:
(рис. 3-4). Измерения были проведены на моделях обмотки. Для изменения гидравлического сопротивления контура циркуляции в модель была встроена регулировочная задвижка. Степень закрытия задвижки регулировалась числом оборотов рукоятки: ![]() Последнее число соответствовало полному открытию задвижки.
Последнее число соответствовало полному открытию задвижки.
На рис. 3-5 и 3-6 приведены зависимости ![]() и
и 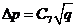 , построенные для различных значений гидравлического сопротивления контура циркуляции.
, построенные для различных значений гидравлического сопротивления контура циркуляции.
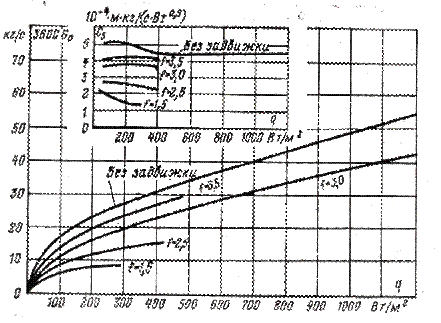
Рис. 3-4. Зависимость  полученная экспериментальным путем.
полученная экспериментальным путем.

Рис. 3-5. Зависимость  , полученная экспериментальным путем.
, полученная экспериментальным путем.
Из дополнительных кривых, приведенных на рис. , видно, что при открытой задвижке и значениях q около 1000 Вт/м2 коэффициенты С5, С6 и С7 могут быть приняты постоянными.
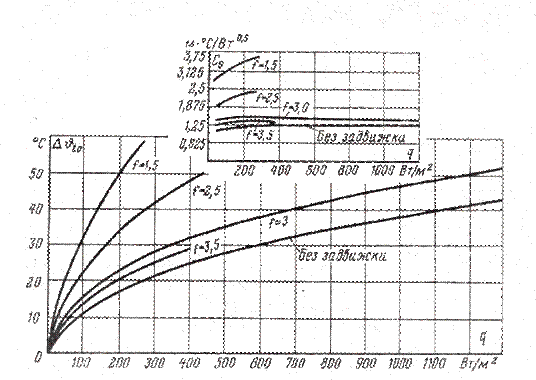
Рис. 3-6. Зависимость  , полученная экспериментальным путем.
, полученная экспериментальным путем.
Измерения были проведены для трех моделей обмоток (рис. 3-7), имеющих следующие размеры:
Обозначение точек измерения | Размеры модели, мм | ||
s | b |
| |
O | 20 | 50 | 15 |
+ | 4 | 40 | 5 |
D | 10 | 30 | 10 |
На рис. 3-8 показано изменение площади петли давления в зависимости от поверхностной плотности теплового потока q для модели обмотки с размерами: ![]() . Кривые построены для следующих семи значений q: 73,8; 163; 227; 377; 638; 1020; 1245 Вт/м2.
. Кривые построены для следующих семи значений q: 73,8; 163; 227; 377; 638; 1020; 1245 Вт/м2.
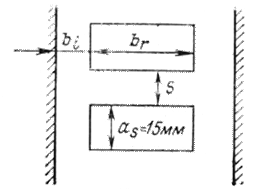
Рис. 3-7. Размеры модели обмотки, используемой при эксперимнтах.
На рис. 3-9 для той же модели обмотки показано изменение площади петли давления в зависимости от положения задвижки при ![]() . Из диаграммы видно, что увеличение гидравлического сопротивления контура циркуляции приводит к увеличению площади петли и перепада температуры
. Из диаграммы видно, что увеличение гидравлического сопротивления контура циркуляции приводит к увеличению площади петли и перепада температуры ![]() .
.
Последнее семейство диаграмм распределения удельного веса масла ясно показывает, что увеличение гидравлического сопротивления контура циркуляции, в первую очередь гидравлического сопротивления радиаторов, существенно влияет на перепад температуры ![]() . Добиться значительного уменьшения гидравлического сопротивления обмотки нельзя однако при ошибке в конструкции (при очень малых каналах в обмотке или в концевой изоляции, через которую поступает масло) сопротивление обмотки может оказаться большим. При хорошей конструкции гидравлическое сопротивление обмотки так мало, что им по сравнению с остальным сопротивлением контура можно пренебречь.
. Добиться значительного уменьшения гидравлического сопротивления обмотки нельзя однако при ошибке в конструкции (при очень малых каналах в обмотке или в концевой изоляции, через которую поступает масло) сопротивление обмотки может оказаться большим. При хорошей конструкции гидравлическое сопротивление обмотки так мало, что им по сравнению с остальным сопротивлением контура можно пренебречь.
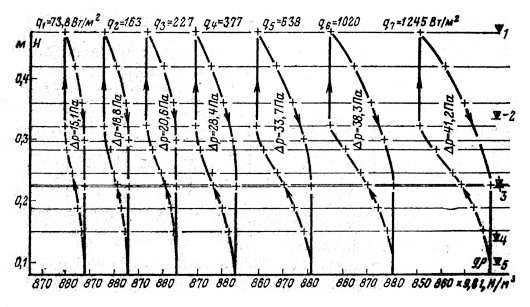
Рис. 3-8. Изменение площади петли давления в зависимости от поверхностной плотности теплового потока.
1 - уровень верхнего патрубка радиатора;2 - уровень верхнего края обмотки; 3- уровень нижнего патрубка радиатора; 4 - уровень нижнего края обмотки; 5 - уровень входа масла в бак.
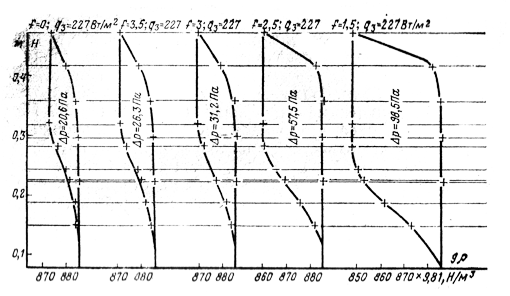
Рис. 3-9. Изменение площади петли давления от гидравлического сопротивления при постоянной поверхностной плотности теплового потока (высоты патрубков радиаторов и краев обмотки см. на рис. 3-8).
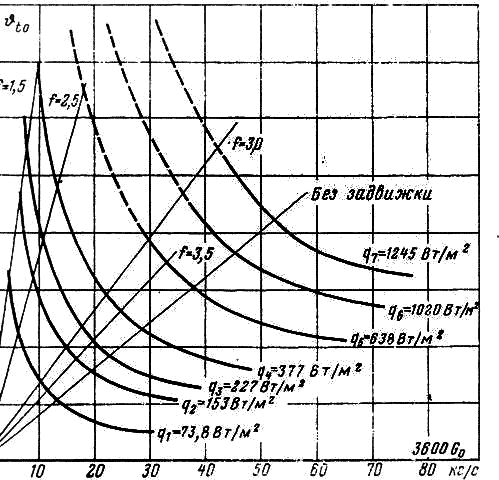
Рис. 3-10. Зависимость 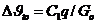 , полученная экспериментальным путем».
, полученная экспериментальным путем».
Возникающее гравитационное давление расходуется главным образом на преодоление сопротивления радиаторов.
На рис. 3-10 изображены кривые зависимости ![]() , полученные на основании экспериментов. Из этих кривых видно, что каждому положению задвижки f и значению поверхностной плотности теплового потока q соответствует одна рабочая точка. Рабочая точка является точкой пересечения кривых, построенных при
, полученные на основании экспериментов. Из этих кривых видно, что каждому положению задвижки f и значению поверхностной плотности теплового потока q соответствует одна рабочая точка. Рабочая точка является точкой пересечения кривых, построенных при ![]() и
и 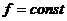 . Соответствующие этим точкам значения Go и
. Соответствующие этим точкам значения Go и ![]() однозначно определяют гравитационный процесс циркуляции масла.
однозначно определяют гравитационный процесс циркуляции масла.
3-2. Циркуляция масла в радиаторе и расчет перепада температуры между маслом и стенкой радиатора
Скорость масла в радиаторе при естественной циркуляции масла и воздуха
Прежде чем определить действительные картины распределения скорости движения и температуры масла, рассмотрим пример расчета.
Пример.
Задан радиатор высотой 2440 мм. Секция радиатора имеет семь масляных каналов, поперечное сечение которых представляет собой удвоенную трапецию (рис. 3-11). Площадь сечения каждого канала 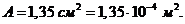 Полная площадь сечения всех каналов
Полная площадь сечения всех каналов
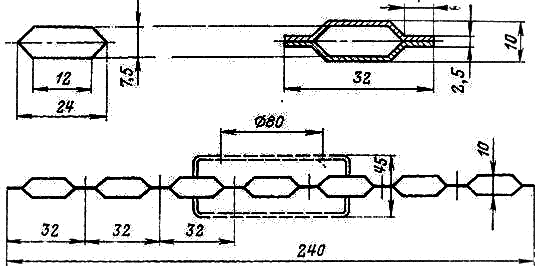
Рис. 3-11. Сечение секции радиатора (характеристики - см. табл. 3-1).
секции ![]() Смоченный периметр одного канала
Смоченный периметр одного канала ![]()
Гидравлический диаметр по формуле (2-28а) ![]() :
:
![]()
Площадь внутренней поверхности секции радиатора (со стороны масла) 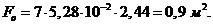
Площадь наружной поверхности секции (со стороны воздуха) ![]() . Пусть
. Пусть ![]() поверхностная плотность теплового потока со стороны воздуха при конвективном теплообмене
поверхностная плотность теплового потока со стороны воздуха при конвективном теплообмене ![]()
Потери, отводимые путем конвекции со стороны воздуха,
![]()
Такие же потери должны быть переданы и со стороны масла:
![]()
Отсюда видно, что поверхностная плотность теплового потока со стороны масла равна поверхностной плотности теплового потока со стороны воздуха, умноженной на отношение площадей наружной и внутренней поверхности радиатора.
Разность теплосодержаний масла на входе и выходе радиатора численно равна потерям, переданным со стороны масла стенкам радиатора и далее через них охлаждающему воздуху. Пусть 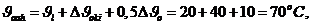 , плотность масла
, плотность масла 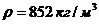 , удельная теплоемкость
, удельная теплоемкость ![]() . Обозначим скорость масла в радиаторах через
. Обозначим скорость масла в радиаторах через ![]() .
.
По уравнению теплового баланса находим:
![]()
Отсюда скорость масла
![]()
Крайние секции радиаторов с половины своей поверхности со стороны, обращенной к воздуху, отдают тепло охлаждающему воздуху также путем излучения, в результате чего увеличивается средняя плотность теплового потока. Если поверхностная плотность теплового потока при излучении ![]() , то средняя плотность теплового потока крайней секции увеличится на
, то средняя плотность теплового потока крайней секции увеличится на ![]() . В рассматриваемом примере наибольшее среднее значение плотности теплового потока равно
. В рассматриваемом примере наибольшее среднее значение плотности теплового потока равно 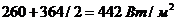 , т. е. на 70% больше, чем плотность теплового потока при только конвективном теплообмене. Поэтому скорость масла при неизменном перепаде температуры
, т. е. на 70% больше, чем плотность теплового потока при только конвективном теплообмене. Поэтому скорость масла при неизменном перепаде температуры ![]() увеличится в крайней секции до
увеличится в крайней секции до ![]() . Увеличение теплового потока крайней секции приводит к усилению циркуляции масла. Однако увеличение расхода масла в крайних секциях радиаторов практически не окажет влияния на значения
. Увеличение теплового потока крайней секции приводит к усилению циркуляции масла. Однако увеличение расхода масла в крайних секциях радиаторов практически не окажет влияния на значения ![]() и
и ![]() трансформатора в целом. Если между секциями радиаторов установить излучатели, то тепловой поток внутренней поверхности радиатора также увеличится на 40% по сравнению с тепловым потоком при только конвективном теплообмене. Это означает, что результирующая плотность теплового потока крайней секции увеличится еще на
трансформатора в целом. Если между секциями радиаторов установить излучатели, то тепловой поток внутренней поверхности радиатора также увеличится на 40% по сравнению с тепловым потоком при только конвективном теплообмене. Это означает, что результирующая плотность теплового потока крайней секции увеличится еще на 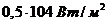 и достигнет значения
и достигнет значения ![]() , которое на 90% больше, чем плотность теплового потока при только конвективном теплообмене. Таким образом, возможное наибольшее значение скорости масла не превысит
, которое на 90% больше, чем плотность теплового потока при только конвективном теплообмене. Таким образом, возможное наибольшее значение скорости масла не превысит ![]() .
.
Из рассмотренного примера следует, что скорость циркуляции масла в радиаторах очень мала. Определим коэффициент теплоотдачи со стороны масла и перепад температуры между маслом и стенкой радиатора, исходя из условий конвективного теплообмена и соответствующей ему скорости масла ![]() .
.
Коэффициент теплоотдачи радиатора со стороны масла и перепад температуры между маслом и стенкой радиатора
Режим течения масла в масляных каналах радиатора - ламинарный. Как уже было показано, круговое движение масла поддерживается той разностью давлений, которая возникает в связи с изменением удельного веса благодаря теплообмену между частицами масла и равна площади петли давления на диаграмме распределения удельных весов. В этом случае движение масла можно рассматривать как принудительное движение и поэтому можно воспользоваться известным по [9] критериальным уравнением
![]() (3-23)
(3-23)
С помощью этого уравнения можно определить коэффициент теплоотдачи радиатора со стороны масла. В это уравнение необходимо подставлять физические характеристики масла, соответствующие средней температуре пограничного слоя масла.
Предположим, что перепад температуры между маслом и стенкой ![]() . В этом случае средняя температура пограничного слоя масла
. В этом случае средняя температура пограничного слоя масла
![]() .
.
Соответствующие этой температуре физические характеристики масла находим по табл. 1-1: 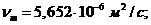
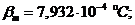
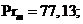
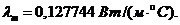 Скорость масла
Скорость масла 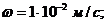 гидравлический диаметр
гидравлический диаметр ![]() .
.

|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 |




