При ![]() =200С число Re =4070
=200С число Re =4070![]() и критическое значение числа
и критическое значение числа 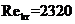 достигается уже при скорости воздуха
достигается уже при скорости воздуха ![]() м/с. Зависимости числа Re от скорости воздуха при разных значениях
м/с. Зависимости числа Re от скорости воздуха при разных значениях ![]() приведены на рис. 3-22. Из этого рисунка видно, что при практически встречающихся значениях температуры воздуха и значениях
приведены на рис. 3-22. Из этого рисунка видно, что при практически встречающихся значениях температуры воздуха и значениях ![]() м/с течение воздуха имеет турбулентный характер. Этот вывод был получен и при рассмотрении критической высоты радиаторов.
м/с течение воздуха имеет турбулентный характер. Этот вывод был получен и при рассмотрении критической высоты радиаторов.

Рис. 3-22. Зависимости числа Re от скорости воздуха w при разных значениях температуры воздуха![]()
Коэффициент теплоотдачи радиатора со стороны воздуха при высоте радиаторов больше критической
Формулы для расчета коэффициента теплоотдачи, относящиеся к ламинарному или турбулентному режиму.
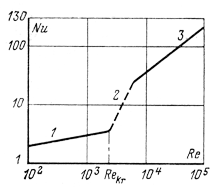
Рис. 3-23. Зависимость числа Nu от числа Re в переходной области между ламинарным течением среды GrPr–I по данным на [9].
1 – ламинарный режим; 2 – переходная область 3 - турбулентный режим
течения, для переходной области, где число ![]() , не справедливы. Можно было бы для определения числа Nu воспользоваться результатами исследований [9] по рис. 3-23, однако эти данные получены не для радиаторов. Поэтому для расчета коэффициента теплоотдачи воспользуемся в целях осторожности уравнением (3-23), относящимся к ламинарному режиму течения:
, не справедливы. Можно было бы для определения числа Nu воспользоваться результатами исследований [9] по рис. 3-23, однако эти данные получены не для радиаторов. Поэтому для расчета коэффициента теплоотдачи воспользуемся в целях осторожности уравнением (3-23), относящимся к ламинарному режиму течения:
![]()
Однако необходимо помнить, что коэффициент теплоотдачи будет фактически больше и приближаться к значению, определенному исходя из уравнения, справедливого для турбулентного режима течения:
![]() (3-52)
(3-52)
где индекс f указывает на то, что в длимое уравнение необходимо подставлять физические характеристики воздуха, определенные при его средней температуре.
Потери давления на трение в радиаторах со стороны воздуха
Для расчета потери давления на трение ![]() также используются две формулы. При ламинарном режиме течения
также используются две формулы. При ламинарном режиме течения
![]() (3-53)
(3-53)
при турбулентном режиме течения
![]() (3-54)
(3-54)
Для того чтобы создать определенный запас, расчеты целесообразнее выполнять по формуле, относящейся к турбулентному режиму.
Подставим в формулу для ламинарного режима выражение для числа Re. Тогда
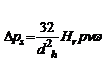 (3-53а)
(3-53а)
Учитывая, что dh=6,4* 10-2 м, и произведя соответствующие вычисления, получаем:
![]() (3-53б)
(3-53б)
После аналогичных преобразований формулы для турбулентного режима примут вид:
![]() (3-54а)
(3-54а)
и
![]() (3-54б)
(3-54б)
Теплоотдача радиаторов при естественной циркуляции масла и воздуха
Расчет теплоотдачи радиаторов, имеющих высоту, превышающую критическую, выполняется как для теплообменника с противотоком.
При заданных значениях высоты радиатора, теплового потока и температуры воздуха у входа в радиатор средняя скорость и осевой перепад температуры воздуха определяются исходя из уравнения теплового баланса и уравнения Эйлера. Для какого-то выбранного среднего перепада температуры между стенкой радиатора и воздухом определяется средняя температура пограничного слоя и соответствующий ей коэффициент теплоотдачи. Если средний перепад температуры выбран правильно, то произведение коэффициента теплоотдачи, среднего перепада температуры и поверхности теплоотдачи определяет тепловой поток радиатора. Тепловой поток целесообразно представлять именно в виде зависимости от среднего перепада температуры между стенкой радиатора и воздухом. В качестве не изменяющегося параметра выбрана температура охлаждающего воздуха.
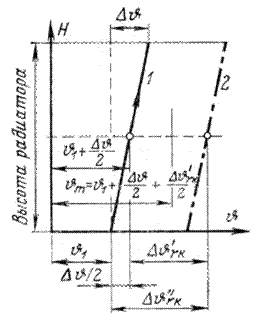
Рис. 3-24. К расчету теплоотдачи радиатора. 1 - температура нагревающегося воздуха; 2 - температура стенки радиатора.
Целесообразность выбора в качестве независимой переменной среднего перепада температуры между стенкой радиатора и воздухом заключается в том, что он определяет размеры системы охлаждения и может быть легко найден при тепловом расчете обмотки путем вычитания из нормированного значения превышения средней температуры обмотки над температурой воздуха, равного 650С, значения ![]() и значения перепада температуры между маслом и стенкой радиатора.
и значения перепада температуры между маслом и стенкой радиатора.
Произведем расчет зависимости теплового потока радиатора от перепада температуры между стенкой радиатора и воздухом.
Введем следующие обозначения (рис. 3-24):
![]() – температура воздуха у входа в радиатор;
– температура воздуха у входа в радиатор;
![]() – осевой перепад температуры воздуха в радиаторе;
– осевой перепад температуры воздуха в радиаторе;
![]() – средняя температура воздуха в радиаторе;
– средняя температура воздуха в радиаторе;
![]() – превышение средней температуры стенки радиатора над средней температурой циркулирующего в радиаторе воздуха;
– превышение средней температуры стенки радиатора над средней температурой циркулирующего в радиаторе воздуха;
![]() – превышение средней температуры стенки радиатора над температурой воздуха у входа в радиатор;
– превышение средней температуры стенки радиатора над температурой воздуха у входа в радиатор;
![]() – средняя температура пограничного слоя воздуха;
– средняя температура пограничного слоя воздуха;
![]() – разность давлении в радиаторе со стороны воздуха, которая определяется разностью плотностей холодного и нагретого воздуха;
– разность давлении в радиаторе со стороны воздуха, которая определяется разностью плотностей холодного и нагретого воздуха;
– высота радиатора (диаграммы теплового потока строятся для пяти значений высоты: (![]() );
);
![]() – нормальное ускорение свободного падения;
– нормальное ускорение свободного падения;
dh – гидравлический диаметр (для рассматриваемых радиаторов db=6,4*10-2 м);
![]() площадь поперечного сечения канала для потока воздуха между двумя секциями (для рассматриваемых радиаторов
площадь поперечного сечения канала для потока воздуха между двумя секциями (для рассматриваемых радиаторов 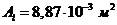 );
);
![]() площадь поверхности теплоотдачи со стороны воздуха для одной секции (для пяти рассматриваемых радиаторов различной высоты:
площадь поверхности теплоотдачи со стороны воздуха для одной секции (для пяти рассматриваемых радиаторов различной высоты: 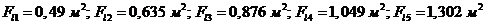 );
);
Р – тепловой поток секции радиатора при конвективном теплообмене;
![]() – скорость воздуха у входа в радиатор
– скорость воздуха у входа в радиатор
![]() – скорость воздуха у выхода из радиатора;
– скорость воздуха у выхода из радиатора;
![]() – средняя скорость воздуха в радиаторе;
– средняя скорость воздуха в радиаторе;
![]() – коэффициент теплоотдачи радиатора со стороны воздуха;
– коэффициент теплоотдачи радиатора со стороны воздуха;
![]() – плотность воздуха у входа в радиатор при температуре
– плотность воздуха у входа в радиатор при температуре ![]()
![]() – плотность воздуха у выхода из радиатора при температуре
– плотность воздуха у выхода из радиатора при температуре ![]() ;
;
![]() – средняя плотность воздуха в радиаторе;
– средняя плотность воздуха в радиаторе;
![]() – удельная теплоемкость воздуха при средней температуре воздуха в радиаторе, равной
– удельная теплоемкость воздуха при средней температуре воздуха в радиаторе, равной ![]()
![]() – коэффициент кинематической вязкости воздуха при средней температуре воздуха в радиаторе, равной
– коэффициент кинематической вязкости воздуха при средней температуре воздуха в радиаторе, равной![]() ;
;
![]() – температура воздуха у выхода из радиатора;
– температура воздуха у выхода из радиатора;
![]() –термодинамическая температура воздуха у входа в радиатор, К;
–термодинамическая температура воздуха у входа в радиатор, К;
![]() – термодинамическая температура воздуха у выхода из радиатора, К.
– термодинамическая температура воздуха у выхода из радиатора, К.
Необходимо найти систему из двух уравнений для расчета осевого перепада температуры воздуха ЛФ и скорости![]() . Разность давлений, обусловленная разностью удельных весов воздуха, равна сумме местных потерь давления на выходе из радиатора и потерь давления на трение. Потери давления на входе в радиатор очень маленькие и поэтому не учитываются:
. Разность давлений, обусловленная разностью удельных весов воздуха, равна сумме местных потерь давления на выходе из радиатора и потерь давления на трение. Потери давления на входе в радиатор очень маленькие и поэтому не учитываются:
![]() (3-55)
(3-55)
Тепловой поток радиатора полностью расходуется на подогрев воздуха:
![]() (3-56)
(3-56)
Выразим все средние величины и величины у выхода из радиатора через величины у входа в радиатор. При этом учитываем два вытекающих из физических законов положения: плотность воздуха обратно пропорциональна термодинамической температуре, т. е.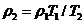 ; массовый расход воздуха в любом поперечном сечении канала между секциями радиатора остается постоянным, т. е.
; массовый расход воздуха в любом поперечном сечении канала между секциями радиатора остается постоянным, т. е.
![]() (3-57)
(3-57)
![]() (3-58)
(3-58)
![]() Тогда
Тогда
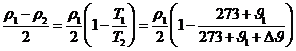 (3-59)
(3-59)
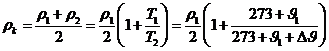 (3-60)
(3-60)
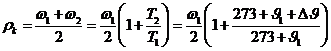 (3-61)
(3-61)
При нормальном атмосферном давлении и температуре ![]() плотность сухого воздуха, кг/м3:
плотность сухого воздуха, кг/м3:
![]() (3-62)
(3-62)
Удельная теплоемкость воздуха, Дж/(кг 0С) при температуре ![]() :
:
![]() (3-63)
(3-63)
Коэффициент кинематической вязкости воздуха, м2/с, при температуре ![]() :
:
![]() (3-64)
(3-64)
Пример 3-4. Для заданных значений ![]() и
и ![]() определим соответствующие друг другу значения
определим соответствующие друг другу значения ![]() и
и ![]() , которые будут справедливыми при разных значениях Р.
, которые будут справедливыми при разных значениях Р.
Если ![]() м;
м; ![]() 0C;
0C; ![]() Вт, то можно записать в численном виде уравнения (3-55) и (3-56), используя выражения (3-59) –(3-64):
Вт, то можно записать в численном виде уравнения (3-55) и (3-56), используя выражения (3-59) –(3-64):
![]()
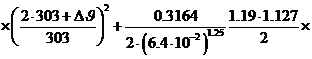
![]()
![]()
![]()
![]()
эти два уравнения позволяют определить при заданных значениях ![]() , Н и Р соответствующие друг другу значения
, Н и Р соответствующие друг другу значения ![]() и
и ![]()
б) Запишем уравнение теплоотдачи для стороны воздуха
![]() (3-65)
(3-65)
и подставим в него выражение для коэффициента теплоотдачи, соответствующее ламинарному режиму согласно уравнению (3-23).
Тогда тепловой поток
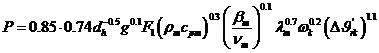
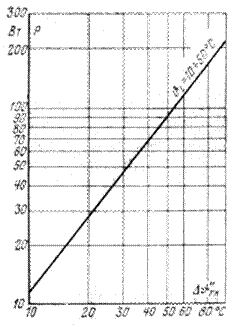
Рис. 3-25. Теплоотдача радиатора с 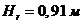 при естественной циркуляции воздуха.
при естественной циркуляции воздуха.
Физические параметры воздуха, зависящие от температуры, необходимо определить при средней температуре пограничного слоя ![]() . Дальнейший ход расчета по полученному уравнению (3-66) следующий: подставим в уравнение заданное значение Р, соответствующее ему значение
. Дальнейший ход расчета по полученному уравнению (3-66) следующий: подставим в уравнение заданное значение Р, соответствующее ему значение ![]() и значения не за: висящих от температуры пара: метров;
и значения не за: висящих от температуры пара: метров;
выберем некоторое значение ![]()
определим через ![]() ,
, ![]() и
и ![]() значение средней температуры пограничного слоя
значение средней температуры пограничного слоя ![]() ;
;
подставим в уравнение значения физических параметров при средней температуре пограничного слоя ![]()
определим из уравнения при заданном значении Р значение ![]()
Если определенное таким образом значение ![]() равно выбранному значению
равно выбранному значению ![]() , то расчет закончен; если это не выполняется, то снова задаются другим значением
, то расчет закончен; если это не выполняется, то снова задаются другим значением ![]() и проводят расчет в указанной выше последовательности. Дальнейшие вычисления заключаются в представлении Р в виде функции от
и проводят расчет в указанной выше последовательности. Дальнейшие вычисления заключаются в представлении Р в виде функции от ![]() .
.
С помощью полученной выше системы уравнений было найдено, что ![]() м/с при Р=200 Вт и
м/с при Р=200 Вт и ![]() 0С. Пусть
0С. Пусть ![]() 0С. Тогда
0С. Тогда
![]() 0С.
0С.
Одна секция радиатора с 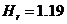 м имеет поверхность теплоотдачи
м имеет поверхность теплоотдачи ![]() м2. С учетом полученных данных можно записать уравнение (3-66) в численном выражении:
м2. С учетом полученных данных можно записать уравнение (3-66) в численном выражении:
![]()
![]()
Если численное значение правой части равенства будет равно 200, то значение ![]() было выбрано правильно. Предположим, что это так.
было выбрано правильно. Предположим, что это так.

Рис. 3-26. Теплоотдача радиатора с 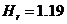 м при естественной циркуляции воздуха.
м при естественной циркуляции воздуха.
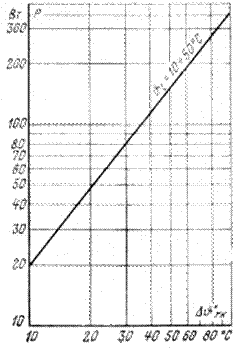
Рис. 3-27. Теплоотдача радиатора с 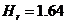 м при естественной циркуляции воздуха.
м при естественной циркуляции воздуха.

Рис. 3-28. Теплоотдача радиатора с 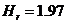 м при естественной циркуляции воздуха.
м при естественной циркуляции воздуха.
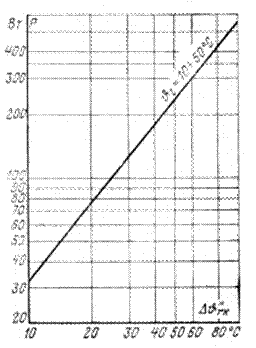
Рис. 3-29. Теплоотдача радиатора с  м при естественной циркуляции воздуха.
м при естественной циркуляции воздуха.
это так. Тогда сразу находим обе искомые величины:
![]()
и соответствующий тепловой поток Р=200 Вт.
Результаты, полученные на основании расчетов на вычислительной машине по описанному здесь способу для диапазона температур воздуха ![]() , приведены на рис. .
, приведены на рис. .
Коэффициент полезного действия ребер
Каждая секция радиатора по рис. 3-13 имеет семь трубчатых каналов для прохождения масла. К каждому трубчатому каналу согласно рис. 3-11 относятся два ребра. Необходимо определить КПД одного ребра. Согласно рис. 3-11 толщина ребра ![]() м и длина ребра
м и длина ребра ![]() м. Материал радиатора - холоднокатаный стальной лист, имеющий коэффициент теплопроводности
м. Материал радиатора - холоднокатаный стальной лист, имеющий коэффициент теплопроводности
![]()
Коэффициент полезного действия ребра
![]() (3-67)
(3-67)
где
![]() ; (3-37 a)
; (3-37 a)
![]() – коэффициент теплоотдачи ребра со стороны воздуха.
– коэффициент теплоотдачи ребра со стороны воздуха.
При подстановке в формулу (3-67а) данных для ребра находим:
![]() ,
,
![]()
Пример 3-5. Пусть 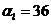 Вт/(м2 0С). Для такого значения величина
Вт/(м2 0С). Для такого значения величина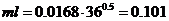 .
.
Коэффициент полезного действия ребра по формуле (3-67)
![]() .
.
Даже при относительно больших значениях ![]() КПД ребра близок к единице. Это означает, что увеличение поверхности с помощью ребер очень эффективно и что нет необходимости учитывать при расчете поверхность ребра раздельно от остальной части поверхности.
КПД ребра близок к единице. Это означает, что увеличение поверхности с помощью ребер очень эффективно и что нет необходимости учитывать при расчете поверхность ребра раздельно от остальной части поверхности.
Коэффициент теплопередачи радиатора
Введем следующие обозначения: ![]() и
и ![]() – площади поверхностей секции радиатора со стороны воздуха и масла соответственно;
– площади поверхностей секции радиатора со стороны воздуха и масла соответственно;
![]() – площадь поверхности "секции радиатора, соответствующая средней по толщине стенки поверхности трубчатого канала;
– площадь поверхности "секции радиатора, соответствующая средней по толщине стенки поверхности трубчатого канала;
![]() и
и ![]() – коэффициенты теплоотдачи радиатора со стороны воздуха и масла соответственно;
– коэффициенты теплоотдачи радиатора со стороны воздуха и масла соответственно;
![]() – коэффициент теплопроводности материала радиатора;
– коэффициент теплопроводности материала радиатора;
![]() –толщина стенки радиатора.
–толщина стенки радиатора.
Коэффициент теплопередачи при конвекции ![]() , отнесенный к площади поверхности секции радиатора со стороны воздуха, определяется из уравнения
, отнесенный к площади поверхности секции радиатора со стороны воздуха, определяется из уравнения
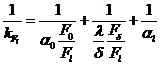 (3-68)
(3-68)
Радиаторы по рис. 3-13 отличаются друг от друга только высотой ![]() . Для каждого радиатора:
. Для каждого радиатора:
![]()
![]()
По данным рис. 3-13: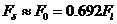 ; и
; и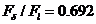 .
.
Толщина стенки радиатора 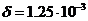 м, коэффициент теплопроводности
м, коэффициент теплопроводности ![]() Вт/(м 0С). С учетом этих данных
Вт/(м 0С). С учетом этих данных
![]()
![]()
Таким образом, вторым членом в уравнении (3-68) можно пренебречь и это уравнение для радиаторов по рис. 3-13 примет вид:
![]() (3-86а)
(3-86а)
Обозначим потери, отводимые одной секцией радиатора путем конвекции, через Р. Тогда превышение средней температуры масла в радиаторе над средней температурой воздуха в радиаторе, являющееся логарифмической разностью температур, определяется выражением
![]() (3-69)
(3-69)
где ![]() – поверхностная Плотность теплового потока, отнесенная к площади поверхности секции радиатора со стороны воздуха.
– поверхностная Плотность теплового потока, отнесенная к площади поверхности секции радиатора со стороны воздуха.
Это превышение температуры состоит из двух слагаемых:
перепада температуры между маслом и стенкой радиатора
![]() (3-70)
(3-70)
перепада температуры между стенкой радиатора и воздухом
![]() (3-71)
(3-71)
Соответственно
![]() (3-72)
(3-72)
3-6. Теплопередача радиаторов при принудительной циркуляции воздуха
Коэффициент теплоотдачи со стороны воздуха
Коэффициент теплоотдачи при принудительной циркуляции воздуха может быть найден из критериального уравнения [см. также уравнение (3-52)]:
![]() (3-73)
(3-73)
которое описывает турбулентный режим течения жидкости или газа (например, воздуха) в каналах. Индекс ![]() указывает на то, что в данное уравнение необходимо подставлять физические характеристики воздуха, определенные при его средней температуре;
указывает на то, что в данное уравнение необходимо подставлять физические характеристики воздуха, определенные при его средней температуре; ![]() – поправочный коэффициент, который зависит от отношения длины канала к его гидравлическому диаметру числа Re. Значения коэффициента
– поправочный коэффициент, который зависит от отношения длины канала к его гидравлическому диаметру числа Re. Значения коэффициента ![]() приведены в табл. 3-11.
приведены в табл. 3-11.
Таблица 3-11
Зависимость коэффициента ![]() от отношения высоты радиатора к гидравлическому диаметру
от отношения высоты радиатора к гидравлическому диаметру![]() для
для ![]()
| 1 | 2 | 5 | 10 | 15 | 20 | 30 | 40 | 50 |
| 1,65 | 1,50 | 1,34 | 1,23 | 1,17 | 1,13 | 1,07 | 1,03 | 1,00 |
При работе вентиляторов скорость воздуха в радиаторе обычно всегда больше 1 м/с, а размер гидравлического диаметра канала таков, что число ![]() в вероятном диапазоне температур воздуха больше 2200. Поэтому движение воздуха в радиаторе будет иметь турбулентный характер.
в вероятном диапазоне температур воздуха больше 2200. Поэтому движение воздуха в радиаторе будет иметь турбулентный характер.
Формула для определения коэффициента теплоотдачи радиатора со стороны воздуха, полученная из критериального уравнения (3-73):
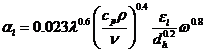 (3-74)
(3-74)
Гидравлический диаметр
При обдуве радиатора снизу гидравлический диаметр равен гидравлическому диаметру плоского канала, образованного соседними секциями и боковыми щитами.
При обдуве сбоку гидравлический диаметр равен четырехкратной длине пути воздушного потока L, умноженной на отношение площади свободного для прохождения потока воздуха поперечного сечения ![]() к относящейся к нему площади поверхности теплоотдачи
к относящейся к нему площади поверхности теплоотдачи ![]() .
.
![]() (3-75)
(3-75)
Если друг за другом размещены несколько радиаторов, то соответственно длина и площадь теплоотдачи умножаются на число последовательно размещенных радиаторов.
Радиаторы с принудительной циркуляцией воздуха как масляно-воздушные охладители
Циркуляция масла может быть естественной, т. е. обусловленной гравитационными силами, или принудительной, т. е. создаваемой насосом. При постоянных потерях с увеличением скорости воздуха, т. е. с увеличением коэффициента теплоотдачи со стороны воздуха, превышение средней температуры масла в радиаторе над температурой воздуха сначала быстро, а потом все медленнее уменьшается, стремясь к предельному минимальному значению, соответствующему тому возросшему значению коэффициента теплопередачи, который может быть достигнут при данном коэффициенте теплоотдачи со стороны масла. Одновременно со снижением превышения средней температуры масла возрастает площадь, охваченная петлей давления, которая изображается в виде функции![]() , в результате чего увеличивается обусловливающий циркуляцию масла напор или подъемная сила. Увеличение напора связано также с тем, что, с одной стороны, увеличивается разность высот центров охлаждения и нагрева из-за смещения вверх центра охлаждения в результате улучшения охлаждения радиатора и, с другой стороны, увеличивается зависящий от самопроизвольно устанавливающейся скорости масла осевой перепад температуры масла в обмотке из-за увеличения вязкости масла при его более низкой средней температуре. Увеличенный движущий напор покрывает возрастающее гидравлическое сопротивление контура при циркуляции масла с увеличенной скоростью.
, в результате чего увеличивается обусловливающий циркуляцию масла напор или подъемная сила. Увеличение напора связано также с тем, что, с одной стороны, увеличивается разность высот центров охлаждения и нагрева из-за смещения вверх центра охлаждения в результате улучшения охлаждения радиатора и, с другой стороны, увеличивается зависящий от самопроизвольно устанавливающейся скорости масла осевой перепад температуры масла в обмотке из-за увеличения вязкости масла при его более низкой средней температуре. Увеличенный движущий напор покрывает возрастающее гидравлическое сопротивление контура при циркуляции масла с увеличенной скоростью.
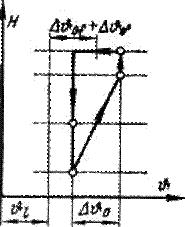
Рис. 3-30. Диаграмма распределения температуры масла в контуре циркуляции при потерях Р и бесконечно большом коэффициенте теплоотдачи со стороны воздуха.
При очень большой скорости воздуха, т. е. при очень большом коэффициенте теплоотдачи со стороны воздуха, масло успевает охладиться в самой верхней части радиатора (рис. 3-30). В таком предельном случае большая часть радиатора служит только в качестве маслопровода и для отвода тепла достаточна очень малая поверхность. Осевой перепад температуры масла в обмотке устанавливается самопроизвольно. Площадь петли давления станет такой, чтобы покрыть потери давления, возникающие при циркуляции масла.

Рис. 3-31. Диаграмма распределения температуры масла в контуре циркуляции при потерях Р'^Р и бесконечно большом коэффициенте теплоотдачи со стороны воздуха.
Теперь целесообразно рассмотреть случай, когда наряду с увеличением коэффициента теплоотдачи со стороны воздуха увеличиваются также потери таким образом, чтобы превышение средней температуры масла в радиаторе над температурой воздуха оставалось неизменным. С увеличением потерь увеличивается осевой перепад температуры масла в обмотке. С одной стороны, из-за этого возрастет площадь петли давления, а с другой – произойдет смещение центра нагрева вверх. Скорость циркуляции масла все же возрастет, и увеличение площади петли давления компенсирует возросшие потери давления в контуре циркуляции. Вязкость масла практически не изменится, поскольку средняя температура масла в радиаторе поддерживается неизменной. Увеличение потерь ограничивается существованием верхней теоретической границы. Если предположить, что коэффициент теплоотдачи со стороны воздуха равен бесконечности, то средняя температура масла в радиаторе будет равна сумме трех величин: температуры охлаждающего воздуха ![]() , перепада температуры по толщине стенки
, перепада температуры по толщине стенки ![]() и перепада температуры между маслом и стенкой радиатора
и перепада температуры между маслом и стенкой радиатора ![]() (см. рис. 3-31, а также 3-30). В этом случае, как и в предшествующем, радиатор тоже играет только роль маслопровода, поскольку при бесконечно большом коэффициенте теплоотдачи дли отвода тепла достаточно иметь очень малую поверхность у верхней части радиатора.
(см. рис. 3-31, а также 3-30). В этом случае, как и в предшествующем, радиатор тоже играет только роль маслопровода, поскольку при бесконечно большом коэффициенте теплоотдачи дли отвода тепла достаточно иметь очень малую поверхность у верхней части радиатора.

|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 |




