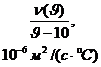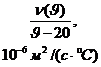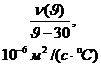Из формулы (3-26) для расчета перепада температуры ![]() , если скорость масла удвоить, т. е. вместо
, если скорость масла удвоить, т. е. вместо ![]() выбрать
выбрать ![]() , то новое значение перепада температуры
, то новое значение перепада температуры
![]() .
.
Таким образом, при удвоении скорости масла и без того малое значение ![]() уменьшится, но не в 2 раза, а составит примерно 88% первоначального значения. Удвоение теплового потока приводит к увеличению перепада температуры
уменьшится, но не в 2 раза, а составит примерно 88% первоначального значения. Удвоение теплового потока приводит к увеличению перепада температуры ![]() в
в 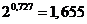 раза.
раза.
Увеличение скорости масла, например, с помощью насоса без увеличения теплоотдачи со стороны воздуха не приведет к существенному увеличению теплового потока радиатора. В случае принудительного движения воздуха увеличение скорости циркуляции масла становится обоснованным, поскольку масло при циркуляции за счет гравитационных сил и в связи с наличием гидравлического сопротивления в радиаторах может передавать соответствующий увеличенному коэффициенту теплоотдачи со стороны воздуха тепловой поток только при большом осевом перепаде температуры масла в радиаторе.
3-3. Потери давления в радиаторах
Средняя осевая вязкость масла в радиаторе
Введение такого понятия необходимо для расчета потери давления. Под средней осевой вязкостью масла в радиаторе высотой ![]() подразумевается величина, найденная по выражению
подразумевается величина, найденная по выражению
![]() (3-27)
(3-27)
где h–независимая переменная, равная расстоянию между верхней и рассматриваемой точками радиатора. Зависимость ![]() найдем, исходя из заданных зависимостей
найдем, исходя из заданных зависимостей ![]() и
и ![]() :
:
![]() .
.
Заменим пределы интегрирования, выраженные через предельные значения h, на соответствующие им температуры:
![]() (3-27a)
(3-27a)
Зависимость ![]() , соответствующая конденсаторному распределению температуры, определяется из уравнения (3-40):
, соответствующая конденсаторному распределению температуры, определяется из уравнения (3-40):
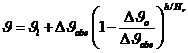 (3-28)
(3-28)
Поскольку ![]() найти проще, преобразуем
найти проще, преобразуем ![]() :
:
![]()
Дифференцируя уравнение (3-28), находим:
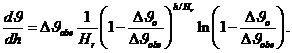 (3-28a)
(3-28a)
Тогда с учетом уравнений (3-6) и (3-28) получаем следующие выражения для средней осевой вязкости масла в радиаторе:
![]() (3-29)
(3-29)
Таблица 3-5
Значения функции 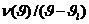 , необходимые для расчета средней осевой вязкости масла при различных температурах масла
, необходимые для расчета средней осевой вязкости масла при различных температурах масла ![]() и температурax воздуха,
и температурax воздуха, ![]()
|
|
|
|
25 | 1,8 | - | - |
30 | 1,05 | 2,1 | - |
35 | 0,68 | 1,132 | 3,4 |
40 | 0,467 | 0,7 | 1,4 |
45 | - | - | 0,765 |
50 | 0,243 | 0,323 | 0,485 |
60 | 0,14 | 0,175 | 0,233 |
70 | 0,09 | 0,118 | 0,135 |
80 | 0,06 | 0,07 | 0,084 |
90 | 0,0437 | 0,05 | 0,0583 |
100 | 0,0333 | 0,0376 | 0,0428 |
Если для 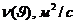 , в интервале температур
, в интервале температур ![]() воспользоваться зависимостью
воспользоваться зависимостью
![]() (3-30)
(3-30)
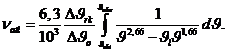 (3-31)
(3-31)

Рис. 3-16. Зависимость величины 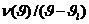 от температуры масла
от температуры масла ![]() при трех значениях температуры воздуха
при трех значениях температуры воздуха ![]() .
.
Определенный интеграл в уравнении (3-29) проще всего вычислить, если при заданном значении ![]() построить зависимость
построить зависимость 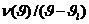 и полеченному графику найти площадь, ограниченную кривой, при предельных значениях температуры
и полеченному графику найти площадь, ограниченную кривой, при предельных значениях температуры ![]() . Для облегчения дальнейших расчетов зависимость
. Для облегчения дальнейших расчетов зависимость ![]() была рассчитана для значений
была рассчитана для значений ![]() исходя из данных табл. 1-1. По результатам этих расчетов, приведенных в табл. 3-5, были построены графики рис. 3-16.
исходя из данных табл. 1-1. По результатам этих расчетов, приведенных в табл. 3-5, были построены графики рис. 3-16.
Пример 3-2. Необходимо определить среднюю осевую вязкость масла ![]() для радиаторов, рассматривавшихся в предыдущем примере при
для радиаторов, рассматривавшихся в предыдущем примере при
![]() .
.
Согласно рис. 3-16 площадь, ограниченная кривой, соответствующей![]() , в интервале температур
, в интервале температур ![]() от 60 до 800С, дает значение искомого определенного интеграла
от 60 до 800С, дает значение искомого определенного интеграла
![]()
С учетом этого среднее значение вязкости масла
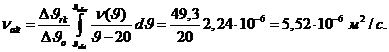
Потери давления в радиаторах
Пусть на трансформаторе установлено n радиаторов. Каждый радиатор состоит из z секций. Go – массовый расход масла, ![]() – средняя плотность масла, циркулирующего в радиаторах,
– средняя плотность масла, циркулирующего в радиаторах, ![]() – средняя осевая вязкость масла в радиаторах.
– средняя осевая вязкость масла в радиаторах.
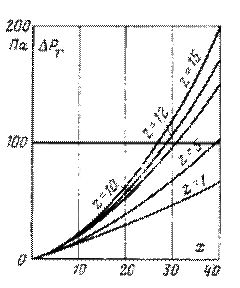
Рис. 3-17. Потери давления в радиаторах с расчетным числом секций.
По данным эксперимента потери давления ![]() , Па, в радиаторах, установленных на трансформаторе:
, Па, в радиаторах, установленных на трансформаторе:
![]() (3-32)
(3-32)
Для радиаторов по рис. 3-13 по данным измерений коэффициент С, кг/м6:
![]() (3-32а)
(3-32а)
где Нт – высота радиатора, м, и коэффициент В, кг/м7:
![]() . (3-32б)
. (3-32б)
Значение коэффициента В для обычно применяемого числа секций:
z | 1 | 5 | 10 | 12 | 15 |
| 5,9 | 29,4 | 58,8 | 70,6 | 88,0 |
Пусть ![]() , а среднее значение осевой вязкости
, а среднее значение осевой вязкости 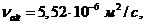 т. е. как в примере 3-2.
т. е. как в примере 3-2.
Произведение
![]()
Целесообразно 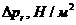 , представить как функцию параметра х, м3/с, где
, представить как функцию параметра х, м3/с, где
![]() (3-32в)
(3-32в)
Для расчета зависимости 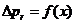 получены следующие уравнения:
получены следующие уравнения:
![]()
![]()
![]()
![]()
![]()
Кривые зависимости 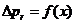 приведены на рис, 3-17.
приведены на рис, 3-17.
3-4. Потери давления в каналах обмотки
Для того чтобы при определении гидравлического сопротивления можно было воспользоваться известной формулой для ламинарного течения, оказалось целесообразным ввести такой приведенный радиальный размер вертикального масляного канала ![]() , который не зависел бы от его геометрических размеров, а зависел бы только от толщины пограничного слоя
, который не зависел бы от его геометрических размеров, а зависел бы только от толщины пограничного слоя ![]() . Пример расчета
. Пример расчета ![]() уже приводился. По данным измерений при радиальном размере вертикального масляного канала
уже приводился. По данным измерений при радиальном размере вертикального масляного канала 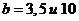 мм приведенный размер
мм приведенный размер 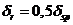 и
и 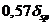 соответственно. При
соответственно. При 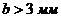 и
и 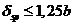 усредненно можно принять, что
усредненно можно принять, что
![]() (3-33)
(3-33)
Примерно 35% горизонтальной поверхности катушек закрыто прокладками и 20% вертикальной поверхности - рейками. Ширина вертикальных каналов, число которых совпадает с числом столбов прокладок, принимается равной длине дуги между прокладками и обозначается
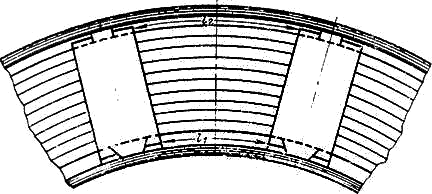
Рис. 3-18. К определению ширины вертикальных масляных каналов обмотки.
соответственно через ![]() и
и ![]() для внутренней и наружной поверхностей обмотки (рис. 3-18). Осевой размер вертикальных каналов совпадает с высотой обмотки
для внутренней и наружной поверхностей обмотки (рис. 3-18). Осевой размер вертикальных каналов совпадает с высотой обмотки
Гидравлические диаметры вертикальных каналов:
 (3-34)
(3-34)
Пусть средний гидравлический диаметр
![]() (3-34а)
(3-34а)
Используем его для дальнейших выводов.
Рассчитывать раздельно потери давления для внутреннего и наружного каналов нет смысла, так как это привело бы к физически невозможному результату. Давление во внутреннем и наружном каналах в точках, расположенных на одной и топ же высоте, должно быть одинаковым. Если это не соблюдается, то сразу между прокладками возникает радиальный поток, приводящий к выравниванию давления.
Примем, что потери в обмотке равны ![]() , осевой перепад температуры масла в обмотке
, осевой перепад температуры масла в обмотке ![]() , средняя плотность и средняя удельная теплоемкость масла
, средняя плотность и средняя удельная теплоемкость масла ![]() соответственно.
соответственно.
Объемный расход масла в вертикальных каналах
![]() (3-35)
(3-35)
Если через n обозначим число столбов прокладок по периметру, то суммарная площадь поперечного сечения потока масла в вертикальных каналах
![]() (3-36)
(3-36)
Проведенные измерения показали, что циркуляцию масла в вертикальных каналах обмоток нельзя уподобить ламинарному течению между двумя вертикальными плоскостями с параболическим распределением скоростей, так как движение масла здесь носит пограничный характер. Движущийся поток не заполняет весь радиальный размер канала. Гидравлическое сопротивление, рассчитанное исходя из полного радиального размера канала, оказывается, как это показали измерения, заниженным.
Максимальная скорость масла ![]() при параболическом распределении скоростей составляет 3/2 средней скорости. Тогда
при параболическом распределении скоростей составляет 3/2 средней скорости. Тогда
![]() (3-37)
(3-37)
При ламинарном течении жидкости в канале с гидравлическим диаметром ![]() и осевым размером
и осевым размером ![]() потери давления
потери давления
![]() (3-38)
(3-38)
где безразмерный коэффициент Е зависит от отношения сторон поперечного сечения канала (табл. 3-6);
Форма поперечного сечения |
| E |
Окружность с диаметром d | d | 64 |
Квадрат со стороной a | a | 57 |
Равносторонний треугольник со стороной a | 0,58a | 53 |
Кольцо шириной a | 2a | 96 |
Прямоугольник со сторонами a и b:
| 2a | 96 |
| 1,81a | 85 |
| 1,67a | 76 |
| 1,60a | 73 |
| 1,50a | 69 |
| 1,30a | 62 |
его значение для применяемых конструкций колеблется в пределах от 85 до 95.
Если в уравнение (3-38) подставить выражение
![]() ,
,
где ![]() - средняя вязкость масла в обмотке, и выражения (3-35) и (3-37) для
- средняя вязкость масла в обмотке, и выражения (3-35) и (3-37) для ![]() , то
, то
![]() (3-38а)
(3-38а)
3-5. Циркуляция воздуха в радиаторе и расчет перепада температуры между стенкой радиатора и воздухом
Конденсаторное распределение температуры
При расчете изменения температуры охлаждающей среды в теплообменнике обычно не учитывают изменение коэффициента теплоотдачи а или числа Nu вдоль поверхности, а вместо местного значения числа Nu используют его среднее значение или среднее значение ![]() .
.
В большинстве случаев пренебрегают тем фактом, что ![]() является степенной функцией перепада температуры. При этом дифференциальное уравнение для изменения температуры нагревающейся или охлаждающейся среды, которое выражает отнесенное к единице времени изменение количества теплоты и пропорциональное ему изменение температуры на пути dh шириной, равной единице, имеет вид:
является степенной функцией перепада температуры. При этом дифференциальное уравнение для изменения температуры нагревающейся или охлаждающейся среды, которое выражает отнесенное к единице времени изменение количества теплоты и пропорциональное ему изменение температуры на пути dh шириной, равной единице, имеет вид:
![]() (3-39)
(3-39)
Произведем разделение переменных:
![]() (3-39a)
(3-39a)
где
![]() (3-39б)
(3-39б)
После интегрирования правой и левой частей уравнения (3-39а) находим:
![]() (3-39в)
(3-39в)
где h – размер по высоте, отсчитываемый от верхней части радиатора.
Определим постоянные коэффициенты а и b в полученном уравнении (3-39в). Можно принять, что если ![]() , то
, то 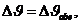 и если
и если ![]() , то
, то 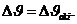 Тогда после соответствующих подстановок находим:
Тогда после соответствующих подстановок находим:
![]() (3-39г)
(3-39г)
![]()
![]() (3-39д)
(3-39д)
После подстановки в уравнение (3-39в) постоянных коэффициентов а и b получаем решение исходного дифференциального уравнения в виде
![]() (3-39е)
(3-39е)
![]()
![]() Преобразуем уравнение (3-39е), используя равенство
Преобразуем уравнение (3-39е), используя равенство![]()
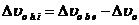
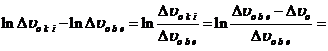
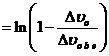
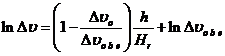 (3-39ж)
(3-39ж)
Перепад температуры между поверхностью и средой:
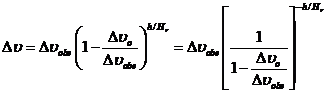 (3-40)
(3-40)
Это уравнение действительно в том случае, когда коэффициент теплоотдачи ![]() не зависит от перепада температуры
не зависит от перепада температуры ![]() .
.
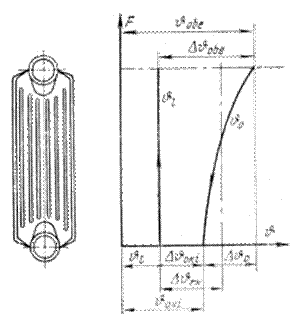
Рис. 3-19. Картина конденсаторного распределения температуры.
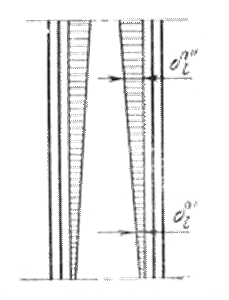
Рис, 3-20. Изменение толщины пограничного слоя по высоте радиатора. При небольшой высоте радиатора пограничные слои воздуха не соприкасаются между собой даже в верхней части радиатора.

|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 |