Радиаторная система охлаждения (стр. 7 )

Рис. 3-37. Зависимость плотности потока излучения от перепада температуры для ряда постоянных значений температуры воздуха

Число называется постоянной Стефана - Больцмана или константой излучения абсолютно черного тела и измеряется в Вт/(м2 К4). Степень черноты ,представляющая собой отношение коэффициентов излучения рассматриваемого и абсолютно черного тела, является безразмерным параметром, изменяющимся от единицы до нуля в зависимости от материала тела, состояния поверхности, ее цвета и температуры. Значения степени черноты некоторых материалов для встречающегося в трансформаторах диапазона температур от 0 до 1000С приведены в табл. 3-15.

Из данных табл. 3-15 видно, что для поверхности, покрытой алюминиевой краской, плотность потока излучения на 42% меньше, чем для поверхности, покрытой серой или зеленой краской. Для облегчения инженерных расчетов преобразуем уравнение (3-80), умножив величины, стоящие в скобках, на число 10-8 и заменив T1 на и Т2 на , поскольку уравнение в первую очередь используется для расчета плотности потока излучения радиатора или бака в окружающую среду с температурой. В этом случае уравнение для закона Стефана – Больцмана принимает вид:

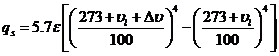(3-80а)

Излучающая поверхность

Излучающая поверхность равна поверхности, образованной наружной огибающей трансформатора независимо от того, насколько развита действительная поверхность. Принимается, что с поверхности трансформатора, обращенной вверх и равной проекции на горизонтальную плоскость, излучение происходит при температуре, равной наибольшей температуре масла , а с четырех его боковых поверхностей – при средней температуре масла. Площади поверхностей, обращенных вниз, не учитываются. Поверхность трансформатора является излучающей только в том случае, если она абсолютно черная или если значение ее степени черноты близко к единице

Таблица 3-16

Зависимость плотности потока излучения, от перепада температуры при 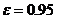и различных температурах окружающей среды

Этому требованию отвечают поверхности зеленого или серого цвета. При алюминиевой краске из-за наличия собственного, поглощенного и отраженного излучения у находящихся друг против друга поверхностей, излучающая поверхность меньше, чем поверхность трансформатора по его наружной огибающей.

Лучистый теплообмен между параллельными поверхностями

Пусть две параллельные поверхности размещены на таком близком расстоянии друг от друга, при котором излучением в перпендикулярные им боковые стороны можно пренебречь. Плотность потока излучения, передаваемого с поверхности 1 с термодинамической температурой T1 к поверхности 2 с термодинамической температурой Т2, определяется выражением

(3-81)

где – приведенная степень черноты системы поверхностей 1 и 2, определяемая по формуле

(3-81а)

где - степень черноты поверхности 1; – степень черноты поверхности 2.

Лучистый теплообмен в замкнутом пространстве

Если излучающая поверхность площадью с термодинамической температурой и степенью черноты охвачена поверхностью площадью с термодинамической температурой и степенью черноты , то плотность потока излучения на излучающей поверхности определяется формулой (3-81). В этом случае приведенная степень черноты

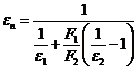(3-81б)

Такой лучистый теплообмен имеет место при размещении трансформатора в камере.

Влияние излучения солнца

Трансформатор с излучающей поверхностью площадью имеющей термодинамическую температуру и степень черноты, эксплуатируется при термодинамической температуре окружающего воздуха . Площадь облучаемой солнцем поверхности равна : Поверхность площадью имеет поглощательную способность по отношению к солнечным лучам, равную . Облучательная способность солнца равна Es. Тогда результирующее излучение поверхности площадью определяется плотностью потока излучения

(3-82)

Поглощательная способность, обозначенная через, зависит от материала поверхности площадью , ее цвета, шероховатости и является безразмерным числом, изменяющимся в пределах от 0 до 1 и показывающим, какую часть энергии солнечных лучей способна поглотить рассматриваемая поверхность. Значения поглощательной способности некоторых материалов приведены в табл. 3-17. Под облучательной способностью солнца Es, Вт/м2, подразумевается поток излучения, сообщаемый солнечными лучами единице площади поверхности. Значения облучательной способности солнца в летний солнечный день на 40-й параллели приведены в табл. 3-18.

Таблица 3-17

Значения поглощательной способности некоторых материалов в отношении солнечных лучей

Таблица 3-18

Значения, облучательной способности солнца в летний солнечный день на 40-й параллели

Средний угловой коэффициент

Заданы две поверхности и конечных размеров. Выберем некоторую расчетную поверхность , которая может совпадать с или с . Попадающая на поверхность часть энергии, излучаемой в полупространство элементарной площадкой поверхности , называется локальным угловым коэффициентом, который определяется из формулы

(3-83)

где r - расстояние между элементарной площадкой поверхности и элементарной площадкой в поверхности ; и– углы между линией, соединяющей центры элементарных площадок и , и нормалями к этим площадкам соответственно. Чтобы получить значение среднего углового коэффициента, надо взять интеграл от по поверхности F1 и разделить его на расчетную поверхность :

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8