Радиаторная система охлаждения (стр. 4 )

Выше было показано, что при естественной циркуляции масла и воздуха тепловой поток радиатора существенным образом зависит от коэффициента теплоотдачи со стороны воздуха и расхода масла. Ниже будет показано, что при высоте радиаторов, меньшем 1 м, температуру воздуха в радиаторе за пределами пограничного слоя можно принять постоянной. Расстояние между секциями радиатора достаточно велико, так что даже в верхней части радиатора пограничные слои/воздуха соседних секций не соприкасаются между собой, а это означает, что возникает так называемое конденсаторное распределение температуры, т. е. такое, какое имеет место при бесконечно большой теплоемкости воздуха. Картина конденсаторного распределения температуры зависит полностью от условий циркуляции воздуха, а процесс циркуляции масла не оказывает влияние на это распределение (рис. 3

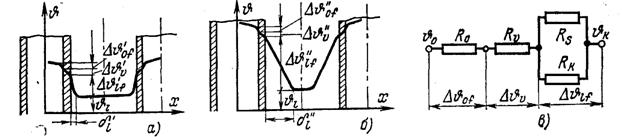
Рис. 3-21. Перепады температур в воздушном канале между двумя секциями и в масле у стенки радиатора при конденсаторном распределении температуры (а - внизу на входе в радиатор; б – вверху на выходе из радиатора; в - тепловая схема замещения).

Выше при получении уравнения температурной зависимости при конденсаторном распределении температуры (3-40) предполагалось, что коэффициент теплоотдачи со стороны воздуха не зависит от перепада температуры между стенкой радиатора и воздухом.

Для практических случаев критериальные уравнения для числа Nu (и соответственно уравнения для коэффициента теплоотдачи а со стороны воздуха) содержат перепад температуры между поверхностью и воздухом в степенях 0,125; 0,25 и 1/3 в зависимости от того, в каких пределах находится произведение GrPr для рассматриваемого процесса циркуляции. Выберем тот случай, для которого

(3-41)

Тогда дифференциальное уравнение (3-39) можно записать в виде

(3-42)

Произведем разделение переменных:

(3-42а)

где

(3-42б)

После подстановки постоянных коэффициентов N и С получаем решение исходного дифференциального уравнения в виде

(3-42в)

или

Определим постоянные коэффициенты N и С в полученном уравнении Можно принять, что если , то , и если

Тогда после соответствующих подстановок находим:

(3-42д)

(3-42е)

После подстановки постоянных коэффициентов N С получаем решение исходного дифференциального уравнения в виде

(3-42ж)

Перепад температуры между поверхностью и средой;

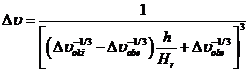(3-43)

если , то

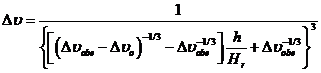(3-43а)

Если

(3-43б)

то

(3-43в)

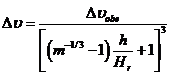(3-43г)

Если это выражение проинтегрировать в пределах от до и полученный результат разделить на ,то получим средний перепад температуры между поверхностью и воздухом

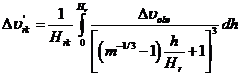(3-44)

Интегрирование проще всего выполнить, если подынтегральное выражение для согласно (3-43г) построить в виде графиков, как функцию т и , и графически определить соответствующую полученным кривым площадь, а затем для получения среднего перепада температуры полученную площадь разделить на .

Пример 3-3. Пусть =600С и = 40вС. Необходимо определить .

Согласно формуле (3-436)

Согласно формуле (3-43г)

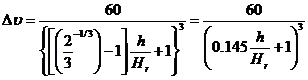
Определим значение при 10 значениях h/Hr. Результаты этих расчетов приведены в табл. 3-7.

Таблица 3-7

Значения функции 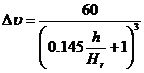для различных значений

Определим площадь, соответствующую значению интеграла. Для этого сложим через один значения , приведенные в табл. 3-7, и умножим сумму на два. Полученный результат разделим на 10 и тогда получим:

Этот результат ненамного отличается от логарифмической разности температур (49,30С) или от превышения средней температуры (500С)

Влияние высоты радиатора на коэффициент теплоотдачи со стороны воздуха

Если высота радиатора меньше критической, то коэффициент теплоотдачи радиатора со стороны воздуха определяется из критериального уравнения (2-9):

справедливого для циркуляции в бесконечном полупространстве.

Коэффициент С и показатель степени п зависят от значения величины , отнесенного к средней температуре пограничного слоя воздуха. Обычно и для этого диапазона и . В этом случае течение воздуха имеет турбулентный характер и выражение для коэффициента теплоотдачи геометрических размеров не содержит.

Коэффициент теплоотдачи со стороны воздуха определяется по формуле

(3-45)

При высоте радиатора, меньшей критической, для Ад справедлива приведенная выше формула (3-44) для среднего перепада температуры. Средний перепад температуры определяется в предположении, что толщина пограничного слоя воздуха даже в верхней части радиатора не настолько велика, чтобы при принятом между секциями радиатора расстоянии происходило соприкосновение соседних пограничных слоев воздуха. Это равнозначно принятию конденсаторного распределения температуры, которое предполагает присутствие воздушной массы, имеющей температуру окружающего воздуха и бесконечную теплоемкость.

Критическая высота радиатора

Для заданной конструкции радиатора всегда может быть найден, как функция средней температуры пограничного слоя и поверхностной плотности теплового потока, такой критический размер вдоль направления циркуляции, при котором пограничные слои воздуха соседних секций соприкасаются. Этот размер называется критической высотой радиатора. После соприкосновения соседних ламинарных пограничных слоев в охлаждающем воздушном канале радиатора образуется тонкий, прилипший к стенке ламинарный подслой, посередине канала воздух поднимается вверх, имея турбулентный режим течения, что увеличивает коэффициент теплоотдачи .

При высоте радиатора, превышающей критическую, конденсаторное распределение температуры становится недействительным и радиатор превращается в теплообменник с противотоком. Действительно, для такого радиатора поверхностная плотность теплового потока из-за увеличения и несмотря на уменьшение перепада температуры будет несколько больше, чем при значении , соответствующем ламинарному течению воздуха с конденсаторным распределением температуры.

Определим критическую высоту радиатора для заданной конструкции. Пусть расстояние между осями соседних секций равно 45 мм, а толщина секции – 10 мм. Это означает, что соседние пограничные слои воздуха соприкоснутся при толщине одного пограничного слоя

.

Увеличение толщины пограничного слоя при перемещении воздуха снизу вверх на расстояние х от нижней кромки радиатора определяется по известной формуле:

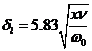(3-46)

где коэффициент кинематической вязкости воздуха, м2/с; w0– скорость потока воздуха за пределами пограничного слоя, м/с.

Таблица 3-8

Расстояния х' от нижней кромки радиатора до точки соприкосновения пограничных слоев воздуха при различных значениях средней температуры пограничного слоя т п скорости воздуха

Если в эту формулу подставить 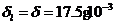м, то можно найти расстояние х', м, при котором пограничные слои соприкасаются:

(3-47)

Значения х' при различных значениях скорости w0 и средней температуры пограничного слоя приведены в табл. 3-8.

Из табл. 3-8 видно, что с уменьшением скорости воздуха и увеличением температуры пограничного слоя соприкосновение пограничных слоев наступает при меньших расстояниях х'.

Максимальная толщина ламинарного пограничного слоя и толщина турбулентного пограничного слоя

Если вдоль нагретой вертикальной стенки воздух движется со скоростью w0, то ламинарный пограничный слой на расстоянии от нижней кромки стенки переходит в турбулентный слой с тонким ламинарным подслоем.

Максимальная толщина ламинарного пограничного слоя - это толщина, относящаяся к расстоянию. Турбулентный пограничный слой образуется при достижении критического числа Re:

(3-48)

При этом

(3-48a)

Максимальную толщину ламинарного пограничного слоя находим при подстановке выражения (3-48а) для в формулу:

(3-49)

полученную из формулы (3-46)

(3-50)

Значения и для ряда значений скорости и средней температуры пограничного слоя приведены в табл. 3-9.

Из сравнения данных табл. 3-8 и 3-9 видно, что возникновение турбулентного режима течения воздуха между секциями радиаторов из-за соприкосновения пограничных слоев происходит при малом расстоянии от нижней кромки радиатора, а в случае вертикальной стенки, обращенной к свободному пространству, - только после прохождения воздухом нескольких метров пути вдоль стенки.

Таблица 3-9

Расстояния от нижней, кромки радиатора до тощи возникновения турбулентного пограничного слоя и максимальные толщины ламинарного пограничного слоя, при различных значениях, средней температуры пограничного слоя и скорости воздуха w0

Турбулентный пограничный слой образуется в точке на расстоянии от нижней кромки стенки. На расстоянии х от этой точки толщина турбулентного пограничного слоя определяется по формуле

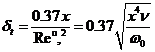(3-51)

Характер движения воздуха в радиаторах при естественном охлаждении

Будет ли режим течения воздуха в каналах между секциями радиаторов турбулентным или ламинарным, определяется значением числа. Известно, что при имеет место турбулентный режим течения.

Для того чтобы определить число Re, необходимо знать гидравлический диаметр dh. Для радиатора шириной 240 мм и с расстоянием между секциями 37 мм гидравлический диаметр

Таблица 3-10

Значение параметра при различных температурах воздуха

Значения коэффициента кинематической вязкости воздуха v и параметра dh/v приведены в табл. 3-10.

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8