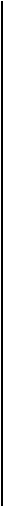Объединяя постоянную при переменной х, получим общее решение ![]() .
.
№ 000 [5]. Решить уравнение 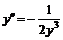 .
.
Решение
Уравнение не содержит переменную ![]() , поэтому понижение порядка осуществим с помощью замены
, поэтому понижение порядка осуществим с помощью замены 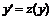 , тогда
, тогда ![]() . Подставим
. Подставим ![]() и
и ![]() в уравнение, получим
в уравнение, получим ![]() . Разделяя переменные, интегрируем
. Разделяя переменные, интегрируем  , откуда
, откуда ![]() , следовательно,
, следовательно, ![]() , или
, или ![]() . Интегрируя повторно, имеем:
. Интегрируя повторно, имеем:
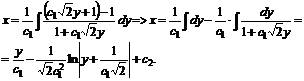
2.13.3 Задачи для самостоятельного решения
Выполнить задания № 000, 2917, 2918, 2920, 2926 [5].
2.13.4 Домашнее задание
1. Изучить теоретический материал по теме «Линейные однородные уравнения с постоянными коэффициентами, характеристическое уравнение. Уравнение с правой частью в виде многочлена, экспоненты, гармоники».
2. Выполнить задания № 000, 2921, 2932, 2934, 2939 [5].
2.14 Практическое занятие № 17. Линейные однородные уравнения с постоянными коэффициентами, характеристическое уравнение. Уравнение с правой
частью в виде многочлена, экспоненты, гармоники
2.14.1 Теоретические сведения и методические рекомендации по решению задач
Определение. Линейным дифференциальным уравнением n-го порядка называется уравнение вида
![]() .
.
Если ![]() – постоянные числа, а
– постоянные числа, а ![]() , то уравнение
, то уравнение
![]()
называется линейным однородным дифференциальным уравнением n-го порядка с постоянными коэффициентами.
Заменяя производные ![]() числами
числами ![]() получим уравнение
получим уравнение ![]() , называемое характеристическим.
, называемое характеристическим.
1) Если корни характеристического уравнения действительные и различные, то общее решение имеет вид 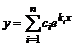 .
.
2) Если корень ![]() имеет кратность
имеет кратность ![]() , то
, то ![]() слагаемых в сумме
слагаемых в сумме ![]() заменяют произведением вида
заменяют произведением вида
![]() .
.
3) Если среди корней характеристического уравнения есть комплексные ![]() , то два слагаемых в сумме
, то два слагаемых в сумме 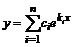 заменяют произведением вида
заменяют произведением вида ![]() .
.
4) Если среди корней характеристического уравнения есть
m-кратная пара сопряженных комплексных корней ![]() , то
, то ![]() пар слагаемых в сумме заменяют произведением вида
пар слагаемых в сумме заменяют произведением вида
![]()
Для уравнения 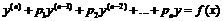 , где
, где ![]() – постоянные, рассмотрим метод неопределенных коэффициентов для нахождения частных решений:
– постоянные, рассмотрим метод неопределенных коэффициентов для нахождения частных решений:
а) если ![]() , то частное решение имеет вид
, то частное решение имеет вид 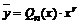 , где
, где ![]() – многочлен степени
– многочлен степени ![]() с неопределенными коэффициентами, а
с неопределенными коэффициентами, а ![]() – кратность корня
– кратность корня ![]() в характеристическом уравнении. Подставляя
в характеристическом уравнении. Подставляя 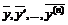 и приравнивая коэффициенты при одинаковых степенях
и приравнивая коэффициенты при одинаковых степенях ![]() , получим частное решение;
, получим частное решение;
б) если ![]() , то
, то ![]() , где
, где ![]() – кратность корня
– кратность корня ![]() в характеристическом уравнении. Коэффициенты многочлена
в характеристическом уравнении. Коэффициенты многочлена ![]() определяются по аналогии со случаем а);
определяются по аналогии со случаем а);
в) если 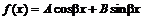 , то
, то ![]() , где
, где ![]() – кратность корня
– кратность корня ![]() в характеристическом уравнении;
в характеристическом уравнении;
г) если ![]() , то
, то
![]() , где
, где ![]() , а
, а ![]() – крат-
– крат-
ность корня 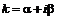 в характеристическом уравнении.
в характеристическом уравнении.
Приравнивая коэффициенты слева и справа при функциях ![]() и
и ![]() после подстановки
после подстановки ![]() найдем частное решение неоднородного уравнения.
найдем частное решение неоднородного уравнения.
Теорема (принцип наложения решений). Если правая часть
уравнения есть сумма вида 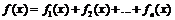 , то
, то
частное решение этого уравнения определяется равенством ![]() , где
, где ![]() – соответствующее частное решение уравнения
– соответствующее частное решение уравнения
![]() .
.
Метод вариации применим для нахождения решения линейного неоднородного уравнения n-го порядка как с переменными, так и с постоянными коэффициентами, если известно общее решение соответствующего однородного уравнения. Пусть определена фундаментальная система решений ![]() соответствующего однородного уравнения, тогда общее решение неоднородного уравнения будем искать в виде
соответствующего однородного уравнения, тогда общее решение неоднородного уравнения будем искать в виде
![]() ,
,
где функции ![]() определяются из системы уравнений
определяются из системы уравнений
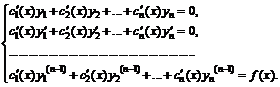
Определитель системы отличен от нуля, так как он является вронскианом, составленным из фундаментальной системы решений 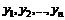 , следовательно, система имеет единственную совокупность решений
, следовательно, система имеет единственную совокупность решений 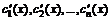 , интегрируя которую, получим искомые функции
, интегрируя которую, получим искомые функции ![]() .
.
2.14.2 Примеры решения задач
№ 000 [5]. Найти общее решение уравнения 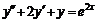 .
.
Решение
Характеристическое уравнение 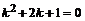 имеет двукрат-
имеет двукрат-
ный корень ![]() , следовательно, общее решение соответствующего однородного уравнения
, следовательно, общее решение соответствующего однородного уравнения ![]() . Правая часть заданного
. Правая часть заданного
уравнения ![]() , следовательно,
, следовательно, 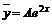 , так как
, так как ![]() . Дифференцируя
. Дифференцируя ![]() два раза и подставляя
два раза и подставляя ![]() ,
, ![]() ,
, ![]() в данное уравнение, получим
в данное уравнение, получим 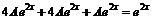 . Сокращая на
. Сокращая на ![]() , имеем
, имеем ![]() , откуда
, откуда ![]() , следовательно,
, следовательно, ![]() , а общее решение
, а общее решение 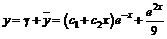 .
.
№ 000 [5]. Решить уравнение 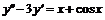 .
.
Решение
Характеристическое уравнение 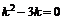 имеет корни
имеет корни ![]() , решение соответствующего однородного уравнения
, решение соответствующего однородного уравнения 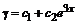 . Частное решение для правой части
. Частное решение для правой части ![]() есть сумма вида
есть сумма вида ![]() .
.
Дифференцируя, находим:
![]() ,
, ![]() .
.
Подставляя ![]() ,
, ![]() в исходное уравнение, получим:
в исходное уравнение, получим:
![]()
Приравнивая коэффициенты у подобных членов, разрешаем систему:
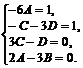
![]()
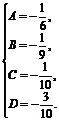
Частное решение определяется равенством
![]() , а общее решение есть сумма
, а общее решение есть сумма 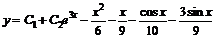 .
.
№ 000 [4]. Решить уравнение 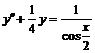 .
.
Решение
Соответствующее однородное уравнение имеет вид ![]() , а характеристическое уравнение
, а характеристическое уравнение ![]() имеет корни
имеет корни ![]() . На основании 3) общее решение исходного уравнения ищем в виде
. На основании 3) общее решение исходного уравнения ищем в виде ![]() .
.
Система для n=2 имеет вид
![]()
следовательно,
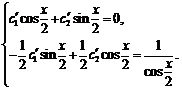
По формулам Крамера определим
![]() ,
, 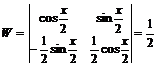 ,
,
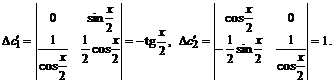
Интегрируя, имеем:
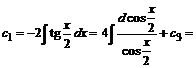
![]() ;
; ![]() .
.
Подставляя значения ![]() и
и ![]() в выражение
в выражение ![]()
![]() , получим общее решение неоднородного уравнения
, получим общее решение неоднородного уравнения 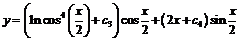 .
.
2.14.3 Задачи для самостоятельного решения
Выполнить задания № 000–3002, 3011, 3016 [5].
2.14.4 Домашнее задание
1. Изучить теоретический материал по теме «Решение систем дифференциальных уравнений».
2. Выполнить задания № 000, 3018–3022, 2973 [5].
2.15 Практическое занятие № 18. Решение систем дифференциальных уравнений
2.15.1 Теоретические сведения и методические рекомендации по решению задач
Система вида
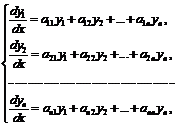
где коэффициенты ![]() – постоянные величины
– постоянные величины ![]() , называется системой линейных однородных дифференциальных уравнений с постоянными коэффициентами.
, называется системой линейных однородных дифференциальных уравнений с постоянными коэффициентами.
Частные решения системы найдем в виде
![]() ,
,
где ![]() – корни характеристического уравнения:
– корни характеристического уравнения:
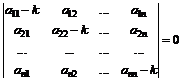 ,
,
а ![]() определяются системой
определяются системой
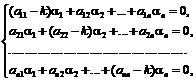 для каждого значения
для каждого значения ![]() .
.
Общее решение имеет вид
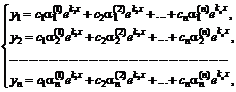
где ![]() – произвольные постоянные.
– произвольные постоянные.
2.15.2 Примеры решения задач
№ 000 [5]. Решить систему 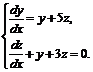
Решение
Дифференцируем по ![]() первое уравнение
первое уравнение ![]() , затем исключаем
, затем исключаем ![]() и
и ![]() из полученного уравнения и двух данных уравнений. В результате получим одно дифференциальное уравнение второго порядка с одной неизвестной функцией
из полученного уравнения и двух данных уравнений. В результате получим одно дифференциальное уравнение второго порядка с одной неизвестной функцией ![]() :
: ![]() . Решая его как линейное однородное уравнение с постоянными коэффициентами, найдем
. Решая его как линейное однородное уравнение с постоянными коэффициентами, найдем ![]() .
.
Вторую неизвестную функцию ![]() найдем из первого уравнения данной системы, подставив в него найденное выражение функции
найдем из первого уравнения данной системы, подставив в него найденное выражение функции ![]() и ее производной:
и ее производной:
![]() .
.
Следовательно, 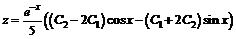 . Совокупность двух найденных функций есть искомое общее решение данной системы.
. Совокупность двух найденных функций есть искомое общее решение данной системы.
№ 000 [5]. Решить систему 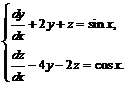
Решение
Дифференцируем по ![]() первое уравнение
первое уравнение ![]() ,
,
исключаем ![]() и
и ![]() из полученного уравнения и двух данных урав-нений. В результате получим одно дифференциальное уравнение
из полученного уравнения и двух данных урав-нений. В результате получим одно дифференциальное уравнение
второго порядка с одной неизвестной функцией ![]() :
: ![]() .
.
Интегрируя дважды, получим 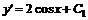 , следовательно,
, следовательно, ![]() .
.
Вторую неизвестную функцию ![]() найдем из первого уравнения данной системы, подставив в него найденное выражение
найдем из первого уравнения данной системы, подставив в него найденное выражение ![]() и ее производной, тогда
и ее производной, тогда ![]() .
.
Совокупность двух найденных функций 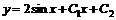 ,
, 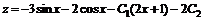 есть искомое общее решение данной системы.
есть искомое общее решение данной системы.
2.15.3 Задачи для самостоятельного решения
Выполнить задания № 000, 3086, 3089, 3090 [5].
2.15.4 Домашнее задание
1. Подготовиться к контрольной работе.
2. Выполнить задания № 000, 3080, 3083 [5].
2.16 Практическое занятие № 19. Контрольная работа по теме «Дифференциальные уравнения»
2.16.1 Домашнее задание
Изучить теоретический материал по теме «Вычисление двойного интеграла в декартовых координатах».
2.17 Практическое занятие № 20. Вычисление двойного
интеграла в декартовых координатах
2.17.1 Теоретические сведения и методические рекомендации по решению задач
Двойным интегралом от функции f(x, y) по области D называется предел интегральной суммы ![]() при стремлении к нулю шага разбиения области D
при стремлении к нулю шага разбиения области D
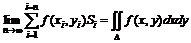 .
.
Теорема. Если функция f(x, y) непрерывна в замкнутой области D, то двойной интеграл ![]() существует.
существует.
Свойства двойного интеграла:
1) ![]()
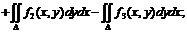
2) 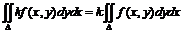 ;
;
3) если D = D1 + D2, то
![]() ;
;
4) теорема о среднем: двойной интеграл от функции f(x, y)
равен произведению значения этой функции в некоторой точке
области интегрирования на площадь области интегрирования
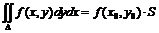 .
.
Теорема. Если функция f(x, y) непрерывна в замкнутой облас-
ти D, ограниченной линиями х = a, x = b, (a < b), y = j(x), y = y(x),
где j и y – непрерывные функции и j £ y, то
![]() .
.
Теорема. Если функция f(x, y) непрерывна в замкнутой области D, ограниченной линиями y = c, y = d (c < d), x = F(y), x = Y(y) (F(y) £ Y(y)), то
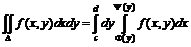 .
.
2.17.2 Примеры решения задач
№ 000 [4]. Изменить порядок интегрирования
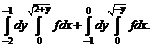
Решение
Построим область интегрирования на графике.
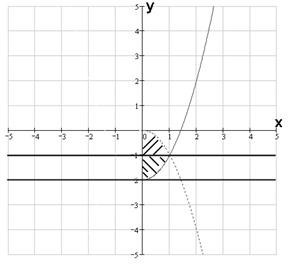
![]() .
.
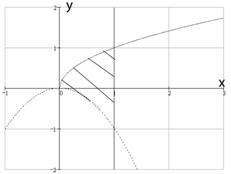
№ 000 [4]. Вычислить
![]()
Решение
Построим область интегрирования на графике.
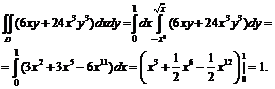
№ 000 [4]. Вычислить ![]()
Решение
Построим область интегрирования на графике.
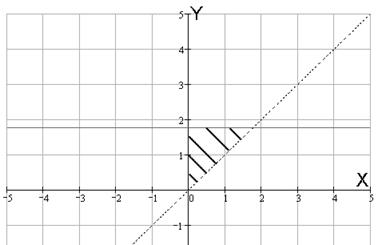
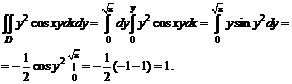
№ 000 [4]. Вычислить интеграл 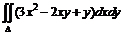 , если область интегрирования D ограничена линиями х = 0, х = у2, у = 2.
, если область интегрирования D ограничена линиями х = 0, х = у2, у = 2.
Решение
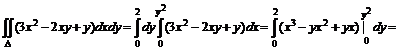
=![]() .
.
№ 000 [4]. Вычислить интеграл 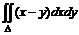 , если область D ограничена линиями y = 0, y = x2, x = 2.
, если область D ограничена линиями y = 0, y = x2, x = 2.
Решение
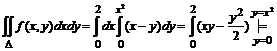
![]()
2.17.3 Задачи для самостоятельного решения
Выполнить задания № 000, 2119, 2122, 2125, 2132, 2136, 2137, 2143 [5].
2.17.4 Домашнее задание
1. Изучить теоретический материал по теме «Замена переменных в двойном интеграле».
2. Выполнить задания № 000, 2129, 2138, 2141, 2150 [5].
2.18 Практическое занятие № 21. Замена переменных в двойном интеграле
2.18.1 Теоретические сведения и методические рекомендации по решению задач
Рассмотрим двойной интеграл вида 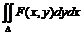 , где переменная х изменяется в пределах от a до b, а переменная у – от j1(x) до j2(х). Положим х = f(u, v), y = j(u, v), тогда замена переменных осуществляется по формуле
, где переменная х изменяется в пределах от a до b, а переменная у – от j1(x) до j2(х). Положим х = f(u, v), y = j(u, v), тогда замена переменных осуществляется по формуле
![]() ,
,
выражение 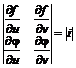 называется определителем Якоби, или якобианом.
называется определителем Якоби, или якобианом.
Для вычисления двойного интеграла в полярных координатах воспользуемся формулами перехода от декартовых координат к полярным 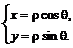
В этом случае якобиан имеет вид
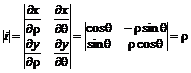 ,
,
тогда
![]()
где t – новая область значений;
![]()
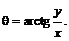
2.18.2 Примеры решения задач
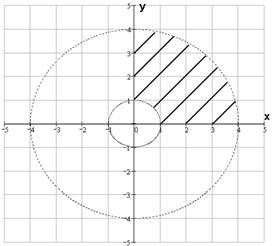
№ 000 [4]. Пластинка ![]() задана ограничивающими ее кри-
задана ограничивающими ее кри-
выми ![]()
где ![]() – поверхностная плотность. Найти массу пластинки.
– поверхностная плотность. Найти массу пластинки.
Решение
В полярной системе координат
![]()
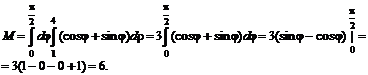
№ 000 [4]. Пластинка ![]() задана ограничивающими ее кривыми
задана ограничивающими ее кривыми
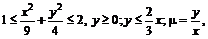 где
где ![]() – поверхностная плотность. Найти массу пластинки.
– поверхностная плотность. Найти массу пластинки.
Решение
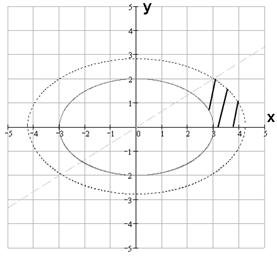
Обобщенная полярная система координат
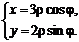
Найдем якобиан перехода
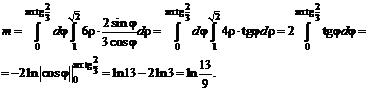
2.18.3 Задачи для самостоятельного решения
Выполнить задания № 000–2170 [5].
2.18.4 Домашнее задание
1. Изучить теоретический материал по теме «Приложения двойного интеграла».
2. Выполнить задания № 000, 2164, 2165, 2181 [5].
2.19 Практическое занятие № 22. Приложения двойного
интеграла
2.19.1 Теоретические сведения и методические рекомендации по решению задач
Рассмотрим геометрические и физические приложения кратных интегралов.
2.19.1.1 Вычисление площадей в декартовых координатах
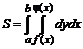 .
.
2.19.1.2 Вычисление площадей в полярных координатах
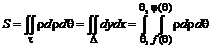 .
.
2.19.1.3 Вычисление объемов тел
Пусть тело ограничено снизу плоскостью Оху, сверху – поверхностью z = f(x, y), а с боков – цилиндрической поверхностью, тогда объем определяется формулой
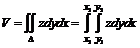 .
.
2.19.1.4 Вычисление площади кривой поверхности
Если поверхность задана уравнением z = j(x, y), то площадь поверхности вычисляется по формуле
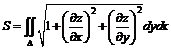 .
.
2.19.1.5 Вычисление моментов инерции площадей плоских фигур
Пусть площадь плоской фигуры (область D) ограничена линией, уравнение которой f(x, y) = 0. Тогда моменты инерции этой фигуры находятся по формулам
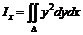 ,
, ![]() ,
, 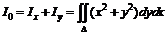 .
.
2.19.1.6 Вычисление центров тяжести площадей плоских фигур
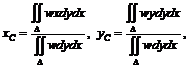
где w – поверхностная плотность.
2.19.2 Примеры решения задач
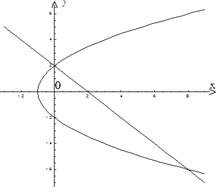
№ 000 [4]. Вычислить площадь фигуры, ограниченной линиями y2 = 4x + 4, x + y – 2 = 0.
Решение
Построим графики заданных функций.
Линии пересекаются в двух точках (0, 2) и (8, -6). Таким образом, область интегрирования ограничена по оси Ох графиками кривых от ![]() до х = 2 – у, а по оси Оу от (-6) до 2. Тогда искомая площадь равна
до х = 2 – у, а по оси Оу от (-6) до 2. Тогда искомая площадь равна
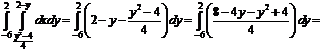
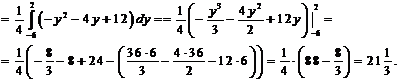
№ 000 [4]. Найти площадь фигуры, ограниченной линиями 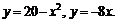
Решение
Построим область интегрирования на графике.
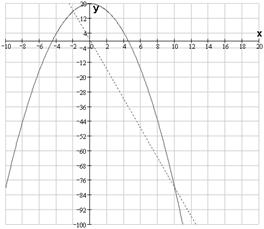
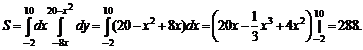
№ 000 [4]. Вычислить объем, ограниченный поверхностями
x2 + y2 = 1, x + y + z =3 и плоскостью ХОY.
Решение
Пределы интегрирования
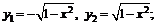 x1 = -1; x2 = 1.
x1 = -1; x2 = 1.
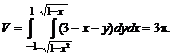
2.19.3 Задачи для самостоятельного решения
Выполнить задания № 000, 2186, 2194, 2201, 2215, 2227,
2230 [5].
2.19.4 Домашнее задание
1. Изучить теоретический материал по теме «Вычисление тройного интеграла в декартовых координатах».
2. Выполнить задания № 000, 2195, 2199, 2218, 2231 [5].
2.20 Практическое занятие № 23. Вычисление тройного интеграла в декартовых координатах
2.20.1 Теоретические сведения и методические рекомендации по решению задач
Определение. Тройным интегралом называется предел вида
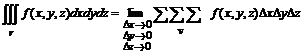 ,
,
где суммирование производится по области v, которая ограничена некоторой поверхностью j(x, y, z) = 0.
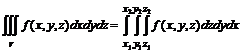 ,
,
где х1 и х2 – постоянные величины; у1 и у2 могут быть некоторыми функциями от х или постоянными величинами; z1 и z2 могут быть функциями от х и у или постоянными величинами.
2.20.2 Примеры решения задач
№ 000 [4]. Вычислить интеграл 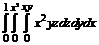 .
.
Решение
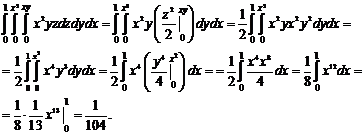
№ 000 [4]. Вычислить
![]() V:
V: ![]()
Решение
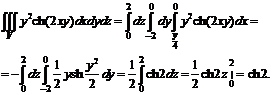
№ 000 [4]. Вычислить
![]()
![]()
Решение
![]()
2.20.3 Задачи для самостоятельного решения
Выполнить задания № 000, 2244, 2247, 2249, 2250 [5].
2.20.4 Домашнее задание
1. Изучить теоретический материал по теме «Замена переменных в тройном интеграле. Цилиндрические и сферические координаты».
2. Выполнить задания № 000, 2243, 2248, 2251 [5].
2.21 Практическое занятие № 24. Замена переменных в тройном интеграле. Цилиндрические и сферические координаты
2.21.1 Теоретические сведения и методические рекомендации по решению задач
Операция замены переменных в тройном интеграле аналогична соответствующей операции для двойного интеграла
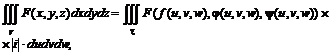
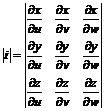 .
.
Связь координат произвольной точки Р пространства в цилиндрической системе с координатами в декартовой прямоугольной системе осуществляется по формулам
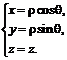
![]()
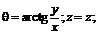

Формула перехода
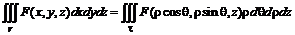 .
.
Связь координат произвольной точки Р пространства в сферической системе с координатами в декартовой прямоугольной системе осуществляется по формулам
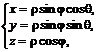
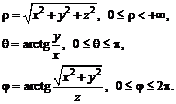
Сферические координаты принято называть соответственно ![]() –широтой,
–широтой, ![]() – долготой,
– долготой, ![]() – радиус-вектором.
– радиус-вектором.
Для представления тройного интеграла в сферических координатах вычислим якобиан
 Формула перехода
Формула перехода
![]() .
.
2.21.2 Примеры решения задач
№ 000 [4]. Найти объем тела, заданного ограничивающими его поверхностями ![]()
![]()
![]()
Решение
Построим проекцию тела на плоскость ХОY.
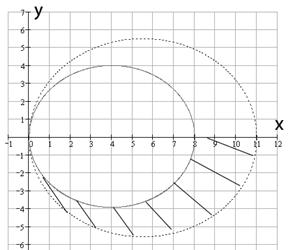
Цилиндрические координаты
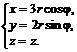
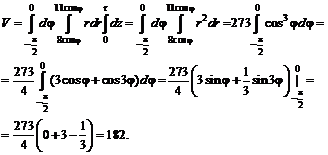
№ 000 [4]. Найти объем тела, заданного ограничивающими его поверхностями ![]()
Решение
Цилиндрические координаты
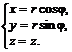
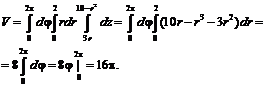
№ 000 [4]. Найти объем тела, заданного ограничивающими его поверхностями ![]()
Решение
В сферической системе координат
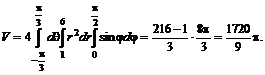
2.21.3 Задачи для самостоятельного решения
Выполнить задания № 000, 2256, 2257, 2258 [5].
2.21.4 Домашнее задание
1. Изучить теоретический материал по теме «Приложения тройного интеграла».
2. Выполнить задания № 000, 2253, 2255 [5].
2.22 Практическое занятие № 25. Приложения тройного интеграла
2.22.1 Теоретические сведения и методические рекомендации
по решению задач
Если поверхность тела описывается уравнением f(x, y, z) = 0, то объем тела может быть найден по формуле
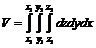 .
.
Координаты центра тяжести тела определяются равенствами
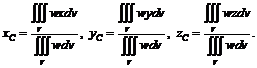
Моменты инерции тела относительно осей координат определяются по формулам
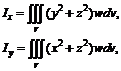
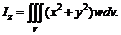
Момент инерции тела относительно начала координат
![]()
В приведенных формулах w – плотность тела в точке (х, у, z),
dv – элемент объема.
Масса неоднородного тела определяется формулой
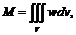 где плотность w – величина переменная.
где плотность w – величина переменная.
2.22.2 Примеры решения задач
№ 000 [4]. Найти объем тела, заданного ограничивающими его поверхностями ![]()
Решение
Построим проекцию тела на плоскость ХОY.
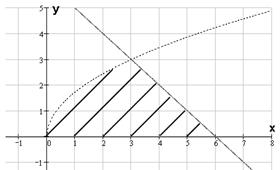
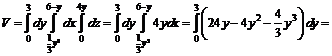
![]()
№ 000 [4]. Тело задано ограничивающими его поверхностями
![]() где μ –плотность. Найти массу тела.
где μ –плотность. Найти массу тела.
Решение
Цилиндрическая система координат
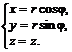
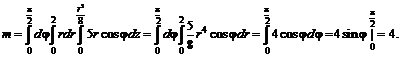
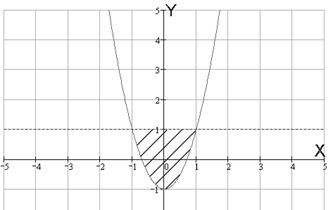
№ 000 [4]. Найти объем тела, заданного ограничивающими его поверхностями ![]()
Решение
Проекция на XOY представлена на рисунке.
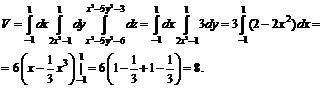
2.22.3 Задачи для самостоятельного решения
Выполнить задания № 000, 2262, 2263, 2266, 2267 [5].
2.22.4 Домашнее задание
1. Изучить теоретический материал по теме «Сходимость числовых рядов. Функциональные ряды».
2. Выполнить задания № 000, 2261, 2265, 2268 [5].
3 ПОРЯДОК ПРОВЕДЕНИЯ ЗАНЯТИЙ
Занятия № 1–7, 9–18, 20–25 проходят в следующем порядке:
1) формулируется тема занятия, поясняется связь темы с другими темами учебной дисциплины;
2) проверяется готовность студентов к занятию;
3) занятие проводится согласно тематике и в соответствии с рабочей программой дисциплины.
На занятиях № 8, 19 студентам предлагается решить контрольные работы.
ЛИТЕРАТУРА
1. Бугров, и интегральное исчисления / , . – М.: Наука, 1999.
2. Бугров, уравнения. Кратные интегралы. Ряды. Функция комплексного переменного / , . – М.: Наука, 1985.
3. Пискунов, и интегральное исчисления: в 2 т. / . – М.: Наука, 1985.
4. Задачи и упражнения по математическому анализу / под ред. . – М.: Наука, 1985.
5. Задачи и упражнения по математическому анализу / под ред. . – М.: Наука, 1985.
6. Кудрявцев, математического анализа / . – М.: Наука, 1985.
Учебное издание
Тушкина Татьяна Михайловна
Ростова Ольга Дмитриевна
Кувшинова Лидия Павловна
МАТЕМАТИКА
В четырёх частях
Часть вторая
Неопределенный и определенный
интегралы. Дифференциальное исчисление
функции двух переменных.
Дифференциальные уравнения.
Двойные и тройные интегралы
Методические рекомендации по проведению
практических занятий для студентов специальностей
151900 – «Конструкторско-технологическое обеспечение
машиностроительных производств», 170100 – «Боеприпасы
и взрыватели», 160700 – «Проектирование авиационных
и ракетных двигателей», 230400 – «Информационные
системы и технологии»
Редактор
Технический редактор
Подписано в печать 17.02.12. Формат 60´84 1/16
Усл. п. л. 5,17. Уч.-изд. л. 5,56
Печать – ризография,
множительно-копировальный аппарат «RISO ЕZ300»
Тираж 54 экз. Заказ 2012-19
Издательство Алтайского государственного
технического университета
г. Барна
Оригинал-макет подготовлен ИИО БТИ АлтГТУ
Отпечатано в ИИО БТИ АлтГТУ
7
МАТЕМАТИКА. В четырёх частях |
Часть 2 Неопределенный и определенный Дифференциальные уравнения. Двойные и тройные интегралы Методические рекомендации по проведению 151900 – «Конструкторско-технологическое обеспечение машиностроительных производств», 170100 – «Боеприпасы |
Бийскö2012

|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 |