.
Метод интегрирования по частям основан на известной формуле производной произведения (uv)¢ = u¢v + v¢u, где u и v – некоторые функции от х. В дифференциальной форме: d(uv)=udv+vdu.
Проинтегрировав, получаем 
.
В соответствии со свойствами неопределенного интеграла
.
Получили формулу интегрирования по частям, которая позволяет находить интегралы многих элементарных функций.
2.1.2 Примеры решения задач
№ 000 [4]. Найти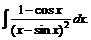 
Решение
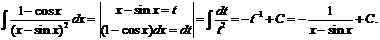№ 000 [4]. Найти неопределённый интеграл 
.
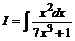Решение
Подведем под знак дифференциала знаменатель подынтегральной дроби
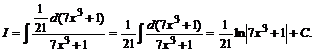
№ 000 [4]. Найти 
.
Решение
№ 000 [4]. Найти неопределённый интеграл 
.
Решение
Введем подстановку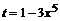 
, откуда 
. Тогда 
. Находим полученный табличный интеграл и возвращаемся к старой переменой
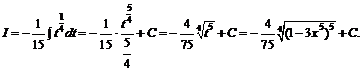
№ 000 [4]. Найти неопределённый интеграл 
.
Решение
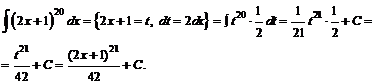
№ 000 [4]. Найти неопределённый интеграл 
.
Решение
Применим формулу интегрирования по частям
.
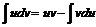В данном случае
.
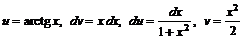Подставляя эти выражения в формулу, получим:
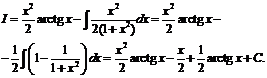
№ 000 [4]. Найти неопределённый интеграл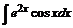
.
Решение
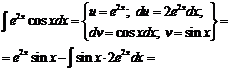
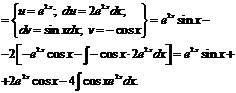
Полученный интеграл совпадает с исходным, перенесем его в левую часть равенства.
№ 000 [4]. Найти 
Решение
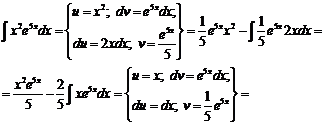
2.1.3 Задачи для самостоятельного решения
Выполнить задания № 000, 1036, 1043–1046, 1063, 1068, 1072, 1084, 1101, 1122, 1191, 1192, 1198, 1212, 1215, 1221, 1228, 1235 [5].
2.1.4 Домашнее задание
1. Изучить теоретический материал по теме «Интегрирование простейших дробей и рациональных дробей».
2. Выполнить задания № 000, 1199, 1216, 1223, 1232, 1236 [5].
2.2 Практическое занятие № 3. Интегрирование простейших дробей и рациональных дробей
2.2.1 Теоретические сведения и методические рекомендации по решению задач
Определение. Элементарными называются дроби следующих четырех типов:
I |
| |
II |
| |
III |
| |
IV |
|
,где m, n – натуральные числа (m ³ 2, n ³ 2) и b2 – 4ac <0.
Первые два типа интегралов от элементарных дробей приводятся к табличным подстановкой t = ax + b.
I 
II 
.
Интеграл дроби вида III может быть представлен в виде
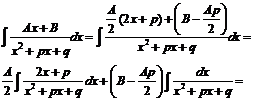
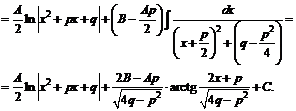
Здесь в общем виде показано приведение интеграла дроби вида III к двум табличным интегралам.
Рассмотрим теперь методы интегрирования простейших дробей IV типа. Сначала рассмотрим частный случай при М = 0, N = 1. Тогда интеграл вида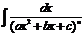 
можно путем выделения в знаменателе полного квадрата представить в виде 
.
Выполним следующее преобразование:
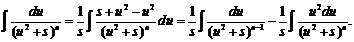Второй интеграл, входящий в это равенство, интегрируем по частям.
.
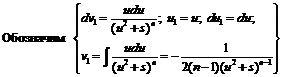Для исходного интеграла получаем
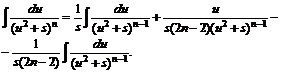
Полученная формула называется рекуррентной.
Если применить ее (n–1) раз, то получится табличный интеграл 
. Вернемся теперь к интегралу от элементарной дроби вида IV в общем случае.
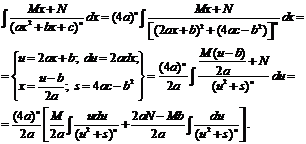
В полученном равенстве первый интеграл с помощью подстановки t = u2 + s приводится к табличному 
, а ко второму интегралу применяется рекуррентная формула.
Теорема. Если 
– правильная рациональная дробь, знаменатель P(x) которой представлен в виде произведения линейных
и квадратичных множителей (отметим, что любой многочлен с дей-ствительными коэффициентами может быть представлен в таком виде:
P(x) = (x – a)a…(x – b)b(x2 + px + q)l…(x2 + rx + s)m ), то эта дробь может быть разложена на элементарные по следующей схеме:
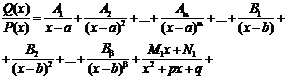
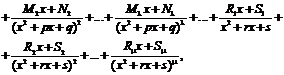
где Ai, Bi, Mi, Ni, Ri, Si – некоторые постоянные величины.
При интегрировании рациональных дробей прибегают к разложению исходной дроби на элементарные. Для нахождения величин Ai, Bi, Mi, Ni, Ri, Si применяют метод неопределенных коэффициентов, суть которого состоит в том, что для тождественного равенства двух многочленов необходимо и достаточно, чтобы были равны коэффициенты при одинаковых степенях х.
2.2.2 Примеры решения задач
№ 000 [4]. Найти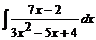 
.
Решение
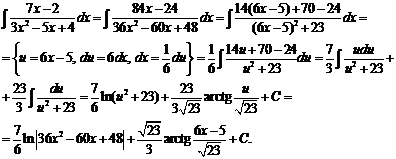
№ 000 [4]. Найти 
Решение
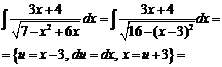
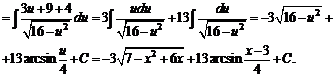
№ 000 [4]. Найти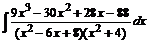 
.
Решение
Так как (
, то
.
Приводя к общему знаменателю и приравнивая соответствующие числители, получаем:
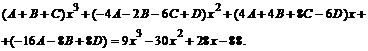
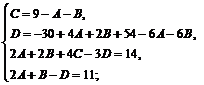
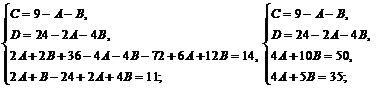
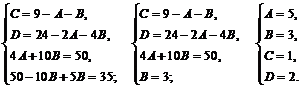
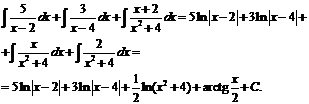
2.2.3 Задачи для самостоятельного решения
Выполнить задания № 000, 1259, 1262, 1265, 1281, 1285, 1287, 1291 [5].
2.2.4 Домашнее задание
1. Изучить теоретический материал по теме «Интегрирование выражений, содержащих тригонометрические и гиперболические функции».
2. Выполнить задания № 000, 1284, 1294, 1314 [5].
2.3 Практическое занятие № 4. Интегрирование выражений, содержащих тригонометрические и гиперболические функции
2.3.1 Теоретические сведения и методические рекомендации
по решению задач
Интегралы вида 
преобразуют с помощью подстановки 
, в новых переменных имеем
, 
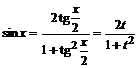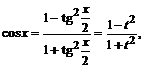
тогда
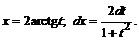
Таким образом,
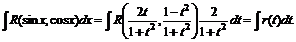
Введенное преобразование называется универсальной тригонометрической подстановкой.
В интегралах вида 
, где функция R является нечетной относительно cosx, рационально применить подстановку 
. 
.
Функция 
может содержать cosx только в четных степенях, а следовательно, может быть преобразована в рациональную функцию относительно sinx.
В интегралах вида , где функция R является нечетной относительно sinx, используют подстановку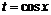 
. Тогда 
В интегралах вида , где функция R четная относительно sinx и cosx, используется подстановка 
. Тогда 
.
В интегралах произведения синусов и косинусов различных аргументов применяется одна из следующих трех формул:
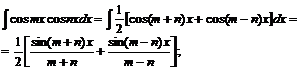
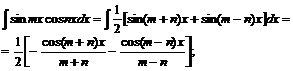
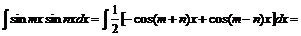
Также при интегрировании тригонометрических функций используют формулы
, 
, 
.
Для интегралов вида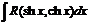 
применяется универсаль-
ная гиперболическая подстановка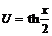 
, тогда 
, 
, 
.
Для интегралов вида 
исполь-зуется подстановка 
, тогда 
, 
, 
. Формулы понижения степени для гиперболических функций имеют вид 
, 
.
Если в интеграле 
, где 
, то проводят преобразование 
, т. к. 
.
2.3.2 Примеры решения задач
№ 000 [4]. Найти 
.
Решение
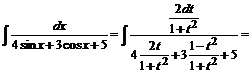
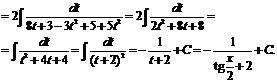
№ 000 [4]. Найти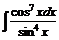
.
Решение
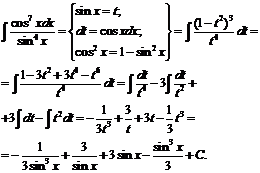
№ 000 [4]. Найти
Решение
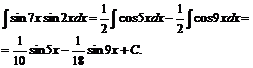
№ 000 [4]. Найти
Решение
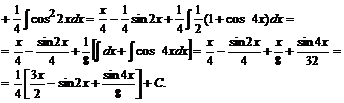
№ 000 [4]. Найти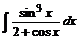
.
Решение
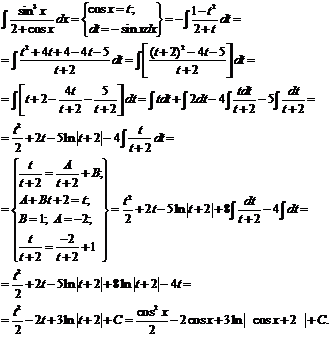
№ 000 [4]. Найти
.
Решение
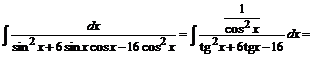
№ 000 [4]. Найти 
.
Решение
.
№ 000 [4]. Найти 
.
Решение
Введем замену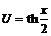 
, откуда 
, 
.
В новых переменных имеем
.
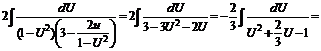
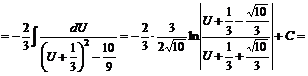
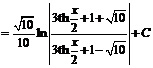2.3.3 Задачи для самостоятельного решения
Выполнить задания № 000, 1342, 1353, 1356, 1362, 1365, 1373, 1382, 1391, 1393, 1395, 1397, 1400, 1402, 1484 [5].
2.3.4 Домашнее задание
1. Изучить теоретический материал по теме «Интегрирование иррациональных выражений».
2. Выполнить задания № 000, 1354, 1360, 1371, 1442, 1443, 1466, 1392, 1394, 1398, 1485, 1486, 1487 [5].
2.4 Практическое занятие № 5. Интегрирование иррациональных выражений
2.4.1 Теоретические сведения и методические рекомендации
по решению задач
В интегралах вида 
, где n – натуральное число, функция рационализируется с помощью подстановки 
.
Если в состав иррациональной функции входят корни различных степеней, то в качестве новой переменной рационально взять корень степени, равной наименьшему общему кратному степеней корней, входящих в выражение.
Определение. Биноминальным дифференциалом называется выражение xm(a + bxn)pdx, где m, n, и p – рациональные числа. Интеграл от биноминального дифференциала может быть выражен через элементарные функции в следующих трех случаях:
1) если р – целое число, то интеграл рационализируется с помощью подстановки 
, где l – общий знаменатель m и n;
2) если 
– целое число, то интеграл рационализируется подстановкой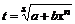 
, где s – знаменатель дроби р;
3) если 
– целое число, то используется подстановка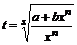 
, где s – знаменатель дроби р.
Интегралы вида 
путем выделения полного квадрата могут быть приведены к одному из следующих трех типов:
1) 
2) 
3) 
Интеграл вида 
подстановкой 
или 
сводится к интегралу от рациональной функции относительно sint или cost.
Интеграл вида 
подстановкой 
или 
сводится к интегралу от рациональной функции относительно sint и cost.
Интеграл вида 
подстановкой 
или 
сводится к интегралу от рациональной функции относительно sint или cost.
Подстановки Эйлера используют при следующих условиях:
1) если а>0, то интеграл вида 
рационализируется подстановкой 
;
2) если a<0 и c>0, то интеграл вида рационализируется подстановкой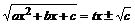 
;
3) если a<0, а подкоренное выражение раскладыва-
ется на действительные множители a(x – x1)(x – x2), то интег-
рал вида рационализируется подстановкой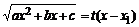 
.
Рассмотрим интегралы следующих трех типов:
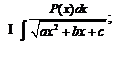
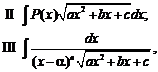
где P(x) – многочлен, n – натуральное число. Причем интегралы II и
III типов могут быть приведены к виду интеграла I типа.
Выполним следующее преобразование:
в этом выражении Q(x) – некоторый многочлен, степень которого ниже степени многочлена P(x) на единицу, а l – некоторая постоянная величина.
Для нахождения неопределенных коэффициентов многочлена Q(x), степень которого ниже степени многочлена P(x), дифференцируют обе части полученного выражения, затем умножают на 
и, сравнивая коэффициенты при одинаковых степенях х, определяют величину l и коэффициенты многочлена Q(x).
2.4.2 Примеры решения задач
№ 000 [4]. Найти 
.
Решение
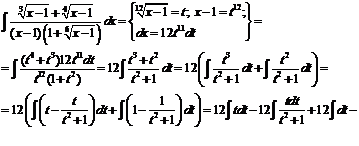
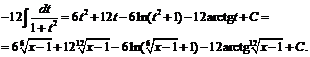
№ 000 [4]. Найти 
Решение
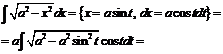
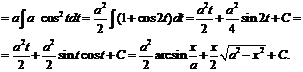
№ 000 [4]. Найти 
Решение
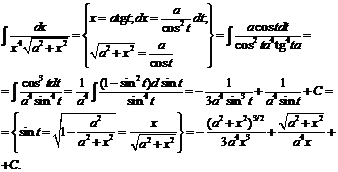
№ 000 [4]. Найти 
.
Решение
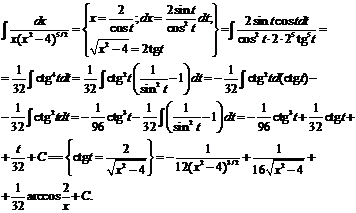
№ 000 [4]. Найти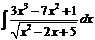 
.
Решение
Продифференцируем полученное выражение, умножим на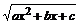 
и сгруппируем коэффициенты при одинаковых степе-
нях х.
=
;
=
.
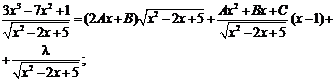
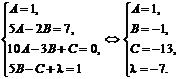
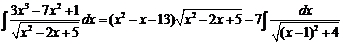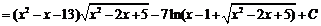№ 000 [4]. Найти 
.
Решение
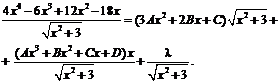
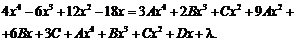
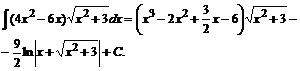
2.4.3 Задачи для самостоятельного решения
Выполнить задания № 000, 1203, 1315–1320, 1328, 1334 [5].
2.4.4 Домашнее задание
1. Изучить теоретический материал по теме «Вычисление определенного интеграла: интегрирование по частям и подстановкой. Несобственные интегралы. Комплексные числа».
2. Выполнить задания № 000, 1321, 1322, 1327, 1335 [5].
2.5 Практические занятия № 6–7. Вычисление определенного интеграла: интегрирование по частям и подстановкой.
Несобственные интегралы
2.5.1 Теоретические сведения и методические рекомендации по решению задач
Определение. Если для функции f(x) существует предел 
, равный
то функция называется интегрируемой на отрезке [a, b].
Свойства определенного интеграла:
1) 
2) 
;
3) 
;
4) если f(x) £ j(x) на отрезке [a, b], где a < b, то
;
5) если m и M – соответственно наименьшее и наибольшее значения функции f(x) на отрезке [a, b], то
;
6) теорема о среднем: если функция f(x) непрерывна на отрезке [a, b], то на этом отрезке существует точка e такая, что
;
7) для произвольных чисел a, b, c справедливо равенство
;
8) 
.
Теорема Ньютона–Лейбница. Если функция F(x) – какая-либо первообразная от непрерывной функции f(x), то
.
Приемы вычисления определенных интегралов практически не отличаются от всех тех приемов и методов, которые были рассмотрены при нахождении неопределенных интегралов.
Точно так же применяются методы подстановки (замены переменной), метод интегрирования по частям, те же приемы нахождения первообразных для тригонометрических, иррациональных и трансцендентных функций. Особенностью является только то, что при применении этих приемов надо распространять преобразование не только на подынтегральную функцию, но и на пределы интегрирования.
Пусть задан интеграл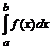 
, где f(x) – непрерывная функция на отрезке [a, b]. Введем новую переменную в соответствии с формулой x=j(t). Если:
1) j(a) = а, j(b) = b;
2) j(t) и j¢(t) непрерывны на отрезке [a, b];
3) f(j(t)) определена на отрезке [a, b],
то
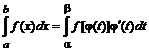
или
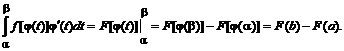
Определение. Если существует конечный предел 
, то этот предел называется несобственным интегралом от функции f(x) на интервале [a, ¥). Обозначение: 
.
Если этот предел существует и конечен, то говорят, что несобственный интеграл сходится, если предел не существует или бесконечен, то несобственный интеграл расходится. Аналогичные рассуждения можно привести для несобственных интегралов вида
, 
.
Теорема. Если для всех х (x³a) выполняется условие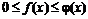 
и интеграл 
сходится, то 
также сходится.
Теорема. Если для всех х (x³a) выполняется условие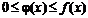 
и интеграл 
расходится, то также расходится.
Если в точке х = с функция либо не определена, либо разрывна, то
.
Если интеграл существует, то интеграл 
сходится, если интеграл не существует, то расходится.
Если в точке х = а функция терпит разрыв, то
.
Если функция f(x) имеет разрыв в точке b на промежутке [a, с], то 
. Таких точек внутри отрезка может быть несколько. Если сходятся все интегралы, входящие в сумму, то сходится и суммарный интеграл.
2.5.2 Примеры решения задач
№ 000 [4]. Вычислить определенный интеграл 
Решение
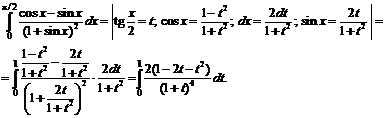
Разложим дробь 
на простейшие
|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 |
