Данное уравнение сводится к дифференциальному уравнению с разделяющимися переменными с помощью подстановки ![]() , где
, где ![]() – новая неизвестная функция.
– новая неизвестная функция.
2.10.2 Примеры решения задач
№ 000 [5]. Решить дифференциальное уравнение
![]() .
.
Решение
Поделив обе части уравнения на произведение ![]() ,
,
получим уравнение с разделенными переменными
![]() ,
,
откуда находим общий интеграл
![]() .
.
Следовательно, 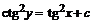 .
.
№ 000 [5]. Решить дифференциальное уравнение
![]() .
.
Решение
Раскрывая скобки и группируя произведения, содержащие производную, получим ![]() . Выразим производную через дифференциалы переменных
. Выразим производную через дифференциалы переменных ![]() , умножим обе части урав-
, умножим обе части урав-
нения на ![]() и разделим на произведение
и разделим на произведение 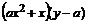 , тогда
, тогда ![]() . Интегрируя, получим
. Интегрируя, получим 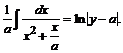 Выделяя из квадратного двучлена полный квадрат
Выделяя из квадратного двучлена полный квадрат 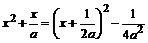 , записывая
, записывая ![]() вместо
вместо ![]() и интегрируя, получим:
и интегрируя, получим:
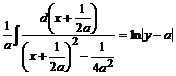 .
.
Откуда
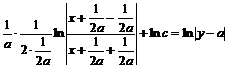 ,
,
причем для удобства дальнейших преобразований в качестве произвольного постоянного выбрано ![]() . Потенцируя, получим
. Потенцируя, получим 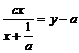 , следовательно, общее решение
, следовательно, общее решение ![]() , где
, где ![]() .
.
№ 000 [5]. Проинтегрировать дифференциальное уравнение ![]() .
.
Решение
Разрешим уравнение относительно производной 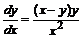 и выполним справа почленное деление
и выполним справа почленное деление ![]() . Осуществим замену
. Осуществим замену ![]() , тогда
, тогда ![]() , а
, а ![]() . Уравнение преобразует-
. Уравнение преобразует-
ся к виду ![]() , откуда
, откуда ![]() . Интегрируя, имеем
. Интегрируя, имеем 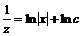 . Исключая вспомогательную переменную
. Исключая вспомогательную переменную ![]() , получим
, получим ![]() . Следовательно, искомое общее решение
. Следовательно, искомое общее решение 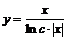 .
.
№ 000 [4]. Найти общий интеграл дифференциального уравнения
![]()
Решение
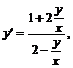 введем замену
введем замену ![]()
![]()
![]()
![]()
2.10.3 Задачи для самостоятельного решения
Выполнить задания № 000, 2748–2750, 2771–2774 [5].
2.10.4 Домашнее задание
1. Изучить теоретический материал по теме «Уравнения, приводящиеся к однородным. Уравнения в полных дифференциалах».
2. Выполнить задания № 000, 2744, 2747, 2768, 2769 [5].
2.11 Практическое занятие № 14. Уравнения, приводящиеся
к однородным. Уравнения в полных дифференциалах
2.11.1 Теоретические сведения и методические рекомендации
по решению задач
Рассмотрим уравнение вида
![]() .
.
Если ![]() , то уравнение однородное, так как
, то уравнение однородное, так как
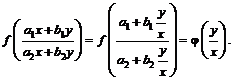
Если отлично от нуля по крайней мере одно из чисел ![]() или
или ![]() , то преобразование проводят с помощью замены
, то преобразование проводят с помощью замены 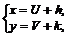
где ![]() и
и ![]() – новые переменные, а
– новые переменные, а ![]() и
и ![]() – постоянные величины преобразования. Так как
– постоянные величины преобразования. Так как ![]() , а
, а ![]() , то уравнение примет вид
, то уравнение примет вид
![]() .
.
Постоянные ![]() и
и ![]() определим из системы
определим из системы ![]()
а однородное уравнение ![]() преобразуем к стандартному виду
преобразуем к стандартному виду 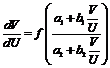 .
.
Если главный определитель системы 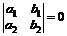 , то коэффициенты при х и y в равенстве пропорциональны, правая часть имеет вид
, то коэффициенты при х и y в равенстве пропорциональны, правая часть имеет вид
![]() .
.
Уравнение 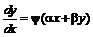 приводится к уравнению с разделя-ющимися переменными с помощью замены
приводится к уравнению с разделя-ющимися переменными с помощью замены 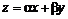 . Тогда
. Тогда ![]()
Подставляя, получим 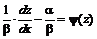 , или
, или
![]() .
.
Тогда ![]() , заменим переменную
, заменим переменную ![]() через
через ![]() , получим общий интеграл уравнения.
, получим общий интеграл уравнения.
Определение. Уравнение вида
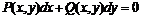
называется уравнением в полных дифференциалах, если его левая часть является полным дифференциалом некоторой функции ![]() , то есть
, то есть
![]()
Для того чтобы уравнение было в полных дифференциалах, необходимо и достаточно выполнение условия
![]() .
.
В этом случае ![]() есть общий интеграл уравнения. Функция
есть общий интеграл уравнения. Функция ![]() может быть найдена из системы уравнений
может быть найдена из системы уравнений
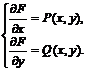
Все функции, удовлетворяющие первому уравнению системы, выражаются формулой
![]() ,
,
где ![]() – произвольная функция аргумента y, не зависящая от
– произвольная функция аргумента y, не зависящая от ![]() .
.
Определим величину ![]() так, чтобы функция
так, чтобы функция ![]() удов-
удов-
летворяла и второму уравнению системы. С этой целью равен-
ство ![]() дифференцируем по аргументу
дифференцируем по аргументу ![]()
![]() , приравниваем эту частную производную к функции
, приравниваем эту частную производную к функции ![]() и из полученного уравнения
и из полученного уравнения ![]()
![]() находим производную
находим производную ![]() . Интегрируя, определим величину
. Интегрируя, определим величину ![]() . Подставив ее в равенство
. Подставив ее в равенство ![]() , получим искомую функцию.
, получим искомую функцию.
2.11.2 Примеры решения задач
№ 000 [4]. Решить уравнение 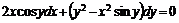 .
.
Решение
![]()
![]() , то есть
, то есть ![]() – данное урав-нение есть уравнение в полных дифференциалах.
– данное урав-нение есть уравнение в полных дифференциалах.
![]() . Для определения функ-ции
. Для определения функ-ции ![]() находим производную
находим производную ![]() , приравниваем
, приравниваем
ее к функции 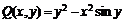 и из полученного уравнения
и из полученного уравнения ![]() находим
находим ![]() . Интегрируя, получим
. Интегрируя, получим ![]() , следовательно,
, следовательно, 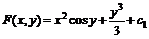 , а общий интеграл данного уравнения
, а общий интеграл данного уравнения ![]() , или
, или ![]() . Обозначим
. Обозначим ![]() , тогда общий интеграл уравнения определяется соотношением
, тогда общий интеграл уравнения определяется соотношением ![]() , где
, где ![]() – произвольная постоянная.
– произвольная постоянная.
№ 000 [4]. Найти общий интеграл дифференциального уравнения
![]()
Решение

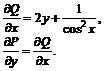
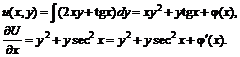
![]()
№ 000 [4]. Решить уравнение 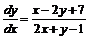 .
.
Решение
Так как ![]() , осуществим замену
, осуществим замену ![]()
Из системы ![]()
определим ![]() . Поэтому
. Поэтому ![]() ,
, ![]() , откуда
, откуда ![]() ,
, ![]() . Подставляя в исходное уравнение, получим
. Подставляя в исходное уравнение, получим 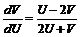 , или
, или 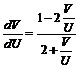 . Используя замену
. Используя замену ![]() , полу-
, полу-
чим ![]() , или
, или ![]() , а после разделения
, а после разделения
переменных ![]() =>
=> ![]() , тогда
, тогда ![]() . Потенцируя, найдем
. Потенцируя, найдем 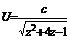 , следовательно,
, следовательно, ![]() . Так как
. Так как ![]() , то
, то ![]() , или
, или ![]() . Осуществим обратную замену
. Осуществим обратную замену 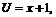
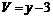 , получим общий интеграл исходного уравнения
, получим общий интеграл исходного уравнения ![]() . После упрощений окончательно
. После упрощений окончательно 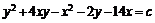 .
.
№ 000 [4]. Решить уравнение
![]() .
.
Решение
Так как коэффициенты при переменных ![]() и
и ![]() в выражениях
в выражениях ![]() и
и ![]() пропорциональны, то воспользуемся подстановкой
пропорциональны, то воспользуемся подстановкой 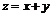 . Отсюда имеем
. Отсюда имеем ![]() , подставляя в уравнение, получим:
, подставляя в уравнение, получим:
![]() , или
, или ![]() .
.
Разделяя переменные, интегрируем 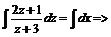
![]()
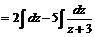 ;
; 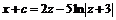 . Заменив в этом равенстве функцию
. Заменив в этом равенстве функцию ![]() через
через ![]() , получим общий интеграл исходного уравнения
, получим общий интеграл исходного уравнения 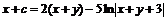 , или
, или ![]() .
.
2.11.3 Задачи для самостоятельного решения
Выполнить задания № 000, 2777, 2802, 2804 [5].
2.11.4 Домашнее задание
1. Изучить теоретический материал по теме «Интегрирование линейных уравнений. Метод вариации произвольной постоянной».
2. Выполнить задания № 000, 2803, 2805, 2806 [ 5].
2.12 Практическое занятие № 15. Интегрирование линейных уравнений. Метод вариации произвольной постоянной
2.12.1 Теоретические сведения и методические рекомендации по решению задач
Определение. Уравнение вида ![]() , где
, где ![]() и
и![]() – непрерывные функции, называется линейным дифференциальным уравнением первого порядка.
– непрерывные функции, называется линейным дифференциальным уравнением первого порядка.
Если ![]() , то данное уравнение называется линейным однородным уравнением, при
, то данное уравнение называется линейным однородным уравнением, при ![]() уравнение
уравнение ![]() – линейное неоднородное.
– линейное неоднородное.
Для нахождения общего решения данного уравнения применим метод вариации постоянной.
Найдем на первом этапе общее решение линейного однородного уравнения ![]() , соответствующего исходному неоднородному. Разделяя переменные и интегрируя, получим
, соответствующего исходному неоднородному. Разделяя переменные и интегрируя, получим ![]() ,
, ![]() . Потенцируя, находим общее решение однородного уравнения
. Потенцируя, находим общее решение однородного уравнения ![]() .
.
На втором этапе найдем общее решение исходного уравнения, считая ![]() функцией аргумента
функцией аргумента ![]() . Для определения величины
. Для определения величины ![]() подставим
подставим ![]() в исходное уравнение. Получим
в исходное уравнение. Получим 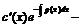
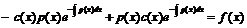 , или
, или ![]() .
.
Интегрируя, находим 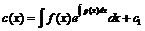 . Подставляя найденное выражение в
. Подставляя найденное выражение в ![]() , получим общее решение исходного линейного уравнения
, получим общее решение исходного линейного уравнения
![]() .
.
Для решения линейного неоднородного уравнения можно также использовать метод Бернулли. Искомую функцию ![]() определим как произведение
определим как произведение ![]() , тогда
, тогда ![]() . Подставляя
. Подставляя ![]() и
и ![]() в исходное уравнение, получим
в исходное уравнение, получим 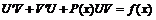 , или
, или ![]() . В качестве
. В качестве ![]() выберем такую функцию, для которой выражение, заключенное в квадратные скобки, равно
выберем такую функцию, для которой выражение, заключенное в квадратные скобки, равно
нулю. Тогда в равенстве 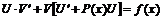 возможно
возможно
разделение переменных. Разрешим относительно ![]() равенство
равенство ![]() ,
, ![]() , или
, или ![]() . Тогда полу-
. Тогда полу-
чим уравнение для искомой функции ![]() :
: 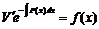 , или
, или ![]() , откуда
, откуда ![]() . Следовательно, общее решение исходного уравнения определится равенством
. Следовательно, общее решение исходного уравнения определится равенством
![]() .
.
2.12.2 Примеры решения задач
№ 000 [5]. Найти общий интеграл уравнения ![]() .
.
Решение
Применим метод вариации, для этого разрешим однородное уравнение ![]() . Разделив переменные, получим
. Разделив переменные, получим 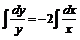 ,
,  . Потенцируя, выразим общее решение однородного уравнения
. Потенцируя, выразим общее решение однородного уравнения ![]() . Дифференцируя, находим
. Дифференцируя, находим ![]() . Подставляя в исходное уравнение
. Подставляя в исходное уравнение ![]() и
и ![]() , получим
, получим ![]() , или
, или ![]() , откуда
, откуда ![]() . Следовательно, общее решение имеет вид
. Следовательно, общее решение имеет вид 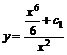 , или
, или ![]() .
.
№ 000 [5]. Найти частное решение уравнения
![]() , удовлетворяющее начальному условию
, удовлетворяющее начальному условию ![]() при
при ![]() .
.
Решение
Используя метод Бернулли, найдем общее решение ![]() в два этапа.
в два этапа.
![]() , откуда:
, откуда:
а)![]() ,
,
тогда ![]() , или
, или ![]() ;
;
б)![]() , откуда
, откуда ![]() . Осуществим замену
. Осуществим замену ![]() , тогда
, тогда ![]() .
.
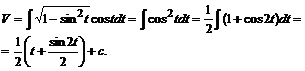
Возвращаясь к переменной ![]() , получим
, получим ![]() , в результате общее решение
, в результате общее решение 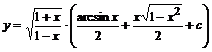 .
.
Используя начальное условие, определим значение ![]() :
:
![]() .
.
Частное решение имеет вид 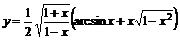 .
.
№ 000 [4]. Найти частное решение уравнения 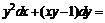 0,
0,
удовлетворяющее начальному условию 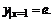
Решение
![]()
Пусть ![]()
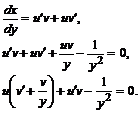
Разделим переменные в этом дифференциальном уравнении относительно функции ![]() , находим:
, находим:
1) 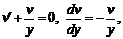
![]()
2) ![]()
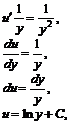
![]() – общее решение.
– общее решение.
![]()
![]() – частное решение.
– частное решение.
2.12.3 Задачи для самостоятельного решения
Выполнить задания № 000, 2787, 2789, 2792, 2837, 2854 [5].
2.12.4 Домашнее задание
1. Изучить теоретический материал по теме «Уравнения второго порядка и их решение путем понижения степени».
2. Выполнить задания № 000, 2791, 2793, 2836 [5].
2.13 Практическое занятие № 16. Уравнения второго порядка и их решение путем понижения степени
2.13.1 Теоретические сведения и методические рекомендации
по решению задач
Определение. Уравнение вида 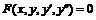 , где
, где ![]() – независимая переменная,
– независимая переменная, ![]() – искомая функция,
– искомая функция, ![]() и
и ![]() – ее производные, называется дифференциальным уравнением второго порядка.
– ее производные, называется дифференциальным уравнением второго порядка.
Если уравнение представимо в виде 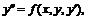 то его называют разрешенным относительно второй производной.
то его называют разрешенным относительно второй производной.
Отметим три частных вида уравнения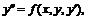 в которых решение его с помощью замены переменной сводится к решению уравнения первого порядка. Такое преобразование уравнения называется понижением порядка:
в которых решение его с помощью замены переменной сводится к решению уравнения первого порядка. Такое преобразование уравнения называется понижением порядка:
а) уравнение вида 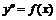 . Так как уравнение не содержит функций
. Так как уравнение не содержит функций ![]() и
и ![]() , воспользуемся заменой
, воспользуемся заменой ![]() , тогда
, тогда ![]() . Уравнение примет вид
. Уравнение примет вид 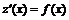 . Решая его, находим
. Решая его, находим ![]() . Так как
. Так как ![]() ,
, ![]() . Интегрируя повторно, получим искомое решение
. Интегрируя повторно, получим искомое решение 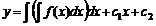 , где
, где ![]() и
и ![]() – произвольные постоянные;
– произвольные постоянные;
б) уравнение вида 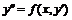 . Так как уравнение не содержит искомую функцию
. Так как уравнение не содержит искомую функцию ![]() , то воспользуемся, как и в предыдущем случае, заменой
, то воспользуемся, как и в предыдущем случае, заменой ![]() , тогда
, тогда ![]() . Уравнение преобразуется следующим образом:
. Уравнение преобразуется следующим образом: 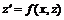 . Решив его, находим
. Решив его, находим ![]() . Так как
. Так как ![]() ,
, ![]() . Отсюда, интегрируя повторно, получим искомое решение
. Отсюда, интегрируя повторно, получим искомое решение ![]() , где
, где ![]() и
и ![]() – произвольные постоянные;
– произвольные постоянные;
в) уравнение вида 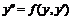 . Уравнение не содержит переменную
. Уравнение не содержит переменную ![]() , поэтому понижение порядка осуществим с помощью замены
, поэтому понижение порядка осуществим с помощью замены ![]() . По правилу дифференцирования сложной функции найдем
. По правилу дифференцирования сложной функции найдем
![]() .
.
Подставим ![]() и
и ![]() в уравнение, получим
в уравнение, получим ![]() . Решив его, находим
. Решив его, находим ![]() . Так как
. Так как ![]() ,
, ![]() . Отсюда
. Отсюда ![]() . Интегрируя, найдем общее решение данного уравнения
. Интегрируя, найдем общее решение данного уравнения 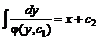 , где
, где ![]() и
и ![]() – произвольные постоянные.
– произвольные постоянные.
2.13.2 Примеры решения задач
№ 000 [5]. Решить уравнение ![]() .
.
Решение
Так как уравнение не содержит функций ![]() и
и ![]() воспользуемся заменой
воспользуемся заменой ![]() , тогда
, тогда ![]() . Уравнение примет вид
. Уравнение примет вид ![]() , следовательно,
, следовательно, ![]() . После замены
. После замены ![]() имеем
имеем ![]()
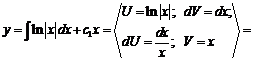
![]()

|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 |





