Математика в четырёх частях. Часть вторая. Неопределенный и определенный интегралы. Дифференциальное исчисление функции двух переменных. Дифференциальные уравнения. Двойные и тройные интегралы (стр. 3 )

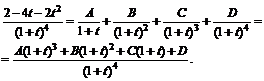
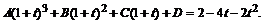
Имеем

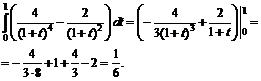
№ 000 [4]. Вычислить определенный интеграл

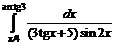
Решение

.

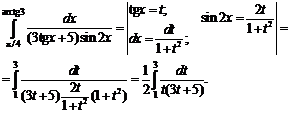
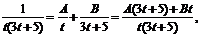
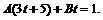
Имеем

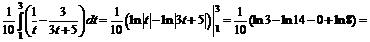
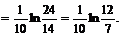
№ 000 [4]. Вычислить определенный интеграл .

Решение

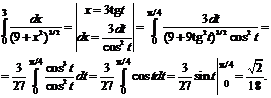
№ 000 [4]. Вычислить определенный интеграл

Решение

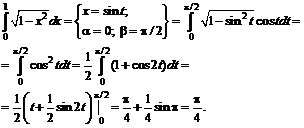
№ 000 [4]. Исследовать на сходимость

Решение

Так как предел не существует, то несобственный интеграл расходится.

№ 000 [4]. Исследовать на сходимость .

Решение

– интеграл схо-дится.

№ 000 [4]. Исследовать на сходимость .

Решение

Точка является особой точкой, так как подынтегральная функция имеет в ней бесконечный разрыв. Поэтому

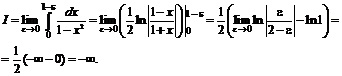
Так как предел бесконечный, то данный интеграл расходится.

№ 000 [4]. Задано комплексное число . Найти алгебраическую, тригонометрическую и показательную формы записи.

Решить уравнение .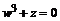

Решение

1) Домножим числитель и знаменатель на сопряженное знаменателю комплексное число и проведем алгебраические преобразования

– алгебраическая форма.

Модуль числа .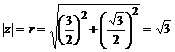

Аргумент находится в первой четверти

.

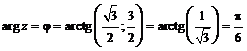Тригонометрическая форма числа

.

Показательная форма числа

.

2) для решения уравнения 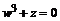необходимо выписать три значения корня кубического из числа.

.

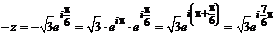Полученный аргумент числа не является главным значением, поэтому, пользуясь периодичностью функций и , можем перейти к другому аргументу, удовлетворяющему условию .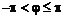

;

.

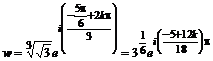Три решения исходного уравнения получаются при k = 0, 1, 2:

.

Выписанный аргумент не является главным значением аргумента (больше ), поэтому форму числа необходимо преобразовать: .

№ 000 [4]. Найти все значения корня .

Решение

.

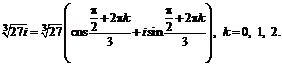
№ 000 [4]. Найти .

Решение

.

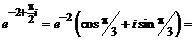
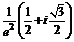2.5.3 Задачи для самостоятельного решения

Выполнить задания № 000, 1524, 1528, 1539, 1589, 1599–1601, 1547–1549, 1553, 1563, 1566, 1573 [5].

2.5.4 Домашнее задание

1. Подготовиться к контрольной работе.

2. Выполнить задания № 000, 1557, 1559, 1562 [5].

2.6 Практическое занятие № 8. Контрольная работа по теме «Интегралы»

Изучить теоретический материал по теме «Вычисление площа-
дей в декартовых и полярных координатах. Вычисление длин дуг.
Вычисление объемов тел, площадей поверхностей вращения, приложения к механике».

2.7 Практическое занятие № 9. Вычисление площадей
в декартовых и полярных координатах. Вычисление длин дуг. Вычисление объемов тел, площадей поверхностей
вращения, приложения к механике

2.7.1 Теоретические сведения и методические рекомендации
по решению задач

Определенный интеграл на отрезке представляет собой площадь криволинейной трапеции, ограниченной графиком функции f(x). Если график расположен ниже оси Ох, т. е. f(x) < 0, то площадь имеет знак
«-», если график расположен выше оси Ох, т. е. f(x) > 0, то площадь имеет знак «+».

Для нахождения суммарной площади используется формула . Площадь криволинейного сектора может быть найдена по формуле .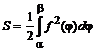

Вычисление длины дуги кривой в декартовых координатах осуществляется по формуле .

Если уравнение кривой задано параметрически, то получаем

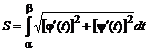, где х = j(t) и у = y(t).

Если задана пространственная кривая х = j(t), у = y(t) и z =Z(t),

то .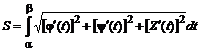

Если кривая задана в полярных координатах, то

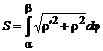, r = f(j).

Пусть имеется тело, у которого площадь любого поперечного сечения известна как непрерывная функция Q = Q(x), тогда объем может быть найден по формуле

.

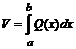Объем тела, полученного вращением дуги кривой вокруг оси абсцисс, определяется формулой:

.

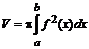Формула для вычисления площади поверхности тела вращения

.

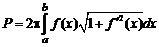2.7.2 Примеры решения задач

№ 000 [4]. Вычислить площадь фигуры, ограниченной графиками функций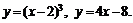

Решение

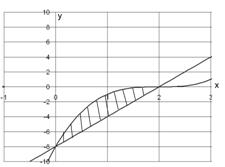
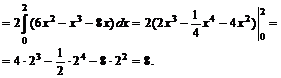
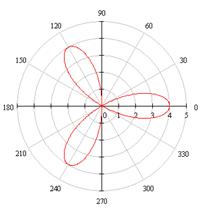
№ 000 [4]. Вычислить площадь фигуры, ограниченной линиями, заданными уравнениями в полярных координатах

Решение

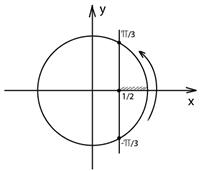
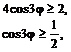
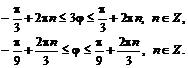
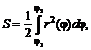
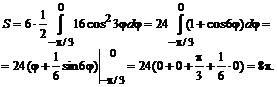
№ 000 [4]. Вычислить длину дуги кривой, заданной параметрическими уравнениями

Решение

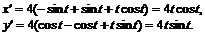
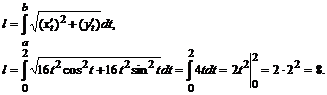
№ 000 [4]. Вычислить длину дуги кривой, заданной уравнениями в полярных координатах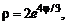

Решение

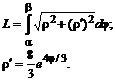
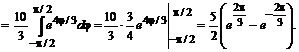
№ 000 [4]. Вычислить объем тела, образованного вращением фигур, ограниченных графиками функций, относительно оси вращения :

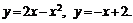
Решение

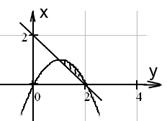
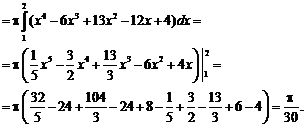
2.7.3 Задачи для самостоятельного решения

Выполнить задания № 000, 1669, 1672, 1677, 1680, 1684, 1626, 1633–1637, 1685, 1687, 1717 [5].

2.7.4 Домашнее задание

1.  Подготовиться к защите типового расчета.

2.  Выполнить задания № 000, 1672, 1628, 1651, 1655, 1661, 1687, 1690, 1715 [5].

2.8 Практические занятия № 10–11. Частные производные функций нескольких переменных. Градиент и производная
по направлению вектора. Уравнение касательной плоскости и нормали к поверхности

2.8.1 Теоретические сведения и методические рекомендации
по решению задач

Определение. Если каждой паре независимых друг от друга чисел (х, у) из некоторого множества по какому-либо правилу ставится в соответствие одно или несколько значений переменной z, то переменная z называется функцией двух переменных z = f(x, y).

Определение.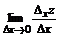 называется частной производной функции z = f(x, y) по х, где .

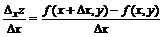Аналогично определяется частная производная функции по у

.

Определение. Полным дифференциалом функции z = f(x, y) называется главная линейная часть приращения функции Dz в точке (х, у) .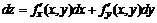

Для функции произвольного числа переменных

.

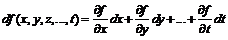Если поверхность задана уравнением z = f(x, y), где f(x, y) – функция, дифференцируемая в точке М0(х0, у0), то касательная плоскость в точке N0(x0, y0,(x0, y0)) существует и определяется уравнением

.

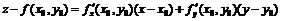Уравнение нормали к поверхности в этой точке

.

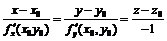Производные от и называются частными производными второго порядка

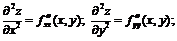
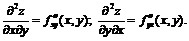
Продолжая дифференцировать полученные равенства, получим частные производные более высоких порядков.

Определение. Частные производные вида

и т. д. называются смешанными производными.

Теорема. Если функция f(x, y) и ее частные производные определены и непрерывны в точке М(х, у) и ее окрестности, то верно соотношение , т. е. частные производные высших порядков не зависят от порядка дифференцирования.

Аналогично определяются дифференциалы высших порядков

.

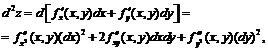
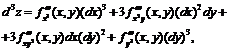
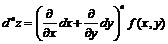Определение. Предел 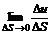называется производной функции u(x, y, z) по направлению вектора в точке с координатами ( x, y, z)

.

Определение. Градиентом функции u называется вектор

.

Направление градиента есть направление наиболее быстрого роста функции. С точки зрения геометрического представления, градиент перпендикулярен поверхности уровня функции.

2.8.2 Примеры решения задач

№ 000 [4]. Найти полный дифференциал функции .

Решение

.

№ 000 [4]. Найти уравнения касательной плоскости и нормали к поверхности 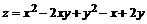в точке М(1, 1, 1).

Решение

;

Уравнение касательной плоскости

Уравнение нормали .

№ 000 [4]. Вычислить производную функции z = x2 + y2x в точке А(1, 2) по направлению вектора , если В(3, 0).

Решение

Определим координаты вектора : = (3-1; 0-2) = (2; -2) =

= 2. =.

Находим частные производные функции z в общем виде

Значения этих величин в точке А :

Для нахождения направляющих косинусов вектора производим следующие преобразования:

= ;

cosa = ; cosb = -.

Окончательно получаем – значение производной заданной функции по направлению вектора .

№ 000 [4]. Дана функция .

Найти:

1) в точке;

2) производную по направлению вектора от точки к точке.

Решение

Найдем значения частных производных в точке

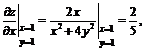
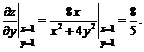
Подставив найденные значения частных производных в выражение градиента, получим .

Определим единичный вектор, в направлении которого вычисляется производная

.

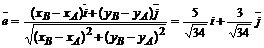Искомая производная по направлению

.

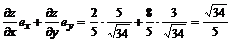2.8.3 Задачи для самостоятельного решения

Выполнить задания № 000, 1802, 1822, 1823, 1848, 1876–1878, 1885, 1887 [5].

2.8.4 Домашнее задание

1. Изучить теоретический материал по теме «Абсолютный экстремум. Условный экстремум функции двух переменных. Наиболь-
шее и наименьшее значения функции, заданной в области и на гра-нице».

2. Выполнить задания № 000–1811, 1814, 1864, 1865, 1879,
1889 [5].

2.9 Практическое занятие № 12. Абсолютный экстремум. Условный экстремум функции двух переменных.

Наибольшее и наименьшее значения функции, заданной

в области и на границе

2.9.1 Теоретические сведения и методические рекомендации
по решению задач

Определение. Если для функции z = f(x, y) в некоторой окрестности точки М0(х0, у0) верно неравенство 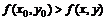, то точка М0 называется точкой максимума.

Определение. Если для функции z = f(x, y) в некоторой окрестности точки М0(х0, у0) верно неравенство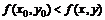, то точка М0 называется точкой минимума.

Если функция f(x, y) в точке (х0, у0) имеет экстремум, то в этой точке либо обе ее частные производные первого порядка равны нулю , либо хотя бы одна из них не существует. Эту точку (х0, у0) называют критической точкой.

Пусть в окрестности критической точки (х0, у0) функция f(x, y) имеет непрерывные частные производные до второго порядка включительно. Рассмотрим выражение

.

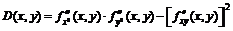1)  Если D(x0, y0) > 0, то в точке (х0, у0) функция f(x, y) имеет экстремум, причем при – максимум, при 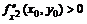– минимум.

2)  Если D(x0, y0) < 0, то в точке (х0, у0) функция f(x, y) не имеет экстремума.

В случае, если D = 0, то вывод о наличии экстремума сделать нельзя.

Если переменные х и у, входящие в функцию u = f( x, y), не являются независимыми, т. е. существует некоторое соотношение j(х, у)=0, которое называется уравнением связи, то находят условный экстремум.

С учетом уравнения связи имеем: u = f(x, y(x)). В точках экстремума

=0, .

Следовательно,

,

или .

Для выполнения этого условия во всех точках найдем неопределенный коэффициент l так, чтобы выполнялась система трех уравнений

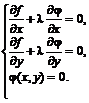
2.9.2 Примеры решения задач

№ 000 [4]. Найти наибольшее и наименьшее значения функции в замкнутом треугольнике, ограниченном осями координат и прямой .

Решение

Для нахождения стационарных значений приравниваем нулю частные производные

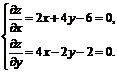
Откуда .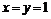

Значение функции в найденной стационарной точке .

Рассмотрим значения функции на границе области.

Границу области составляют:

1)  отрезок оси Ox, определяемый неравенствами ;

2)  отрезок оси Oy, определяемый неравенствами ;

3)  отрезок прямой , определяемый неравенствами . На первом из этих отрезков , а следовательно, .

Для нахождения экстремальных значений функции на этом промежутке рассмотрим уравнение 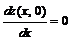, откуда . Функция непрерывна на замкнутом интервале . Поэтому она должна принимать на нем свои наибольшее и наименьшее значения. Эти значения она может принимать внутри интервала (в точках стационарности) или на границах. Внутри интервала, то есть при , функция не имеет экстремумов. Поэтому остается рассмотреть значения z(0, 0)=0, z(3, 0)= -9.

Первое оказывается наибольшим, второе – наименьшим. На
отрезке оси Oy: 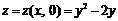. Корень уравнения 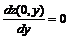, значение , лежит вне рассматриваемого интервала; внутри интервала нет точек стационарности функции .

Остается рассмотреть значения , .

Первое дает нам наибольшее, второе – наименьшее значения функции на замкнутом интервале 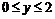. На отрезке прямой 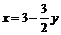функция 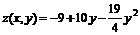и 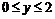. Корнем уравнения является значение . При рассматриваемая функция имеет значение, равное . Далее, , .

Таким образом, значение является наибольшим на данной прямой, значение – наименьшим.

Сравнивая значения на сторонах треугольника и в точке (1, 1), приходим к выводу, что свое наибольшее значение в данном замкнутом треугольнике функция принимает в точке (0, 0), а наименьшее – в точке (3, 0), при этом , .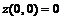

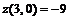№ 000 [4]. Найти экстремум функции f(x, y) = xy, если уравнение связи 2x + 3y – 5 = 0.

Решение

,

.

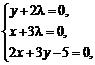
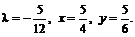
Следовательно, М – точка возможного экстремума.

Из условия связи 2dx+3dy =0, dx= -1,5dy, тогда следовательно, М – точка условного максимума, f(.

2.9.3 Задачи для самостоятельного решения

Выполнить задания № 000, 2006, 2009, 2012, 2021–2023 [5].

2.9.4 Домашнее задание

1. Изучить теоретический материал по теме «Уравнения с разделяющимися переменными, одно­родные уравнения».

2. Выполнить задания № 000, 2010, 2011, 2031, 2039 [5].

2.10 Практическое занятие № 13. Уравнения
с разделяющимися переменными, одно­родные уравнения

2.10.1 Теоретические сведения и методические рекомендации
по решению задач

Общий вид дифференциального уравнения первого порядка определяется равенством: . Если данное уравнение представимо в виде 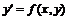, то его называют разрешенным относительно производной.

Если , то уравнение называют уравнением с разделяющимися переменными.

Преобразуем 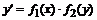следующим образом:

,

откуда, интегрируя, получим:

.

Определение. Функция называется однородной функцией n-го измерения относительно переменных и , если при любом значении справедливо тождество

.

Определение. Уравнение первого порядка называется однородным относительно и , если функция есть однородная функция нулевого измерения относительно и .

Утверждение. Если есть однородная функция нулевой степени, то она зависит только от отношения переменных и .

На основании утверждения уравнение 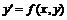преобразуется к виду .

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5