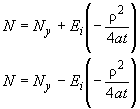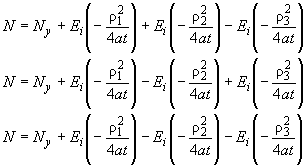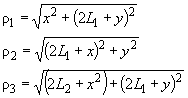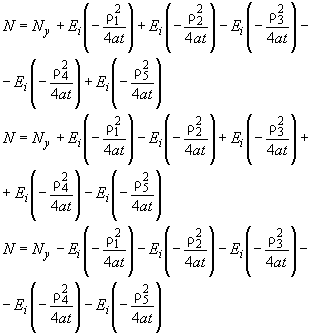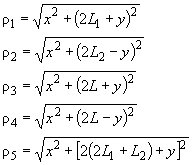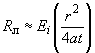 ,
,
где ![]() - расстояние точки от центра ряда, равное
- расстояние точки от центра ряда, равное
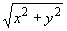 .
.
При наличии двух и более рядов скважин расчет их взаимодействия производится с использованием тех же зависимостей, что и для одного ряда. При определении понижения в какой-либо точке ![]() (
(![]() ) определяется влияние на эту точку каждого ряда в отдельности и полная напорная функция
) определяется влияние на эту точку каждого ряда в отдельности и полная напорная функция ![]() находится как сумма напорных функций всех рядов
находится как сумма напорных функций всех рядов
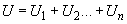 .
.
2.2. Кольцевая система скважин
Скважины, располагаемые по замкнутому контуру (рис. П.1.5) с расходом каждой из них ![]() и суммарным расходом всех скважин
и суммарным расходом всех скважин ![]() , для расчета
, для расчета ![]() используются следующие формулы:
используются следующие формулы:
- при расположении скважин в плане по неправильному многоугольнику (по Форхгеймеру):
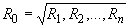 ,
,
где ![]() - число вершин многоугольника;
- число вершин многоугольника; ![]() - расстояние от вершин многоугольника до центра его тяжести;
- расстояние от вершин многоугольника до центра его тяжести;
- при расположении скважин по контуру, близкому к кругу:
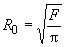 ;
;
- при расположении скважин в системе, имеющей в плане вид четырехугольника при ![]() >3,
>3, 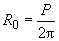 ,
,
где ![]() - длина четырехугольника;
- длина четырехугольника; ![]() - ширина;
- ширина; ![]() - периметр.
- периметр.
При ![]() >6
>6![]() 8 короткие ряды скважин можно не учитывать и установку рассчитывать как линейную.
8 короткие ряды скважин можно не учитывать и установку рассчитывать как линейную.
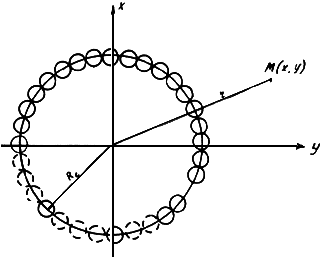
Рис. П.1.5. Схема кольцевой системы скважин
Значения гидравлического сопротивления для кольцевой системы ![]() даны на графике (рис. П.1.6) в зависимости от
даны на графике (рис. П.1.6) в зависимости от ![]() и
и ![]() , где
, где ![]() и
и 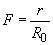 .
.

Рис. П.1.6. График функции ![]()
В начальные моменты времени (при ![]() или
или ![]() ) минимальные значения
) минимальные значения ![]() имеет точка в центре кольцевой системы (
имеет точка в центре кольцевой системы (![]() = 0), для которой
= 0), для которой ![]() .
.
При ![]() >3,5 понижения уровня во всех точках внутри кольца выравниваются.
>3,5 понижения уровня во всех точках внутри кольца выравниваются.
Для расчета понижения уровня в точке вне кольца на расстоянии ![]() при
при ![]() >2 можно пользоваться формулой
>2 можно пользоваться формулой
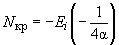 .
.
2.3. Площадная система скважин
Площадь, в пределах которой расположены скважины, для расчета можно представить в виде равновеликого круга радиусом ![]() (рис. П.1.7):
(рис. П.1.7):
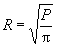 ,
,
где ![]() - действительная площадь участка, на котором расположены скважины.
- действительная площадь участка, на котором расположены скважины.
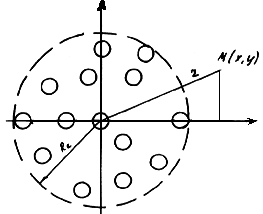
Рис. П.1.7. Схема обобщенной системы скважин на кривой площади
Гидравлическое сопротивление ![]() определяется по графику (рис. П.1.8) в зависимости от
определяется по графику (рис. П.1.8) в зависимости от ![]() и
и 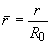 , где
, где
![]() .
.
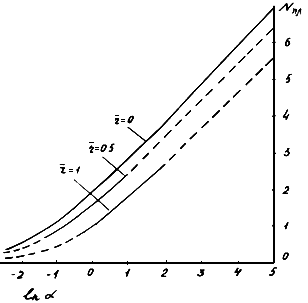
Рис. П.1.8. График функции ![]()
Для центра круга
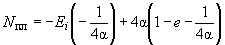 .
.
В центре круга при ![]() >2
>2![]() 2,5
2,5
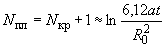 .
.
Как и в кольцевой системе, при ![]() >1,5
>1,5![]() 2 площадную систему можно заменить единичным колодцем с тем же суммарным расходом.
2 площадную систему можно заменить единичным колодцем с тем же суммарным расходом.
3. Системы скважин в ограниченных пластах
Для расчетов ограниченных в плане пластов используется метод зеркального отображения и наложения течений. Ниже приводятся формулы (табл. П.1.2) для ограниченных в плане пластов, изображенных на рис. П.1.9, П.1.10 и П.1.11.
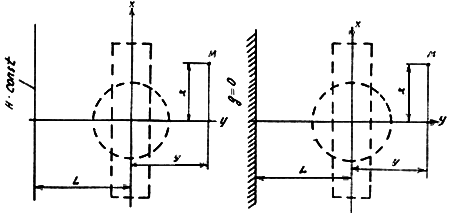
Рис. П.1.9. Схемы пластов, ограниченных контурами с одной стороны (полуограниченные пласты)
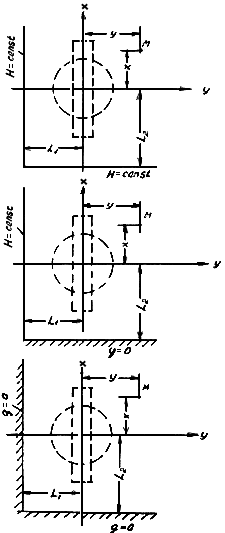
Рис. П.1.10. Схемы пластов, ограниченных двумя взаимно пересекающимися прямолинейными контурами
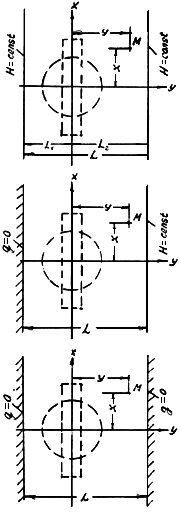
Рис. П.1.11. Схемы пластов, ограниченных двумя параллельными контурами
1.2. Формулы для ограниченных в плане пластов
N рис. | N для любой точки М (х, у) | | Радиусы-векторы для отображений ( | Приме - чания |
|
|
|
| |
|
|
|
| |
|
|
|
|
|
![]() - внешнее гидравлическое сопротивление для соответствующих схем при определении напорной функции в любой точке пласта;
- внешнее гидравлическое сопротивление для соответствующих схем при определении напорной функции в любой точке пласта; ![]() - гидравлическое сопротивление для обобщенной системы скважин в безграничном пласте: для линейной системы
- гидравлическое сопротивление для обобщенной системы скважин в безграничном пласте: для линейной системы ![]() , для кольцевой
, для кольцевой ![]() , для площадной системы
, для площадной системы ![]() .
.
4. Определение понижения уровней в скважинах
Внутреннее гидравлическое сопротивление в скважине ![]() , необходимое для определения понижения уровня внутри самой скважины, можно найти из следующей зависимости:
, необходимое для определения понижения уровня внутри самой скважины, можно найти из следующей зависимости:
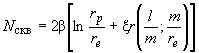 .
.
* где 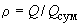 ;
; ![]() - расход данной скважины;
- расход данной скважины; ![]() - суммарный расход всех взаимодействующих скважин;
- суммарный расход всех взаимодействующих скважин; ![]() - радиус скважины;
- радиус скважины; ![]() - гидравлическое сопротивление, обусловленное несовершенством скважины по степени вскрытия и определяемое по табл. П.1.3 в зависимости от длины фильтра
- гидравлическое сопротивление, обусловленное несовершенством скважины по степени вскрытия и определяемое по табл. П.1.3 в зависимости от длины фильтра 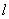 , мощности пласта
, мощности пласта ![]() и радиуса скважины
и радиуса скважины ![]() ; величины
; величины ![]() приведены в табл. П.1.3;
приведены в табл. П.1.3; ![]() - приведенный радиус условной области влияния данной скважины в условиях взаимодействия, определяемой в зависимости от схемы расположения скважин.
- приведенный радиус условной области влияния данной скважины в условиях взаимодействия, определяемой в зависимости от схемы расположения скважин.
____________
* Текст в соответствии с оригиналом. Примечание "КОДЕКС".
1.3
| Значения | |||||||||
| 0,5 | 1 | 3 | 10 | 30 | 100 | 200 | 500 | 1000 | 2000 |
0,05 | 0,00423 | 0,135 | 2,3 | 12,6 | 35,5 | 71,9 | 94 | 126 | 149 | 169 |
0,1 | 0,00391 | 0,122 | 2,04 | 10,4 | 24,5 | 43,5 | 54,9 | 70,2 | 81,8 | 93,5 |
0,3 | 0,00297 | 0,0908 | 1,29 | 4,79 | 9,2 | 14,3 | 17,7 | 21,8 | 24,9 | 28,2 |
0,5 | 0,00164 | 0,0494 | 0,656 | 2,26 | 4,21 | 6,5 | 7,86 | 9,64 | 11 | 12,4 |
0,7 | 0,000546 | 0,0167 | 0,237 | 0,879 | 1,69 | 2,67 | 3,24 | 4,01 | 4,58 | 5,19 |
0,9 | 0,0000482 | 0,0015 | 0,0251 | 0,128 | 0,302 | 0,537 | 0,677 | 0,867 | 1,01 | 1,15 |
Для линейной и кольцевой систем при одинаковых расстояниях между скважинами, равных 2![]() ,
,
![]() ,
,
а при разных расстояниях между скважинами 2![]() и 2
и 2![]() можно принимать
можно принимать
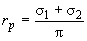 .
.
В случае площадного размещения скважин
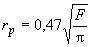 ,
,
где ![]() - площадь, приходящаяся на каждую скважину.
- площадь, приходящаяся на каждую скважину.
Для безнапорных потоков (по M.)
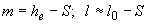 ,
,
где ![]() - полная мощность водоносного пласта (глубина статического уровня до водоупора);
- полная мощность водоносного пласта (глубина статического уровня до водоупора); ![]() - глубина погружения нижней кромки незатопленного фильтра под статический уровень грунтовых вод;
- глубина погружения нижней кромки незатопленного фильтра под статический уровень грунтовых вод; ![]() - понижение уровня в данной точке, полученное по расчету взаимодействующей системы скважин.
- понижение уровня в данной точке, полученное по расчету взаимодействующей системы скважин.
Для более строгого решения систем взаимодействующих скважин следует применять электронно-вычислительные машины.
Пример расчета водопонизительной линейной системы из 10 скважин приводится по Ф. M.Бочевер, M., 1963 г., с. 45.
В безнапорном потоке мощностью ![]() = 15 м закладывается водозабор из 10 скважин, располагающихся линейно (рис. П.1.12).
= 15 м закладывается водозабор из 10 скважин, располагающихся линейно (рис. П.1.12).
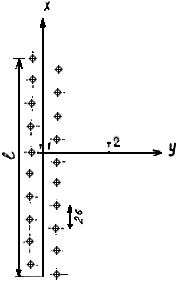
Рис. П.1.12. Схема линейного водозабора
Расход каждой скважины ![]() = 7 л/сек= 605 м
= 7 л/сек= 605 м![]() /сутки, общий расход всей системы
/сутки, общий расход всей системы ![]() =7·10= 70 л/сек=6050 м
=7·10= 70 л/сек=6050 м![]() /сут.
/сут.
Расстояния между скважинами 2![]() = 80 м.
= 80 м.
Общая длина ряда 2 = 2![]() = 10·80= 800 м.
= 10·80= 800 м.
Коэффициент фильтрации водоносного пласта ![]() = 30 м/сутки.
= 30 м/сутки.
Коэффициент водоотдачи ![]() = 0,22. Требуется определить
= 0,22. Требуется определить ![]() в центре ряда (на рис. П.1.12) и
в центре ряда (на рис. П.1.12) и ![]() на расстоянии 200 м (точка 2) в момент времени
на расстоянии 200 м (точка 2) в момент времени ![]() = 100 сут.,
= 100 сут., ![]() = 300 сут.,
= 300 сут., ![]() = 10000 сут.
= 10000 сут.
Решение.
Для расчета используются формулы:
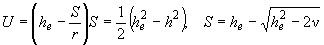 (1)
(1)![]() . (2)
. (2)
Гидравлическое сопротивление определяется по стандартным графикам.
1) Определяется коэффициент пьезопроводности по формуле:
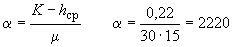 м
м![]() /сут.
/сут.
2) Безразмерные параметры при этом будут:
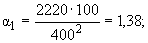
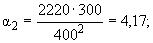
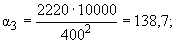
![]() и
и ![]() .
.
3) Для первого момента времени (![]() = 100 сут,
= 100 сут, ![]() = 1,38;
= 1,38; ![]() = 0,32) и точке 1 в центре ряда из графика находим
= 0,32) и точке 1 в центре ряда из графика находим ![]() = 3,2.
= 3,2.
4) по формуле (2)
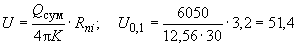 м
м![]() ,
,
откуда согласно формуле (1)
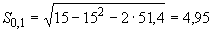 м.
м.
5) Таким путем сделаны расчеты для других значений ![]() (и соответственно
(и соответственно ![]() ) для точек 1 и 2. Результаты приводятся в табл. П.1.4.
) для точек 1 и 2. Результаты приводятся в табл. П.1.4.
1.4
|
|
|
|
|
|
|
| 100 | 1,38 | 0,32 | 3,2 | 51,4 | 4,95 |
0 | 300 | 4,17 | 1,43 | 4,27 | 68,4 | 6,61 |
| 10000 | 138,7 | 2,62 | 5,44 | 87,2 | 7,89 |
| 100 | 1,38 | 0,32 | 1,94 | 31,2 | 2,27 |
0,5 | 300 | 4,17 | 1,43 | 2,94 | 47,2 | 3,54 |
| 10000 | 138,7 | 2,62 | 4,13 | 66,3 | 4,28 |
6) Определяем понижение уровня непосредственно в скважине в последний момент времени ![]() = 10000 сут. Скважина совершенна (
= 10000 сут. Скважина совершенна (![]() =0), радиус ее
=0), радиус ее![]() = 0,15 м. По формуле (3)
= 0,15 м. По формуле (3)

|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 10 |