Рис.8.Направление потоков расплава в III зоне экструдера.

Прямой и обратный потоки по оси Z (вдоль витков шнека). Прямые и обратные потоки по оси X (между витками шнека).

С тепловой точки зрения в зоне дозирования идет диссипативное выделение тепла qд = η(γ’)2 (4.36)

(для степенной жидкости qд = К(γ’)n+1exp(E/RT)), перенос тепла вдоль оси z вместе с движущимся материалом

qz = ρСVМT (4.37)

и отвод тепла в стенки цилиндра и шнека

qц = qш = α (Т – Тц), (4.38) , где α ≈ mλ/H.

Тепловой баланс:

qzВН + qдВНdz = [qz +(dqz/dz)dz]BH + qцBdz + qшBdz . (4.39)

После сокращения и деления на ВНdz (элементарный объем параллелепипеда) получаем: dqz/dz = qд + (qц + qш)/Н. При подстановке в него расшифрованных значений q и γ’ = VМ/Н получаем: ρСVМdT/dz= К(γ’)n+1exp(E/RT)+2mλ (Т–Тц)/H2 (4.40)

При его решении с граничными условиями Тz=0 = T0 получаем:

T(z) = Tц + (kH2/2mλ)( VМ/Н)n+1exp(E/RTср) –

[kH2/2mλ)(VМ/Н)n+1exp(E/RTср)– T0 +Tц]exp(-2mλ/VМH2ρС). (4.41)

Главной неприятностью в этом уравнении является значение Tср, т. е. усредненная температура по потоку. Поэтому решение последнего уравнения возможно только численным методом итераций в предположении, что Tср = Тц или рассчитывая среднюю температуру.

Общее количество теплоты от внутреннего трения при экструзии расплава полимера составляет:

Σqд = K(8π3R3N2ηL/H + QP/cos2φ + 4π2R2N2ηeL/δtgφ), (4.42)

где P и Q – давление и расход при экструзии, η – вязкость расплава, R – радиус шнека, N – скорость его вращения, L – длина шнека, δ – зазор между гребнем и цилиндром, e – ширина гребня шнека. Таким образом, выделение тепла пропорционально N2, а отвод тепла (вместе с материалом) пропорционален N. Поэтому при высоких скоростях экструдер обязательно будет перегреваться.

ДВИЖЕНИЕ МАТЕРИАЛА В ГОЛОВКЕ ЭКСТРУДЕРА,

ЕЕ РАБОЧАЯ ХАРАКТЕРИСТИКА И РАБОЧАЯ ТОЧКА ЭКСТРУДЕРА

Рабочая характеристика головки для материала с ньютоновской вязкостью рассчитывается по простой формуле: Q=KDP/h, (4.43) , где DР - давление в головке. Для материала с неньютоновскими свойствами необходимо учитывать изменение вязкости в зависимости от скорости сдвига (пунктир).

Qэ Qг Q

1 2

 

2 1 3

экструдер головка

DP DP DP

Рис.9. Рабочие характеристики экструдера и головки для

ньютоновской (1) и неньютоновской (2) жидкостей. Рабочая точка (3).

Коэффициент геометрической формы головки - К зависит от её размеров и типа каналов, и коэффициентов геометрической формы головки (К1) с сетками (К2) и решёткой (К3). Он определяется сложением обратных значений К:

1/K = 1/K1 + 1/K2 + 1/K3 … (4.44)

Для цилиндрической головки К1 можно рассчитать по формуле: К1 =πd4/128 lгол .

Весь расплав полимера, вышедший из III зоны экструдера, должен пройти через головку. Расход материала через головку, таким образом, должен быть равен расходу, обеспечиваемому экструдером. На рис.9 это выражается пересечением рабочих характеристик экструдера и головки.

ОХЛАЖДЕНИЕ РАСПЛАВА ПОЛИМЕРА ПОСЛЕ ГОЛОВКИ.

При экструзии изделия (например, трубы) расплав полимера частично охлаждается в калибрующей насадке, а окончательно в ванне с водой. Поэтому с технической точки зрения общее время охлаждения будет зависеть от скорости движения трубы, полученной из расплава - vэкстр:

tохл = (Lкалибр + Lванны)/ vэкстр (4.45)

В этом случае скорость охлаждения можно рассчитать по уравнению нестационарной теплопроводности. При величине критерия Fo>0,1 число членов суммы можно ограничить только первым членом. Температура на внутренней поверхности трубы Т(t) не должна превышать Тпл полимера. Она рассчитывается как: [T(t) – Tc]/(Tp-Tc) = (4/π) exp(- π2Fo/4), (4.46)

где Тр – температура расплава, а Тс – температура наружной стенки трубы. Так как она обычно неизвестна, процесс теплообмена можно описать с учетом конвективной теплоотдачи, зная температуру охлаждающей жидкости Тохл. В целом, все это дает возможность рассчитать скорость экструзии:

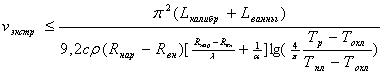(4.47)

где Rнар и Rвн – наружный и внутренний диаметры трубы, с и ρ –теплофизические свойства твердого полимера, α – коэффициент теплоотдачи [α= 9,74+0,07(Тр-Тохл)]. Более точно процесс охлаждения можно рассчитать, используя ЭВМ или номограммы для определения зависимости T(t) от Bi и Fo.

При получении рукавных пленок расплав полимера охлаждается на воздухе. Теплоту, необходимую для его охлаждения до линии кристаллизации – q1 можно рассчитать по уравнению: q1 = ρp.v[(Tp-Tпл)ср - Qпл], (4.48)

где v – объемная скорость подачи расплава, ρp и ср – его теплофизические свойства. Теплоту, необходимую для охлаждения рукава длиной L и радиусом Rср выше линии кристаллизации – q2 также можно рассчитать по уравнению теплоотдачи: q2 = 2πRср .α . L(Тср - Тохл), (4.49)_

где Тср = (Тпл+Тохл)/2, α – коэффициент теплоотдачи

(α = 3,3v возд 1,5), где v возд – скорость подачи воздуха, охлаждающего пленку. Тепло, затраченное на охлаждение пленки в целом равна: Qохл = 2сср ρсp πRср δ V (Tпл-Tохл), (4.50)

где V – линейная скорость пленки, сср и ρсp – ее средние теплофизические значения.

ЛИТЬЕ ПОД ДАВЛЕНИЕМ.

ОХЛАЖДЕНИЕ МАТЕРИАЛА В ФОРМЕ.

При переработке методом литья под давлением полимер расплавляют и под высоким давлением впрыскивают в закрытую охлаждаемую форму. Плавление гранул идет в материальном цилиндре за счет теплопередачи и диссипативного разогрева и температуру полимера в каждой зоне цилиндра можно рассчитать по формулам, приведенным выше. Время заполнения литьевой формы – tзап расплавом термопласта зависит от нескольких факторов и, в т. ч., от его вязкости и температуры, но поскольку расплав по мере заполнения формы остывает и его температура меняется от начальной Т0 до температуры прекращения текучести Ттек, то время заполнения приходится рассчитывать с учетом нестационарности процесса: tзап = 0,23(d2ср/a)lg[0,5+(Тр-Тс)/(Ттек-Тс)], (4.51)

где dср – размер минимального сечения формы, Тс – температура ее стенки, а – коэффициент температуропроводности расплава. Если речь идет о кристаллизующемся полимере, то в этом случае следует учитывать необходимость отвода скрытой теплоты плавления Qпл.

После заполнения формы стадия выдержки расплава под давлением продолжается до момента затвердевания расплава в литниковом канале. Это время рассчитывают также по формулам нестационарной теплопроводности:

tвпд = (клr2/5,76a) 2,3 lg[1,6(Тр-Тс)/(Ттек-Тс)], (4.52)

где r – радиус литника, кл – поправочный коэффициент фомы литника, а – коэффициент температуропроводности расплава. Охлаждение изделия, находящегося в форме, происходит кондуктивным путем и продолжается до необходимой жесткости. Время охлаждения tохл зависит, естественно, от геометрии изделия и рассчитывается по формулам: (4.53-4.55)

tохл =[2,3 δ2/ π2a] lg[(4/π)(Тр-Тс)/(Тизд-Тс)] для пластины

tохл = {2,3 r2/[a(5,76+2,46(R/L)]} lg[(2,04(Тр-Тс)/(Тизд-Тс)]

для цилиндра

tохл = [2,3 δ2B2L2/ π2a(δ2B2+ δ2L2+B2L2)] lg[(43/π3)(Тр-Тс)/(Тизд-Тс)] для параллелепипеда, где δ, R, L, B – толщина, радиус, длина и ширина изделия, Тизд – температура извлечения изделия (Тизд= Тстекл – 10-200). Для технологических расчетов из времени охлаждения вычитают время выдержки под давлением, тк. При выдержке также происходит охлаждение. В приведенные уравнения входит параметр Тс – температура стенки формы, постоянство которой обеспечивается мощной системой охлаждения форм.

Вышеуказанными формулами можно пользоваться и для расчета времени прогрева в форме литьевых автоматов для литья реактопластов. Для этого следует заменить приведенную температуру (Тр-Тс)/(Тизд-Тс) на комплекс

(Тс-Тр)/(Тс-Тцентр изд), где Тцентр изд - температура в центре изделия (Тс-Тцентр изд ) = 15-200.

ВАКУУМ-ФОРМОВАНИЕ.

ПРОГРЕВ И ОХЛАЖДЕНИЕ ИЗДЕЛИЙ.

Сущность метода с точки зрения процессов теплопередачи заключается в нагреве листовой заготовки для Т>Тст и охлаждении изделия, полученного после формования. В машинах для пневмо-вакуум формования используют все три метода нагрева: лучистый, конвективный и кондуктивный. При лучистом нагреве тепловой поток определяется уравнением Стефана-Больцмана, при конвективном – уравнением Ньютона-Рихмана, при контактном (кондуктивном) – уравнением Фурье. Время прогрева листа до требуемой температуры (Т>Тст или Т>Ткрист) при лучистом нагреве можно рассчитать по формуле: tнагр = Sδсρ (Тф – Тнач)/qизл, (4.56)

где qизл =σизлεφ S(Т14-Т24), Sл, δл и Тнач – площадь, толщина и начальная температура листа, с и ρ –плотность и теплоемкость полимера, Тф – температура формования, σизл и ε – коэффициент излучения и степень «черноты» излучателя, φ – коэффициент использования потока, Т и Sизл – температура и площадь излучающей поверхности, Т2 средняя температура обогреваемой поверхности (Т2 = Тф + Тнач)/2. Максимальную температуру на обогреваемой поверхности листа при одностороннем его нагреве можно рассчитать по уравнениям нестационарной теплопроводности: (4.57)

Тмакс = Тнач+ (qизл δл/λ Sл)[Fo +1/3 – (2/π2) Σ (1/n2) exp( -π2 n2 Fo)]

Температуру на обратной стороне листа можно рассчитать из похожего уравнения:

Тмин=Тнач+(qизлδл/λSл)[Fo-1/6–(2/π2)Σ(-1/n2)exp(-π2n2Fo)]. (4.58)

Нагретую до необходимой температуры заготовку подвергают формованию, а затем охлаждают до температуры ниже Тст или Ткрист. Охлаждение изделия осуществляют за счет кондуктивного отвода тепла поверхностью формы (одностороннего или двухстороннего), за счет конвективной теплоотдачи при обдуве воздухом или комбинированным способом. Время охлаждения изделия при двухстороннем теплоотводе составляет: tохл =[2,3 δ2/ π2a] lg[(4/π)(Тф-Тохл)/(Ткон-Тохл), (4.59)

где Тф – температура заготовки в момент формования, Ткон – конечная температура, Тохл – температура охлаждающей среды. При одностороннем теплоотводе время tохл составляет: tохл =[2,3 δ2/ π2a] lg[(9,2/π)(Тф-Тохл)/(Ткон-Тохл)]. (4.60)

Лекция 5. КИНЕТИКА.

Третьей особенностью, сопровождающей переработку полимерных материалов, является то, что переработка реактопластов сопровождается различными химическими реакциями (механодеструкции, отверждения, сшивания, полимеризации, поликонденсации и т. п.). Закономерности изменения химической структуры смолы при этом описываются специальной областью науки - химической кинетикой. Известно, что кинетические закономерности процессов характеризуются такими понятиями как константа скорости, порядок реакции, энергия активации процесса отверждения и др. Сложность процессов полимеризации, например, состоит в том, что в этом процессе одновременно изменяется и молекулярная масса образующихся молекул, и их концентрация в системе. На скорость химических превращений оказывает влияние концентрация реагирующих веществ и температура процесса, наличие катализаторов, инициаторов или ингибиторов и даже вязкость окружающей среды. Поэтому кинетика является третьей составляющей, определяющей переработку. Кинетические закономерности следует принимать во внимание, даже если никаких химических процессов в материале не происходит, а происходит изменение его фазовой структуры (плавление или кристаллизация). Эти процессы также сопровождаются заметным выделением или поглощением тепла, способным менять условия переработки полимерных материалов, и идут во времени часто с различными скоростями, сопоставимыми с интервалом переработки. В ряде случаев ранее известные закономерности меняются в такой степени, что это привело к созданию новых областей науки. Например, это можно сказать про закономерности изменения вязкостных свойств, сопровождающих процессы химических превращений в полимерных материалах, которые заняли такое важное место в исследовании полимеров, что превратились в новую науку - реокинетику. Отверждение термореактивных смол представляет собой сложный процесс, который может включать несколько одновременно проходящих реакций (параллельных или последовательных), каждая из которых характеризуется собственным порядком реакции, константами скорости и их температурной зависимостью. Для анализа подобных сложных систем обычно применяют современные методы анализа, включающие химическое титрование и анализ УФ или ИК - спектров получаемых продуктов на разных стадиях отверждения. К сожалению, полностью или частично сшитые продукты реакций отверждения термореактивных смол, как правило, нерастворимы. Поэтому большинство аналитических методов к кинетическому анализу подобных продуктов неприменимо.

ФАЗОВО-РЕЛАКСАЦИОННАЯ ДИАГРАММА

Т а V 1

а

Tg¥

б II

III в

5

2

I

3

Tg0 б

в IV

4

время t

Рис.10. Фазово-релаксационная диаграмма Гиллхема

Наиболее общую информацию об особенностях процесса отверждения термореактивных материалов можно получить, рассматривая т. н. фазово-релаксационную диаграмму Гиллхема [6]., приведенную на рис.10, ординатой которой является температура, а абсциссой – время отверждения.

Линией а-а (штрих-пунктир) на рисунке 10 обозначена область, выше (и правее) которой происходит деструкция материала. Для этой области характерны высокие температуры и большие промежутки времени. Линией б-б (штрих-пунктир) обозначена область, выше (и правее) которой происходит сшивание (гелеобразование) материала. Время гелеобразования для термореактивных материалов, естественно, уменьшается с ростом температуры. Изогнутой линией в-в на рисунке ограничена область стеклования материала (стеклообразное состояние систем справа от линии в-в). Таким образом, на диаграмме можно выделить четыре области.

I – область, в которой несшитый материал находится в жидком (вязкотекучем) состоянии);

II – область, в которой сшитый материал находится в высокоэластическом состоянии;

III – область, в которой сшитый материал находится в стеклообразном состоянии;

IV – область несшитого стекла;

V – область деструкции.

При проведении процесса отверждения в соответствии с тонкими пунктирными линиями 1-4 (т. е. в изотермических условиях) отверждение в соответствии с линией 1 приведет к деструкции материала. Соответствие процесса линии 2 дает нормально отвержденный материал. Соответствие процесса линии 3 не дает гарантии отверждения материала, т. к. материал раньше перейдет в стеклообразное состояние, в котором реакции отверждения резко замедлятся. Соответствие процесса линии 4 также не дает отвержденного материала, т. к. уже с самого начала мы будем иметь дело с застеклованной смолой и можем вообще не достичь линии сшивания. Фазово-релаксационная диаграмма Гиллхема хорошо объясняет – почему процесс отверждения, проводящийся при постоянной температуре, ограничен весьма узкими рамками, т. к. нормальное прохождение процесса сшивания обеспечивается только режимом 2. По этой диаграмме легко проследить и за ходом процесса, проводящегося при переменной температуре (например, по ломаной пунктирной линии 5 на рис.10).

АНАЛИЗ КИНЕТИКИ ОТВЕРЖДАЮЩИХСЯ СМОЛ

Информацию об изменении свойств отверждающейся системы на начальных стадиях отверждения можно получить, измеряя её вязкость [6]. На более глубоких стадиях отверждения одним из немногих пригодных методов остаётся дифференциальный термический или калориметрический анализ, т. к. для измерения теплового эффекта реакции нет необходимости в растворении образующихся продуктов. В этом случае кинетическое уравнение, описывающее изменение скорости реакции отверждения с позиций закона действующих масс,имеет следующий вид (уравнение Вант-Гоффа): da/dt = K. (1-a)n (5.1) , где a - степень конверсии (отверждения) смолы, которую можно рассчитать, например, соотнося тепло, выделившееся за определённый промежуток времени - q(t) и полное тепло реакции – Q в виде: a = q(t)/Q; n - порядок реакции, а К - константа скорости, зависящая от температуры реакции по уравнению Аррениуса: K = K0.exp(E/RT), (5.2)

где К0 - предэкспоненциальный множитель, а Е - энергия активации процесса отверждения. В случае реакции первого порядка (n=1) решение дифференциального кинетического уравнения (5.1) представляет собой следующее выражение: a = 1 - ехр(-Kt), (5.3), где t - время. Величину константы скорости можно определить, если построить экспериментальную кривую в координатах: ln(1-a) – t. Тогда константа определяется по углу наклона кинетической кривой. Для реакции второго порядка (n=2) решение уравнения 5.1 представляет собой следующее выражение: a = 1 - 1/Kt. (5.4)

и константу скорости следует определять по наклону кинетической кривой в координатах: 1/(1-a) – t. Существенно усложняется процесс кинетического анализа в том случае, когда неизвестен заранее порядок реакции. Тогда применяют следующий подход. Кинетическую зависимость выражают более сложным вариантом уравнения 5.3: a = 1 - ехр(-Ktm), (5.5)

Это уравнение носит имя Ерофеева-Колмогорова и способно описать практически любую пологую зависимость. Как же его анализировать? Попробуем прологарифмировать:

ln(1-α) = - Ktm . Мало! Переносим знак минуса в левую часть и логарифмируем еще раз: ln[-ln(1-α)] = lnK + m ln t. . Теперь в координатах ln[-ln(1-α)] и ln t по углу наклона кинетической кривой можно определить величину показателя степени m. Если эта величина равна или близка к 1 (0,7-1,5), то исследуемую зависимость можно анализировать в координатах уравнения 1 порядка. Если нет – то необходимо более подробное изучение кинетики по стадиям, т. к. равенство величины m какому-либо числу (2 или 3) не говорит о втором или третьем порядке реакции.

АНАЛИЗ РЕОКИНЕТИКИ ОТВЕРЖДАЮЩИХСЯ СМОЛ

Еще более сложная картина наблюдается при оценке кинетических параметров реакции отверждения методами реологии. Известно [5], что изменение вязкости во времени для системы, отверждающейся по механизму радикальной полимеризации описывается уравнением:

h = h0 Ka+b I0,5 ta+b, (5.6)

где h0 - начальная вязкость системы, К - константа скорости реакции отверждения, I - концентрация инициатора, t - время. Показатели степени a и b зависят от механизма нарастания вязкости в системе. Начальная вязкость и константа скорости реакции зависят и от температуры:

h0 = A exp(E1/RT) и K = k exp(-U1/RT).

Энергия активации вязкого течения Е1 зависит от молекулярной массы текущего вещества и составляет для мономеров 5-20 КДж/моль, а для полимеров 50-100 КДж/моль. Энергия активации отверждения U1 зависит от типа процесса отверждения и составляет обычно 40-100 КДж/моль.

Для системы, отверждающейся путём полимеризации, нарастание наибольшей ньютоновской вязкости определяется одновременным увеличением молекулярной массы полимера и увеличением его концентрации (в мономере). Эти зависимости имеют характер, представленный ниже (рис.11), причём изменение наклона прямых в двойных логарифмических координатах происходит при достижении критической величины молекулярной массы (при образовании флуктуационной сетки зацеплений) и при достижении критической концентрации раствора полимера в собственном мономере (при перекрывании клубков макромолекул). Показатели степени в этих уравнениях определяют величины коэффициентов a и b, (причём n1 и m1 » 1, m2 = a и n2 = b), а их величина зависит от типа мономера, например для ПС a = 3,4; b = 5,5; для ПММА a =3,4; b = 12,8.

lgh m2 lgh n2

m1 n1

0 Мкр lgM 0 Cкр lgC

Рис.11. Схемы зависимости вязкости полимера от молекулярной массы и концентрации полимера в полимеризующейся системе.

Для системы, отверждающейся за счет прохождения процесса поликонденсации, существует только левая зависимость, т. к. при первом же шаге поликонденсации исчезает исходный мономер, при втором - димер и т. д.

Все это, в целом, выражается следующим уравнением:

h = h0 x0a Ka ta, (5.7)

где х0 – функциональность реагирующего вещества (две, три, четыре функциональные группы могут взаимодействовать с другими молекулами). Изменение молекулярной массы отверждающейся смолы и в этом случае приводит к изменению энергии активации вязкого течения, что усложняет анализ неизотермических процессов.

Если рассматривать реокинетические соотношения с точки зрения переработки пластмасс, то для нас важна скорость нарастания вязкости в отверждающейся системе. В координатах «логарифм вязкости – логарифм времени отверждения» она выражается ломаной прямой. Вначале скорость нарастания вязкости невелика (показатель а ≈1), а затем очень высока (показатель а>3). Поэтому с этой точки зрения целесообразно ограничить время безопасной переработки отверждающегося материала, которое должно быть меньше времени излома на реокинетической кривой в двойных логарифмических координатах.

АНАЛИЗ СЛОЖНЫХ КИНЕТИЧЕСКИХ ПРОЦЕССОВ

В конце лекции я хочу вернуться к уравнению Вант-Гоффа. Уравнение 4.1 справедливо только для относительно простых процессов первого или второго - третьего порядка. Однако если вспомнить общий вид константы скорости, которая, например, для процесса полимеризации, является отношением произведения констант скорости инициирования и роста цепи к константе обрыва: К = Кр. Кин1/2/Кобр1/2 (5.8)

При нарастании вязкости реакционной смеси константа скорости роста цепи меняется мало (она зависит от подвижности небольших молекул мономера), константа скорости инициирования меняется мало (она зависит от подвижности небольших молекул инициатора), а константа скорости обрыва цепей падает сильно (она зависит от подвижности макрорадикалов). Поэтому при определенной вязкости реакционной смеси наблюдается резкое возрастание скорости полимеризации (гель-эффект). Это можно отразить в изменении формулы 5.1: da/dt = K. (1-a)n(1+c.a) (5.9)

Для этого уравнения решения для реакций 1 и 2 порядка существуют, но выглядят сложнее:

при n=1 ln[(1+ca)/(1-a)] = (1+c)kt,

при n=2 a/(1-a) + c/(1+c)ln[(1+ca)/(1-a)]=(1+c)kt,

Существуют не только процессы, идущие с автоускорением, как вышеуказанный, но и процессы, идущие с автоторможением. Они наблюдаются в тех случаях, когда выделяющиеся продукты реакции (например, вода) ингибируют основную реакцию. Они также выражаются более сложным уравнением: da/dt = K. (1-a)n(1-ξ..a) (5.10)

где ξ – константа скорости автоторможения. В целом, возможно описание кинетики даже самой сложной одностадийной реакции с автоускорением и автоторможением:

da/dt = K. (1-a)n(1+c.a) (1- ξ..a) (5.11)

Для реакций 1 порядка оно выглядит следующим образом:

Ln[(1+ca)c(1- ξ)(1- ξa) ξ (1+c)/(1-a) ξ +c] = (1+c)(1- ξ)(ξ+c)kt (5.12)

Следует отметить, что при степени конверсии исходной смолы, большей 30%, эффективный порядок реакции отверждения, как правило, не превышает 1.

Лекция 6. МАКРОКИНЕТИКА.

АНАЛИЗ ТЕМПЕРАТУРНЫХ ПОЛЕЙ, РАЗВИВАЮЩИХСЯ

ПРИ ОТВЕРЖДЕНИИ ИЗДЕЛИЙ ИЗ ПКМ, НА БАЗЕ ЧИСЛЕННЫХ РЕШЕНИЙ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ.

Интенсивное выделение тепла в ходе многих кинетических процессов, оказывающее важнейшее влияние на скорость и ход этих процессов, особенно в случае больших объёмов реагирующих веществ, привело к созданию особой науки - макрокинетики, изучающей, среди прочих, процессы, происходящие при отверждении термореактивных полимерных материалов, сопровождающемся заметным разогревом. Расчет температурных полей при нагревании полимерных изделий, сопровождающимся изменением химического состава материала за счёт прохождения реакций сшивания, вулканизации, отверждения обычно описывается дифференциальным уравнением в частных производных с внутренним источником тепла: T/t=а(2T/x2+2Т/y2+2T/z2)+qвн/cr (6.1)

где qвн – интенсивность внутреннего источника тепла, а произведение сr соответствует теплоемкости единицы объема материала. Если процесс отверждения проводят в печах, т. е. при граничных условиях III рода, то интенсивность теплообмена реагирующей массы с окружающей средой, в общем случае, можно записать как: qнар = α.[Tизд (t) – Tокр(t)], где α – коэффициент теплоотдачи. Интенсивность внутреннего источника тепла меняется во времени в соответствии с протеканием химической реакции: qвн(t) = α(t).Q∞, здесь α – степень конверсии связующего, а Q∞ - полная теплота реакции отверждения, которая для термореактивных смол или мономеров может достигать 1000 Дж/г. Скорость отверждения связующего dα/dt определяется уравнением Вант-Гоффа:

dα/dt = К(1-α)n, где К = k0 exp(-U/RT).

Нахождение решения уравнения (6.1) или других уравнений в частных производных аналитическими методами для произвольных начальных, граничных и физических условий представляет собой очень сложную задачу и зачастую отсутствует. Для моделирования реальных процессов, которые описываются уравнениями подобного типа, кроме аналитических методов, разработаны численные методы решения. Можно выделить следующие основные методы: метод конечных разностей, различные варианты вариационных методов, метод Монте-Карло и т. д. Рассмотрим наиболее простую и достаточно наглядную разновидность метода конечных разностей (МКР) – метод Шмидта.

МЕТОД ШМИДТА

Производные в дифференциальном уравнении заменяют на конечные разности. Первым шагом в численном методе решения является разбиение пространства, занимаемого моделируемой системой, на отдельные ячейки.

Рассмотрим уравнение теплопроводности для бесконечной пластины: T/t = а (2T/x2). Температура в каждой точке зависит от двух переменных Т =f(x, t).

К элементов по ∆t

Tn, k+1

Tn-1,k Tn, k Tn+1,k Рис.12. Сетка разбиения

Tn, k-1 объема на элементы.

N элементов по ∆х

Составим сетку так, чтобы по горизонтали происходило изменение по х, а по вертикали – по t. Попробуем описать правую часть уравнения в конечных разностях: первая производная

∆T1/∆x1 = (Tn+1,k – Tn, k)/ ∆x1 ; ∆T2/∆x2 = (Tn+1,k – Tn-1,k)/ ∆x2

вторая производная

(∆T1/∆x1 - ∆T2/∆x2)/ ∆x = (Tn+1,k – 2Tn, k+ Tn-1,k)/ ∆x2.(5.2)

Опишем теперь левую часть уравнения:

∆T/∆t = (Tn, k+1 – Tn, k)/ ∆t. (6.3)

Одно из уравнений имеет в знаменателе ∆х, а другое - ∆t. Следует указать, что величины ∆х и ∆t мы выбирали произвольно, поэтому их можно связать равенством, принимая критерий Фурье равным 1/2: ½ = Fo = at/x2 = a∆t/∆x2. Отсюда ∆t = ∆х2/2а. Подставляем эти значения в уравнения 5.3 и то, что получилось - в уравнение теплопроводности:

а [ (Tn+1,k – 2Tn, k+ Tn-1,k)/ ∆x2 ]/ ∆х2 = 2a (Tn, k+1 – Tn, k)/ ∆x2, отсюда

Tn, k+1= (Tn+1,k + Tn-1,k)/2, таким образом положение точки Tn, k+1 можно рассчитать, зная положение трех точек Tn+1,k, Tn, k, Tn-1,k. Зная изменение Т по координате можно рассчитать его изменение по времени.

ОБОБЩЕННЫЙ ВАРИАНТ МКР

В общем случае по методу конечных разностей в центр каждой ячейки помещают узел и приписывают ему свойства всей ячейки (теплопроводность, теплоемкость, плотность и т. д.). Производные в дифференциальном уравнении заменяют на их аппроксимацию конечными разностями (или строят на основе законов сохранения конечно-разностный аналог дифференциального уравнения). Например, производная температуры T по времени t равна: dT/dt= limDt®0 DT/Dt, (6.3)

где DT = T2 - T1, т. е. разность температур, соответствующая шагу по времени Dt = (t2 - t1). Для расчета величины производной температуры по времени также можно взять не левую часть уравнения (5.1), а правую, при некотором малом, но конечном значении Dt. Система дифференциальных уравнений, таким образом, преобразуется в систему алгебраических уравнений, решением которой является численное приближение искомой функции. В этом случае конечно-разностное уравнение для внутреннего узла композиционного материала имеет вид [6]: Tit+Dt = FoD(Ti-1t + Ti+1t) + (1-2 FoD) Tit .

Для построения модели при наличии в твердом теле внутренних источников тепла, выделяющегося в процессе реакции отверждения композитов на основе термореактивных смол, при описании условий однозначности необходимо учесть, что изготавливаемое изделие можно представить в виде плоской пластины (или комбинации плоских элементов), тогда уравнение Фурье можно привести к одномерному варианту. Начальными условиями для исследуемого процесса можно принять: a = 0 (при t=0), T = T0 (при t=0). Граничные условия для решения уравнения можно определить как условия I рода и задать температуру формы Тф. Если задавать граничные условия III рода, что гораздо больше соответствует действительным условиям процесса отверждения, то для решения задачи необходимо задаться температурой окружающей среды – Токр и коэффициентом теплоотдачи.

Выше было показано, что кинетика выделения тепла при отверждении термореактивных смол (для реакции первого порядка) может быть описана уравнением Вант-Гоффа. В тепловом виде это уравнение можно переписать следующим образом: q = Q¥(1- exp(-Kt)), где q - количество выделившегося тепла за время t, Q¥ - полная теплота реакции отверждения, K - константа скорости реакции, зависящая от температуры. Таким образом, количество выделяющегося тепла есть функция, как степени завершенности реакции, так и температуры. Количество тепла, поступающее в узел, определяется дифференциальным уравнением: dq/dt = k (1-a) , где a - степень завершенности реакции. В нашем случае она может быть определена по величине q/Q¥. Конечное количество тепла, поступившее в объем за время D, получим, заменяя дифференциалы конечными разностями: Dqi = k (1-ai) (Dt ).

Поскольку расчет зачастую проводят для высоконаполненных композиционных материалов, то значение теплоты реакции для композита необходимо определять с учетом объемной доли связующего в нем:qj= q¥ (1-j),

где j - объемная доля наполнителя в композите.

РЕШЕНИЕ ЗАДАЧИ ТЕПЛОПРОВОДНОСТИ

В ГРАНИЧНЫХ УСЛОВИЯХ III РОДА.

Для построения модели нестационарной теплопроводности при наличии внутренних источников тепла можно воспользоваться вышеприведенными уравнениями. Если использовать величины теплоты реакции и теплоемкость материала, отнесенные к единицу массы материала, то их отношение позволяет определить изменение температуры, как на единицу массы, так и на единицу объема реакционной среды. В этом случае конечно-разностное уравнение для внутреннего узла композиционного материала имеет вид [6]: Tit+Dt = FoD(Ti-1t + Ti+1t) + (1-2 FoD) Tit + Dqi/с.

Решая уравнения совместно, получим значения температур на каждом шаге по времени. На рис.12 представлены зависимости температуры, развивающейся в центре и на поверхности пластины из композиционного материала, и соответствующей степени конверсии связующего от времени для изделий, отверждающихся при комнатных условиях (1) или в печи при температуре 1Эти зависимости показывают, что оба режима отверждения приводят к возникновению в изделии больших перепадов температур и степеней конверсии, т. е. к появлению значительных внутренних напряжений в изделиях. При отверждении, происходящем при комнатных условиях, внутренние части изделия, разогревающиеся до более высокой температуры, усаживаются больше, чем наружные, которые частично охлаждаются за счет окружающей среды. Отверждение и усадка наружных частей изделия приводят к его разрушению (трещины). Отверждение при повышенных температурах приводит, наоборот, к более быстрому отверждению наружных частей изделия. При завершении отверждения внутренних частей изделия также происходит его растрескивание.

РЕШЕНИЕ ЗАДАЧИ ТЕПЛОПРОВОДНОСТИ

В ГРАНИЧНЫХ УСЛОВИЯХ IV РОДА.

Для построения модели решим задачу тепловыделения в заданном объеме термореактивной смолы при отсутствии теплопередачи, т. е. адиабатическом режиме. Одним из вариантов получения подобного режима является поддержание температуры среды, окружающей отверждающийся образец композита, в точности равной температуре в центре образца.

Воспользовавшись приведенными выше уравнениями, составим схему расчета температуры в случае адиабатического протекания реакции отверждения термореактивной смолы: Tt+Dt = Tt + Dqi /с

Совместное решение уравнений позволяет получить зависимости температуры в центре и на поверхности изделия от времени и координаты. Она характеризуется полным отсутствием перепадов температуры реакции отверждения в течение всего процесса (кривая 3).

 

Т Токр=250 Т 1000 1 Т

2 3

2

 

1

t t t

Рис.13. Зависимость температуры на поверхности (1) и в центре (2) изделия из композиционного материала на основе эпоксидной смолы при комнатных условиях отверждения, при температуре 1000 и в адиабатическом режиме (3).

РАЗРАБОТКА НОВЫХ МЕТОДОВ ПЕРЕРАБОТКИ

ПОЛИМЕРОВ НА ОСНОВЕ МАТЕМАТИЧЕСКОГО

МОДЕЛИРОВАНИЯ.

Примером нового метода, разработанного на базе математического моделирования, является т. н. RIM – процессы (reaction injection molding), т. е. процесс получения методом экструзии листов из ПММА, заключающийся в том, что в экструдер заливается ММА и перекисный инициатор. В экструдере происходит полимеризация. За счет экзотермического эффекта происходит разогрев массы и ускоряется процесс. В момент подхода к головке экструдера полимеризация мономера завершена, и получающийся лист состоит из готового полимера. Естественно этот процесс требует во много раз меньше энергии, т. к. отсутствуют промежуточные нагревы и охлаждения, не теряется тепло полимеризации и т. п. Конечно, для осуществления такого процесса необходимо точнейшее поддержание предварительно рассчитанного режима. Другим примером является процесс литья под давлением композиций на основе пластифицированного ПВХ, отличающийся тем, что в литьевую машину загружают не готовую композиций, а дисперсию ПВХ в пластификаторе – пластизоль.
В целом, применение метода моделирования позволяет технологу – переработчику зряче контролировать процессы, происходящие внутри сложных машин и установок при высоких температурах и давлениях.

ЗАКЛЮЧЕНИЕ.

Моделирование базовых процессов, протекающих при переработке пластмасс, представленное в этой главе в виде отдельных тем (теплопередача, реология, кинетика), направлено прежде всего на формирование ясного представления о характера этих процессов. Приведенные в этой главе упрощенные модели теплопередачи, течения вязких полимерных жидкостей, химических процессов отверждения реактопластов позволяют установить основные характеристики процессов переработки и, что не менее важно, оценить их производительность.

Для более детального анализа процесса охлаждения перерабатываемого расплава пластмассы, например, с целью определения величины и направления усадки, необходимо использование усложненной модели полимерного вещества, в том числе, учитывающей процессы кристаллизации, ориентации в поле механических напряжений и соответствующие термомеханические характеристики. В этом случае может быть оценена неравномерность температурного поля, возникающего при охлаждении, и возможность коробления пластмассового изделия.

Для решения подобных задач применяются такие широко известные программные продукты как Mold Flow, C-Mold, подобные расчеты включения в конструкторские комплексы Solid Works и Pro Engineer. Их применение требует грамотного использования моделей полимерных материалов, адекватных методам и целям расчета.

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

1. Закгейм в моделирование химико-технологических процессов. М.: Химия, 1982, с.168.

2. В., «Теплотехника», М.: Высшая школа. 1986, с.322.

3. Мак- «Переработка полимеров», М.: Химия, 1965, с.442.

Теоретические основы переработки полимеров. М.: Химия, 1985. с. 628.

4. , , «Расчёт и конструирование оборудования для производства и переработки полимерных материалов». М.: Химия, 1986, с.567.

5. , «Реология в процессах образования и превращения полимеров», М.: Химия, 1985, с.367.

6. , Суриков процессов переработки пластмасс. Учебно-методическое пособие. М, МИТХТ, 2001, с.86.

7. , Симонов-Емельянов аналитических и проблемных задач по курсу «Принципы создания полимерных композиционных материалов». Учебно-методическое пособие. М, МИТХТ, 1999, с.93.

Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4