Моделирование процессов переработки пластмасс (стр. 2 )

Физические условия в данном случае требуют знания величины температуропроводности материала – а. К начальным условиям относятся температура тела в начальный момент процесса (при t=0). Обычно в этих случаях задают значение начальной температуры изделия или расплава. Граничные условия учитывают условия теплообмена на границе тела с окружающей средой. Они могут быть заданы четырьмя различными способами: при граничных условиях I рода задаётся распределение температур на границе тела (например, температура формы при литье); при граничных условиях II рода задаётся плотность теплового потока на поверхности тела (например, тепловой поток от нагревателей в процессе лучистого нагрева при вакуум-формовании); при граничных условиях III рода задаётся температура окружающей среды и интенсивность теплообмена на поверхности - т. н. коэффициент теплоотдачи - a [Вт/м2.0К] или его приведённое значение, выражающееся в виде критерия Био: Bi = al/l, где l - характеристический размер тела (например, при охлаждении изделий после экструзии); при граничных условиях IV рода переход тепла через границу отсутствует (например, при адиабатических процессах отверждения композитов на основе термореактивных смол, идущих без теплоотвода). Рассмотрим варианты решения уравнения теплопроводности [2].

Стационарная задача: Для плоской стенки с толщиной - D и температурой на поверхностях Т1 и Т2 при отсутствии внутренних источников тепла уравнение (2.1) имеет вид: d2T/dx2 = 0 (2.1б)

Его решение при граничных условиях I рода:

T(x) = T1 - (T1-T2).x/D (2.2),

т. е. температура меняется с изменением расстояния от стенки - x по линейному закону.

Стационарная задача в присутствии внутреннего источника тепла: В плоской пластине с толщиной - Δ и температурой на стенках Т1 присутствует внутренний источник тепла мощностью qвн. В этом случае уравнение (2.1) имеет вид:

d2T/dx2 + qвн/сρ = 0 (2.1в)

Его решение при граничных условиях I рода имеет вид:

Т(х) = Т1 + (qвн /2λ)[(Δ/x/2)2] (2.3),

т. е. температура в пластине меняется по толщине по кривой второго порядка (параболе).

Нестационарная задача: Для одномерного температурного поля при отсутствии внутренних источников тепла процесс описывается уравнением (2.1а). Это более сложный вариант, т. к. необходимо решать уравнение в частных производных от двух переменных - x и t. Для неограниченной плоской стенки с толщиной - D при температуре на поверхности (при x=D), равной Токр, и начальной температуре (t=0), равной Т0 , решение уравнения (2.1а) можно получить в виде произведения двух функций, каждая из которых зависит только от времени - j(t) или от координаты - y(x). Решение этого уравнения подробно описано в литературе [2]:

ln[j(t)] = - a. k2.t + lnC1 (2.4)

и y(x) = C2.cos(kx) + C3.sin(kх) (2.4а).

Определив значения постоянных интегрирования С1, С2, С3 и константы k2 и подставив полученные решения в уравнение (2.1а) распределение температур при заданных граничных условиях 1 рода после преобразований имеет вид: (2.5)

T(x,t) = Tокр + (T0-Tокр).å n (-1)n+1(2/mn) cos(mn.x/D)exp(-mn2.Fo)

где mn=(2n-1).p/2, Fo - критерий Фурье (Fo = a.t/D2), имеющий смысл приведённого времени, n - число членов уравнения (2.5), принимаемое при решении (чем их больше, тем точнее решение). Анализ показывает, что температура в центре и у поверхности изменяется во времени по сложной экспоненциальной кривой. В начальный момент времени она равна Т0, а при контакте с нагревателем возрастает. Изменение температуры от поверхности к центру также описывается сложной тригонометрической кривой.

Подобным образом решаются задачи теплопроводности и при наличии внутренних источников тепла – qвн. Так например, для тех же условий при наличии постоянного источника тепла решение уравнения Фурье

имеет вид ¶T/¶ t = а(¶2T/¶x2) + qвн/сρ (2.1г)

Его решение имеет вид: (2.6)

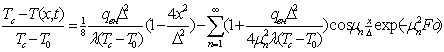
и выражается еще более сложной тригонометрической кривой.

В целом, применение уравнений теплопроводности к анализу процессов переработки пластмасс позволяет количественно рассчитать изменение температурных полей в перерабатываемом материале в течение всего процесса переработки.

Анализ температурных полей при охлаждении изделий, полученных методом литья под давлением в форму с постоянной температурой (т. е. при граничных условиях I рода) и изделий, полученных методом экструзии с охлаждением на воздухе или в воде (т. е. при граничных условиях III рода), можно проводить, используя описанное выше аналитическое решение уравнения Фурье или метод конечных разностей (см. лекцию 5).

КОНВЕКТИВНЫЕ ПРОЦЕССЫ

Конвективный теплообмен – это процесс переноса теплоты самим теплоносителем. Как правило, он происходит с участием текучей среды (жидкость, газ) и обычно сопровождается теплопроводностью. Плотность конвективного теплового потока – qконв пропорциональна тепловому напору, т. е. разности температур между температурой жидкости (газа) и температурой омываемой стенки, и определяется уравнением Ньютона-Рихмана: qконв ~ α (Тж – Тс), (2.7)

где α – коэффициент теплоотдачи. При переработке полимерных материалов вклад конвекции в передачу тепла от нагревающих или охлаждающих элементов оборудования к полимеру незначителен из-за высокой вязкости расплава полимера. Однако этот вклад становится определяющим при охлаждении расплава после экструзии в ванне с водой (для труб или листов) или на воздухе (для пленки), а также при принудительном охлаждении литьевых форм водой. Значения коэффициентов теплоотдачи для систем металл – воздух обычно составляют: 5 – 30 Вт/м2 0К при т. н. свободной конвекции (естественном охлаждении поверхности) и 10 – 500 Вт/м2 0К при вынужденной (принудительной) системе охлаждения. Для системы металл – вода коэффициенты теплоотдачи при свободной конвекции лежат в пределах 100 – 1000 Вт/м2 0К, а при вынужденной конвекции составляют 500 – 10000 Вт/м2 0К. На практике, если нужно описать теплопередачу в твердом теле, пользуются числом Био: Bi = αl/λтв , где l – характеристический размер (толщина стенки слоя полимера, слоя металла формы), а λтв – теплопроводность твердого тела. Для описания теплопередачи при конвективном теплообмене с участием жидкости или газа применяют критерий Нуссельта: Nu = αl/λж,где λж – теплопроводность жидкости или газа.

Все вышеперечисленные решения уравнения теплопроводности для стационарных и нестационарных случаев получены при граничных условиях 1 рода (при постоянной температуре стенки), что обеспечивается омыванием ее потоком жидкости или газа при бесконечно большом коэффициенте теплоотдачи (Bi → ∞). Если же это условие не выполняется, то решения уравнений зависят от условий теплопередачи (α или Bi). Так например, решение задачи для одномерного температурного поля при стационарной теплопроводности с внутренним источником тепла и граничных условиях III рода определяется уравнением:

T(x) - Tж = (1/m)(qвн R2/λ)(1- x2/R2 + 2/Bi) (2.8)

где Т(x) – температура в точке с координатой x, Тж – температура омывающей жидкости, qвн – интенсивность внутреннего источника тепла, R – полутолщина омываемого тела, m – коэффициент, равный 2 для пластины, 4 – для цилиндра, 6 – для шара. Видно, что параболический закон распределения температур по сечению омываемого тела сохраняется.

При нестационарной теплопроводности решение уравнения Фурье для неограниченной пластины при граничных условиях III – рода вместо выражения 2.5 дает:

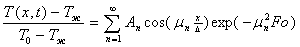(2.9)

где Аn = 2 sin μn/(μn + sin μn cos μn) . При заданных значениях x безразмерная температура Θ = [T(x, t) – Tж]/(T0 – Tж) зависит только от величины критериев Био и Фурье. Необходимо отметить, что для тел другой формы (шар, цилиндр) коэффициент Аn имеет иное значение.

ЛУЧИСТЫЙ ТЕПЛООБМЕН.

При переработке полимеров лучистый нагрев применяется для нагревания относительно тонких листов термопластов, подвергающихся затем вакуум - или пневмо-формованию. Это вид теплопередачи, не требующий непосредственного контакта более и менее нагретого тела, характеризуется передачей энергии в виде электромагнитных волн. Зависимость между температурой абсолютно черного тела Т1 и удельной излучаемой энергией Еизл на единицу поверхности описывается уравнением Стефана-Больцмана: Еизл = σизлТ,

где σизл – коэффициент Стефана-Больцмана, равный 5,67.10-8 Вт/м2 0К4. При рассмотрении излучения реальных «серых» тел в это уравнение следует внести коэффициент ε – степень черноты излучающей поверхности, составляющий обычно 0,8 – 0,9. Учитывая, что нагреваемый материал также способен излучать энергию, уравнение 2.3. можно переписать в следующем виде: Еизл = σ изл ε ψ (Т1 4 – Т24), (2.10а)

где Т2 – температура нагреваемой поверхности, ψ = cos γ – косинус угла между нормалью к поверхности и направлением излучения.

Лекция 3.

РЕОЛОГИЯ В ПРОЦЕССАХ ПЕРЕРАБОТКИ

ПЛАСТМАСС

Нагрев полимерного материала переводит его в податливое состояние, в котором можно придать ему нужную форму. Это является следующей задачей переработки полимеров, которую решают в соответствии с закономерностями их течения. «Течь» по-гречески произносится «reo» (рео), поэтому наука о течении получила название реологии. Закономерности течения расплавов и растворов полимеров отличаются от аналогичных закономерностей для большинства обычных жидкостей тем, что при течении большинства полимеров наблюдается т. н. «аномалия» вязкости, т. е. её изменение при изменении условий деформирования (скорости и усилия). Зачастую диапазон изменения вязкости при течении полимеров достигает 4-5 десятичных порядков, т. е. вязкость меняется в десятки и сотни тысяч раз. Конечно, это не может не влиять на процесс переработки, который существенно осложняется ещё и изменением температуры полимерного материала при литье, экструзии и т. п. Поэтому второй основной составляющей моделирования переработки пластмасс является именно реология.

УРАВНЕНИЯ СОСТОЯНИЯ

Реологические свойства полимерных жидкостей - расплавов или растворов полимеров, принципиально отличаются от свойств простых жидкостей, например - воды. Отличие реологии полимеров от гидравлики, изучающей течение воды, заключается ещё и в том, что по вязкости полимерные жидкости превосходят воду в 1раз. В ряде случаев для описания их течения неприменимы известные соотношения гидравлики и поэтому, проводить подобное описание следует с использованием фундаментальных уравнений физики: уравнения неразрывности, уравнения движения и уравнения энергии, формулирующихся следующим образом [3]:

1) Уравнение неразрывности или закон постоянства массы: ¶r/¶t = - [¶/¶x(rVx) + ¶/¶y(rVy) + ¶/¶z(rVz) (3.1)

Изменение массы (или плотности r=m/V) во времени определяется изменением массы (или плотности) по координатам. Возникновение массы в замкнутой системе невозможно - что приносится по одной координате, то уносится по двум другим.

Следствием этого уравнения для несжимаемых жидкостей, у которых ¶r/¶t = 0, является постоянство расхода при любом сечении канала Q = S . V = const. Поэтому для текущей жидкости всегда можно определить скорость течения V, зная сечение канала S.

2) Уравнение движения или закон сохранения количества движения в замкнутой системе (с учётом векторного характера скорости по трём координатам): (3.2)

r[¶Vx/¶t+Vx¶Vx/¶x+Vy¶Vx/¶y+Vz¶Vx/¶z]= -¶P/¶x+(¶txx/¶x+¶txy/¶y+¶txz/¶z)+rgx

r[¶Vy/¶t+Vx¶Vy/¶x+Vy¶Vy/¶y+Vz¶Vy/¶z]= -¶P/¶y+(¶tyx/¶x+¶tyy/¶y+¶tyz/¶z)+rgy

r[¶Vz/¶t +Vx¶Vz/¶x+Vy¶Vz/¶y+Vz¶Vz/¶z]= -¶P/¶z+(¶tzx/¶x+¶tzy/¶y+¶tzz/¶z)+rgz.

Изменение количества движения определяется изменением давления, внутренним трением и работой в поле сил тяжести – это система уравнений Коши. Для ньютоновских жидкостей напряжение сдвига можно выразить через скорость деформации в виде зависимости:txx=mdVx/dx, тогда система (3.2) превратится в т. н. систему уравнений Навье-Стокса (3.2а):

r[¶Vx/¶t+Vx¶Vx/¶x+Vy¶Vx/¶y+Vz¶Vx/¶z]= -¶P/¶x+m(¶2Vx/¶x2+¶2Vx/¶y2+¶2Vx/¶z2)+rgx

r[¶Vy/¶t+Vx¶Vy/¶x+Vy¶Vy/¶y+Vz¶Vy/¶z]= -¶P/¶y+m(¶2Vy/¶x2+¶2Vy/¶y2+¶2Vy/¶z2 )+rgy

r[¶Vz/¶t+Vx¶Vz/¶x+Vy¶Vz/¶y+Vz¶Vz/¶z]=-¶P/¶z+m(¶2Vz/¶x2+¶2Vz/¶y2+¶2Vz/¶z2)+rgz.

3) Уравнение энергии или закон сохранения энергии:

rCv(¶T/¶t+Vx¶T/¶x+Vy¶T/¶y+Vz¶T/¶z) = -[¶qx/¶x+¶qy/¶y+¶qz/¶z] –

T(¶P/¶t)r(¶Vx/¶x+¶Vy/¶y+¶Vz/¶z)+ (txx ¶Vx/¶x+tyy¶Vy/¶y+tzz¶Vz/¶z)+

{txy(¶Vx/¶y+¶Vy/¶x)+txz(¶Vx/¶z+¶Vz/¶x)+tyz(¶Vy/¶z+¶Vz/¶y)}. (3.3)

Изменение внутренней энергии с замкнутой системе определяется ее изменением за счет тепловых потоков, за счет сжатия единицы объема и за счет диссипации энергии при течении, обусловленном проявлением нормальных и касательных напряжений. Если учесть, что a = l/Cr, для несжимаемой жидкости ¶r/¶t = 0, и Cv = Cp, для ньютоновской жидкости t = mg’; тогда получим упрощенное уравнение:

rCv(¶T/¶t+Vx¶T/¶x+Vy¶T/¶y+Vz¶T/¶z) = a (¶2T/¶x2 + ¶2T/¶y2 + ¶2T/¶z2)

+2m[(¶Vx/¶x)2+(¶Vy/¶y)2+(¶Vz/¶z)2]+

m [(¶Vx/¶y+¶Vy/¶x)2+(¶Vx/¶z+¶Vz/¶x)2+(¶Vy/¶z+¶Vz/¶y)2] (3.3а)

т. е. перенос энергии связан со скоростями движения жидкости и тепловыми потоками в ней. Для неподвижной жидкости все переменные, включающие V, равны нулю и уравнение (3.3а) превращается в уравнение Фурье.

МОДЕЛИ ДЛЯ ОПИСАНИЯ ТЕЧЕНИЯ

ПОЛИМЕРНЫХ ЖИДКОСТЕЙ.

Прямые расчёты, связанные с уравнениями движения и энергии, очень трудоёмки. Поэтому в них вводят упрощения, например, об изотермичности течения (что упрощает уравнение энергии), или о несжимаемости жидкости (что верно только для невысоких давлений, но несправедливо, например, для описания процесса литья под давлением), или о ньютоновском характере течения. К сожалению, для полимерных жидкостей последнее предположение также не работает, т. к. их течение сопровождается т. н. аномалией вязкости. При сдвиговом течении низкомолекулярных жидкостей, как правило, выполняется закон Ньютона: t = m.g’ (3.4)

где t - напряжение сдвига, m - вязкость жидкости, g’ - градиент скорости сдвига. Вязкость при этом постоянна и её величина не зависит от условий деформирования жидкости. Для полимерных жидкостей уравнение Ньютона видоизменяется следующим образом: t = h.g’, (3.4а), где h - т. н. эффективная вязкость, значение которой меняется в зависимости от условий деформирования. Для описания зависимостей эффективной вязкости от условий деформирования существует ряд моделей, наиболее простой из которых является т. н. степенной закон: t = К.g’ n , (3.5), где n - показатель степени, учитывающий изменение вязкости (n<1). При таком описании сама величина вязкости зависит от скорости сдвига следующим образом: h = K.g’ n-1, (3.5а)

где К - коэффициент консистентности, а n - индекс псевдопластичности жидкости или индекс течения.

Более сложными являются трёхпараметрические уравнения, среди которых наиболее известны модели Карро и Эллиса [3]. В них устанавливается более сложная зависимость вязкости от условий деформирования. По модели Карро: h = h0.(1+(l.g’)2) (n-1)/2 (3.6), где h0 - т. н. наибольшая ньютоновская вязкость полимера, n - индекс течения (который может несколько отличаться от индекса течения из уравнений (3.5-3.5а)), а l - соотношение скорости релаксации и скорости деформации материала. По модели Эллиса:h=h0/(1+(t/tt)a-1(3.7),

где a - показатель степени, а tt - напряжение сдвига, при котором значение ньютоновской вязкости полимера падает в 2 раза.

lgh lgh lgh

1 2 3

lgg, lgg, lgt

Рис 1. Зависимость вязкости расплавов полимеров от интенсивности деформирования для степенной жидкости (1), жидкостей

Изменение вязкости при изменении скорости или напряжения сдвига в двойных логарифмических координатах выражается прямой линией (для степенного закона) или кривыми (для моделей Карро и Эллиса) – рис.1.Карро (2) и Эллиса (3).

ВИДЫ ТЕЧЕНИЯ, РЕАЛИЗУЮЩИЕСЯ ПРИ ПЕРЕРАБОТКЕ.

ПЛОСКО-ПАРАЛЛЕЛЬНОЕ ТЕЧЕНИЕ

Какие же виды течения реализуются в промышленных процессах переработки? Для выяснения характера распределения скоростей течения, градиентов скоростей сдвига и напряжений сдвига при плоско-параллельном течении (т. е. при течении жидкости между двумя плоскостями, одна из которых движется) проинтегрируем уравнения Коши и Навье-Стокса. Введем в них необходимые упрощения:

а) течение между двумя параллельными плоскостями представим как одномерное (в уравнениях 3.2 исчезают две координаты - x и y из трёх и два уравнения из трёх),

б) предположим, что течение является установившимся (изменение количества движения, а, следовательно, и левая часть уравнений 3.3 равна 0),

в) предположим, что течение происходит при атмосферном давлении (первый член правой части уравнений 3.2 равен 0),

г) предположим, что течение проходит в направлении, перпендикулярном ускорению свободного падения (последний член правой части уравнений 3.2 равен 0).

В результате упрощений уравнение 3.2 сводится к следующему: dtxz/dx = 0. Решением этого уравнения является: txz = const. , т. е. напряжение сдвига в зазоре при течении постоянно. Уравнение 3.2а сводится к уравнению: m.¶2Vx/¶x2 = 0, решением которого при граничных условиях прилипания жидкости к стенкам [vx(0)=0, vx(H)=Vx] и ненулевом значении вязкости, является dVx/dx = const , т. е. градиент скорости сдвига в зазоре при плоскопараллельном течении постоянен и равен Vx/H. Второе интегрирование этого уравнения даёт линейную функцию изменения Vx по зазору (рис.2).

y z z z z

x x x x

Скорость течения Скорость сдвига Напряжение сдвига

Рис.2. Эпюры распределения скоростей течения, скоростей и напряжений сдвига при плоскопараллельном течении жидкости.

ПУАЗЕЙЛЕВСКОЕ ТЕЧЕНИЕ

Для выяснения характера распределения скоростей течения, градиентов скоростей сдвига и напряжений сдвига при пуазейлевском течении (течение в цилиндрическом канале под действием перепада давлений) также необходимо интегрировать уравнения Коши и Навье-Стокса. Введем и в них те же упрощения:

а) при расположении оси координат в центре канала задача представляет собой частный случай одномерного течения,

б) при предположении об установившемся характере течения левую часть уравнений 3.2 также можно приравнять к нулю,

в) если течение осуществлять в направлении, перпендикулярном направлению силы тяжести, то последний член правой части уравнений 3.2 также должен быть равен нулю,

г) предположим, что перепад давления при течении постоянен и равен DP.

В результате упрощений уравнение 3.2 приобретает вид: dtxz/dx = const и его интегрирование даёт линейность распределения напряжения сдвига по радиусу цилиндрического канала. Уравнение 3.2а приобретает вид:

m d2Vx/dx2 = const и его интегрирование приводит (только для ньютоновской жидкости, для которой вязкость постоянна) к линейному характеру изменения градиента скорости сдвига по радиусу цилиндрического канала. Второе интегрирование этого уравнения указывает, что изменение скорости течения жидкости по радиусу цилиндрического канала соответствует квадратичной параболе (рис.3).

Для псевдопластичных жидкостей, характер течения которых описывается степенной моделью, величина вязкости зависит от скорости сдвига и общая формула градиента скорости сдвига имеет вид: d2Vz/dx2=(t/K)1/n и зависимость скорости сдвига от x становится степенной (с показателем степени, равным 1/n). Второе интегрирование, повышает показатель степени функции на единицу. Нелинейные зависимости скорости течения и скорости сдвига для псевдопластичных жидкостей показаны на рис.3 пунктиром.

Формулы для расчета: ньютоновское псевдопластичное

Напряжение сдвига τw = RΔP/2L τw = RΔP/2L

Скорость течения v0 = - R2ΔP/4μL v0 = -(n/n-1)γ0R(RΔP/2η0 L)1/n

Скорость сдвига γ” = -(2v0/R)(r/R) γ” = -(2v0/R)(n+1)/n (r/R)1/n

Скорость сдвига на стенке γ”w =-4Q/πR3 γ”w = - (3n+1)/n(Q/πR3)

v0 – скорость в центре канала (максимальная), γ0 – скорость сдвига при μ= η0 (для ньютоновской вязкости).

y z z z z

y - x 0 x - x 0 x - x 0 x

Скорость течения Скорость сдвига Напряжение сдвига

Рис.3. Эпюры распределения скоростей течения, скоростей и напряжений сдвига при пуазейлевском течении жидкости.

КУЭТТОВСКОЕ И ДРУГИЕ ВИДЫ ТЕЧЕНИЯ

Куэттовское течение осуществляется в зазоре между двумя коаксиальными цилиндрами, один из которых вращается (пример – пластометр Канвца). Интегрирование уравнений 3.2 и 3.2.а в этом случае требует больших усилий, но результирующие формулы получены и в этом случае (вращается наружный цилиндр):

Формулы для расчета: ньютоновское псевдопластичное

Напряжение сдвига τ = М/2πR2внутрL τ = М/2πR2внутрL

Скорость течения

v(r) = r.ω[(β2 – (Rнар.к)2]/(β2-1) v(r) = r.ω[(β2/n – (Rнар.к)2/n]/(β2/n-1)

Скорость сдвига

у внутреннего цилиндра γ” = 2ω/(1- β2) γ” = (1/n)2ω/(1- β2/n)

М – момент, необходимый для удержания неподвижным внутреннего цилиндра, β – соотношение радиусов напружного и внутреннего цилиндров.

Существуют также два особых вида течения в системе диск-диск и в системе конус - плоскость. Для них напряжение сдвига рассчитывается по формуле τ = 3М/πR3.

Скорость сдвига для системы конус-плоскость

γ” = ω/ψ (ψ – угол при вершине конуса, равный 1 -50), для системы диск-диск γ” = ωr/h, где r – текущий радиус диска, h – расстояние между дисками.

НОРМАЛЬНЫЕ НАПРЯЖЕНИЯ. ИХ ПРИЧИНЫ И РАСЧЕТ

Реализация различных типов течения полимерных жидкостей позволила обнаружить некоторые их интересные особенности, одной из которых является эффект Вейссенберга. Если в стакан с полимерной жидкостью (раствор полимера) опустить палочку и начать вращать ее, то жидкость начнет подниматься по палочке вверх. Если то же проделать с трубкой, то жидкость начнет подниматься по трубке. Подобные свойства для жидкостей ранее не наблюдались. Таким же необычным оказался эффект разбухания струи расплава полимера, вытекающей из трубки (капилляра) – Барус-эффект. Впоследствии обнаружили и другие эффекты – отталкивание дисков, вращающихся в полимерной жидкости. Если в одном из дисков есть отверстие и тормозить их отталкивание, то жидкость начнет выдавливаться из отверстия. На этом эффекте основано действие дискового экструдера. В чем же причина проявления этих эффектов? Она в возникновении т. н. нормальных напряжений (от слова нормаль). Что же это такое? В общем виде напряжения, возникающие при течении жидкости можно выразить т. н. тензором напряжений:

компоненты σxy = σyx ; σxz = σzx ;σyz = σzy называются касательными напряжениями. Они действую в плоскостях xy, xz, yz. Диагональные компоненты σxx ;σyy ; σzz - называются нормальными. Они действуют вдоль осей x, y, z. Для жидкостей, обладающих ньютоновскими свойствами, диагональные компоненты равны нулю, а для вязкоупругих жидкостей они нулю не равны: σxx – положительна, а σyy – отрицательна. Существует также графическая интерпретация проявления этих напряжений. Продеформируем квадрат АБВГ за счет действия сдвигового касательного напряжения τxy.