Моделирование микроэкономических процессов
лекции
Тема 1. Методы анализа и прогнозирования рыночной конъюнктуры
§1. Прогнозирование на микроуровне
Объектами прогнозирования на микроуровне (уровне предприятия, организации (фирмы)) – являются: спрос, производство продукции (выполнение услуг), объем продаж, потребность в материальных и трудовых ресурсах, издержки производства и реализации продукции, цены, доходы предприятия, его техническое развитие.
Субъектами прогнозирования являются планово-финансовые органы предприятия, маркетинговые и технические отделы.
Разработка планов-прогнозов (на перспективу, краткосрочные (год, квартал, месяц) и оперативные (сутки, декада)) происходит как в целом по предприятию, так и по его структурным подразделениям: цехам, участкам, службам.
Для принятия решения необходимо иметь достоверную и достаточно полную информацию, на основе которой формируется стратегия производства и сбыта продукции. В связи с этим повышается роль прогнозов, требуется расширение системы и совершенствование методов прогнозирования, применяемых на практике.
При прогнозировании показателей целесообразно использовать следующую систему методов: экспертные оценки, факторные модели, методы оптимизации, нормативный метод.
Особое внимание должно уделяться прогнозированию спроса на продукцию (услуги), издержек производства, цен и прибыли. Для чего проводятся исследования внутреннего и мирового рынков, осуществляется анализ эластичности спроса.
При разработке рекомендации по определению стратегии предприятия, оценки его финансового положения, определения потребности в инвестициях, привлечения финансовых средств и потенциальных партнеров рекомендуется применять пакеты прикладных программ. Наибольшее распространение в мировой практике получила методология по технико-экономическим исследованиям и обоснованию инвестиционных проектов, разработанная специалистами Организации по промышленному развитию при ООН. Также широко применяются программные продукты COMFAR, PROJEKT EXPERT и др., которые позволяют выполнить полный расчет эффективности проекта. Методология этих программ базируется на принципах расчета движения денежной наличности.
§2. Методы моделирования и прогнозирования
При прогнозировании экономики для решения обширного круга различных социально-экономических и научно-технических проблем, необходимо использовать методы, базирующиеся на математической теории: методы экстраполяции и методы моделирования.
Одним из методов экстраполяции является метод подбора функций, основанный на методе наименьших квадратов (МНК). В современных условиях большое значение стали придавать модификациям МНК: методу экспоненциального сглаживания с регулируемым трендом и методу адаптивного сглаживания.
Методы моделирования, используемые в процессе прогнозирования и планирования различного рода экономико-математические модели, представляют собой формализованное описание исследуемого экономического процесса (объекта) в виде математических зависимостей и отношений. Они предполагают конструирование модели, основанное на предварительном изучении объекта или процесса, выделения его существенных характеристик или признаков.
Различают следующие экономико-математические модели: матричные, оптимального планирования, экономико-статистические (трендовые, факторные, эконометрические), имитационные, принятия решений, для реализации которых применяются экономико-математические методы.
Прогнозирование экономических и социальных процессов, с использованием моделей, включает разработку модели, ее экспериментальный анализ, сопоставление результатов прогнозных расчетов на основе модели с фактическими данными состояния объекта или процесса, корректировку и уточнение модели.
Экономико-математическая модель состоит из целевой функции и системы ограничений.
Целевая функция описывает цель оптимизации, коэффициенты которой выражают влияние переменных на её величину.
Система ограничений отражает объективные экономические связи и зависимости и представляет собой систему равенств и неравенств. На микроуровне в качестве критерия оптимальности могут быть использованы экстремумы показателей: максимум прибыли, минимум затрат, максимум выпуска продукции (услуг) и др.
Модели по расчету оптимального варианта производства продукции имеют следующий общий вид:
Целевая функция
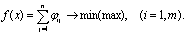
Система ограничений
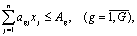
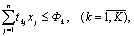
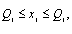
где jij – значение i-го показателя на единицу j-го вида продукции; agj – норма расхода, g-го вида сырья на производство единицы j-го вида продукции; xj – искомое количество j-го вида продукции; Ag – имеющийся фонд g-го вида сырья; tkj – затраты времени на k-м виде оборудования для производства единицы j-го вида продукции; Фk – действительный фонд времени работы k-гo вида оборудования; ![]() – нижний и верхний пределы выпуска j-гo вида продукции. Нижний предел устанавливается с учетом заданий на поставку продукции для государственных нужд, верхний – с учетом спроса на продукцию.
– нижний и верхний пределы выпуска j-гo вида продукции. Нижний предел устанавливается с учетом заданий на поставку продукции для государственных нужд, верхний – с учетом спроса на продукцию.
Эконометрической моделью называется система регрессионных уравнений и тождеств, описывающих взаимосвязи и зависимости основных показателей развития экономики. Они позволяют прогнозировать широкий круг показателей (ВНП, доходы населения, потребление товаров и услуг и др.).
Модели принятия решений основываются на теории игр и применяются в условиях неопределенности или в ситуациях, когда интересы сторон не совпадают. Каждая из сторон принимает такие решения, т. е. выбирает такую стратегию действий, которая с их точки зрения обеспечивает наибольший выигрыш или наименьший проигрыш.
Модели сетевого планирования применяются с целью сокращения сроков выполнения сложных проектов и других работ и оптимального использования предназначенных для этого ресурсов.
§3. Метод экономического анализа
При проведении системного анализа рассматриваются структурные части народного хозяйства: регионы, отрасли, объединения, предприятия.
Метод экономического анализа заключается в том, что происходит разделение экономического процесса или явления на составные части, и выявление взаимосвязи и влияния этих частей друг на друга и на ход развития всего процесса. Анализ позволяет раскрыть сущность такого процесса, определить закономерности его изменения в прогнозируемом (плановом) периоде, всесторонне оценить возможности и пути достижения поставленных целей.
Процесс экономического анализа подразделяется на следующие стадии:
- постановку проблемы, определение целей и критериев оценки;
- подготовку информации для анализа;
- изучение и аналитическую обработку информации;
- разработку рекомендаций о возможных вариантах решения проблемы и достижения целей;
- оформление результатов анализа.
В процессе экономического анализа акцент должен делаться на выявление резервов снижения издержек производства, определение эффективности использования производственных мощностей, финансовых и трудовых ресурсов. Необходимо также осуществлять анализ соответствия выпускаемой продукции спросу на нее.
При экономическом анализе возможно использование следующих методов: сравнение, группировка, индексный метод, балансовые расчеты, нормативный и экономико-математические методы (метод корреляционно-регрессионного анализа и др.).
§4. Конъюнктура рынка
Конъюнктура рынка – это совокупность конкретных экономических, социальных, организационных, политических, и других условий, определяющих в каждый данный момент соотношение спроса и предложения.
Экономический смысл конъюнктура – хозяйственная ситуация на рынке, возникшая под влиянием действующих процессов и явлений.
Исследование конъюнктуры рынка можно подразделить на два основных блока: изучение общехозяйственной конъюнктуры и изучение конъюнктуры конкретного товарного рынка, которые в зависимости от целей исследования можно проводить двумя путями:
· для выяснения тенденции и темпов развития конъюнктуры за какой-либо период, анализ конъюнктуры проводится путем изучения ее динамики за этот период;
· для определения конъюнктуры на текущую дату проводится анализ состояния конъюнктуры путем определения фазы экономического цикла и примерного места внутри фазы.
Важнейшей характеристикой эффективности функционирования рынка является степень сбалансированности структурно-объемного и качественно-ассортиментного спроса и предложения.
Тема 2. Определение потребительских свойств продукции и её качества
§1. Моделирование потребления
Функция полезности U(x1, x2) используется для определения оценки полезности каждого набора товаров X = (x1, x2) потребителем. Вектор X является планом потребления, составляющие которого, представляют собой количества потребляемой продукции различных видов.
Функция полезности имеет следующие свойства:
1) рост объёма потребления одного из товаров при неизменном объёме потребления другого увеличивает потребительскую оценку набора товаров;
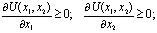
2) предельная полезность любого из товаров не возрастает, если объём его потребления растёт;
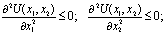
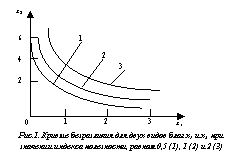
Для изучения личного потребления используется кривая безразличия, которая представляет собой совокупность потребительских наборов, обеспечивающих одинаковый уровень удовлетворения потребностей потребителя. В двумерной системе кривые безразличия U(x1, x2) соответствуют некоторому постоянному значению полезности U* = const. Если рассматривать не два вида благ, а N, то в такой многомерной системе постоянному значению индекса полезности будут соответствовать не кривые, а поверхности.
Для двух видов благ x 1 и x 2 кривые безразличия изображены на рис.1.
При приобретении покупателем на рынке каких-либо благ он вынужден учитывать их цену. Следовательно, возникает необходимость формализации условий, ограничивающих выбор потребителя. Таковыми являются доход (бюджет) потребителя и цены товаров.
Пусть бюджет потребителя равен R, а план потребления X = (x1, x2). Тогда R = RН + RП, где RН это часть, идущая на накопление, а RП – часть, расходуемая на потребление, т. е. на покупку будет тратиться сумма RП. Если цену первого товара обозначить p1, цену второго p2, а доход, идущий на приобретение товара – М, то множество наборов, которые являются доступными для потребителя, удовлетворяют следующему неравенству:
p1 x1 + p2 x2. £ М (1)
где p1 x1 – расход на x1 единиц товара 1; p2 x2 – расход на x2 единицы товара 2.
Среди множества доступных товаров, существуют такие наборы, которые стоят ровно М ден. ед. Для них неравенство (1) выполняется как строгое равенство:
p1 x1 + p2 x2. = М (2)
Это уравнение называется бюджетным ограничением, и представляет собой отрезок прямой в пространстве товаров.
Из (2) получаем
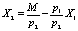 . (3)
. (3)
Из (3) видно, что наклон прямой определяется соотношением цен, а сдвиг её относительно оси X2 – величиной ![]() .
.
Рассмотрим рисунок 2.
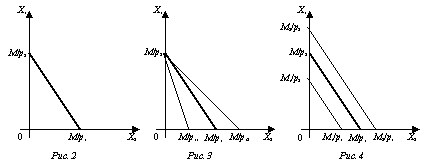

Если потребитель потратит весь доход на приобретение товара 1 в максимально возможном объёме, равном M/p1, то он не потратит ни одной единицы на приобретение товара 2, и, наоборот, в случае отказа от товара 1, он может приобрести M/p2 единиц товара 2. Следовательно, точки (0, M/p2) и (M/p1; 0) являются границами бюджетной линии.
Рассмотрим рисунок 3.
Если изменяется цена, например, на товар 1, то линия бюджетного ограничения сдвигается либо ближе к началу координат (при повышении цены товара 1 до p11), либо отодвигается в противоположную сторону (при понижении цены товара 1 до p12).
Рассмотрим рисунок 4.
При изменении дохода потребителя, бюджетная линия либо опускается вниз (если М уменьшается до М1), либо поднимается вверх (если М увеличивается до М2) параллельно исходной бюджетной линии.
§2. Задача оптимизации потребительского выбора
Математическая задача оптимизации потребительского выбора, основанная на гипотезах теории поведения потребителя имеет вид:
U = U(x1, x2) ® max; (4)
p1 x1 + p2 x2 £ M (5)
Решением такой задачи является определение потребительского набора (x1*, x2*), являющегося допустимым для потребителя и обеспечивающего максимально возможный уровень полезности. Стоимость этого набора должен быть не больше дохода М.
Задача оптимизации потребительского выбора является задачей математического программирования, где (4) – целевая функция, а (5) – допустимое множество. Т. к. для оптимальных точек ограничение (5) выполняется как строгое равенство, то решение задачи может быть найдено, нахождением условного экстремума (максимума) функции:
U = U(x1, x2) ® max; (6)
p1 x1 + p2 x2 = M (7)
Т. о. задача выбора потребителем набора с максимально возможной полезностью при заданных системе предпочтений, ценах и доходе сводится к решению задачи оптимизации потребительского выбора. Для решения этой задачи используется метод Лагранжа. Найденный оптимальный набор товаров потребителя X* характеризует спрос на рассматриваемые товары.
На изменение величины спроса на товары влияет изменение цен на товары и изменение дохода потребителя, поэтому возникает определённая зависимость, которую можно описать с помощью функций D1 и D2:
x1* = D1(p1, p2, M) и x2* = D2(p1, p2, M). (8)
Введённые функции называются функциями спроса Маршала.
При исследовании функций спроса можно оценить влияние изменения цен товара и изменения дохода на величину спроса. Для этого необходимо найти частные производные функций D1 и D2 по переменным p1, p2 и M.
При фиксации значений переменных p2 и M в функции x1* = D1(p1, p2, M) на некотором уровне, функция D1 превратится в функцию одной переменной, которая описывает зависимость величины спроса на товар 1 от его цены. График этой функции называется кривой спроса.
При фиксации значений переменных p1 и p2 получаем зависимость величины спроса на товар 1 от дохода М. График этой функции называется кривой Энгеля.
Для исследования зависимости уровня достигаемой полезности от всевозможных значений цен и дохода целесообразно заменить в функции полезности x1 и x2 на функции спроса x1* = D1(p1, p2, M) и x2* = D2(p1, p2, M). Полученная функция обозначается V(p1, p2, M) или V(p, M), (где p – вектор цен, p = (p1, p2)) и называется функцией косвенной полезности.
(вставить свойства функции с.65 мод. эк. проц. Грачёвой)
§3. Выбор потребителя при заданной полезности
Предположим, задана некоторая кривая безразличия и цены товаров. Из множества одинаково полезных наборов потребитель желает выбрать такой, который минимизирует его расходы при заданных ценах на товары. Математически данная задача записывается следующим образом:
m = p1 x1 + p2 x2. ® min; (9)
U(x1, x2) = u. (10)
Эта задача является задачей на нахождение условного экстремума и решается методом Лагранжа.
Геометрическая интерпретация данного метода:
Оптимальный набор товаров для задачи (9), (10) является точкой касания некоторой линии уровня целевой функции m(x1, x2) = p1 x1 + p2 x2 и нулевой линии уровня функции-ограничения G(x1, x2) = u – U(x1, x2).
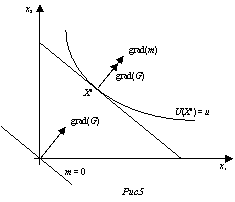

Т. о. оптимальный набор X0 = (x10, x20) решения задачи зависит от уровня полезности и соотношения цен на продукты, задающего наклон линий уровня линейной целевой функции.
Введём функции от цен и полезности. Обозначим их через x10 = H1(p1, p2, u) и x20 = H2(p1, p2, u). Эти функции называются функциями спроса Хикса. Они позволяют исследовать динамику спроса и минимальный расход на оптимальный потребительский набор m0 = p1 x10 + p2 x20 в зависимости от уровня полезности и цен. Для этого необходимо подставить функции спроса H1 и H2 в целевую функцию. Полученная функция называется функцией расходов и обозначается m = (p1, p2, u) или m(p, u) где p – вектор цен, p = (p1, p2).
(вставить свойства функции с.67 мод. эк. проц. Грачёвой)
§4. Оценка качества товара
При приобретении товаров покупатель в первую очередь должен быть уверен в их гарантированном качестве.
Под качеством понимается совокупность свойств товара, удовлетворяющих конкретные потребности потребителей в фиксированных условиях.
Оценка качества происходит различным показателям в зависимости от:
- цели рассмотрения;
- вида товара;
- стадии, на которой производится оценка качества;
- комплекса социальных и экономических факторов.
Методы определения показателей качества товара зависят от:
- стадии жизненного цикла;
- используемых средств.
Методы определения значений показателей качества товара в зависимости от используемых средств подразделяются на:
• экспериментальный, оцениваемый техническими измерительными средствами или основанный на обнаружении и подсчета количества событий;
• расчетный, по установленным теоретическим или эмпирическим зависимостям с использованием определенных параметров производятся необходимые вычисления;
• органолептический, определение качества товара на основе анализа восприятий органов чувств человека без применения технических и регистрационных средств;
• социологический, происходит сбор и анализ мнений фактических или возможных потребителей товара;
• экспертный, учитывающий мнения специалистов-экспертов.
Также возможно применение смешанных методов, например, при оценке комплексного показателя качества товара расчетным методом определение коэффициентов весомости единичных показателей происходит экспертным методом.
Для определения комплексного показателя качества товара (Р) вводится функция:
P = f(qi, bi, n),
где qi – i-й единичный показатель качества, i = 1…n; bi – коэффициент весомости i-го показателя; n – общее количество единичных показателей, по которым оценивается качество товара.
???????§3. Методы оценки уровня качества товара???????????????
Под уровнем качества товара понимается относительная характеристика качества, основанная на сравнении совокупности показателей качества данного товара с соответствующей совокупностью базовых показателей товара-аналога, перспективного или базового образца.
Под перспективным образцом понимается товар, совокупность показателей которого соответствует мировым стандартам или выше их или соответствует прогнозируемому экономически оптимальному на определенный период уровню качества товара данного вида.
Под аналогом подразумевается товар отечественного или зарубежного производства того же вида, конструктивного устройства, принципа действия, функционального назначения, масштабов производства и условий применения, что и сравниваемый товар.
В качестве аналогов рекомендуется выбирать объекты серийного и массового производства в количестве, как правило, не менее одного отечественного и одного зарубежного образца. Аналоги должны соответствовать передовым достижениям науки и техники. За базовые показатели могут быть приняты показатели отечественных и зарубежных стандартов.
Выбор метода определения уровня качества товара и состава базовых показателей зависит от цели оценки, т. е. от характера решений, которые нужно принять на основе полученных результатов. Схема оценки уровня качества товара приведена на рис. 1.
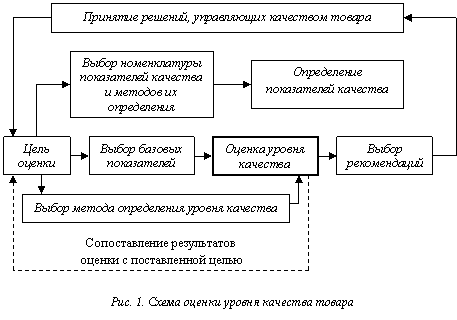

При сопоставлении результатов проведенной оценки с поставленной целью выясняют степень соответствия товара установленным показателям качества, характер отклонений отдельных показателей качества от соответствующих базовых показателей и целесообразность их изменения, необходимость корректировки номенклатуры оценочных показателей, способов их определения для получения более объективных оценок.
Оценка уровня качества конкретного товара может производиться дифференциальным и комплексным методами.
Оценка дифференциальным методом проводится главным образом для выявления отдельных показателей, существенно отличающихся от базовых показателей качества, и планирования их изменения в нужном направлении. Относительные показатели качества (К) определяются путем сопоставления единичных показателей качества товара (qi) с единичными базовыми показателями (qib) перспективного образца или аналога:
![]() , (1) или
, (1) или ![]() , (2)
, (2)
где i – порядковый номер показателя, i = 1…n.
Формула (1) применяется тогда, когда большее значение i-го показателя соответствует более высокому качеству товара (например, производительность, мощность), в то время как формула (2) применяется в случае, когда чем меньше абсолютное значение i-го показателя, тем качество товара лучше (например, уровень шума, уровень вибрации).
Если Кi > 1, то по i-му показателю качества анализируемый товар превосходит товар-аналог (базовый образец). Если Кi < 1, тогда по i-му показателю товар уступает товару-аналогу. В случае же если Кi = 1, то по i-му показателю качества анализируемый товар находится на уровне товара-аналога (базового образца).
Оценка комплексным методом производится тогда, когда уровень качества товара целесообразно охарактеризовать с помощью одного или нескольких обобщенных показателей. Относительный комплексный показатель качества определяется зависимостью:
![]() ,
,
где Q – комплексный показатель качества анализируемого товара; Qb – комплексный показатель качества перспективного образца или аналога.
Значения Q и Qb показателей определяются функциональными зависимостями:
Q = F(q1, q2, …, qn), Qb = F(q1b, q2b, …, qnb),
где n – количество единичных показателей, определяющих значение комплексного показателя качества.
В случаях, когда комплексный показатель не может быть выражен непосредственно через единичные показатели качества, вычисляют так называемый «средневзвешенный» комплексный показатель качества в виде свертки абсолютных значений единичных (частных) показателей (формула (3)) или их относительных значений (формула (4)).
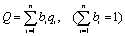
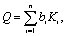
где bi – коэффициент весомости (значимости) i-го показателя качества.
Чем больше значение комплексного показателя Q рассчитанного по формуле (4), тем выше уровень качества этого товара.
На весомость показателя качества могут влиять социальные и экономические факторы, конъюнктура рынка, уровень производства и условия эксплуатации, особенности торговли. Коэффициенты весомости, как правило, определяются экспертным методом, но они могут быть вычислены и с помощью статистических методов.
§5. Оценка конкурентоспособности товара
Под аналогом подразумевается товар отечественного или зарубежного производства того же вида, конструктивного устройства, принципа действия, функционального назначения, масштабов производства и условий применения, что и сравниваемый товар.
При сравнении комплексных технических и экономических показателей товаров-аналогов производится оценка уровня их конкурентоспособности, причём показатель общей конкурентоспособности (Кк) определяется по формуле:
![]() ,
,
где Т – показатель конкурентоспособности по техническим показателям; Э – показатель конкурентоспособности по экономическим показателям,
Формула определения показателя конкурентоспособности по техническим показателям имеет вид:
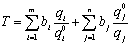 ,
,
где i – номер показателя качества, большее абсолютное значение которого соответствует более высокому уровню качества товара, i = 1…m; j – номер показателя качества, большее абсолютное значение которого соответствует более низкому уровню качества товара, j = 1…n; qi, qj – абсолютное значение i-гo и соответственно j-гo показателя качества анализируемого товара; qi0, qj0 – абсолютное значение i-гo и соответственно j-го показателя качества товара, принятого за базовый; bi, bj – коэффициенты весомости соответственно i-го и j-го показателей качества.
Для определения показателя конкурентоспособности по экономическим показателям используется формула:
 ,
,
где 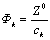 – доля k-го вида затрат ck в цене продажи Z0 базового товара (иначе, коэффициент весомости k-го вида издержек); ck – стоимостное выражение затрат на производство сравниваемого товара по k-му виду издержек; ck0 – стоимостное выражение затрат на производство базового изделия по k-му виду издержек.
– доля k-го вида затрат ck в цене продажи Z0 базового товара (иначе, коэффициент весомости k-го вида издержек); ck – стоимостное выражение затрат на производство сравниваемого товара по k-му виду издержек; ck0 – стоимостное выражение затрат на производство базового изделия по k-му виду издержек.
Товар является конкурентоспособным при Кk ³ 1.
§6. Зависимость цены продукции от её качества
Цена (в широком смысле) – это все субъективные или объективные затраты потребителя, связанные с приобретением товара, имеющего определённые качества.
Под качеством понимается необходимая потребителю совокупность всех вещественных и нематериальных элементов и свойств товара.
Уровень качества товара – это относительная характеристика качества, основанная на сравнении совокупности показателей качества данного товара с соответствующей совокупностью базовых показателей товара-аналога, перспективного или базового образца.
При определении зависимости между качеством и затратами на производство товара производитель стремится к максимизации отношения:
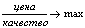
При определении зависимости между качеством и пользой от приобретаемого товара потребитель стремится минимизировать данное отношение:
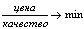 .
.
При этом возникает вопрос определения фирмой максимально возможного уровня качества товара (ТУmax) и соответствующую этому уровню цену (Цmax), и минимально допустимого уровня качества (ТУmin) и соответствующую минимальную цену (Цmin) в конкретных условиях.
Также возможна ситуация когда технический уровень остается неизменным ТУmax = TУmin = TУ, а цена колеблется от Цmax до Цmin.
Введём обозначения. Пусть величина М соответствует ситуации, когда соотношение между ценой и качеством выгодно для производителя, величина т соответствует ситуации, когда это выгодно для потребителя, которые определяются следующим образом:
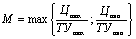 ,
,
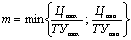 .
.
Рассмотрим величину т* = a1 М + a2 m, где a1 + a2 = 1; a1, a2 > 0.
Если a1 = 0, то т* = т и учитываются только интересы покупателя. Если a2 = 0, то т* = М, и в этом случае приоритет отдается интересам производителя. При a1 > 0 и a2 > 0 учитываются интересы обеих сторон, причем в большей или меньшей степени в зависимости от значений коэффициентов a1 и a2. (Следует иметь в виду, что приведенные рассуждения не учитывают спрос на товар.)
Таким образом, цена товара, как правило, есть функция от его качества (потребительских свойств).
Исследуем зависимость изменения цены товара от изменения его уровня качества (технического уровня).
Пусть k – качество товара, а Ц(k) – функция цены. Тогда производная функции Ц(k) будет выражать скорость изменения цены в зависимости от изменения уровня качества:
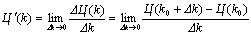 .
.
Зная скорость изменения цены, в некоторых случаях можно прогнозировать ценовую политику фирмы. Также можно учитывать тот факт, что потребители по многим товарам имеют более или менее ясное представление о приемлемой цене. Это можно расценивать, как область готовности покупателя заплатить за товар такую цену.
Одной из экономической модели поведения является рациональность, которая вынуждает взвешивать позитивные и негативные последствия, связанные с приобретением товара.
Пусть даны однородные товары А, В и С, которые воспринимаются как одинаковые с точки зрения качества, но цены на них различны (рис. 3).
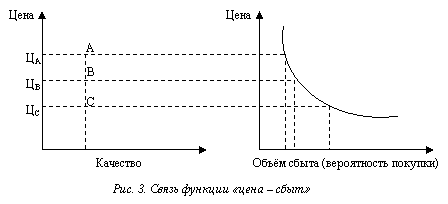

Согласно принципу рациональности выбирается товар с наиболее низкой ценой (товар С), т. е. с падением цены вероятность покупки возрастает. В микроэкономической теории цен эта связь формализована с помощью функции «цена – сбыт».
На практике иногда имеет место отклонение реального поведения потребителей от принципа рациональности. Например, тщеславие заставляет людей покупать более дорогие товары или при росте цен потребитель предполагает, что цена и дальше будет расти, и приобретает товар в большем количестве.
Тема 3. Планирование маркетинговой политики
§1. Планирование в маркетинговой деятельности
При планировании маркетинговой политики происходит определение различных альтернативных действий, а также выбор оптимальной альтернативы, которая позволяет получить наилучший результат в достижении поставленной цели.
Целенаправленный выбор альтернатив представляет собой принятие управленческого решения. Альтернативами могут быть:
- новые целевые области (товарные рынки);
- виды выпускаемой продукции;
- инвестиции в различные сферы деятельности фирмы и т. д.
После реализации (осуществлении) любой альтернативы возможен один или несколько последствий (результатов). Например, выручка от реализации товаров, издержки производства, доля удовлетворения спроса, прибыль, затраты на продвижение товара, доля рынка и др.
На результат реализации альтернативы могут оказывать влияние факторы, не подверженные (или частично подверженные) влиянию со стороны лица принимающего решения. Такое воздействие называется ситуацией внешней или окружающей среды.
На состояние внешней среды могут оказывать влияние следующие факторы:
- имеющаяся политическая обстановка (стабильная, нестабильная);
- поведение конкурирующих фирм (реактивное, нереактивное);
- социально-экономические условия (платежеспособный спрос, правительственное регулирование экономики и т. д.).
Состояния внешней среды в теории принятия решений называют гипотезами.
Обозначим через Аi (i = 1…m) – реализуемые альтернативы, которым соответствуют некоторые состояния окружающей среды Zj (j = 1…n); еij – ожидаемый результат при выборе альтернативы Аi и принятии гипотезы Zj. В результате можно записать функцию предпочтения, или функцию полезности f, т. е.:
еij = (Аi, Zj).
Значения функции f представляются в виде матрицы ожидаемых результатов, где также могут задаваться вероятности появления ситуаций внешней среды (гипотез) рj (j = 1…n), при принятии решений считаемые рисками.
Таблица 1. Матрица описания задач принятия решений в маркетинге
|
Альтернативы, Аi |
Состояния внешней среды (гипотезы) | |||
|
Z1 |
Z2 |
… |
Zn | |
|
А1 |
е11 |
е12 |
… |
е1n |
|
А2 |
е21 |
е22 |
… |
е2n |
|
… |
… |
… |
… |
… |
|
Аm |
еm1 |
еm2 |
… |
еmn |
|
Вероятности гипотез, pi |
p1 |
p2 |
… |
pn |
Определение. Альтернатива Ai – считается в общем случае доминирующей, если не существует никакой другой альтернативы Ak (k = 1…m и k ¹ i) со значением
еkj ³ еij (j = 1…n, k = 1…m) и еkj > еij (для наименьшей величины, соответствующей j), где ekj означает ожидаемый результат от применения альтернативы Аk при наступлении состояния внешней среды Zj.
Доминирующая альтернатива, имеющаяся в матрице решений, выбирается в качестве планового решения. При её отсутствии решение приходится принимать в условиях вероятностной определенности (риска) и неопределенности. В этом случае необходимо применять специальные принципы принятия решений (решающие правила) или критерии принятия решений.
§2. Методы решения задач планирования в условиях полной определенности
Существуют однокритериальные и многокритериальные методы выбора плановых решений.
1. Однокритериальные методы выбора. При выборе плановых решений задаются следующие величины:
• исходное множество альтернатив А = {Ai}, i = 1…m;
• оценки результатов выбираемых альтернатив f(Ai);
• критерий выбора: 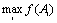 или
или 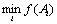 .
.
При выборе решения определяется однозначная связь между принятым решением Аi и его результатом f(Ai), т. е. определяется альтернатива А*, для которой f(А*) = mах f(Ai) или f(А*) = min f(Аi).
2. Многокритериальные методы выбора. Принятие решения при планировании маркетинговых действий в большинстве практических случаях сопровождается необходимостью учитывать не один, а несколько критериев. Все критерии при этом стремятся к максимуму (при стремлении к минимуму соответствующие критерии умножаются на (-1), причём решение при этом не изменится)
Для принятия решений составляется матрица исходных данных (табл. 2), в которой находится доминирующая альтернатива, принимаемая в качестве планового решения.
Таблица 2 Матрица исходных данных для многокритериальных методов выбора
|
Альтернативы, Аi |
Критерии (цели) | |||
|
Z1 |
Z2 |
… |
Zn | |
|
А1 |
е11 |
е12 |
… |
е1n |
|
… |
… |
… |
… |
… |
|
Аm |
еm1 |
еm2 |
… |
еmn |
Однако на практике доминирующие стратегии встречаются редко. Тогда применяются методы многокритериального выбора, причем решение должно быть наилучшим в определенном смысле.
В этом случае для модели, рассматриваемой экономической системы, выделяются существенные показатели качества альтернатив выбора, соответствующие поставленным целям. Данная проблема приводит к задаче векторной оптимизации, заключающейся в нахождении максимума вектор-функции:
F(x) = (f1(x), f2(x), …, fn(x)) ® ![]() ,
,
где D — область допустимых решений модели.
Однако в случае многокритериальной оптимизации возникают следующие проблемы:
1. Проблема выбора принципа оптимальности. В математическом отношении данная проблема эквивалентна задаче упорядочения векторных множеств, а выбор принципа оптимальности – выбору отношений порядка.
2. Проблема нормализации векторного критерия F(x). Частные критерии имеют различные единицы измерения, поэтому их необходимо привести к единому масштабу измерения, т. е. нормализовать (обычно приводят к безразличным величинам).
3. Проблема учета приоритета (степени важности) частных критериев. Часто для учета приоритета вводится вектор распределения важности или значимости критериев a = (a1, a2,…, an).
В задаче многокритериального выбора решение почти всегда ищется в области компромиссов или в области решений, оптимальных по Парето. Существует ряд методов решения многокритериальных задач, которые можно разбить на четыре группы:
1. Сведение многих критериев к одному путем введения весовых коэффициентов для каждого критерия (более важный критерий получает больший вес).
2. Минимизация максимальных отклонений от наилучших значений по всем критериям.
3. Оптимизация одного критерия (почему-либо признанного наиболее важным), а остальные критерии выступают в роли дополнительных ограничений.
4. Упорядочение (ранжирование) множества критериев и последовательная оптимизация по каждому из них.
В рассматриваемой постановке множество допустимых планов есть совокупность альтернатив D = {A1, A2, …, Am}, а значения критериев равны:
fj(Ai) = еij.
§3. Методы многокритериальной оптимизации к решению задач планирования
К методам многокритериальной оптимизации для решения задач планирования относятся:
- метод равномерной оптимальности;
- метод справедливого компромисса;
- метод свертывания критериев;
- метод главного критерия;
- метод идеальной точки;
- метод последовательных уступок (или пороговых значений);
- метод группировки критериев.
Метод равномерной оптимальности применяется в том случае, когда глобальное качество альтернативы представляет собой сумму локальных (частных) качеств, причём все критерии имеют одну и ту же единицу измерения, например, денежное выражение или безразмерные величины:
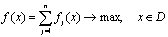 .
.
Главным недостатком метода является возможность компенсации малых значений некоторых критериев достаточно большими значениями других.
Метод справедливого компромисса применяется в случае, когда существуют разнообразные схемы, приводящие к такому методу, а также имеется тесная связь с решением в некооперативных играх:

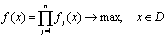 .
.
Для метода свертывания критериев каждому из критериев приписываются весовые коэффициенты (aj), определяющие предпочтения лица принимающего решения:
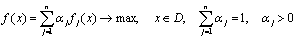 .
.
Для метода главного критерия определяется главный (наиболее важный из всех для ЛПР) критерий – f1(x), а также нижняя граница j-го критерия, устанавливаемая ЛПР – dj:
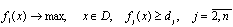 .
.
Для метода идеальной точки ищется план, удовлетворяющий условию равномерного сжатия:
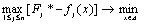 ,
,
где 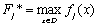 .
.
Метод последовательных уступок (или пороговых значений):
fk(x) ® max, x Î D,
fj(x) ³ Fj* – hj, j = 1…k–1; k = 2…n,
где hj – уступка по критерию fj(x), т. е. величина, на которую ЛПР согласен уменьшить значение данного критерия по сравнению с его максимальным значением.
Для метода группировки критериев предварительно вычисляются значения множества критериев на некотором оптимальном по Парето плане xº. Затем эти критерии разбиваются на три группы, первая из которых включает критерии, значения которых могут быть уменьшены по сравнению со значениями, вычисленными на плане хº, вторая состоит из критериев, значения которых желательно увеличить и третья включает критерии, значения которых не хотелось бы уменьшать по сравнению с достигнутыми на плане xº.
Далее отыскивается план уже в новой системе ограничений, который позволяет максимально увеличить значение критерия второй группы.
Однако прежде чем приступить к решению многокритериальной задачи, необходимо привести все критерии к одной единице измерения (обычно к безразмерному виду). Этот процесс называется нормализацией. Существуют различные методы нормализации, например, можно использовать следующий способ получения безразмерной формы критериев:
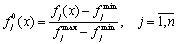 ,
,
где 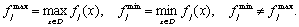
§4. Принятие маркетинговых решений в условиях неопределенности
Задачи планирования в большинстве случаев зависят от ряда заранее неизвестных и неуправляемых факторов, имеющих ту или иную степень неопределенности. Данная степень может быть как объективной, так и субъективной, зависящей от индивидуальных психофизических параметров ЛПР. В таких задачах внешняя среда может находиться в одном из возможных состояний Zj, j = 1…n, распределение вероятностей p(Zj) которого неизвестно. В отношении состояния внешней среды ЛПР может выдвигать только определённые гипотезы.
Поэтому, действуя в условиях неопределенности и невозможности получения дополнительной информации о неопределенных факторах, элементами описания ситуации планирования являются:
• множество допустимых стратегий (множество возможных альтернатив действий ЛПР) A = {A1, A2, …, Am};
• множество возможных состояний внешней среды (множество гипотез) Z = {Z1, Z2, …, Zn}.
Пусть на множестве отношений A ´ Z можно задать некоторую функцию полезности f (Ai, Zj), выступающую в качестве меры желательности или полезности соответствующей альтернативы. Для конечных множеств A и Z мера для оценки эффективности действий ЛПР (полезность исходов) представляется в виде матрицы, где каждое конкретное значение элемента матрицы eij = f(Ai, Zj) (см. табл. 1 §1) характеризует выбор i-й стратегии (альтернативы Аi) при состоянии внешней среды Zj.
Для выбора лучшей стратегии в условиях неопределенности имеется ряд специальных методов.
Согласно критерию максимина (принципа гарантированного результата, или критерия Вальда) в качестве оптимальной (наиболее эффективной) выбирается та альтернатива (стратегия), которая имеет наибольшее значение функции полезности среди наименее благоприятных состояний внешней среды. Для альтернативы А* критерием оптимальности является выполнение следующего соотношения:
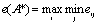 .
.
где eij – есть значение функции полезности при альтернативе Ai, i = 1…m и состоянии внешней среды Zj, j = 1…n.
Оптимальная альтернатива А*, выбранная по критерию Вальда, обеспечивает гарантированный выигрыш (успех в достижении цели) при наихудшем состоянии внешней среды для рассматриваемой фирмы.
Критерий Гурвица представляет собой комбинацию принципа гарантированного результата и принципа оптимизма. При описании данного критерия функция оптимальности имеет вид:
e(A*) = a e1(A) + (1 – a)e2(A),
где e1(A) – стратегия выбора альтернативы, характеризующая принцип гарантированного результата; e2(A) – принципа оптимизма; a – весовой коэффициент, a Î [0, 1].
Учитывая, что ![]() ,
, 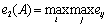 , общее выражение для принципа Гурвица будет иметь следующий вид:
, общее выражение для принципа Гурвица будет иметь следующий вид:
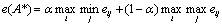 , или
, или 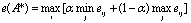
При использовании критерия Гурвица ставятся две гипотезы:
1. Среда находится с вероятностью a в самом невыгодном состоянии.
2. Среда находится с вероятностью (1 – a) в самом выгодном состоянии.
Различные предпочтительные альтернативы получаются в зависимости от значения весового коэффициента a, причем если a = 0, то получаем принцип оптимизма, если a = 1 – принцип гарантированного результата.
Например, при рассмотрении распределения товаров по рынкам, процентное соотношение этого распределения с использованием критерия Гурвица может быть вычислено по формуле:
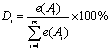 ,
,
где Di – доля товара, реализуемого на рынке Ai, выраженная в процентах; т – количество рассматриваемых рынков.
Критерий минимаксного сожаления (принцип Сэвиджа) характеризует потенциальные потери, которые фирма будет иметь, если выберет неоптимальное решение. Процедура выбора в этом случае производится в три этапа.
1. По конкретной альтернативе для каждого состояния внешней среды определяется максимальное значение функции полезности:
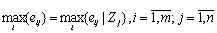 .
.
Результат, полученный для конкретного состояния внешней среды Zj, может быть наилучшим уровнем полезности.
2. Для каждой альтернативы на основании значений, вычисленных по предыдущей формуле, строится показатель:
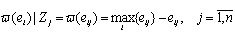 ,
,
который характеризует потенциальный риск или потерянную выгоду от выбора неоптимальной альтернативы. В результате этого действия формируется матрица потенциальных потерь.
3. Используя полученную матрицу потерь (матрицу сожалений) на предыдущем этапе, производится выбор стратегии с наименьшим показателем риска:
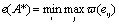 .
.
Данный критерий минимизирует возможные потери при условии, что состояние внешней среды наихудшим образом отличается от предполагаемого.
Критерий Лапласа применяется, в том случае, когда состояния внешней среды неизвестны, но их можно считать равновероятными, т. е.
p1 = p2 = … = pn = ![]() .
.
Решающее правило в этом случае имеет следующий вид:
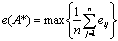 .
.
Практические рекомендации по применению рассмотренных критериев (принципов).
1. Критерий Вальда лучше всего использовать тогда, когда фирма желает свести риск от принятого решения к минимуму.
2. Коэффициент в критерии Гурвица выбирается из субъективных соображений: чем опаснее ситуация, тем больше ЛПР желает подстраховаться.
3. Критерий Сзвиджа удобен, если для предприятия приемлем некоторый риск.
4. Критерий Лапласа может быть применен, когда ЛПР не может предпочесть ни одной гипотезы.
Тема 4. Методы оптимизации маркетинговых затрат
§1. Реклама
Необходимым требованием при планировании рекламы является подготовка рекламного бюджета и распределение его по различным средствам рекламы. Причём величина бюджета и его распределение должны покрывать все расходы на рекламу за счёт увеличения торгового оборота, а также получение максимально возможной прибыли. На рис. 3 показана взаимосвязь рекламы и прибыли.
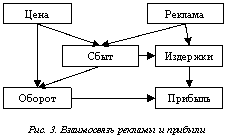

При формировании бюджета следует обращать особое внимание на характер кривых реакций на маркетинговую коммуникацию. Кривые реакций имеют следующие свойства:
· функция реакции на рекламу не линейна, т. к. величина спроса (сбыта) товара или услуги проходит через восприятие и насыщение, которые связаны с явлениями инерции или защиты, восприятия или усталости;
· наклон кривой реакции зависит от качества коммуникации (канал, содержание и т. п.);
· распределение во времени эффекта коммуникации (особенно рекламы), характер которого зависит от типа товара, выбора канала рекламируемого товара. Благодаря динамическому эффекту рекламу можно рассматривать как инвестицию, обеспечивающую товару стабильный спрос длительное время;
· влияние рекламы также зависит и от других факторов, таких как цены, системы сбыта и др. Связь между этими факторами имеет свойство мультипликативности.
Рассмотрим несколько методов установления рекламного бюджета.
1. Определение оптимального бюджета
Предположим рынок монополистический, и спрос на продукцию не расширяется. Тогда функция спроса Q, зависящая от расходов на рекламу товара С описывается выражением:
Q = a · C e,
где e – эластичность спроса по рекламе; а – константа.
Прибыль фирмы в этом случае определяется как
П = (Ц – Спер) ´ Q – C – Cпост,
где Ц, Спер, Спост – соответственно цена, переменные и постоянные издержки.
Условие оптимальности имеет вид:
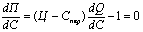 .
.
Умножим обе стороны этого уравнения на ![]() , тогда получим искомое выражение для условия оптимизации:
, тогда получим искомое выражение для условия оптимизации:
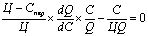 .
.
Преобразуем полученное выражение и получим следующие решающие правила:
• процент расходов на рекламу от выручки
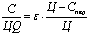 ;
;
• оптимальный бюджет
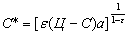 ,
,
где а = Q/Ce, 0 < e < 1.
Полученные правила используются для проверки избыточности или недостаточности текущего уровня бюджета.
2. Модель Видейла и Волфа
В данной модели устанавливается связь между объемом продаж или выручкой и расходами на рекламу. Соотношение этой зависимости имеет вид:
 ,
,
где ![]() – рост продаж; b – предельная прибыль от рекламы при n = 0; С – расходы на рекламу; n – объем продаж марки товара или фирмы; N – уровень насыщения продаж; l – уровень удерживания продаж.
– рост продаж; b – предельная прибыль от рекламы при n = 0; С – расходы на рекламу; n – объем продаж марки товара или фирмы; N – уровень насыщения продаж; l – уровень удерживания продаж.
Эта модель роста продаж ![]() в течение определенного периода представляет собой произведение:
в течение определенного периода представляет собой произведение:
• предельной прибыли на единицу затрат на рекламу при нулевых продажах (b) и общей суммы расходов на рекламу в рассматриваемый период (эффект реакции);
• скорректированный уровень насыщения продаж в зависимости от доли потенциального рынка, которую может завоевать данный товар дополнительно (эффект насыщения);
• уменьшенный объем продаж на долю продаж в данный период времени, которая будет потеряна под влиянием эффекта обеспечения, старения или забывания при прекращении всякой рекламы (динамический эффект).
Данную задачу можно также сформулировать в терминах бюджета. Для этого приведенное выше соотношение нужно решить относительно рекламного бюджета С.
3. Модель ADBUDG (Литтла)
Данная модель ориентирована на стабильный рынок с нерасширяемым спросом, где реклама является функцией роста продаж или доли рынка. Ожидаемая доля рынка в этом случае описывается соотношением:
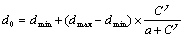 ,
,
где dmin – минимальная доля рынка, ожидаемая в отсутствие рекламы; dmax – максимальная доля рынка, ожидаемая при очень высоком уровне расходов на рекламу; С – эффективные расходы на рекламу (скорректированные с учетом качества рекламы); g – коэффициент чувствительности функции реакции; а - константа.
Здесь ожидаемая доля рынка включает в себя:
• минимальную долю рынка, т. е. долю рынка при нулевой рекламе (эффект снижения);
• часть максимального изменения доли рынка под воздействием рекламы (эффект реакции).
Уровень реакции в данном случае зависит от коэффициента интенсивности рекламы, задаваемого двумя параметрами:
1) коэффициентом g, определяющим характер функции реакции;
2) коэффициентом а, характеризующим ослабление функции реакции (при максимальной и при нулевой интенсивности рекламы он стремится соответственно к 0 и к 1).
Планирование рекламы заключается в распределении финансовых ресурсов по отдельным направлениям, причём в первую очередь распределение идёт по тем средствам рекламы, которые обещают наибольший успех в деятельности фирмы. Однако здесь возникает проблема получения данных. Необходимо определить количество лиц, с которыми устанавливались контакты, особенно с целевыми группами, причём распределение рекламного бюджета считается оптимальным, если иным путем невозможно добиться более эффективного контакта с объектами рекламы.
При распределении рекламного бюджета за основу берётся «критерий тысячной контактной цены ТКЦ», рассчитывающийся так, что одной демонстрацией по средству рекламы охватывается тысяча человек:
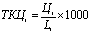 ,
,
где Цi – цена демонстраций в i-м средстве рекламы; Li – численность зрителей, увидевших демонстрацию рекламы в i-м средстве.
В первую очередь финансовые средства распределяются тому объекту рекламы, который имеет наименьший ТКЦ, далее – с чуть более высоким критерием и т. д. до тех пор, пока данный рекламный бюджет не будет полностью исчерпан. При таком распределении бюджета охватывается наибольшее число контактов.
Одним из недостатков критерия тысячной контактной цены является неопределённость того, сколько человек охвачено рекламой.
Критерием качества рекламной компании является эффективность рекламы, анализ которой проводится как перед рекламной компании, являющимся прогнозом эффективности, так и после неё, выполняющим контрольную функцию.
§2. Системы и каналы товародвижения и сбыта продукции
Сбытовая деятельность фирмы заключается в определении путей, по которым продукция фирмы через рынок попадает к потребителю.
Фирма-производитель может самостоятельно осуществлять сбыт своей продукции или привлекать для этого посредников, торговцев. С помощью посредников возможно сокращение количества прямых контактов производителей с потребителями товаров.
Если фирма организует самостоятельно сбыт продукции, то она должна иметь собственную систему сбыта. На рис. 1 представлена собственная система сбыта, и подразделения службы сбыта.
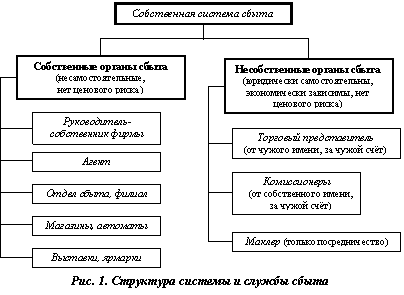

Некоторые пояснения к рисунку 1.
· Отдел сбыта и филиалы на местах обращаются к своим потенциальным клиентам с помощью каталогов, проспектов, характеризующих продукцию фирмы, и т. д. и участвуют в договоренностях с потребителями продукции об условиях продаж.
· Агенты – служащие с правом или без права заключения договора; их сильная сторона – хорошее знание товара.
· Некоторые производители имеют собственные магазины, могут создаваться временные магазины.
· Торговые представители – местные самостоятельные торговцы, работающие постоянно в определенном районе сбыта.
· Комиссионеры выступают, в отличие от торговых представителей, по отношению к третьим лицам от собственного имени, но работают за чужой счет.
· Маклеры способствуют заключению договоров, они собирают предложения и запросы, помогая тем самым заключать договора о сбыте продукции.
Подразделения собственной системы сбыта не связаны с ценовым риском, так как вся их деятельность осуществляется за счет средств фирмы.
При посреднической системе сбыта фирма – производитель продукции работает с юридически самостоятельными торговыми фирмами, которые продают товары от собственного имени и за свой счет, т. е. с ценовым риском. Но продавец экономически связан с производителем особыми отношениями – сбытовыми связями. Различают следующие виды сбытовых связей:
1. Вертикальная сбытовая связь. Продавец обязуется перед производителем не продавать товар определенному третьему лицу.
2. Согласование сбыта. Производитель обязуется перед продавцом использовать определенные каналы сбыта, например поставку товара тем продавцам, которые соответствуют определенным нормам; производитель ограничивает поставку нескольким продавцам в определенном районе.
3. Согласование заказов. Продавец обязуется перед производителем не иметь связи с третьими лицами. Приметы этому – дилеры и франчайзинг.
Дилеры заключают с производителем товара договор на исключительный заказ его товара. Наряду с прочими льготами (например, кредиты и т. д,) дилер может получить право использовать товарный знак производителя.
При франчайзинговой системе сотрудничество с продавцом осуществляется не только через товар или товарную группу, но и в рамках маркетинговой концепции. Существует возможность передавать собственные филиалы и магазины в франчайзинговые предприятия. Такое объединение способствует росту капитала и тем самым оборота. Однако укрепление сбытовых связей может способствовать ограничению конкуренции и росту монополизации.
Перед фирмой – производителем всегда стоит проблема выбора: осуществлять сбыт продукции через собственную сбытовую сеть или обращаться к оптовикам, розничным продавцам или непосредственно к конечным потребителям. Таким образом, необходимо решить, что выгоднее: прямой сбыт непосредственно конечным потребителям или косвенный сбыт через оптовую или розничную торговлю.
Каждый канал сбыта имеет свои достоинства и недостатки, а, следовательно, и области наилучшего использования.
Если фирма выбирает прямой путь, то она экономит на товарной наценке, но упускает услуги, предлагаемые торговлей:
• ценовой риск, связанный с реализацией продукции;
• часть складских операций, связанных с хранением продукции;
• замена рекламы производителя на более качественную рекламу торговли;
• дополнительные сервисные услуги;
• облегчение изготовителю специализации, самостоятельно формируя ассортимент.
Торговля получает свой доход за счет экономии затрат на сделку.
Прямой сбыт обычно используется в сфере производства оборудования и для оптовых покупателей. Часто прямой сбыт осуществляется через посредников. Прямой сбыт может осуществляться с личным консультированием.
§3. Модели отгрузки товаров фирмы через собственную сбытовую сеть
Существует множество моделей, подстраивающих производство и хранение продукции, производимой фирмой, под своевременность доставки продукции потребителям и др. Они описывают взаимосвязь фирмы через свои склады (базы), магазины с потребителями продукции с использованием различных видов транспорта: автомобильного, железнодорожного, воздушного, морского, речного и в сочетании друг с другом. В модели может включаться время доставки продукции.
Наибольшее распространение получила модель обычной транспортной задачи: найти оптимальные транспортные потоки при заданной конфигурации транспортной сети и заданных объемах производства и потребления продукции. Эта модель формулируется как закрытая (спрос сбалансирован с производством) и открытая (имеет место несоответствия спроса и производства). В модель могут вводиться дополнительные ограничения, связанные с производственно-технологическими условиями взаимосвязи фирмы-производителя с потребителями. Здесь предлагается модель управления сбытом продукции фирмы, описывающая наиболее важные требования в существующих российских условиях, предъявляемые к потребителям продукции фирмы, например, своевременность перевода денежных средств потребителями товаров.
Эта модель формируется следующим образом.
Пусть m, n – первый и последний дни рассматриваемой декады; T – последний день месяца; Nik – объем продукции i-го вида, который должен быть поставлен в территорию k (например, город) в рассматриваемую декаду, i = 1, …, r; k = 1, …, K; аi – запас продукции i-го вида на начало декады, i = 1, …, r; аit – объем продукции i-гo вида, выпускаемой в день t, i = 1, …, r; t = m, …, n; bi – трудоемкость упаковки единицы i-го вида продукции; Вi – эффективный фонд времени на упаковочных работах в день t, t = p, …, n; Цi – цена единицы продукции i-го вида, i = 1, …, r; рkd – вероятность получения денежных средств от потребителя k в течение d дней после отгрузки, k = 1, …, K; d = 1, …, 30; хikt – объем продукции i-го вида, отгружаемой k-й территории в день t, i = 1, …, r; k = 1, …, K; t = m, …, n.
Тогда модель можно записать следующим образом:
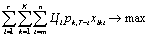 ; (1)
; (1)
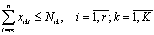 ; (2)
; (2)
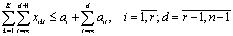 ; (3)
; (3)
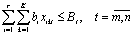 ; (4)
; (4)
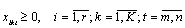 . (5)
. (5)
Рассмотрим постановку задачи. Начнем с целевой функции (1). Продукция объемом xikt оплачивается потребителем до конца месяца, т. е. в течение промежутка Т – t (вероятность этого равна рк,T-t), либо не оплачивается (вероятность чего равна 1 – рk,T-t). Следовательно, Цi pk,T-t xikt есть средняя сумма денежных средств, получаемых фирмой за отгрузку продукции xikt.
Ограничения (2) меняются в зависимости от того, для какой декады рассматривается модель. Для последней декады ограничения приобретают вид строгих равенств, правые части которых представляют собой неудовлетворенные заявки; для остальных они имеют вид неравенств. Величина Nik корректируется каждую декаду. При этом предполагается, что график выпуска продукции построен с учетом заявок.
Ограничения (3) увязывают отгрузку с графиком выпуска продукции и наличием ее на начало декады. Предполагается, что продукция, выпущенная в день t, может быть отгружена не раньше дня t + 1. Ограничения (4) и (5) очевидны.
Хотя подекадное планирование в общем случае не дает оптимального месячного графика сбыта, положение все же может быть улучшено, если учитывать ограничения (2) – (5) на ближайшие один-два дня без оптимизации суммы реализации.
Тема 5. Моделирование ценовой политики
§1. Выбор целей ценовой политики
Приступая к ценообразованию, руководство фирмы (предприятия) должно, прежде всего, определить, каких целей оно желает достичь посредством продажи данного товара. Наиболее существенными целями, достижению которых призвано служить ценообразование, являются следующие:
1. Обеспечение выживаемости фирмы. Такую цель ставят предприятия, которые сталкиваются на рынке с острой конкуренцией, либо имеют избыточные мощности, либо резко снизили объем продаж товара вследствие изменившихся желаний покупателей. Чтобы обеспечить сбыт товаров, они зачастую снижают цены в надежде на положительную ответную реакцию потребителей. Фирма может продолжить свою деятельность, пока цена покрывает издержки производства. Однако продолжение существования фирмы в таких условиях может рассматриваться только как краткосрочная цель.
2. Позиционирование товара на целевом рынке. Такая цель ставится при внедрении товара на целевой рынок. Высокая цена обычно связана с высоким качеством или престижем товара. Низкая цена устанавливается, когда фирма желает вступить на рынок более эффективно.
3. Краткосрочная максимизация прибыли. Многие фирмы, проводя ценовую политику, стремятся максимизировать текущую прибыль. Для этого определяются издержки и предварительный спрос по каждому ценовому варианту, из которых выбирается альтернатива, приносящая в краткосрочной перспективе максимальную прибыль. Однако реализация данной цели связана с проблемами оценки спроса и издержек. При этом упор делается на краткосрочное получение прибыли и не учитывает долгосрочную перспективу.
4. Краткосрочная максимизация оборота. Если товар производится корпоративно и в связи с этим сложно определить структуру издержек, то некоторые фирмы устанавливают цену, обеспечивающую максимизацию оборота. В этом случае достаточно определить функцию спроса. Реализовать данную цель относительно несложно путем установления в сфере сбыта процента комиссионных от объема сбыта. Существует мнение, что в случае максимизации текущих доходов (оборота), можно максимизировать прибыль и долю рынка в долгосрочной перспективе.
5. Максимальное увеличение сбыта (завоевание лидерства по показателю рыночной доли). Фирмы, преследующие эту цель, полагают, что увеличение сбыта приведет к снижению издержек единицы товара и, в конечном счете – к увеличению прибыли. При этом цена устанавливается как можно ниже. Такой подход называют «ценовая политика наступления на рынок». Добиваясь лидерства по показателю доли рынка, можно достичь положительного результата только при наличии ряда условий, а именно: чувствительность рынка к ценам очень велика; можно снизить издержки производства и распределения; конкуренты не предпримут еще большего снижения цен.
6. Завоевание лидерства по качеству товара. Фирма может поставить целью добиться, чтобы ее товар был самым высококачественным из всех предлагаемых на рынке. Это требует установления высокой цены на данный товар, чтобы покрыть большие издержки, связанные с повышением качества и необходимыми для этого НИОКР.
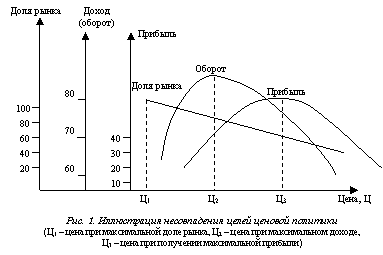

Перечисленные цели ценовой политики соотносятся между собой определенным образом, причем они не являются единственными и не всегда совпадают по направлению. Их достижение происходит в разное время и при различной цене. Это можно показать графически (рис. 1).
§2. Ценовая политика
При установлении цен фирма исходит, по меньшей мере, из учета трех факторов:
1. Цены должны превышать себестоимость, так как лишь в этом случае может быть получена прибыль.
2. Цены должны учитывать поведение покупателя по отношению к предлагаемой цене.
3. Цены должны учитывать поведение конкурентов на рынке товаров.
При учете первого фактора ценовая политика ориентируется на издержки, при учете второго и третьего факторов, напротив, учитывает поведение спроса и конкурентов, ориентируется на рынок.
1. Ценовая политика, ориентированная на издержки
На практике установление цен часто осуществляется по принципу: «себестоимость плюс соответствующая прибыль». Особенно это относится к торговым фирмам, которые рассчитывают прибыль в процентах от себестоимости.
Многие фирмы и промышленные предприятия следуют в ценообразовании этому принципу не в последнюю очередь, потому что относительно легко можно определить себестоимость единицы продукции и найти понимание у заказчиков «приемлемой» прибыльной наценки. Однако против этого достоинства имеются серьезные возражения. Установление таких цен связано со значительным риском. Это обусловлено тем, что желаемый объем сбыта и рассчитанная цена, как правило, на рынке оказываются не соответствующими друг другу (рис. 2).


Спрос на рынке развивается согласно функции спроса (рис. 2), а именно:
• если фирма-производитель устанавливает выпуск и цену равными N1 и Ц1 или NK и ЦK, то ее ожидания оправданы — спрос «подтягивается» и реализуется прибыльная наценка;
• если фирма-производитель устанавливают выпуск и цену выше точки А или ниже В, то ее ожидания не оправдываются – спрос отстает и прибыль исчезает;
• если фирма-производитель выбирает в качестве функции спроса комбинацию выпуска и цены между А и В, например С, то ее ожидания перевыполняются – спрос оказывается выше (NС2 вместо NС1) или может быть удовлетворен при более высокой цене ЦС1 вместо ЦС2 В любом случае увеличивается возможная прибыльная наценка.
Отсюда следует: желаемый объем сбыта и рассчитанная цена, как правило, на рынке оказываются не соответствующими друг другу (исключение А и В), В случае «приятного сюрприза» (точка С) не исключено, что существует еще более прибыльная, чем выбранная, комбинация.
Следовательно, ценообразование следует проводить исходя не из затрат, а из спроса, так как практически он определяет конечный результат.
С течением времени за счет приобретения опыта производства удельные затраты для данного объема производства обычно снижаются. Соответственно при установлении цен, ориентированных на затраты, сначала должна быть высокая цена, затем более низкая, т. е. должна использоваться стратегия «снятия сливок». Тем не менее, это не самая прибыльная цена. Более предпочтительной может оказаться политика, при которой сначала отказываются от покрытия затрат ("цена вхождения в рынок»), чтобы быстро достичь большого объема продаж и тем самым укрепить собственное положение на рынке, а также приобрести возможность получения прибили в будущем. Следовательно, с помощью «стратегии проникновения» осуществляются инвестиции в освоение рынка.
Таким образом, принцип, ориентированный на затраты ценовой политики, не подходит к стратегии проникновения.
2. Ценовая политика, ориентированная на рынок
В противоположность ценовой политике, ориентированной на затраты, существует ценообразование, которое учитывает возможности и границы рынка и при этом стремится максимизировать прибыль фирмы. Ее конкретная величина зависит от конкуренции и контроля за ценами федеральных органов надзора.
Ценовая политика, ориентированная на рынок, в значительной степени зависит от того, какой рассматривается рынок: совершенный (моногенный) или несовершенный (гетерогенный).
Для совершенного рынка характерно:
• все участники рынка имеют полное представление о рыночной ситуации;
• приспособление к изменившимся рыночным условиям осуществляется с максимально возможной скоростью;
• все продавцы на рынке оцениваются одинаково хорошо;
• все участники рынка стремятся извлечь на рынке свои выгоды: продавцы хотят получить максимальную прибыль, а покупатели получить от сделки максимальную полезность.
Следствием этого является одинаковый уровень цен у всех продавцов. Если один из них поднимет цену, то об этом узнают все покупатели и обратятся за покупкой к конкуренту. Поэтому ему не остается ничего иного, как снова ее снизить. На совершенном рынке все процессы приспособления протекают быстро, не возникает отличий в ценах, отсутствуют перемещения покупателей между продавцами. Примером совершенного рынка является рынок капиталов. На фондовом рынке отсутствуют курсовые разницы между различными биржевиками на акции определенного предприятия.
Как правило, рынки несовершенны и ценовая политика должна ориентироваться на различия в ценах продавцов.
§3. Методы ценообразования
Изучить самостоятельно (см. дисциплину «Моделирование ценообразования в рыночной экономике»)
Тема 6. Производственные системы
§1. Производственные системы и их структура
Производственный процесс.
Производственный процесс – основа деятельности любого предприятия, представляет собой совокупность отдельных процессов труда, направленных на превращение сырья и материалов в готовую продукцию заданного количества, качества, ассортимента и в установленные сроки. Содержание процесса производства оказывает определяющее воздействие на построение предприятия и его производственных подразделений.
Производственный процесс включает ряд технологических, информационных, транспортных, вспомогательных, сервисных и других процессов.
Классификация производственных процессов
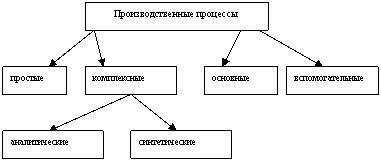
При простых производственных процессах в ходе последовательного воздействия на однородные предметы труда производят одинаковые продукты. В данном случае технология предписывает как строгую пространственную ориентацию рабочих мест, так и временную последовательность операций.
При аналитических производственных процессах предмет труда также однороден. Однако в ходе выполнения отчасти одинаковых операций производят неодинаковые продукты, т. е. из одного вида сырья получают несколько видов продукции.
При аналитическом процессе один заготовительный цех передает свои полуфабрикаты в несколько обрабатывающих и выпускающих цехов, специализирующихся на изготовлении различного рода продукции. В этом случае предприятие производит значительное число различных видов продукции, имеет большие и разветвленные связи по сбыту, как правило, здесь развиты побочные производства.
При синтетических производственных процессах различные простые детали изготавливают путем путём различных операций над разными предметами труда, а затем из них составляют сложные блоки, узлы, т. е. производственный процесс образуется в ходе различных но связанных в единый комплекс частичных процессов.
Производственные процессы бывают основные и вспомогательные. К основным относятся процессы, которые непосредственно связаны с изменением геометрических форм, размеров, внутренней структуры обрабатываемых предметов и сборочные операции. Вспомогательными являются процессы, которые непосредственно не связаны с предметом труда и призваны обеспечивать нормальное, бесперебойное функционирование основных процессов. К ним относится, например, изготовление инструмента для собственных нужд, производство энергии для собственных нужд, контроль качества и др.
Методы рациональной организации производственного процесса.
В зависимости от характера движения предметов труда различают поточный (непрерывный), партионный, единичный методы организации производственных процессов.
Поточное производство по ходу технологического процесса характеризуется непрерывным и последовательным движением предметов труда от одной операции к другой.
При партионном и единичном (прерывном) методах обрабатываемый продукт после каждой операции выключается из технологического процесса и находится в ожидании следующей операции. В этом случае относительно велики длительность производственного цикла и размеры незавершенного производства и оборотных средств, требуются дополнительные площади для хранения полуфабрикатов.
Наиболее прогрессивным методом организации производственного процесса считается поточный метод. Основными его признаками являются:
· высокая степень непрерывностей;
· расположение рабочих мест по ходу технологической обработки;
· высокая степень ритмичности.
Организационный базой поточного метода служит поточная линия, имеющая такие наиболее важные параметры, как такт и темп потока.
Тактом потока τ называется среднее расчетное время, по истечении которого в поток запускается или с потока выпускается одно изделие или транспортная партия изделий
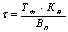 ,
,
где ТФ – фонд рабочего времени за расчетный период (смена, сутки и т. д.);
КИ – коэффициент использования оборудования, учитывающий простои и перерывы в работе;
ВП – объем планируемой продукции за расчетный период в натуральных единицах (штуках, метрах и т. д.).
Темп потока σ характеризует интенсивность труда работающих и определяется по формуле
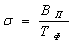 .
.
Принципы рациональной организации производственного процесса.
На любом предприятии организация производственных процессов базируется на рациональном сочетании в пространстве и во времени основных, вспомогательных и обслуживающих процессов. Однако при всем многообразии форм этого сочетания производственные процессы подчинены общим принципам.
Принципы рациональной организации можно разделить на три категории:
· общие, не зависящие от конкретного содержания производственного процесса;
· специфические, характерные для конкретного процесса.
Перечислим общие принципы.
Специализация – означает разделение труда между отдельными подразделениями предприятия и рабочими местами и их кооперирование в процессе производства.
Пропорциональность – обеспечивает равную пропускную способность разных рабочих мест одного процесса, пропорциональное обеспечение рабочих мест информацией, материальными ресурсами, кадрами и т. д.
Пропорциональность определяется по формуле
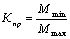 ,
,
где Мmin – минимальная пропускная способность, или параметр рабочего места в технологической цепи (например, мощность, разряд работ, объем и качество информации и т. п.);
Мmax – максимальная способность.
Непрерывность – предусматривает максимальное сокращение перерывов между операциями и определяется отношением рабочего времени к общей продолжительности процесса
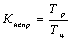 ,
,
где Тр – продолжительность рабочего времени;
Тц – общая продолжительность процесса, включающая простои и пролёживания предмета труда между рабочими местами, на рабочих местах и т. д.
Параллельность – характеризует степень совмещения операций во времени. Виды сочетаний операций: последовательное, параллельное и параллельно - последовательное.
Коэффициент параллельности можно вычислить по формуле
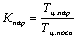 ,
,
где Тц. пар, Тц. посл - продолжительность процесса соответственно при параллельном и последовательном сочетании операций.
Прямоточность – обеспечивает кратчайший путь движения предметов труда, информации и т. п.
Коэффициент прямоточности можно определить по формуле
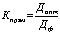 ,
,
где Допт – оптимальная длина пути прохождения предмета труда, исключающего лишние звенья, возвраты на прежнее место;
Дф – фактическая длина прохождения предмета труда.
Ритмичность – характеризует равномерность выполнения операций во времени.
Коэффициент ритмичности рекомендуется вычислять как
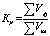 ,
,
где Vф – фактический объем выполненной работы за анализируемый период (декада, месяц, квартал) в пределах плана; Vпл – плановый объем работ.
Техническая оснащенность – ориентирована на механизацию и автоматизацию производственного процесса, устранение ручного, монотонного, тяжелого, вредного для человека труда.
Гибкость – заключается в необходимости обеспечивать быструю переналадку оборудования в условиях часто меняющейся номенклатуры производства. Наиболее успешно реализуется на гибких производственных системах в условиях мелкосерийного производства.
Одним из путей улучшения перечисленных принципов рациональной организации производственных процессов является увеличение повторяемости процессов и операций. Наиболее полная их реализация достигается при оптимальном сочетании следующих факторов:
· масштаб производства;
· сложность номенклатуры и ассортимента выпускаемой продукции;
· характер действия технологического и транспортного оборудования;
· физическое состояние и форма исходных материалов;
· характер и последовательность технологического воздействия на предмет труда и т. д.
§2. Технологии производства и их представление в экономико-математических моделях
Введем следующую систему обозначений:
i- индекс пункта производства, i = 1,2,..., т ;
j- индекс пункта потребления, j = 1,2,..., п ;
аi - максимально возможная мощность в i-м пункте производства;
bj - потреби ость j-го пункта потребления;
tij - затраты на перевозку единицы продукта из i-го пункта производства Bj-й пункт потребления;
si - затраты на производство единицы продукта в i-м пункте нового строительства (расширения или реконструкции действующего предприятия);
хij - объем перевозок из i-го пункта производства ву-й пункт потребления;
хi - размер производства в i-м пункте.
Требуется найти значения величин хij и хi, минимизирующих суммарный объем затрат на производство и доставку продукции
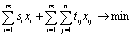 (4.33)
(4.33)
при выполнении следующих условий:
· суммарный ввоз продукции в каждый из пунктов потребления должен быть равен его потребностям
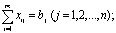 (4.34)
(4.34)
· суммарный вывоз продукции из каждого пункта производства должен быть равен размеру производства, а последний, в свою очередь, не может превосходить максимально возможный предел
 (4.35)
(4.35)
· объемы перевозок по всем возможным коммуникациям и размеры производства в каждом из пунктов должны быть неотрицательны
xij ³ 0 (i = 1, 2, …, m; j = 1, 2, …, n) (4.36)
xi ³ 0 (i = 1, 2, …, m). (4.37)
· Учитывая условие (4.35), перепишем критерий оптимальности (4.33)
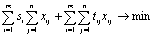 (4.38)
(4.38)
· или, проведя несложные преобразования,
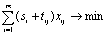 (4.39)
(4.39)
Иными словами, искомые в процессе решения перспективные производственные мощности предприятий могут принимать не любые значения на всем интервале изменения мощности (непрерывность), а лишь некоторые, строго определенные значения, т. е. в этом случае имеем задачу развития и размещения с дискретными (целочисленными) переменными.
Для записи модели с дискретными переменными и нелинейной зависимостью удельных производственных затрат от мощности дополнительно к ранее использованным введем следующие обозначения:
k – индекс типового проекта; число используемых типовых проектов для различных пунктов производства неодинаково, так что k = 1,2.....Кi,
Aik – мощность предприятия в i - м пункте производства по k-му типовому проекту;
ji(xi) – функция удельных производственных затрат, показывающая зависимость их уровня от размера производства в пункте t.
Критерий оптимальности запишется
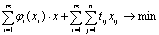 (4.40)
(4.40)
![]() (4.41),
(4.41),
а условия будут выглядеть
![]()
(i = 1, 2, …, m; k = 1,2.....Кi) (4.42)
xij ³ 0 (i = 1, 2, …, m; j = 1, 2, …, n) (4.43)
xi ³ 0 (i = 1, 2, …, m). (4.44)
Здесь условия (4.42) отражают тот факт, что размер предприятия может быть равен тому или иному из возможных типовых проектов.
Аналогично проделанному ранее, воспользовавшись условием (4.42), перепишем критерий оптимальности
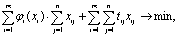 (4.45)
(4.45)
преобразовав
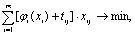 (4.46)
(4.46)
получим критерий оптимальности нелинейной транспортной задачи.
Введение в модель задачи развития и размещения нелинейности и дискретности (целочисленности) существенным образом затрудняет решение. Точные методы решения подобных задач, как правило, сложны и не универсальны. Рассмотрим процесс решения таких задач на примере приближенного метода «коэффициентов интенсивности», хорошо интерпретируемого экономически.
Метод «коэффициентов интенсивности» основан на замене однократного решения нелинейной задачи развития и размещения с дискретными переменными многократным решением серии обычных линейных транспортных задач с непрерывными переменными. Переход от одной транспортной задачи к другой осуществляется взаимосвязанным изменением мощности и соответствующих ей удельных производственных затрат для какого-либо одного пункта производства.
Другое с.106 МЭП Грачёв§3. Оптимизация производственного процесса
Любой производственный процесс формально математически можно описать парой векторов (х, у), где х – вектор затрат и у – вектор выпусков. Например, если в процессе производства затрачиваются продукты п типов и выпускаются продукты m типов, то x = (– x1, …, – xn), где xi – количество затрачиваемого продукта (ресурса) i-го типа, a yj – количество выпускаемого продукта j-го типа (i = 1…n; j = 1…m). Пара (х, у) называется вектором затрат-выпусков и формально отражает экономическое содержание производственного процесса. Как правило, имеющаяся производственная технология позволяет реализовать не один, а множество производственных процессов, каждому из которых соответствует свой вектор затрат-выпусков. Множество всех таких векторов затрат-выпусков называется производственным множеством (или технологическим множеством). С экономической точки зрения изучение производства может быть представлено как изучение структуры производственного множества. Попробуем подойти к рассмотрению структуры производственного множества с позиций многокритериальной оптимизации.
Итак, пусть производственное множество Т представляет собой некоторое множество векторов в пространстве Rn+m. Что означает в данном случае доминирование по Парето? Возьмем два производственных процесса
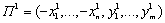 ,
,
 .
.
(компоненты вектора затрат берут со знаком минус). Условие 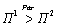 сводится к тому, что
сводится к тому, что ![]() и
и ![]() для всех i = 1…n и j = 1…m (хотя бы одно неравенство должно быть строгим). Таким образом, производственный процесс П1 доминирует по Парето производственный процесс П2 тогда и только тогда, когда для производственного процесса П1 затраты продуктов (ресурсов) каждого типа не превосходят затрат при производственном процессе П2, а выпуск продукта каждого типа при производственном процессе П1 не меньше, чем при П2. Поэтому в случае
для всех i = 1…n и j = 1…m (хотя бы одно неравенство должно быть строгим). Таким образом, производственный процесс П1 доминирует по Парето производственный процесс П2 тогда и только тогда, когда для производственного процесса П1 затраты продуктов (ресурсов) каждого типа не превосходят затрат при производственном процессе П2, а выпуск продукта каждого типа при производственном процессе П1 не меньше, чем при П2. Поэтому в случае ![]() всякий разумный экономист, безусловно, выберет П1, а не П2. Это дает основание в качестве оптимальные – с экономической точки зрения – производственных процессов рассматривать Парето-оптимальные векторы множества Т. Для характеризации Парето-оптимальных векторов воспользуемся следующими правилами:
всякий разумный экономист, безусловно, выберет П1, а не П2. Это дает основание в качестве оптимальные – с экономической точки зрения – производственных процессов рассматривать Парето-оптимальные векторы множества Т. Для характеризации Парето-оптимальных векторов воспользуемся следующими правилами:
Правило 1. Пусть Q Í Y – произвольное множество векторных оценок. Если векторная оценка у* = (у1*,...,ym*) доставляет максимум функции ![]() , где все aj > 0, mo векторная оценка у* является Парето-оптимальной во множестве Q.
, где все aj > 0, mo векторная оценка у* является Парето-оптимальной во множестве Q.
Правило 2. Пусть Q Í Y – выпуклое множество, у* Î Q – Парето-оптимальная векторная оценка на множестве Q. Тогда найдутся такие неотрицательные числа aj ³ 0, j = 1...m, что функция 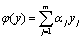 достигает максимума на множестве Q в точке у*.
достигает максимума на множестве Q в точке у*.
Правила 1 и 2 указывают «способ перебора» Парето оптимальных точек заданного множества Q: зафиксировав положительный «вектор весов» a = (a1,..., aт) и найдя максимум взвешенной суммы ![]() получаем некоторую точку Парето-оптимального множества.
получаем некоторую точку Парето-оптимального множества.
Пусть a = (a1, …, an), b = (b1, …, bm) – векторы с положительными компонентами. В силу правила 1, получаем:
А) Всякий вектор затрат-выпусков 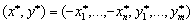 , который доставляет на множестве Т максимум функции
, который доставляет на множестве Т максимум функции
j(a, b)(x, y) = (a, x) + (b, y) = (b1 y1 + … + bm ym) – (a1 x1 + … + an xn),
является Парето-оптимальным.
В случае, когда множество Т является выпуклым (с содержательной точки зрения это означает возможность «дробления» затрачиваемых и произведенных продуктов), справедливо и обратное утверждение.
Б) Если производственный процесс 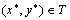 оптимален в Т по Парето, то найдутся такие векторы a и b с неотрицательными компонентами, что
оптимален в Т по Парето, то найдутся такие векторы a и b с неотрицательными компонентами, что ![]() доставляет максимум функции j(a, b) на множестве Т.
доставляет максимум функции j(a, b) на множестве Т.
Экономическая интерпретация этих утверждений такова. Векторы a и b можно рассматривать как гипотетические (назначенные произвольно) векторы цен на затрачиваемые и на выпускаемые продукты (ai – цена единицы затрачиваемого продукта i-го типа, bj – цена единицы выпускаемого продукта j-гo типа). Тогда j(a, b)(x, y) – прибыль от реализации производственного процесса (x, у) по ценам (a, b). Утверждение А) имеет при этом следующий экономический смысл: всякий производственный процесс, который максимизирует прибыль при некоторых гипотетических ценах, является Парето-оптимальным.
Утверждение Б) означает, что всякий Парето-оптимальный производственный процесс будет максимизировать прибыль при некоторых гипотетических векторах цен a и b (в этом случае некоторые компоненты этих векторов могут быть равны нулю).
Полные и дополнительные затраты
Как мы показали, транспортно-производственная модель (4.63)-(4.70) была получена некоторой детализацией более простой производственной модели (4.58)-(4.62). Однако не всегда применение более сложных и детальных моделей оправданно и дает лучшие результаты решения. Так, например, в отрасли, где влияние транспортного фактора на процессы развития и размещения производства незначительно, применение транспортно-производственных моделей лишь затруднит и осложнит проведение оптимизационных расчетов без какого-либо выигрыша в эффективности результата решения.
Приведем простой условный пример. Пусть в нашей задаче развития и размещения участвует один потребитель и две возможные точки нового строительства (поставщики). Ближайшая от потребителя точка расположена от него в 10 км, а удаленная — в 50 км. Следует выбрать для строительства предприятия-поставщика одну из них. Доля транспортных затрат в сумме транспортных и производственных составляет более 90%. Поэтому кажется очевидным преимущество ближайшего варианта, а производственные затраты можно не учитывать. Так ли это? Погрузочно-разгрузочные затраты равны 10 р./т, движенческие - 0,01 р./км, удельные производственные равны 1 р./т для ближайшей точки нового строительства и 0,5 р./т — для дальней. Такое различие может объясняться местными условиями. Посчитаем уровень транспортно-производственных затрат для того и другого варианта строительства предприятия. Сумма удельных затрат на производство и перевозку (последние, в свою очередь, складываются из затрат на погрузку-разгрузку и передвижение) по вариантам составит для ближайшего поставщика — 1,0 р./т + 10 р./т + 0,01 р./т-км * 10км = I 1,1 р./т;
для удаленного − 0,5 р./т + 10 р./т + 0,01 р./т-км * 50 км = 11,0 р./т.
Оказывается, несмотря на незначительный удельный вес производственных затрат (9% в первом варианте и 4,6% − во втором), более дешевым является вариант строительства в удаленной точке, где затраты на производство ниже. Дело в том, что подавляющий удельный вес транспортных расходов создается преимущественно погрузочно-разгрузочными затратами, не зависящими от расстояния перевозки. Их величина (10 р./т) хотя и велика, но постоянна в обоих вариантах, и, следовательно, может (и должна) быть отброшена.
Эти два варианта одинаковы по результату − строим один и тот же завод, одной и той же мощности (равной спросу потребителя), но только в той или другой точке. Соответственно разным точкам строительства варианты отличаются по затратам. Ясно, что при одинаковом результате лучшим будет более дешевый вариант (с минимумом затрат). При сравнении вариантов нас интересуют не общие величины затрат, а разница между этими величинами − насколько один вариант дороже (дешевле) другого. Л разница зависит лишь от меняющихся частей затрат и не зависит от постоянных (одинаковых для всех вариантов) частей. Действительно, учтем лишь зависящие от нашего решения (выбора того или иного варианта) затраты. Получим для ближайшего поставщика − 1,0 р./т + 0,1 р./т = 1,1 р./т; для удаленного − 0,5 р./т + 0,5 р./т = 1,0 р./т.
Как видим, опять выгоднее второй вариант. Причем, он дешевле первого все на ту же величину − 0,1 р./т. Следовательно, хотя в данной отрасли удельный вес производственных затрат крайне низок (менее 10%), модель и задача развития и размещения производства должны быть транспортно-производственными.
Таким образом, влияние транспортного и (или) производственного фактора зависит не от доли затрат на эти факторы в общей сумме затрат, а от соотношения меняющихся частей транспортных и (или) производственных затрат. Другими словами, необходимо рассматривать соотношение затрат, которые колеблются по вариантам, зависят от результатов нашего решения, отбросив ту часть затрат, которая постоянна и не зависит от решения. Зависящие от результатов решения затраты называются также дополнительными, так как они возникают в результате выбора нами того или другого варианта «дополнительно» к постоянным затратам, безразличным к нашему решению.
Сумма дополнительных и постоянных затрат называется полными.
Более того, постоянную часть затрат следует исключать из рассмотрения не только на стадии постановки, при выборе типа модели, метода решения задачи и т. п., но и при проведении расчетов (как мы только что проделали). Это не только упростит вычисления, но и позволит избежать возможных ошибок.
Покажем это, рассмотрев еще один пример.
Прошлые и будущие затраты
Имеется два варианта строительства ГЭС. Первый предполагает ее возведение в наиболее благоприятном створе реки. Стоимость строительства составит 1 млрд. р. Однако образующееся в этом случае водохранилище затопит участок железной дороги стоимостью в 0,1 млрд. р. Затраты на строительство обходного участка пути в этом случае составят 0,15 млрд. р. Во избежание затопления предложен второй вариант строительства ГЭС ниже по течению реки. Ввиду менее благоприятных условий стоимость ГЭС в этом случае составит 1,2 млрд. р. Казалось бы, выбор второго варианта, как более дешевого, очевиден (см, табл. 4.17).
Таблица 4.17
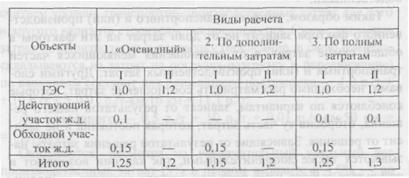
Попытаемся поискать постоянную часть затрат, не зависящую от результатов нашего решения. Ею является стоимость действующего участка железной дороги, затапливаемого по первому варианту. Действительно, затапливаем ли мы этот участок по варианту I, не затапливаем ли по варианту II, не строим ГЭС вообще — во всех этих случаях его стоимость постоянна, равна 0,1 млрд. р. и не зависит от нашего решения. Эта сумма уже истрачена ранее на строительство участка, и мы не можем изменить ее.
Тогда отбросим постоянные (прошлые в данном случае) затраты и проведем расчет лишь по дополнительным (будущим) затратам. Теперь уже более дешевым является первый вариант. Ведь будущие затраты сложатся из 1,0 млрд. р. на ГЭС и 0,15 млрд. р. на обходной участок «пути». Всего же «выложить из кармана» потребуется 1,15 млрд. р. против 1,2 млрд. р. по второму варианту.
В чем же причина расхождений планов строительства при первом «очевидном» расчете и расчете по дополнительным затратам? «Очевидный» расчет некорректен. Ведь затраты в 1,25 млрд. р. для варианта I относятся к результату ГЭС плюс участок железной дороги, а затраты в 1,2 млрд. руб. для вари анта II соответствуют результату лишь одной ГЭС. Дешевый вариант будет лучшим, если для всех вариантов результат одинаков (либо ГЭС, либо ГЭС + ж. д.). Если привести второй вариант к одинаковому результату с первым, то для второго варианта следует добавить затраты на участок железной дороги в 0,1 млрд. р. Тогда будем иметь третий расчет — расчет по полным затратам. Он соответствует длительному отрезку времени, охватывает как прошлые затраты, так и будущие. В нем по первому варианту относительная дешевизна ГЭС (1,0 млрд. р.) связана с удорожанием затрат на участок железной дороги (его «двукратное» строительство — 0,1 млрд. р. и затем еще 0,15 млрд. р.). Второй же вариант связан с удорожанием ГЭС (1,2 млрд. р.), но зато участок пути «строим» однократно (0.1 млрд. р.). Таким образом, как по дополнительным, так и по полным затратам (как во втором, так и в третьем расчетах) вариант I выгоднее, дешевле. Причем дешевле на одну и ту же сумму (0,15 млрд. р.), что дополнительно подтверждает правильность этих расчетов.
Отметим, что при расчете только по дополнительным затратам оба варианта также приведены к одинаковому результату. В этом случае результатом является одна ГЭС. Добавление же к затратам по варианту I затрат на строительство обходного участка пути (0,15 млрд р.) выступает как своеобразный штраф за нанесенный ущерб, как нагрузка к более выгодному месторасположению ГЭС.
Как видим из этого небольшого примера, правильный расчет по полным затратам не только требует большой вычислительной работы, но и затруднителен вследствие неочевидности. Есть реальная опасность провести его некорректно (см. «очевидный» расчет в табл. 4.17). Поэтому при оптимизационных расчетах следует учитывать лишь дополнительные затраты, т. е. ту часть полных затрат, которая зависит (меняется) от нашего решения. В частности, прошлые затраты как постоянные от нашего решения не зависят и учитываться не должны. В дополнительные затраты войдут только будущие, предстоящие затраты (целиком или же лишь частично, как мы это видели в первом примере).
Производственные затраты, зависящие от мощности
Рассмотрим в этой связи возможные виды зависимости удельных производственных затрат q(x) от общей мощности предприятия х.
Использование линейной зависимости
![]() (4.71)
(4.71)
где а и b — некоторые коэффициенты, дает слишком грубое и неточное приближение к действительности, поскольку предполагает равномерное снижение производственных затрат на единицу продукции при любом увеличении мощности. Кроме того, при некоторых достаточно больших значениях мощности х значения удельных затрат q(x) становятся нулевыми, что попросту нереально.
Практически наблюдается тенденция постепенного замедления снижения затрат на единицу готового продукта при росте мощности предприятия. Наиболее часто при выборе формы зависимости удельных затрат от мощности предприятия останавливаются на гиперболической функции
![]() (4.72)
(4.72)
как наиболее явно и в наиболее простой форме отражающей эту зависимость. Гипербола имеет прозрачную экономическую интерпретацию. Коэффициент а отражает условно переменные удельные расходы. Общий объем условно переменных расходов прямо пропорционален выпуску и определяется произведением постоянного удельного норматива а (например, нормы расходов сырья на единицу продукции) на объем выпуска х. Коэффициент b отражает общие условно постоянные расходы. В расчете на единицу продукции условно постоянные расходы тем меньше, чем больше объем выпуска х. Однако, строго говоря, неизменность обшей величины условно постоянных расходов есть частный случай, встречающийся при известных условиях и в определенных пределах изменения мощности. Не случайно они названы не просто постоянными, а условно постоянными.
Более точным является деление издержек на возрастающие строго пропорционально мощности и возрастающие более медленно. Математически это выразит функция удельных затрат
![]() (4.73)
(4.73)
частным случаем которой при п = 1 будет гипербола. Умножением над: получаем функцию f(х), функцию общих затрат на весь выпуск
![]() (4.74)
(4.74)
Однако тенденция снижения удельных производственных затрат при росте мощности не абсолютны. В тех случаях, когда эта тенденция носит ограниченный характер, применимы другие формы зависимости.
Для параболы
q(x) = а - bх + сх2 (4.75)
характерно, что изменение функции удельных производственных затрат q(x) под влиянием размеров производствах происходит не с постоянным, как для линейной зависимости (4.71), темпом b. Перепишем выражение (4.75) несколько по-иному
q(x) = а - (b - сх)х. (4.76)
Темп изменения удельных производственных затрат в случае параболы есть функция от х и равен b - сх.
Причем это изменение (уменьшение) не ограничено, как в случаях (4.72) и (4.73) асимптотой. Темп замедления, все более
уменьшаясь с ростом х, минует нулевое значение. При дальнейшем росте x это уменьшение будет идти по области отрицательных чисел. Иными словами, при определенном значении х уменьшение превращается в свою противоположность, став отрицательным уменьшением, т. е. увеличением. Таким образом, параболическая зависимость удельных производственных затрат от размеров производства соответствует случаю, когда при увеличении мощности сверх некоторых пределов наблюдается увеличение удельных производственных затрат.
В ряде случаев зависимость удельных производственных затрат от мощности адекватно описывается кривой третьего порядка
![]() (4.77)
(4.77)
Производственные затраты, зависящие от специализации
Производственные затраты, зависящие от специализации (т. е. от выпуска каждого данного k-го вида продукции), в отличие от затрат, зависящих от концентрации (т. е. от общего выпуска), в гораздо большем числе случаев линейны. Их общая величина определяется прямым счетом, умножением затрат h. на объемы выпуска данного k-го вида продукции на i-м предприятии xik Нормы затрат hk в этом случае постоянны, разнятся лишь в зависимости от вида продукта и не зависят от размеров его производства и пункта производства.
Общая сумма производственных затрат, зависящих от специализации, по всей задаче развития и размещения сложится из всех таких произведений для разных видов продукции и разных пунктов производства
![]() (4.78)
(4.78)
Преобразуем далее выражение (4.78). Учтем, что в наших моделях суммарный вывоз k-й продукции из каждого i-го пункта
производства во все пункты потребления j (величина хijk) равен объему производства xik
![]() (4.79)
(4.79)
В свою очередь, преобразуем далее выражение (4.79). Учтем, что суммарный ввоз k-й продукции в j-й пункт потребления из всех пунктов производства i равен потребности данного потребителя
![]() (4.80)
(4.80)
В итоге получили выражение (4.80), из которого следует, что общая сумма производственных затрат, зависящих от специализации, для всей задачи развития и размещения производства является величиной постоянной. Постоянной — при любых значениях неизвестных хik и хijk, т. е. не зависит от нашего решения (а следовательно, и не влияет на него). Таким образом, эти затраты можно (и следует) не учитывать при решении задачи.
Формально доказательство неизменности общей суммы этих затрат основывается на ряде последовательных выкладок, возможных благодаря неизменности нормативов k от пункта производства i. Экономически это соответствует случаю единства технологии во всех пунктах производства, на всей территории, охватываемой оптимизационным расчетом. Необходимо также и требование единства условий применения этой технологии в различных пунктах производства.
В случае же различий в величине удельных производственных затрат, зависящих от специализации, в различных пунктах производства i мы имеем уже нормативы hik. Формально это не позволит вынести величину hik за знак суммы по i в выражении (4.78), что сделает невозможным и все дальнейшие выкладки.
Тема 7. Модели управления производственными запасами с учётом спроса и цен на продукцию
Лекции 14.
§1. Основная модель
Определим функцию изменения запаса, т. е. связь между количеством единиц товара на складе (обозначим его через Q) и временем t. Будем считать, что имеется один вид товара.
Если на товар имеется спрос, то функция изменения запаса Q = Q(t) убывает. Если товар, наоборот, завозят на склад, то эта функция возрастает.
Затраты, связанные с запасами, можно разделить на три части.
· Стоимость товара.
· Организационные издержки. Это расходы, связанные с оформлением товара, его доставкой, разгрузкой и т. д.
· Издержки на хранение товара. Это затраты на аренду склада, амортизацию в процессе хранения и т. д.
Рассмотрим основные величины и предположения, принятые в рамках основной модели.
1. Цена единицы товара – с у. е. Цена постоянна, рассматривается один вид товара.
2. Интенсивность спроса – d единиц товара в год. Будем считать, что спрос постоянный и непрерывный.
3. Организационные издержки – s у. е. за одну партию товара. Будем считать, что организационные издержки не зависят от размера поставки, т. е. от количества единиц товара в одной партии.
4. Издержки на хранение запаса – h у. е. на единицу товара в год. Будем считать эти издержки постоянными.
5. Размер одной партии товара постоянен – q единиц. Партия поступает мгновенно в тот момент, когда возникает дефицит, т. е. когда запас на складе становится равным нулю.
При сделанных предположениях график функции изменения запаса будет таким, как показано на рис. 1: он состоит из повторяющихся циклов пополнения запаса между двумя соседними дефицитами. Вертикальные отрезки отвечают мгновенному пополнению запаса.
Параметры с, d, s, h считаются заданными. Задача управления запасами состоит в выборе параметра q таким образом, чтобы минимизировать годовые затраты.
Для решения сформулированной задачи надо прежде всего выразить эти затраты через параметры с, d, s, h, q.
1. Поскольку годовая интенсивность спроса равна d, а цена единицы товара – с, то общая стоимость товара в год равна cd.
2. Поскольку в одной партии q единиц товара, а годовой спрос равен d, то число поставок равно d/q. В течение года организационные издержки равны
![]() .
.
3. Средний уровень запаса равен отношению площади под графиком за цикл к продолжительности цикла. Этот средний уровень равен q/2 (на рис. 1 обозначен пунктиром). Поскольку годовые издержки на хранение единицы товара равны h, то общие издержки на хранение составляют
![]() .
.
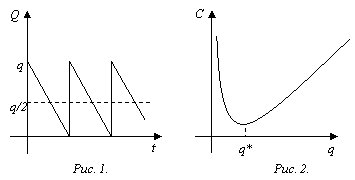

Таким образом, общие издержки С вычисляются по формуле
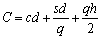 .
.
Требуется найти такое число q*, чтобы функция С = C(q) принимала наименьшее значение на множестве q > 0 именно в точке q*.
График функции С = C(q) показан на рис. 2.
Для нахождения точки q* минимума функции С = C(q) найдем ее производную (с, d, s, h – фиксированные числа):
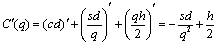 .
.
Приравнивая C'(q) к нулю, получаем
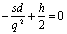 .
.
Отсюда можно найти q*. Имеем:
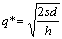 .
.
Полученная формула называется формулой оптимального запаса или формулой Харриса (Harris).
§2. Модель производственных поставок
В основной модели предполагалось, что поступление товаров на склад происходит мгновенно. Это предположение достаточно хорошо отражает ситуацию, когда товар поставляется в течение одного дня (или ночи). Если товары поставляются с работающей производственной линии, необходимо модифицировать основную модель. В этом случае к параметрам с, d, s и h добавляется еще один — производительность производственной линии р (единиц товара в год). Будем считать ее заданной и постоянной.
Эта новая модель называется моделью производственных поставок. В начале каждого цикла происходит "подключение" к производственной линии, которое продолжается до накопления q единиц товара. После этого пополнения запасов не происходит до тех пор, пока не возник дефицит.
График функции изменения запаса имеет вид, изображенный на рис. 3.
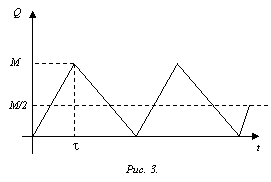

Общие издержки C(q), как и в основной модели, состоят из трех частей.
1. Общая стоимость товара в год равна cd.
2. Годовые организационные издержки равны ![]() .
.
3. Издержки на хранение вычисляются следующим образом. Пусть t – время поставки (рис. 3). В течение этого времени происходит как пополнение (с интенсивностью р), так и расходование (с интенсивностью d) запаса. Увеличение запаса происходит со скоростью p – d. Поэтому достигнутый к концу периода пополнения запаса максимальный его уровень М вычисляется по формуле
М = (p – d) t
(заметим, что М < q). Однако,
pt = q
(за время t при интенсивности производства р произведено q единиц товара). Из последних двух равенств следует, что
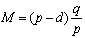 .
.
Средний уровень запаса, как и в основной модели, равен половине максимального, т. е. М/2. Таким образом, издержки на хранение запаса равны ![]() .
.
Общие издержки вычисляются по формуле
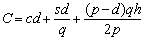 .
.
Оптимальный размер поставок q получаем из уравнения
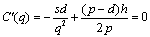 .
.
Имеем: 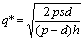 .
.
Замечание. Найдя оптимальный размер заказа, можно определить оптимальное число поставок за год п* и соответствующие продолжительность поставки t* и продолжительность цикла пополнения запаса t*.
§3. Модель поставок со скидкой
Рассмотрим ситуацию, описываемую в целом основной моделью, но с одной особенностью, которая состоит в том, что товар можно поставлять по льготной цене (со скидкой), если размер партии достаточно велик. Иными словами, если размер партии q не менее заданного числа q0, товар поставляется по цене с0, где с0 < с.
Функция общих издержек C(q) задается в таком случае следующим образом: 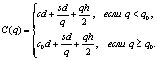 Нетрудно видеть, что функция С(q) в точке q = q0 разрывна. Обе функции
Нетрудно видеть, что функция С(q) в точке q = q0 разрывна. Обе функции 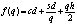 и
и 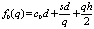 имеют минимум в точке, где f¢ (q) = f0¢ (q) = 0, т. е. в точке
имеют минимум в точке, где f¢ (q) = f0¢ (q) = 0, т. е. в точке ![]() . Для выяснения вопроса о том, какой размер партии оптимален, следует сравнить значения функции C(q) в точках
. Для выяснения вопроса о том, какой размер партии оптимален, следует сравнить значения функции C(q) в точках ![]() и q0, и та точка, где функция C(q) принимает меньшее значение, будет оптимальным размером партии q* в модели поставок со скидкой (см. рис. 4, 5).
и q0, и та точка, где функция C(q) принимает меньшее значение, будет оптимальным размером партии q* в модели поставок со скидкой (см. рис. 4, 5).
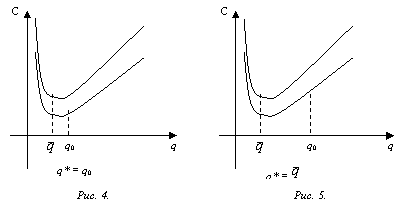

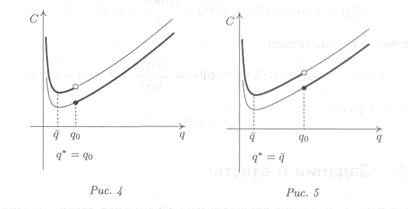
Замечание. Может случиться так, что C(![]() ) = C(q0). Тогда в качестве q* можно взять любое из чисел
) = C(q0). Тогда в качестве q* можно взять любое из чисел ![]() и q0.
и q0.
§4. Моделирование инвестиций и анализ их эффективности
Понятие инвестиции. Основные виды инвестиции
Инвестиции представляют сложный комплекс экономических явлений, разворачивающихся в течение одного или ряда периодов времени и предусматривающих первоначальные вложения (трату) денежных средств в приобретение активов (инвестиционных благ) с целью получения от них планируемых доходов в будущих периодах.
Примеры инвестиций:
Приобретение объекта недвижимости, например квартиры с целью ее более выгодной продажи через определенное время, Приобретение лицензии на производство изделий. Покупка оборудования для пекарни. Приобретение самолетов для открытия новой авиалинии авиакомпанией.Существуют различные подходы к классификации видов инвестиций
1. По типам инвестиционных объектов.
Здесь различают инвестиции в финансовые активы и инвестиции в реальные активы.
К финансовым активам относят: депозитные банковские вклады, ценные бумаги (облигации, акции), доли в фондах недвижимости и др.
К реальным активам относят: материальные средства производства (машины и оборудования, здания, транспортные средства, оргтехника, участки земли и др.), а также нематериальные активы, такие как лицензии и патенты, торговые марки предприятия и ноу-хау.
2. По областям применения инвестиционных объектов.
Различают инвестиции в создание нового предприятия (или филиала существующего), дополняющие и текущие инвестиции, к дополняющим инвестициям относят: инвестиции в расширение производства (в увеличение производственной мощности); в исследования и разработки; инвестиции в рационализацию производства; в обеспечение стабильности производства.
Инвестиции в расширение производства имеют целью увеличение производственной мощности предприятия. Инвестиции в рационализацию производства ориентированы на снижение издержек, например посредством роботизации. Инвестиции в обеспечение стабильности производства имеют целью предотвращение негативных явлений, могущих привести к кризисной ситуации на предприятии. К ним относятся: создание страховых запасов сырья и комплектующих, приобретение пакетов акций предприятий поставщиков, рекламные мероприятия, регулярные циклы повышения квалификации персонала.
Важным классификационным признаком инвестиций является степень зависимости их от других элементов системы «предприятие». Так, решение о реализации инвестиций влияет на финансовые решения, на планы сбыта, закупок материалов, обучения персонала и др.
Инвестиционный процесс и принятие инвестиционных решений инвесторами/предприятием
Процесс управления инвестиционной деятельностью является существенным компонентом общего управленческого процесса на предприятии, поскольку:
Инвестиционные решения в большинстве случаев являются долгосрочно действующими и характеризуются связанностью капитала. Инвестиционные решения являются ограниченно или вообще не корректируемыми. Для своей реализации инвестиции требуют затрат значительных финансовых средств и других дефицитных ресурсов.В соответствии с общей схемой управленческого процесса на предприятии качестве основных этапов инвестиционного процесса выделяют фазы планирования, реализации и эксплуатации инвестиций.
Этап планирования охватывает фазы инициирования принятия решения и собственно принятия решения.
Фаза инициирования принятия решения включает: наблюдение, усвоение проблемы, формирование целей инвестирования, а также формирование списка возможных мероприятий.
При применении распространенной схемы планирования «снизу вверх» последняя фаза в значительной степени реализуется в различных подразделения предприятия.
Так, руководство цеха может быть озабочено тем, что такое-то оборудование производит все больше бракованных деталей, и выступает с предложением о его замене. Директор коммерческой службы, выяснив, что конкуренты внедрили новое, более современное оборудование, что позволило им установить цены ниже существующих, предлагает произвести замену оборудования с модернизацией.
Служба сбыта выявила новый, перспективный рынок сбыта и предлагает проект расширения производства.
В большинстве случаев у предприятия существуют не только наборы инвестиционных предложении, но ряд альтернативных вариантов их финансирования. Кроме того, если межлу инвестиционными предложениями есть зависимость, то необходимо рассматривать варианты (альтернативы), представляющие совокупности всех взаимосвязанных предложений,
В процессе подготовки инвестиционного решения предприятие определяет, какие варианты финансирования, в частности финансовые активы, следует создать для привлечения денежных средств. Соответствующие комбинации программ инвестирования - финансирования определяют альтернативы предприятия.
Собственно к фазе принятия решения относятся этапы:
- анализа инвестиционных альтернатив с выявлением их допустимости по ограничениям финансового характера, а также возможностей материально - технического обеспечения; оценки выявленных альтернатив на соответствие их целям предприятия, финансовому плану, данным, полученным на основе макроэкономических прогнозов; этап собственно выбора лучшей инвестиционной альтернативы. Этап реализации предусматривает проведение более детального планирования связанных с выбранным решением платежей, а также собственно процесс осуществления проекта, включая приобретение оборудования, его монтаж, обучение персонала и т. д.
Основным методом оценки и выбора инвестиционных альтернатив является применение модельного подхода.
Под инвестиционной моделью (моделью инвестиционного планирования) понимается математическая модель, предназначенная для оценки эффективности инвестиций по отношению к определенной заданной цели или системе целей.
Оценочным критерием инвестирования в модели выступает экономический принцип: на основе предстоящих и текущих платежей должна образовываться долговременная прибыль предприятия в виде прироста капитала, увеличения потока поступлений, увеличения рентабельности.
Структура модели варьируется в зависимости от отраслевой принадлежности инвестиций и целей, для достижения которых они осуществляются.
Возможные альтернативы описываются условиями, включая:
- условия инвестирования, охватывающие взаимосвязи между инвестиционными альтернативами и такими разделами плана предприятия, как план сбыта, финансовый план, план закупок и др.; производственные условия.
Выбор решения осуществляется из альтернатив с наивысшей оценкой.
Основная модель инвестиционного планирования (модель И. Фишера)
Если инвестор – физическое лицо, то согласно анализу И. Фишера его цели инвестирования являются производными от психофизических потребностей, которые удовлетворяются посредством реальных благ. К последним относятся: долгосрочные (жилье), краткосрочные (средства пропитания) и услуги. В свою очередь, реальные блага в условиях рыночных отношений приобретаются благодаря денежным доходам, основной частью которых является заработная плата, сбережения, полученные кредиты и доходы от инвестиций более ранних периодов.
Для инвестора – юридического лица цели инвестирования формулируются менеджерами /директором и являются производными от целей предприятия.
Оценочным критерием инвестирования выступает экономический принцип: на основе денежных доходов (сальдо поступлений и выплат) от инвестирования должны обеспечиваться прирост капитала предприятия, рентабельность, увеличение потока отчислений на выплату дивидендов и обеспечение социальных целей предприятия.
В зависимости от ряда факторов потоки будущих денежных доходов для разных вариантов инвестиционного плана различаются в трех главных аспектах:
• по величине потока за период (д. е. /период);
• по степени неопределенности получения ожидаемого дохода в отдельном периоде;
• по временной структуре денежного потока доходов (повышательная тенденция, снижение потока доходов).
Рассмотрим основные подходы к моделированию предпочтений инвесторов относительно вариантов инвестиционного плана.
В соответствии с объявленными целями инвестор – физическое/юридическое лицо использует одну часть своих денежных средств для инвестирования, а другую – для текущего потребления/дивидендных и социальных выплат. Для простоты ограничимся случаем, когда плановый горизонт инвестирования охватывает один временной отрезок между моментами t1 и t2
Тогда предпочтения инвестора можно охарактеризовать посредством задания семейства следующих кривых (кривых безразличия). Каждая кривая состоит из точек плоскости (с1, с2), представляющих варианты инвестиционного плана: с, – часть средств, направляемых на потребление в момент t1; с2 – денежный доход, полученный инвестором от инвестиций к моменту t2. Предполагается, что имеющаяся сумма доступных на момент t1 средств фиксирована и непотребленные средства инвестируются оптимальным образом. Все точки, лежащие на одной кривой безразличия, рассматриваются как равноценные.
Точка М на рис. 1 характеризует размер средств |ОА| инвестора, направляемых на текущее потребление (выплаты) в момент t1, и дохода |ОВ|, полученного от инвестиций в момент t2. Решение направить сумму |ОА| на текущее потребление обусловлено выбором политики дивидендных выплат и социальными целями предприятия.
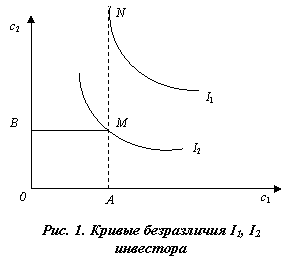

Состав дивидендно-социального портфеля текущих выплат предприятия есть функция состояния среды (конъюнктуры), требований рынка к доходности инвестированного капитала, социального положения работников предприятия и имеющихся у него на момент t1 денежных средств. В дальнейшем мы будем обозначать точки на плоскости (с1, с2) символами х, у, z. Возможность отображения предпочтений инвестора посредством кривых безразличия основывается на следующих предпосылках:
1. Сопоставимость. Инвестор в состоянии упорядочить альтернативные варианты распределения средств по предпочтению, т. е. определить для любых двух вариантов распределения х, у, что либо х более предпочтителен, чем у (пишут: ![]() ), либо у лучше чем х (
), либо у лучше чем х (![]() ), либо х равноценен у (x ~ y). Следует учесть, что соотношения типа х
), либо х равноценен у (x ~ y). Следует учесть, что соотношения типа х ![]() не указывают, в какой мере х лучше чем у, т. е. представляют лишь квазипорядок.
не указывают, в какой мере х лучше чем у, т. е. представляют лишь квазипорядок.
2. Транзитивность. Если ![]() и
и ![]() , то
, то ![]() .
.
3. Непрерывность. Если для трех вариантов х, у, z распределения средств имеет место соотношение 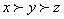 ,то существует такое aÎ (0,1), что комбинация распределений a ´ x + (1 – a) ´ z равноценна у.
,то существует такое aÎ (0,1), что комбинация распределений a ´ x + (1 – a) ´ z равноценна у.
Здесь предполагается, что всегда имеется возможность создать распределение, в котором х «участвует» с долей a, а z – с долей (1 – z). Указанная выше комбинация обозначается символом [х, z: a].
4. Ранжирование. Пусть для альтернатив х, у, ![]() ,
, ![]() , удовлетворяющих условиям
, удовлетворяющих условиям ![]() ,
, ![]() и имеет место x ~ [
и имеет место x ~ [![]() ,
,![]() : a], y~ [
: a], y~ [![]() ,
,![]() : b].Тогда, из того что a > b, следует, что
: b].Тогда, из того что a > b, следует, что ![]()
Если выполнены перечисленные предпосылки, то можно построить функцию полезности U(x), обладающую свойствами:
![]() тогда и только тогда, если U(x) > U(y),
тогда и только тогда, если U(x) > U(y),
х ~ у тогда и только тогда, если U(x) = U(y).
В качестве наиболее характерных свойств функции U(x) отметим:
1. Функция U(x) = U(c1 c2) возрастает, если увеличивается хоть одна из компонент вектора х.
2. Предельная полезность каждой дополнительной единицы с1 (c2) убывает.
К наиболее часто встречающимся функциям полезности можно отнести функцию Кобба-Дугласа: ![]() ,
,
где А, a – константы, 0 < a <1.
Так, два инвестора, имеющие различные временные предпочтения относительно текущего и будущего потребления, и обладающие совместным капиталом, будут отстаивать различные варианты инвестиционных программ: И. Фишером было установлено, что конфликты такого рода не возникают при наличии совершенного рынка капиталов, для которого выполняются следующие предпосылки:
1. Любой инвестор обладает возможностью как получить кредит, так и вложить капитал по единой процентной ставке.
2. Рынок капитала информационно доступен и прозрачен. Поэтому инвесторы и предприятия исходят при формировании своих планов потребления и проектов инвестиций из одной и той же информации (однородность ожиданий инвесторов).
3. Транзакциоицые издержки и налоги не учитываются.
Методика инвестиционного планирования предусматривает составление полной программы инвестирования и финансирования, в которой при оценке вариантов полностью учитывается влияние инвестиций на параметры финансового плана предприятия. Обычно эти оценки осуществляются при проведении системного анализа планов, что связано с большими затратами.
Если же на предприятии некоторое подразделение самостоятельно принимает решение относительно инвестиционного проекта, то у него имеется мало средств для оценки влияния этого проекта на политику финансирования предприятия. Проще бывает провести упрощенный, или экспресс-анализ, в рамках которого частично учитывается влияние инвестиционного проекта на финансовую сферу предприятия.
Возможности применения экспресс-анализа базируются на том факте, что с финансированием связаны определенные обязательства (затраты) по оплате процентов и всегда возникает вопрос: будут ли эти затраты покрываться доходами от инвестиционной программы. В такой постановке последовательности платежей, связанные с инвестициями, могут исследоваться изолированно, вне связи с потоками платежей финансирования предприятия. На передний план выступают такие показатели финансирования, как процентные ставки, определяющие стоимость привлечения денежных средств.
Таким образом, при рассмотрении экономических явлений, связанных с реализацией альтернатив инвестирования, в экспресс-анализе последние отождествляются с реальными расходами и получаемыми доходами по инвестиционному проекту. В этой главе предполагается, что имеются надежные прогнозы расходов и доходов по периодам реализации каждой альтернативы.
Выбор методов обоснования инвестиционного проекта существенно зависит от того, характеризуется ли проект значительной динамикой доходов и расходов по периодам реализации или проект можно охарактеризовать среднегодовыми показателями затрат и результатов.
В первом случае используют динамические методы, а во втором — статические методы оценки проектов.
Оценка эффективности инвестиций
Эффективность инвестиций определяется сопоставлением эффекта от их осуществления с величиной вложенных средств,
Расчет экономической эффективности инвестиций должен производиться на всех стадиях инвестиционного цикла, в первую очередь на стадии прогнозирования и планирования.
Прогнозные расчеты осуществляются с целью формирования возможных альтернатив вложения капитала, определения оптимального объема и выбора форм финансирования инвестиций, составления оптимальной инвестиционной программы.
В международной практике определяются показатели:
- коммерческой (финансовой) эффективности (учитывает финансовые последствия реализации проекта для его непосредственных участников); бюджетной эффективности (отражает финансовые последствия осуществления проекта для федерального, регионального или местного бюджета); экономической эффективности (учитывает затраты и результаты, связанные с реализацией проекта).
Оценка предстоящих затрат и результатов при определении эффективности инвестиционного проекта осуществляется в пределах расчетного периода, включающего проектирование, создание и эксплуатацию объекта.
В индустриально развитых странах разработан и широко применяется большой арсенал методов оценки эффективности инвестиционных проектов, основанных преимущественно на сравнении эффективности (прибыльности) инвестиций в различные проекты. При этом в качестве альтернативы вложениям средств в рассматриваемое производство выступают финансовые вложения в другие производственные объекты, помещение финансовых средств в банк под проценты или их обращение в ценные бумаги.
При оценке эффективности инвестиций соизмерение разновременных расходов и доходов осуществляется путем приведения их к одному (базовому) моменту времени, обычно к дате начала инвестирования.
Процедура приведения разновременных платежей к базовой дате называется дисконтированием, а величина ссудного процента - нормой дисконта. При выборе ставки дисконтирования ориентируются на существующий или ожидаемый усредненный уровень ссудного процента за долгосрочный кредит.
Для оценки эффективности производственных инвестиций применяются, как правило, следующие показатели:
- чистый приведенный доход; внутренняя норма доходности; срок окупаемости инвестиций; индекс доходности.
Чистый приведенный доход ЧПД, рассчитывается по формуле
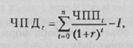
где t — годы реализации инвестиционного проекта, включая этап строительства (t = 0, 1, 2, 3, ..., п); ЧПП, — чистый поток платежей, включающий чистую прибыль и амортизацию по годам; r — ставка дисконтирования (уровень ссудного процента); I - инвестиции (если инвестиции распределены по периодам реализации проекта, то они также дисконтируются).
Промышленные и другие инвестиции имеют экономический смысл только в том случае, если годовой доход от них выше, чем процент по банковским депозитам (вкладам) или по другим активам.
Проект можно считать эффективным, если чистый приведенный доход имеет положительное значение.
Внутренняя норма доходности (ВНД) инвестиционного проекта представляет собой расчетную ставку процентов (rB), при которой чистый приведенный доход равен нулю, т. е. когда доходы по проекту равны инвестиционным затратам ![]()
ВНД проекта определяется в процессе расчета и затем сравнивается с требуемой инвестором нормой дохода на вкладываемый капитал. При ставке ссудного процента, равной внутренней норме доходности, инвестирование финансовых средств в проект дает в итоге тот же суммарный доход, что и помещение их в банк на депозитный счет, т. е. альтернативы экономически эквивалентны. Если реальная ставка ссудного процента меньше внутренней нормы доходности проекта, то инвестирование средств в него выгодно.
За рубежом расчет внутренней нормы доходности часто применяется в качестве первого шага при финансовом анализе инвестиционного проекта. Для дальнейшего анализа отбирают те инвестиционные проекты, которые имеют ВНД не ниже некоторого порогового значения (обычно 15 — 20 % годовых).
Срок окупаемости (СО) — это период, в течение которого первоначальные вложения и другие затраты, связанные с инвестиционным проектом, покрываются суммарным результатом его осуществления, СО может быть рассчитан из зависимости
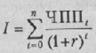
В данном случае t, обеспечивающее указанное равенство, является сроком окупаемости. Срок окупаемости можно определить приближенно по формуле
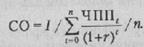
Индекс доходности (ИД) представляет собой отношение суммы приведенных эффектов к величине инвестиций:
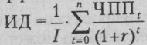
Если ИД > 1, то проект эффективен.
Наряду с перечисленными критериями может использоваться и ряд других: точка безубыточности; простая норма прибыльности; капиталоотлача и др.
Точка безубыточности соответствует объему производства, при котором балансовая прибыль производителя равна нулю, т. е. выручка от реализации совпадает с издержками производства. Данный параметр показывает, при каком минимальном объеме продаж предприятие в процессе реализации проекта будет оставаться безубыточным.
Простая норма прибыльности (ПНП) показывает, сколько чистой прибыли получено на 1 рубль/затрат или какая часть инвестиций/покрывается чистой прибылью в течение года ( ПНП = ЧП/I*100).
Капиталоотдача (КО) рассчитывается как отношение прироста продукции![]() к инвестициям
к инвестициям ![]() .
.
Коммерческая эффективность (финансовое обоснование проекта) определяется соотношением финансовых затрат и результатов, обеспечивающих требуемую норму доходности.
При определении финансовых затрат п результатов необходимо у читывать факторы внешней среды: будущий уровень инфляции, изменение спроса и цен па планируемую к выпуску продукцию, возможные изменения цен на сырье и материалы, изменения ставки ссудного процента, курса валюты, налоговых ставок и т. д.
Для инвестора проект является прибыльным, если обеспечивается требуемый уровень доходности с учетом ком не пса hi hi инфляционных потерь и риска, связанного с осуществлением проекта.
Риск характеризует возможное уменьшение реальной отдачи от капитала по сравнению с ожидаемой. Целесообразно вводить поправку к уровню процентной ставки, которая характеризует доходность по безрисковым вложениям, например по сравнению с банковским депозитом или краткосрочными ценными бумагами.
Проект считается устойчивым и эффективным, если во всех рассмотренных ситуациях интересы участников соблюдаются, а возможные неблагоприятные последствия устраняются за счет созданных запасов и резервов или возмещаются страховыми выплатами.
Тема 8. Решение задач развития и размещения производства
§1. Оптимизационные модели развития и размещения производства
Рассмотрим небольшую транспортную задачу, включающую а себя по три поставщика и потребителя (см. табл. 4.10).
Таблица 4.10
|
Мощности поставщиков |
Потребности потребителей | |||
|
реальных |
фиктивного | |||
|
4 |
4 |
4 |
4 | |
|
3 |
1 |
6 |
1 3 |
0 |
|
3 |
2 2 |
5 |
3 1 |
0 |
|
10 |
3
|
4 4 |
10 |
0 4 |
Так как суммарное наличие продукции у поставщиков составляет 16 ед., а суммарные потребности реальных потребителей - 12 ед., то задача является открытой. Для ее решения искусственно закрываем ее введением четвертого по счету, «фиктивного» потребителя.
Числа в клетках табл. 4.10 представляют собой оптимальный план перевозок продукции. Число, стоящее в клетке на пересечении последней строки и последнего столбца, означает «поставку» четырех единиц продукции от третьего поставщика к «фиктивному» потребителю. Реально это означает, что четыре единицы продукции будут не востребованы и останутся у третьего поставщика невывезенными. Причем это происходит не из-за его большой мощности, а из-за его большой удаленности от потребителей, а, следовательно, невыгодности по сравнению с более близкими первым и вторым поставщиками.
Безусловно, план развития и размещения производства должен ориентироваться не только на минимум транспортных затрат, но и на минимум суммарных затрат на производство и транспортировку продукции. Пусть затраты на производство продукции у трех наших поставщиков составляют соответственно 4,3 и 1 р. Добавим эти производственные затраты построчно к показателям транспортных затрат в правых верхних углах клеток (разумеется, в «фиктивном» столбце остаются нулевые затраты). Решив задачу, получим следующий оптимальный план (см. табл. 4.11).
Таблица 4.11
|
Мощности поставщиков |
Потребности потребителей | |||
|
реальных |
фиктивного | |||
|
4 |
4 |
4 |
4 | |
|
3 |
1 |
6 |
1 3 |
0 |
|
3 |
2 |
5 |
3 1 |
0 2 |
|
10 |
3
|
4 4 |
10 |
0 2 |
Сравнивая два решения (табл. 4.10 и 4.11), видим, что низкие производственные затраты частично компенсировали невыгодность третьего поставщика с точки зрения затрат на транспортировку. Теперь востребовано 8 единиц его продукции. Для второго поставщика картина обратная. Что касается первого, то его наиболее дорогие производственные затраты в 4 р. не перевесили экономии на низких транспортных расходах, которую дает его использование.
С формальной математической стороны задача, представленная в табл. 4.11, по-прежнему является транспортной задачей. Однако с экономико-математической стороны, это - задача развития и размещения производства, в которой выбор пунктов и размеров производства осуществляется с позиций совокупных транспортао-произродственных затрат.
Отметим, что в закрытой транспортной задаче никакое построчное изменение затрат, т. е. прибавление или вычитание одного и того же числа из затрат по строке (столбцу), оптимального плана не изменит. Математически это достаточно тривиально, экономически же очевидно, что при равенстве суммарных потребностей потребителей и суммарных мощностей поставщиков вся продукция будет вывезена при любых производственных затратах, а план перевозок определится лишь на основе минимума только транспортных затрат. Открытая же задача дает возможность выбора.
§2. Однопродуктовые модели развития и размещения производства
Рассмотренная в разд. 4.2 задача развития и размещения являлась однопродуктовой, транспортно-производственной, безвариантной задачей.
Последняя запись соответствует примеру, приведенному в табл. 4.11. Вернемся к нему и рассмотрим третьего поставщика. Его удельные производственные затраты равны 1 р., т. е. считается, что они постоянны при любом плане развития и размещения производства.
Однако экономическая теория и практика свидетельствуют, что величина производственных затрат существенно зависит от объемов производства продукции, т. е. является функцией от нич. Как правило, концентрация производства приводит к снижению удельных производственных затрат вследствие экономии на накладных расходах и т. п. Соответственно, правомерно определять общую величину производственных затрат не как произведение единого норматива затрат на объем производства (линейная зависимость), а как произведение переменного норматива, представляющего собой функцию от размеров производства, на объем производства (нелинейная зависимость),
В этом примере третий поставщик вошел в оптимальный план развития и размещения с объемом производства не в 10, а в 8 ед, В связи с этим его удельные производственные затраты должны быть несколько отличны (больше) от 1 р. Таким образом, в нашем оптимальном плане имеет место искусственное занижение производственны); затрат у третьего поставщика, т. е. завышение его эффективности относительно других. Предположим, что при установлении мощности предприятия в третьем пункте не на максимальном уровне (10 ед.), а на уровне 8 ед., удельные производственные затраты повышаются с 1 до 2 р. Но до решения задачи мы не можем знать окончательного плана, а следовательно, и выбранного размера мощности. Кстати, даже приняв удельные производственные затраты третьего поставщика на уровне 2 р., приемлемого выхода из создавшейся ситуации не найдем, так как, увеличив в третьей строке затраты, получим несколько другой оптимальный план (такой же, как в табл. 4.10). В нем у третьего поставщика мощность уменьшится до 6 ед., и опять налицо несоответствие мощности и затрат.
Кроме того, мощность предприятия в третьем пункте на уровне 8 и (или) 6 ед. может быть нереальна ввиду отсутствия, например, именно таких типовых проектов.
Кроме того, при современном уровне развития техники в большинстве отраслей мощность предприятия зависит от единичной мощности основного технологического оборудования и числа единиц этого оборудования, формирующих производственную мощность конкретного предприятия. Неделимость производственных объектов (например, новых технологических линий), пребование возможно более полной загрузки их мощности ведет к дискретности производственных мощностей.
§3. Многопродуктовые модели развития и размещения производства
В многопродуктовых задачах развития и размещения производства определяются не только пункты нового строительства и расширения (реконструкции) действующих предприятий и размеры производства для них, но и объемы произзодства каждого продукта в рамках общей мощности предприятия (т. е. специализация).
Запишем много продуктовую задачу. Для этого введем следующие обозначения:
i - индекс пункта производства, i = 1,2.....m ;
j - индекс пункта потребления, j = 1,2,..., п ;
k — индекс вида продукции, k = 1,2..... i;
bkj - размер потребности пункта в продукции вида k;
at - максимально возможная мощность предприятия в пункте i;
tkif - затраты на перевозку единицы k-й продукции от i-го поставщика к j-му потребителю;
Ski - затраты на производство единицы продукции вида k в пункте i в части, зависящей от специализации;
Si - затраты на производство единицы продукции вида k в пункте i в части, зависящей от концентрации (т. е. от общей мощности предприятия в данном пункте);
xkif - объем перевозки продукции k от i-го поставщика к j-му потребителю;
xki - объем производства продукции вида k на i-м предприятии;
xi - общая мощность предприятия в пункте i.
Требуется минимизировать общий объем транспортно-производственных затрат
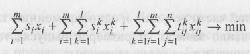 (4.47)
(4.47)
при выполнении следующих условий:
- потребность каждого потребителя должна быть удовлетворена по каждому виду продукции
![]() (4.48)
(4.48)
- размер вывоза от каждого из поставщиков по каждому из продуктов должен быть равен объему производства
![]() (4.49)
(4.49)
- суммарный выпуск всех видов продукции предприятия не должен превосходить максимально возможных размеров производства в данном пункте
![]() (4.50)
(4.50)
- неотрицательность переменных
xij £ 0(i = 1, 2, …, m; j = 1, 2, …, n; k = 1, 2, …, l);
xik ³ 0(i = 1, 2, …, m; k = 1, 2, …, l);
xi ³ 0(i = 1, 2, …, m); (4.51)
Отметим, что раздельный учет в критерии оптимальности (4.47) производственных затрат sj и skj вызван различным характером зависимости отдельных статей или категорий затрат от концентрации и специализации производства. Так, например, общезаводские расходы (в составе текущих затрат) и капитальные вложения в пассивную часть фондов (в составе единовременных затрат) зависят лишь от общей мощности предприятия (т. е. концентрации) и, как правило, мало зависят от структуры выпуска продукции по видам. Наоборот, затраты на сырье и на приобретение основного технологического оборудования служат примером той части текущих и единовременных затрат, которые непосредственно зависят от размеров выпуска того или иного вида продукции (т. е. от специализации).
Стандарты – ЧТО ДОЛЖНО БЫТЬ В ЛЕКЦИЯХ
Моделирование микроэкономических процессов и систем.
Методы анализа и прогнозирования рыночной конъюнктуры, определения потребительских свойств продукции и ее качества. Планирование маркетинговой политики. Методы оптимизации маркетинговых затрат (реклама, товародвижение и сбыт).
Моделирование ценовой политики. Производственные системы, их структура. Технологии производства и их представление в экономико-математических моделях. Оптимизация производственных процессов. Модели управления производственными запасами с учетом спроса и цен на продукцию. Моделирование инвестиций и анализ их эффективности.
Решение задач развития и размещения производства. Транспортно-производственные модели. Сетевые модели транспортных потоков. Моделирование и оптимизация работы предприятий.
Критерии оптимизации и основные ограничения, локальные и глобальные критерии.
Содержание
Тема 1. Методы анализа и прогнозирования рыночной конъюнктуры.. 2
§1. Прогнозирование на микроуровне. 2
§2. Методы моделирования и прогнозирования. 2
§3. Метод экономического анализа. 4
§4. Конъюнктура рынка. 4
Тема 2. Определение потребительских свойств продукции и её качества. 5
§1. Моделирование потребления. 5
§2. Задача оптимизации потребительского выбора. 7
§3. Выбор потребителя при заданной полезности. 8
§2. Оценка качества и конкурентоспособности товара. 9
§3. Методы оценки уровня качества товара. 10
§4. Оценка конкурентоспособности товара. 12
§5. Зависимость цены продукции от её качества. 13
Тема 3. Планирование маркетинговой политики. 15
§1. Планирование в маркетинговой деятельности. 15
§2. Методы решения задач планирования в условиях полной определенности. 17
§3. Методы многокритериальной оптимизации к решению задач планирования 19
§4. Принятие маркетинговых решений в условиях неопределенности. 20
Тема 4. Методы оптимизации маркетинговых затрат.. 22
§1. Реклама. 22
§2. Системы и каналы товародвижения и сбыта продукции. 25
§3. Модели отгрузки товаров фирмы через собственную сбытовую сеть. 27
Тема 5. Моделирование ценовой политики. 29
§1. Выбор целей ценовой политики. 29
§2. Ценовая политика. 30
§3. Методы ценообразования. 32
Тема 5. Производственные системы.. 33
§1. Производственные системы и их структура. 33
§2. Технологии производства и их представление в экономико-математических моделях 37
Другое с.106 МЭП Грачёв§3. Оптимизация производственного процесса. 39
Тема 6. Модели управления производственными запасами с учётом спроса и цен на продукцию 46
§1. Основная модель. 46
§2. Модель производственных поставок. 48
§3. Модель поставок со скидкой. 50
§4. Моделирование инвестиций и анализ их эффективности. 51
Тема 7. Решение задач развития и размещения производства. 59
§1. Оптимизационные модели развития и размещения производства. 59
§2. Однопродуктовые модели развития и размещения производства. 61
§3. Многопродуктовые модели развития и размещения производства. 62
Стандарты – ЧТО ДОЛЖНО БЫТЬ В ЛЕКЦИЯХ.. 64
Содержание. 65




