Предполагается, что синтезируемый регулятор строится в виде линейной обратной связи по вектору состояния x(t):
(12)
где матрица регулятора 
С учетом закона управления (12), векторное уравнение объекта (10), замкнутого обратной связью, имеет вид
где матрица замкнутой системы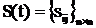 
определяется по формуле:
(13)
Критериальные условия (11) выполняются, если
(14)
Анализ показывает, что функциональные неравенства (14) удовлетворяются, если параметры sij(t) замкнутой САУ выбрать в следующем виде:
(15)
где вещественные параметры
(16)
Матрица K(t) регулятора, обеспечивающая выполнение соотношений (14), следовательно, и выполнение критериальных условий (11), определяется из матричного соотношения (13):
(17)
где элементы sij(t) матрицы S(t) определяются по формулам (15).
В результате справедлива следующая теорема.
Теорема 3. Пусть управляемый объект и алгоритм управления u(t) описываются, соответственно, соотношениями (10) и (12). Тогда, для выполнения критериальных условий (11), параметры замкнутой САУ должны определяться по формуле
а матрица регулятора должна удовлетворять матричному соотношению (17).
Таким образом, проблема синтеза регулятора для многомерной линейной нестационарной системы (10) сводится к решению матричного уравнения (17) относительно матрицы линейной обратной связи K(t).
В случае, когда m=n, а B(t) имеет обратную матрицу 
, матрица регулятора K(t) определяется в явной форме:
(18)
В противном случае, а также, когда B(t) не является квадратной, нахождение решения уравнения (17) можно осуществить на основе обобщенного 
обращения матрицы В:
Предложенный подход к синтезу линейных нестационарных САУ, по существу, является новым методом динамического проектирования автоматических регуляторов с переменной структурой (СПС). В отличие от подходов теории СПС, разработанный метод не предполагает организацию в системе режима скольжения. При этом, достижение цели управления обеспечивается за определенное количество переключений структуры регулятора, а условия устойчивости замкнутой САУ определяются теоремой 2, т. е. критериальными соотношениями (11). Техническая реализация матрицы регулятора, определяемая выражением (18), не вызывает особых трудностей.
Далее, рассматривается задача синтеза динамического регулятора для линейного нестационарного многомерного объекта, описываемого векторным уравнением (7).
Предполагается, что:
1) объект (7) обладает свойством управляемости;
2) все компоненты вектора состояния доступны для измерения;
3) структура синтезируемого динамического регулятора известна, его функционирование описывается векторным линейным уравнением:
, (19)
где M и D – матрицы искомого регулятора:
; 
.
Задача состоит в определении матриц M и D динамического регулятора, обеспечивающих заданные динамические свойства замкнутой САУ.
На основе теоремы 1, получено следующее уравнение синтеза динамики искомого регулятора:
, (20)
где L={lij}nхm и F={fij}nхn - вещественные матрицы, элементы которых определяются по следующим формулам:
,
.
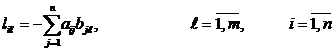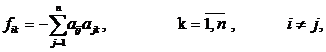
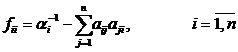В случае, когда 
, а B(t) имеет обратную матрицу 
, имеем, что
. (21)
Отсюда получаем, что искомые матрицы динамического регулятора определяются по следующим формулам:
. (22)
В противном случае, а также, когда B не является квадратной, нахождение решения уравнения (20) можно осуществить на основе обобщенного обращения В+ матрицы B. В этом случае искомые матрицы
, (23)
которые дают квазирешение уравнения (20).
Структура САУ с синтезированным динамическим регулятором показана на рис. 2.
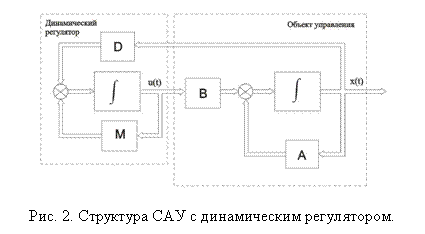
Алгоритм синтеза динамического регулятора включает следующие основные этапы:
Шаг 1. Задание модели объекта управления (7).
Шаг 2. Задание требований к динамическим свойствам проектируемой САУ (в частности, к быстродействию системы через времена регулирования 
).
Шаг 3. Выбор структуры закона функционирования (19) динамического регулятора.
Шаг 4. Формирование уравнения синтеза регулятора (20).
Шаг 5. Определение матриц M и D модели динамического регулятора по формуле (22) или (23).
Шаг 6. Компьютерное моделирование спроектированной замкнутой САУ и анализ качества переходных процессов.
В случае, если результаты моделирования показывают, что синтезированная САУ не обеспечивает заданные динамические свойства, то варьируются компоненты вектора настроечных параметров регулятора.
Далее, рассматривается задача синтеза наблюдающего устройства (рис. 3) полного порядка для линейного многомерного нестационарного объекта, динамика которого описывается векторным уравнением в переменных состояния (10). Вектор выхода объекта 
где его размерность 
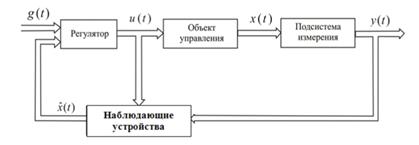
Рис. 3. Структура САУ с наблюдающим устройством.
Математическая модель линейного наблюдателя полного порядка (идентификатора) дается известным векторным уравнением:
, (24)
где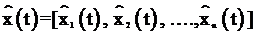 
– n-мерный вектор состояния идентификатора; 
– 
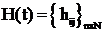-мерная матрица идентификатора.
Вводится вектор невязки
,
который определяет ошибку восстановления вектора состояния x(t).
Задача синтеза идентификатора для нестационарного линейного объекта (10) заключается в определении элементов матрицы 
, обеспечивающих стремление к нулю компонентов вектора ошибки идентификации 
, т. е.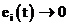 
, 
.
Для решения сформулированной задачи использована теорема 2. При этом, считается, что xi(t)=ei(t), i=
Алгоритм синтеза наблюдающего устройства получен на основе методики синтеза САУ с переменной структурой.
В четвертой главе теоретические результаты работы использованы для решения прикладных задач управления технологическими объектами.
Вначале, рассматривается технологический объект (рис. 4), предназначенный для намотки длинномерных материалов (лента, проволока и др.).
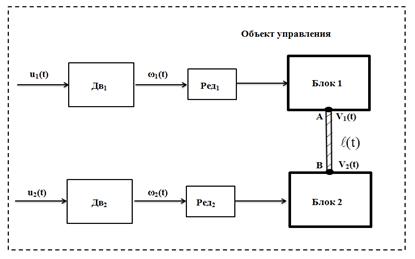
Рис. 4. Обобщенная схема объекта управления.
Обрабатываемый материал проходит через валки, установленные в Блоке 1 и наматывается на приемную катушку, которая представляет собой Блок 2. Вращение указанных функциональных элементов осуществляется двумя двигателями Дв1 и Дв2 через соответствующие редукторы (Ред1, Ред2). Основными технологическими переменными являются:
· линейные скорости V1(t) и V2(t) движения обрабатываемого материала на выходе Блока 1 и на входе Блока 2, т. е. в точках А и В соответственно;
· текущая длина обрабатываемого материала 
между точками A и B.
Управляющими воздействиями u1(t) и u2(t) являются напряжения, подаваемые на входы соответствующих усилителей мощности.
|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 |
