1. Недетерминированные алгоритмы
1.1. NP задачи
Все алгоритмы, рассматривавшиеся нами ранее, имели полиномиальную сложность. Главное, то, что мы могли найти точное решение этих задач за разумный промежуток времени. Все эти задачи относятся к классу Р — классу задач полиномиальной сложности. Такие задачи называются также практически разрешимыми.
Есть и другой класс задач: они практически неразрешимы и мы не знаем алгоритмов, способных решить их за разумное время. Эти задачи образуют класс NP — недетерминированной полиномиальной сложности. Отметим только, что сложность всех известных детерминированных алгоритмов, решающих эти задачи, либо экспоненциальна, либо факториальна. Сложность некоторых из них равна 2N, где N — количество входных данных. В этом случае при добавлении к списку входных данных одного элемента время работы алгоритма удваивается. Если для решения такой задачи на входе из десяти элементов алгоритму требовалось 1024 операции, то на входе из 11 элементов число операций составит уже 2048. Это значительное возрастание времени при небольшом удлинении входа.
Словосочетание «недетерминированные полиномиальные», характеризующее задачи из класса NP, объясняется следующим двухшаговым подходом к их решению. На первом шаге имеется недетерминированный алгоритм, генерирующий возможное решение такой задачи — что-то вроде попытки угадать решение; иногда такая попытка оказывается успешной, и мы получаем оптимальный или близкий к оптимальному ответ, иногда безуспешной (ответ далек от оптимального). На втором шаге проверяется, действительно ли ответ, полученный на первом шаге, является решением исходной задачи. Каждый из этих шагов по отдельности требует полиномиального времени. Проблема, однако, в том, что мы не знаем, сколько раз нам придется повторить оба эти шага, чтобы получить искомое решение. Хотя оба шага и полиномиальны, число обращений к ним может оказаться экспоненциальным или факториальным.
К классу NP относится задача о коммивояжере. Нам задан набор городов и «стоимость» путешествия между любыми двумя из них. Нужно определить такой порядок, в котором следует посетить все города (по одному разу) и вернуться в исходный город, чтобы общая стоимость путешествия оказалась минимальной. Эту задачу можно применять, например, для определения порядка эффективного сбора мусора из баков на улицах города или выбора кратчайшего пути распространения информации по всем узлам компьютерной сети. Восемь городов можно упорядочитьвозможными способами, а для десяти городов это число возрастает уже до 3 Поиск кратчайшего пути требует перебора всех этих возможностей. Предположим, что у нас есть алгоритм, способный подсчитать стоимость путешествия через 15 городов в указанном порядке. Если за секунду такой алгоритм способен пропустить через себя 100 вариантов, то ему потребуется больше четырех веков, чтобы исследовать все возможности и найти кратчайший путь. Даже если в нашем распоряжении имеется 400 компьютеров, все равно у них уйдет на это год, а ведь мы имеем дело лишь с 15 городами. Для 20 городов миллиард компьютеров должен будет работать параллельно в течение девяти месяцев, чтобы найти кратчайший путь. Ясно, что быстрее и дешевле путешествовать хоть как-нибудь, чем ждать, пока компьютеры выдадут оптимальное решение.
Можно ли найти кратчайший путь, не просматривая их все? До сих пор никому не удалось придумать алгоритм, который не занимается, по существу, просмотром всех путей. Когда число городов невелико, задача решается быстро, однако это не означает, что так будет всегда, а нас как раз интересует решение общей задачи.
Задача о коммивояжере, конечно, очень похожа на задачи про графы, которыми мы занимались в главе 5. Каждый город можно представить вершиной графа, наличие пути между двумя городами — ребром, а стоимость путешествия между ними — весом этого ребра. Отсюда можно сделать вывод, что алгоритм поиска кратчайшего пути решает и задачу коммивояжера, однако это не так. Какие два условия задачи о коммивояжере отличают ее от задачи о кратчайшем пути?
Во-первых, мы должны посетить все города, а алгоритм поиска кратчайшего пути дает лишь путь между двумя заданными городами. Если собрать путь из кратчайших кусков, выдаваемых алгоритмом поиска кратчайших путей, то он будет проходить через некоторые города по нескольку раз.
Второе отличие состоит в требовании возвращения в исходную точку, которое отсутствует в поиске кратчайшего пути.
Чтобы показать, что эта задача относится к классу NP, нам необходимо понять, как ее можно решить посредством описанной выше двухшаговой процедуры. В задаче о коммивояжере на первом шаге случайным образом генерируется некоторое упорядочивание городов. Поскольку это недетерминированный процесс, каждый раз будет получаться новый порядок. Очевидно, что процесс генерации можно реализовать за полиномиальное время: мы можем хранить список городов, генерировать случайный номер, выбирать из списка город с этим именем и удалять его из списка, чтобы он не появился второй раз. Такая процедура выполняется за O(N) операций, где N — число городов. На втором шаге происходит подсчет стоимости путешествия по городам в указанном порядке. Для этого нам нужно просто просуммировать стоимости путешествия между последовательными парами городов в списке, что также требует O(N) операций. Оба шага полиномиальны, поэтому задача о коммивояжере лежит в классе NP. Времяемкой делает ее именно необходимое число итераций этой процедуры.
Здесь следует отметить, что такую двухшаговую процедуру можно было применить к любой из рассматривавшихся нами ранее задач. Например, сортировку списка можно выполнять, генерируя произвольный порядок элементов исходного списка и проверяя, не является ли этот порядок возрастающим. Не относит ли это рассуждение задачу сортировки к классу NP? Конечно, относит. Разница между классом Р и классом NP в том, что в первом случае у нас имеется детерминированный алгоритм, решающий задачу за полиномиальное время, а во втором мы такого алгоритма не знаем.
Итак, задача принадлежит классу NP, если она разрешима за полиномиальное время недетерминированным алгоритмом. Как упоминалось, процесс сортировки можно реализовать следующим образом:
1) вывести элементы списка в случайном порядке;
2) проверить, что s < s+i для всех i от 1 до N — 1.
Это недетерминированный двухэтапный процесс. Первый этап не требует сравнений, и его можно выполнить за N шагов — по одному шагу на выходной элемент списка. Второй этап также полиномиален: для его выполнения необходимо сделать N - 1 сравнений. Такая процедура подходит под наше определение класса NP, и можно прийти к выводу, что задача сортировки принадлежит как классу Р, так и классу NP. То же самое можно проделать с любым полиномиальным алгоритмом, поэтому все задачи класса Р лежат и в классе NP, т. е. Р является подмножеством в NP. Однако в классе NP есть задачи, для которых мы не знаем полиномиального детерминированного алгоритма их решения.
Сутью этого различия является большое число вариантов, которые необходимо исследовать в NP задачах. Однако это число лишь незначительно превышает число комбинаций входных значений. У нас может быть список из 30 различных элементов или городов, и только один из 30! возможных порядков в этом списке является возрастающим или задает кратчайший путь. Разница же в том, что упорядочить список можно и полиномиальным алгоритмом — некоторым из них для этого понадобится всего 150 сравнений. В алгоритме пузырьковой сортировки при первом проходе по списку по крайней мере наибольший элемент встанет на свое место, отбросив тем самым всего за 29 сравнений по крайней мере 1/30 всех возможных комбинаций. На втором проходе 28 сравнений отбрасывают 1/29 часть оставшихся возможностей. При более внимательном взгляде видно, что число отброшенных возможностей может быть и большим: результатом каждого прохода может быть не только помещение на место наибольшего элемента списка, но и переупорядочивание других элементов.
Но наилучший известный нам способ поиска кратчайшего пути состоит в переборе всех возможных вариантов путей и сравнении их длин. У нас нет алгоритма, позволяющего успешно отбросить значительное количество вариантов. Вот нам и приходится просматривать их все. Даже при просмотре 1 из 30! путей в секунду нам понадобилось бы более 840 миллиардов веков для проверки всех путей.
Мы обсудим способы получения ответов, близких к оптимальному. При этом мы не можем оценить, насколько близок оптимальному полученный ответ, поскольку оптимальное значение нам неизвестно. Вместо этого мы можем продолжать исполнять алгоритм поиска приближенного решения: всякое новое решение будет лучше предыдущего. Может быть так мы доберемся и до оптимального решения, но гарантии этого отсутствуют.
Значит задача попадает в класс NP, если для ее решения необходимо рассмотреть огромное количество возможностей и у нас нет эффективного детерминированного алгоритма просеивания этих возможностей в поисках оптимального ответа.
Пример с задачей сортировки, которая решается как полиномиальным детерминированным, так и полиномиальным недетерминированным алгоритмом, подтверждает, что класс Р является подклассом в NP. Обсуждение различия между сортировкой и задачей коммивояжера должно, казалось бы, убедить Вас в том, что нам известны задачи из класса NP, не входящие в класс Р. Однако это не так. Нам известно только то, что пока не удалось найти детерминированного полиномиального алгоритма для всех задач из класса NP. Это не означает, что такого алгоритма не существует, и исследователи по-прежнему бьются над проблемой совпадения классов. Многие верят, что полиномиальные алгоритмы решения NP-полных задач не существуют, но как можно доказать, что не существует полиномиального алгоритма решения той или иной задачи? Лучше всего исследовать эту задачу и попробовать оценить снизу минимальный объем работы, необходимый для ее решения. Здесь, однако, мы и наталкиваемся на проблему получения нижней оценки, превышающей любой многочлен. Вопрос, выполняется ли равенство P=NP, до сих пор остается предметом исследования по всему миру.
1.2. Сведение задачи к другой задаче
Один из способов решения задач состоит в том, чтобы свести, или редуцировать, одну задачу к другой. Тогда алгоритм решения второй задачи можно преобразовать таким образом, чтобы он решал первую. Если преобразование выполняется за полиномиальное время и вторая задача решается за полиномиальное время, то и наша новая задача также решается за полиномиальное время.
Поясним наше рассуждение примером. Пусть первая задача состоит в том, чтобы вернуть значение «да» в случае, если одна из данных булевских переменных имеет значение «истина», и вернуть «нет» в противоположном случае. Вторая задача заключается в том, чтобы найти максимальное значение в списке целых чисел. Каждая из них допускает простое ясное решение, но предположим на минуту, что мы знаем решение задачи о поиске максимума, а задачу про булевские переменные решать не умеем. Мы хотим свести задачу о булевских переменных к задаче о максимуме целых чисел. Напишем алгоритм преобразования набора значений булевских переменных в список целых чисел, который значению «ложь» сопоставляет число 0, а значению «истина»— число 1. Затем воспользуемся алгоритмом поиска максимального элемента в списке. По тому, как составлялся список, заключаем, что этот максимальный элемент может быть либо нулем, либо единицей. Такой ответ можно преобразовать в ответ в задаче о булевских переменных, возвращая «да», если максимальное значение равно 1, и «нет», если оно равно 0.
В следующем разделе мы воспользуемся техникой сведения, чтобы кое-что узнать о NP задачах. Однако редукция NP задач может оказаться гораздо более сложной.
1.3. NP-полные задачи
При обсуждении класса NP следует иметь в виду, что наше мнение, согласно которому их решение требует большого времени, основано на том, что мы просто не нашли эффективных алгоритмов их решения. Может быть, посмотрев на задачу коммивояжера с другой точки зрения, мы смогли бы разработать полиномиальный алгоритм ее решения. Термин NP-noлная относится к самым сложным задачам в классе NP. Эти задачи выделены тем, что если нам все-таки удастся найти полиномиальный алгоритм решения какой-либо из них, то это будет означать, что все задачи класса NP допускают полиномиальные алгоритмы решения.
Мы показываем, что задача является NP-полной, указывая способ сведения к ней всех остальных задач класса NP. На практике эта деятельность выглядит не столь уж устрашающе — нет необходимости осуществлять редукцию для каждой NP задачи. Вместо этого для того, чтобы доказать NP-полноту некоторой NP задачи А, достаточно свести к ней какую-нибудь NP-полную задачу В. Редуцировав задачу В к задаче А, мы показываем, что и любая NP задача может быть сведена к А за два шага, первый из которых — ее редукция к В.
В предыдущем разделе мы выполняли редукцию полиномиального алгоритма. Посмотрим теперь на редукцию алгоритма, решающего NP задачу. Нам понадобится процедура, которая преобразует все составные части задачи в эквивалентные составные части другой задачи. Такое преобразование должно сохранять информацию: всякий раз, когда решение первой задачи дает положительный ответ, такой же ответ должен быть и во второй задаче, и наоборот.
Гамильтоновым путем в графе называется путь, проходящий через каждую вершину в точности один раз. Если при этом путь возвращается в исходную вершину, то он называется гамильтоновым циклом. Граф, в котором есть гамильтонов путь или цикл, не обязательно является полным. Задача о поиске гамильтонова цикла следующим образом сводится к задаче о коммивояжере, Каждая вершина графа — это город. Стоимость пути вдоль каждого ребра графа положим равной 1. Стоимость пути между двумя городами, не соединенными ребром, положим равной 2. А теперь решим соответствующую задачу о коммивояжере. Если в графе есть гамильтонов цикл, то алгоритм решения задачи о коммивояжере найдет циклический путь, состоящий из ребер веса 1. Если же гамильтонова цикла нет, то в найденном пути будет по крайней мере одно ребро веса 2. Если в графе N вершин, то в нем есть гамильтонов цикл, если длина найденного пути равна N, и такого цикла нет, если длина найденного пути больше N.
В книге Гэри и Джонсона, опубликованной в 1979 году, приведены сотни задач, NP-полнота которых доказана.
1.4. Типичные NP задачи
Каждая из задач, которые мы будем обсуждать, является либо оптимизационной, либо задачей о принятии решения. Целью оптимизационной задачи обычно является конкретный результат, представляющий собой минимальное или максимальное значение. В задаче о принятии решения обычно задается некоторое пограничное значение, и нас интересует, существует ли решение, большее (в задачах максимизации) или меньшее (в задачах минимизации) указанной границы. Ответом в задачах оптимизации служит полученный конкретный результат, а в задачах о принятии решений — «да» или «нет».
В 8.1 мы занимались оптимизационным вариантом задачи о коммивояжере. Это задача минимизации, и нас интересовал путь минимальной стоимости. В варианте принятия решения мы могли бы спросить, существует ли путь коммивояжера со стоимостью, меньшей заданной константы С. Ясно, что ответ в задаче о принятии решения зависит от выбранной границы. Если эта граница очень велика (например, она превышает суммарную стоимость всех дорог), то ответ «да» получить несложно. Если эта граница чересчур мала (например, она меньше стоимости дороги между любыми двумя городами), то ответ «нет» также дается легко. В остальных промежуточных случаях время поиска ответа очень велико и сравнимо со временем решения оптимизационной задачи. Поэтому мы будем говорить вперемешку о задачах оптимизации и принятия решений, используя ту из них, которая точнее отвечает нашим текущим целям.
1.4.1. Раскраска графа
Как мы уже говорили в главе 5, граф G = (V,E) представляет собой набор вершин, или узлов, V и набор ребер Е, соединяющих вершины попарно. Здесь мы будем заниматься только неориентированными графами. Вершины графа можно раскрасить в разные цвета, которые обычно обозначаются целыми числами. Нас интересуют такие раскраски, в которых концы каждого ребра окрашены разными цветами. Очевидно, что в графе с N вершинами можно покрасить вершины в N различных цветов, но можно ли обойтись меньшим количеством цветов? В задаче оптимизации нас интересует минимальное число цветов, необходимых для раскраски вершин графа. В задаче принятия решения нас интересует, можно ли раскрасить вершины в С или менее цветов.
У задачи о раскраске графа есть практические приложения. Если каждая вершина графа обозначает читаемый в колледже курс, и вершины соединяются ребром, если есть студент, слушающий оба курса, то получается весьма сложный граф. Если предположить, что каждый студент слушает 5 курсов, то на студента приходится 10 ребер. Предположим, что на 3500 студентов приходится 500 курсов. Тогда у получившегося графа будет 500 вершин иребер. Если на экзамены отведено 20 дней, то это означает, что вершины графа нужно раскрасить в 20 цветов, чтобы ни у одного студента не приходилось по два экзамена в день.
Разработка бесконфликтного расписания экзаменов эквивалентна раскраске графов. Однако задача раскраски графов принадлежит к классу NP, поэтому разработка бесконфликтного расписания за разумное время невозможна. Кроме того при планировании экзаменов обычно требуется, чтобы у студента было не больше двух экзаменов в день, а экзамены по различным частям курсам назначаются в один день. Очевидно, что разработка «совершенного» плана экзаменов невозможна, и поэтому необходима другая техника для получения по крайней мере неплохих планов.
1.4.2. Раскладка по ящикам
Пусть у нас есть несколько ящиков единичной емкости и набор объектов различных размеров s1, s2,…, sn - В задаче оптимизации нас интересует наименьшее количество ящиков, необходимое для раскладки всех объектов, а в задаче принятия решения — можно ли упаковать все объекты в В или менее ящиков.
Эта задача возникает при записи информации на диске или во фрагментированной памяти компьютера, при эффективном распределении груза на кораблях, при вырезании кусков из стандартных порций материала по заказам клиентов. Если, например, у нас есть большие металлические листы и список заказов на меньшие листы, то естественно мы хотим распределить заказы как можно плотнее, уменьшив тем самым потери и увеличив доход.
1.4.3. Упаковка рюкзака
У нас имеется набор объектов объемом s1,..., sn стоимости w1,..., wn, В задаче оптимизации мы хотим упаковать рюкзак объемом К так, чтобы его стоимость была максимальной. В задаче принятия решения нас интересует, можно ли добиться, чтобы суммарная стоимость упакованных объектов была по меньшей мере W.
Эта задача возникает при выборе стратегии вложения денег: объемом здесь является объем различных вложений, стоимостью — предполагаемая величина дохода, а объем рюкзака определяется размером планируемых капиталовложений.
1.4.4. Задача планирования работ
Пусть у нас есть набор работ, и мы знаем время, необходимое для завершения каждой из них, t1, t2,..., tN, сроки d1,d2,... , dN, к которым эти работы должны быть обязательно завершены, а также штрафы P1, P2 ,…,Pn которые будут наложены при незавершении каждой работы в установленные сроки. Задача оптимизации требует установить порядок работ, минимизирующий накладываемые штрафы. В задаче принятия решений мы спрашиваем, есть ли порядок работ, при котором величина штрафа будет не больше Р.
1.5. Двухшаговое решение NP-задач
Описание класса NP предполагает, что у задач этого класса есть решение с недетерминированным первым шагом, на котором генерируется возможный ответ, и детерминированным вторым шагом, который сгенерированный ответ проверяет. Оба эти шага выполняются за полиномиальное время. Мы займемся алгоритмами, проверяющими полученный ответ в задачах о планировании работ и о раскрашивании графа.
1.5.1. Задача о планировании работ
Напомним, что в задаче о планировании работ задан набор работ, которые необходимо выполнить. Для каждой работы известно, сколько времени необходимо на ее выполнение, срок, к которому ее следует завершить, и штраф, накладываемый в случае ее незавершения к назначенному сроку. Работы выполняются последовательно, а сроки окончания отсчитываются с момента начала первой работы. Для каждой работы нам известна четверка (n, t, d, p), где n — номер работы, t — занимаемое ею время, d — срок окончания, р — штраф. Вот пример списка из пяти работ: {(1,3,5,2), (2,5, 7,4), (3,1, 5, 3), (4,6,9,1), (5,2,7,4)}.
В задаче принятия решения задается некоторое значение Р, и мы хотим узнать, существует ли такой порядок работ, при котором суммарный штраф не превысит Р. В задаче оптимизации нас интересует минимальное значение суммарного штрафа. Мы займемся задачей принятия решений: если несколько раз вызвать алгоритм решения этой задачи с возрастающей границей Р, пока мы не получим утвердительный ответ, то мы решим заодно и задачу оптимизации. Другими словами, мы спрашиваем, существует ли порядок работ с штрафом 0. Если такого порядка нет, то мы переходим к штрафу 1, и будем увеличивать размер штрафа до тех пор, пока не получим утвердительного ответа. Следующий алгоритм сравнивает с порогом возможное решение задачи планирования работ.
PenaltyLess(list, N,limit)
list упорядоченный список работ
N общее число работ
limit предельная величина штрафа
currentTime=0
currentPenalty=0
currentJob=l
while (currentJob<=N) and (currentPenalty<=limit)
currentTime += list[currentJob].time;
if(list[currentJob].deadline<currentTime) // срок окончания работы
currentPenalty + = list[currentJob].penalty;
end if;
currentJob=curreatJob+1;
end while;
if currentPenalty <= limit
return да
else
return нет
end if;
end.
Принадлежность задачи классу NP требует проверки предложенного решение за полиномиальное время. Видно, что описанный алгоритм действительно подсчитывает суммарный штраф. Анализ временной сложности показывает, что цикл while совершает не более N проходов; максимум достигается, если значение переменной currentPenalty не превышает предельное. Учет всех операций позволяет заключить, что общее число сравнений равно 3N + 1, а число сложений равно 3N. Это означает, что сложность алгоритма равна O(N), и значит он полиномиален и удовлетворяет определению класса NP.
1.5.2. Раскраска графа
В задаче о раскраске графа требуется найти способ раскраски вершин графа в несколько цветов (занумерованных целыми числами) таким образом, чтобы любые две соседние вершины были покрашены в различные цвета. Принятие решения заключается в том, чтобы установить, можно ли покрасить вершины в С или меньше цветов с соблюдением указанного требования, а оптимизация — в том, чтобы найти минимально необходимое число цветов.
На недетерминированном этапе генерируется возможное решение, представляющее собой список вершин и приписанных к ним цветов. Именно на этом этапе решается, сколько будет использовано цветов, поэтому этап проверки не несет ответственности за выбранное число цветов. При выборе решения недетерминированный этап попробует обойтись С цветами. В задаче оптимизации он может начать с большого числа цветов, последовательно уменьшая их количество, пока требуемая раскраска еще возможна. Обнаружив, что граф нельзя раскрасить в X цветов, мы заключим, что раскраска в X + 1 цвет является минимально возможной.
Нижеследующий алгоритм проверяет, является ли сгенерированная раскраска допустимой. Раскрашиваемый граф представлен в виде списка примыканий, элемент graph [j] этого списка описывает j-ую вершину графа, поле graph [j].edgeCount этого элемента — число выходящих из нее ребер, а поле graph[j] .edge является массивом, в котором хранятся вершины, соседние с вершиной j.
bool ValidColoring(graph, N,colors)
graph, список примыканий
N число вершин в графе
colors массив, сопоставляющий каждой вершине ее цвет
for j=l to N //для каждой вершины графа
for k=l to graph[j].edgeCount // проверка на несовпадение с цветом
if (colors[j] == colors[graph[j].edge[k]]) //смежной вершины
return нет
end if ;
end for ;
end for ;
return да
end.
Видно, что этот алгоритм правильно проверяет допустимость раскраски. Он проходит по всем вершинам, и если вершина непосредственно связана с другой того же цвета, то алгоритм останавливается и возвращает отрицательный ответ. Если же все пары соседних вершин окрашены различными цветами, то ответ утвердительный. Что касается временной сложности этого алгоритма, то внешний цикл for осуществляет TV проходов. Во внутреннем цикле просматривается каждое ребро, выходящее из данной вершины. Поэтому общее число сравнений будет равно числу ребер, т. е. сложность алгоритма равна O(edges) — очевидно полиномиальная оценка, поскольку число ребер в графе не превосходит N2. Поэтому наши требования оказываются выполненными.
1.6. Приложение задач класса NP
Задачи из класса NP имеют большое число приложений, поэтому их решение представляет значительный интерес. Поскольку полиномиальные алгоритмы решения этих задач неизвестны, следует рассмотреть альтернативные возможности, дающие лишь достаточно хорошие ответы. Такой алгоритм может иногда дать и оптимальный ответ, однако такую счастливую случайность нельзя предусмотреть. Мы изучим некоторое количество приближенных алгоритмов решения этих задач.
1.6.1. Жадные приближенные алгоритмы
Изучим несколько жадных алгоритмов, приближенно решающих задачи из класса NP.
Как уже обсуждалось, найти точное решение задачи из класса NP трудно, потому что число требующих проверки возможных комбинаций входных значений чрезвычайно велико. Для каждого набора входных значений I мы можем создать множество возможных решений PSI. Оптимальное решение это такое решение Soptimal ÎPSI, что Value(Soptimal) £ Value(S’) для всех S' ÎPSI, если мы имеем дело с задачей минимизации, и Value(Soptimal) ³ Value(S') для всех S'ÎPSI, если мы имеем дело с задачей максимизации.
Решения, предлагаемые приближенными алгоритмами для задач класса NP, не будут оптимальными, поскольку алгоритмы просматривают только часть множества PSI, зачастую очень маленькую. Качество приближенного алгоритма можно определить, сравнив полученное решение с оптимальным. Иногда оптимальное значение — например, минимальную длину пути коммивояжера — можно узнать, и не зная оптимального решения — самого пути. Качество приближенного алгоритма при этом дается дробью

Иногда будет играть роль, рассматриваем ли мы случаи с фиксированным числом входных значений или случаи с общим оптимальным решением. Другими словами, хотим ли мы понять, насколько хорош приближенный алгоритм на входных списках длины 10 или на входных списках различной длины с оптимальным значением 50? Эти две точки зрения могут привести к различным результатам.
Приводимые алгоритмы являются не единственно возможными, скорее они призваны продемонстрировать многообразие различных подходов. Все эти приближенные алгоритмы полиномиальны по времени.
1.6.2. Приближения в задаче о коммивояжере
Для решения многих задач (в том числе и из класса Р) пригодны так называемые жадные алгоритмы. Эти алгоритмы пытаются сделать наилучший выбор на основе доступной информации. Напомним, что алгоритмы построения минимального остовного дерева и кратчайшего пути являются примерами жадных алгоритмов.
Сначала кажется, что для решения задачи о коммивояжере можно просто воспользоваться алгоритмом поиска кратчайшего пути, однако ситуация не так проста. Алгоритм Дейкстры предназначен для поиска кратчайшего пути между двумя вершинами, но найденный путь не обязательно проходит через все вершины графа. Однако можно воспользоваться этим общим подходом для построения жадного приближенного алгоритма. Стоимость проезда между городами можно задать матрицей примыканий; пример такой матрицы приведен на рис. 8.1.
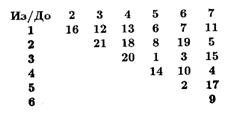
Рис. 8.1. Матрица примыканий для полного взвешенного графа
Эта матрица верхняя треугольная, поскольку стоимость проезда между городами i и j одинакова в обоих направлениях. Еели бы мы выписали все стоимости, то нижний треугольник матрицы попросту совпал бы с верхним. Использование верхнетреугольной матрицы позволяет упростить трассировку алгоритма.
Наш алгоритм будет перебирать набор ребер в порядке возрастания всех весов. Он не будет формировать путь; вместо этого он будет проверять, что добавляемые к пути ребра удовлетворяют двум условиям:
1) При добавлении ребра не образуется цикл, если это не завершающее ребро в пути.
2) Добавленное ребро не является третьим, выходящим из какой-либо одной вершины.
В примере с рис. 8.1 мы выберем первым ребро (3,5), поскольку у него наименьший вес. Следующим выбранным ребром будет (5,6). Затем алгоритм рассмотрит ребро (3,6), однако оно будет отвергнуто, поскольку вместе с двумя уже выбранными ребрами образует цикл [3, 5, 6, 3], не проходящий через все вершины. Следующие два ребра (4,7) и (2,7) будут добавлены к циклу. Затем будет рассмотрено ребро (1,5), но оно будет отвергнуто, поскольку это третье ребро, выходящее из вершины 5. Затем будут добавлены ребра (1,6) и (1,4). Последним добавленным ребром будет (2,3). В результате мы получим циклический путь [1, 4, 7, 2, 3, 5, 6, 1], полная длина которого 53, Это неплохое приближение, однако заведомо не оптимальное решение: есть по крайней мере один более короткий путь, [1, 4, 7, 2, 5, 3, 6, 1], полная длина которого 41.
1.6.3. Приближения в задаче о раскладке по ящикам
Один из подходов к получению приближенного решения задачи о раскладке по ящикам предлагает упаковывать первый подходящий предмет. Стратегия состоит в том, что ящики просматриваются поочередно пока не найдется ящик, в котором достаточно свободного места для упаковки очередного предмета. Как, например, будет происходить упаковка предметов размером (0.5, 0.7, 0.3, 0.9, 0.6, 0.8, 0.1, 0.4, 0.2, 0.5)? Видно, что в первый ящик попадут предметы размером [0.5, 0.3, 0.1], во второй — предметы размером [0.7, 0.2], в третий — предмет размером [0.9], в четвертый — предметы размером [0.6, 0.4], в пятый — [0.8], и, наконец, в шестой — предмет размером [0.5]. Эта упаковка не оптимальна, потому что возможна упаковка в пять ящиков: [0.9, 0.1], [0.8, 0.2], [0.7, 0.3], [0.6, 0.4] и [0.5,0.5]. Вот алгоритм укладки в первый подходящий ящик.
FirstFit(size, N, Used)
size список размеров предметов
N число предметов
Used положения разложенных предметов
for i=l to N
Used[i]=0 ;
end for;
for item=l to N
binLoc=l;
while Used [binLoc]+size[item]>1 //ищет место в ящике для
binLoc=binLoc+l; // очередного предмета
end while;
Used [binLoc] +=size[item] ;
end for;
end.
В другом варианте этого алгоритма список предметов сначала сортируется по убыванию размера, а затем они раскладываются поочередно в первый подходящий ящик. Читатель без труда проверит, что в рассмотренном примере модифицированный алгоритм приведет к оптимальному решению. Однако модифицированный алгоритм не всегда приводит к лучшим результатам, чем обычный. Рассмотрим набор предметов размеров (0.2, 0.6, 0.5, 0.2, 0.8, 0.3, 0.2, 0.2). Обычная раскладка в первый подходящий ящик приводит к оптимальной раскладке в три ящика. Начав с сортировки списка, мы получим список (0.8, 0.6, 0.5, 0.3, 0.2, 0.2, 0.2, 0.2). Раскладка в первый подходящий ящик отсортированного списка приведет к раскладке по ящикам [0.8, 0,2], [0.6, 0.3], [0.5, 0.2, 0.2] и [0.2], использующей на один ящик больше оптимального решения.
Анализ показывает, что стратегия укладки в первый подходящий ящик по отсортированному списку приводит к числу ящиков, превышающему оптимальное в среднем на 50%. Это означает, что если, скажем, для оптимальной укладки достаточно 10 ящиков, то результат алгоритма будет около 15. Если список предварительно не отсортирован, то дополнительные расходы составят в среднем 70%, т. е. при оптимальном числе ящиков 10 алгоритм сгенерирует укладку в 17 ящиков.
1.6.4. Приближения в задаче об упаковке рюкзака
Приближенный алгоритм упаковки рюкзака представляет собой простой жадный алгоритм, выбирающий наилучшее отношение стоимости к размеру. Сначала мы сортируем список объектов по отношению стоимости к размеру. Каждый объект представляется в виде пары [размер, стоимость]. Для списка объектов ([25, 50], [20, 80], [20, 50], [15, 45], [30, 105], [35, 35], [20, 10], [10, 45]) удельные стоимости имеют значения (2, 4, 2.5, 3, 3.5, 1, 0.5, 4.5). Сортировка удельных стоимостей приводит к списку ([10, 45], [20, 80], [30, 105], [15, 45], [20, 50], [25,50], [35, 35], [20, 10]). После этого мы начинаем заполнять рюкзак последовательно идущими элементами отсортированного списка объектов. Если очередной объект не входит — мы отбрасываем его и переходим к следующему; так продолжается до тех пор, пока рюкзак не заполнится или список объектов не будет исчерпан. Таким образом, если емкость рюкзака 80, то мы сможем поместить в него первые четыре предмета суммарного объема 75 и общей стоимостью 275. Это не оптимальное решение: первые три предмета с добавкой пятого дают суммарный объем 80 и стоимость 280.
1.6.5. Приближения в задаче о раскраске графа
Раскраска графа — необычная задача: как мы уже упоминали ранее, построение раскраски, достаточно близкой к оптимальной, дается столь же сложно, как и построение оптимальной раскраски. Число красок, даваемое наилучшим известным полиномиальным алгоритмом, более чем вдвое превышает оптимальное. Кроме того доказано, что если существует полиномиальный алгоритм, раскрашивающий вершины любого графа числом красок, превышающим оптимальное не более чем вдвое, то существует и полиномиальный алгоритм оптимальной раскраски любого графа. Существование такого алгоритма означало бы, что P=NP. На сложность графа можно наложить некоторые условия, облегчающие его раскраску. Например, известны полиномиальные алгоритмы раскраски планарных графов, т. е. таких графов, которые можно изобразить на плоскости в виде набора вершин и ребер, представленных попарно не пересекающимися дугами.
Вот простой алгоритм последовательной раскраски произвольного графа с N вершинами.
ColorGraph(G)
G раскрашиваемый граф
for i=l to N
c=l ;
while в G есть вершина, соседняя с вершиной i,
покрашенная цветом с
с=с+1;
end while;
покрасить вершину i цветом с
end for;
end.
Степенью графа называется наибольшее число ребер, выходящее из одной вершины. Число С красок, используемое приведенным алгоритмом, равно степени графа, увеличенной на единицу. Можно достичь и лучшего результата.
2. Вероятностные алгоритмы
Подход, используемый в вероятностных алгоритмах, в корне отличается от детерминированного подхода в алгоритмах из глав 1-8. В некоторых ситуациях вероятностные алгоритмы позволяют получить результаты, которых нельзя достигнуть обычными методами.
2.1. Численные вероятностные алгоритмы
Численные вероятностные алгоритмы предназначены для получения приблизительных ответов на некоторые математические вопросы. Чем дольше работает такой алгоритм, тем точнее полученный ответ.
2.1.1. Игла Бюффона
Предположим, что у Вас есть 355 одинаковых палочек, длина каждой из которых равна половине ширины доски дощатого пола. Сколько палочек пересечет щели между досками пола, если их подбросить и дать упасть на пол? Это может быть любое число между 0 и 355, однако Джордж Луис Леклерк показал, что в среднем число таких палочек будет почти в точности равно 113. Для каждой палочки вероятность пересечь щель равна 1/π. Объясняется такая величина соотношением между возможным углом поворота упавшей палочки и расстоянием между щелями. Для палочки, упавшей перпендикулярно к щелям, вероятность пересечения щели равна одной второй (это отношение длины палочки к ширине доски пола). Если, однако, палочка упала параллельно доске, то она почти наверняка не пересекает щель. Поэтому число π можно вычислять, подбрасывая палочки и подсчитывая, сколько из них пересекло щели. Отношение общего числа палочек к числу тех из них, что пересекли щели, будет приближением числа π.
Аналогичный способ приближенного подсчета числа π заключается в бросании стрелок в мишень, представляющую собой квадрат, в который вписан круг (рис. 10.1). Мы выбираем точки в квадрате случайным образом и подсчитываем, какая их часть попала в круг. Если радиус круга равен г, то его площадь равна πг2, а площадь квадрата равна (2г)2 = 4г2. Отношение площади круга к площади квадрата равно π /4. Если мы выбираем точки в квадрате действительно случайно, то стрелки распределятся по квадрату более или менее равномерно. Для случайного бросания стрелок в мишень число π приблизительно равно 4 * c/s, где с — число стрелок, попавших в круг, а s — общее число брошенных стрелок. Чем больше стрелок брошено, тем более точное приближение к числу π мы получаем.
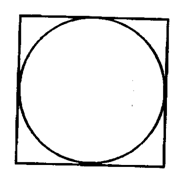
Рис. 10.1. Круг, вписанный в квадрат
С помощью этой техники можно подсчитать площадь произвольной неправильной фигуры, для которой мы умеем проверять, принадлежит ли ей заданная точка (х, у). Для этого мы просто генерируем случайные точки в объемлющем фигуру квадрате и подсчитываем отношение числа тех из них, которые попали внутрь фигуры, к общему числу сгенерированных точек. Отношение:
совпадает с отношением
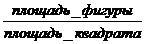
2.1.2. Вычисление интеграла функции f
Напомним, что для положительной непрерывной функции f площадь под ее графиком называется интегралом этой функции. Интегралы некоторых функций трудно или невозможно вычислять аналитически, однако их можно подсчитать приблизительно, воспользовавшись техникой бросания стрелок. Для иллюстрации этого метода ограничимся частью графика функции f, заключенной между положительными полуосями координат и прямыми х = 1 и у = 1 (см. рис. 10.1). Нетрудно обобщить рассмотрение на произвольный ограничивающий прямоугольник.
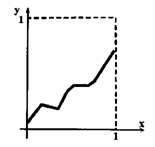
Рис.10.2. График функции, ограниченный осями х и у и прямыми х = 1 и у=1
Бросаем стрелки в квадрат случайным образом и подсчитываем, сколько из них оказались под графиком. Отношение числа стрелок под графиком к общему числу брошенных стрелок будет приблизительно равно площади под графиком функции. Как и в предыдущих случаях, чем больше стрелок мы бросим, тем точнее окажется приближение. Вот как выглядит соответствующий алгоритм:
Integrate(f, dartCount)
f интегрируемая функция
dartCount число бросаемых стрелок
hits=0;
for i=l to dartCount
x=uniform(0,l); //генерация случайного числа
y=uniform(0,l);
if y<=f(x)
hits=hits+l;
end if ;
end for ;
return hits/dartCount;
end.
2.1.3. Вероятностный подсчет
Как хорошо известно, можно держать пари, что в компании из 25 случайно выбранных людей есть по крайней мере двое с совпадающим днем рождения. Хотя на первый взгляд такое пари может показаться глупым, вероятность его выигрыша составляет 56%. В общем случае имеется N!/(N — k)! способов выбрать k различных объектов в множестве из N объектов, если порядок выбора играет роль. Если же позволяются повторения, то число возможностей увеличивается до Nk. Используя эти сведения, мы заключаем, что вероятность выиграть пари равна 1 — 365!/(340! * 36525). На практике вероятность выигрыша даже выше, поскольку приведенное рассуждение не учитывает того, что дни рождения распределены по году неравномерно. Выписанное число не так-то легко вычислить, как нелегко решить и обратную задачу: сколько выборок нужно сделать из N-элементного множества прежде, чем мы повторно выберем один и тот же элемент? Другими словами, если в году 365 дней, то сколько людей надо взять, чтобы вероятность того, что среди них найдутся двое с одинаковым днем рождения, была достаточно велика? Для приближенного подсчета таких чисел можно применить следующий алгоритм:
ProbabilityCount(H)
k=0;
s={};
a=uniform(l, N); //генерация случайного числа
do
k=k+l;
s=s+{a};
a=uniforin(l, N) ;
while a not in s
return k;
end.
Эта функция генерирует случайное число между 1 и N до тех пор, пока какое-либо из чисел не будет сгенерировано повторно. Для получения более точного результата ее можно запускать несколько раз, а полученные ответы усреднять. В примере с днями рождения (N = 365) выдаваемые ответы будут близки к 25.
2.1.4. Алгоритмы Монте Карло
Алгоритмы Монте Карло всегда выдают какие-либо результаты, однако вероятность того, что результат правильный, возрастает при увеличении времени работы алгоритма. Иногда такие алгоритмы возвращают неправильные ответы. Алгоритм называется правильным, если он возвращает правильный ответ с вероятностью р (1/2 < р < 1). Если число правильных ответов на данном входе превышает единицу, то алгоритм Монте Карло называется стойким, если возвращаемый им правильный ответ всегда один и тот же.
Результаты алгоритма Монте Карло можно улучшить двумя способами. Во-первых, можно увеличить время его работы. Во-вторых, можно повторять его несколько раз. Вторая возможность реализуется только, если алгоритм стойкий. В этом случае алгоритм можно вызывать много раз и выбирать тот ответ, который встречается чаще всего. Подобные действия могут выглядеть приблизительно так:
Monte3(x)
one=Monte(x);
two=Monte(x);
three=Monte(x);
if one==two || one==three
return one;
else
return two ;
end if;
end.
Этот алгоритм возвращает первое сгенерированное значение в том случае, если оно появляется среди ответов по крайней мере дважды. Если же это не так, то алгоритм возвращает второе значение: либо оно совпадает с третьим, либо все три значения различны, и тогда все равно, какое возвращать. Поскольку вероятность возвращения алгоритмом Монте Карло правильного ответа превышает половину, маловероятно, чтобы все три ответа оказались различными. Процедура MonteS превращает стойкий 80%-правильный алгоритм Монте Карло в 90%-правильный. Такой подход к повышению правильности алгоритма не всегда является наилучшим.
Рассмотрим алгоритм Монте Карло принятия решения, возвращаемый которым отрицательный ответ оказывается правильным в 100% случаев, и только в случае положительного ответа могут встречаться ошибки, т. е. в случае положительного ответа правильный ответ может быть как положительным, так и отрицательным. Это означает, что полученный алгоритмом отрицательный ответ должен рассматриваться как окончательный, а повторные вызовы функции призваны лишь искать серии положительных ответов, чтобы увеличить вероятность того, что это действительно правильный ответ.
Вот как выглядит такой алгоритм:
MultipleMonte(x)
if not Monte(x)
return false ;
end if ;
if not Monte(x)
return false ;
end if ;
return Monte(x);
end.
Такой алгоритм возвращает положительный ответ только в случае получения трех положительных ответов подряд. Если исходный алгоритм Монте Карло выдавал правильный положительный ответ лишь в 55% случаев, то описанная функция повышает вероятность правильных положительных ответов до 90%. Такое улучшение возможно и для численных алгоритмов, склонных выдавать одно и то же число.
2.1.5. Элемент, образующий большинство
Описанную выше технику можно применить к задаче проверки, есть ли в массиве элемент, образующий большинство. Это элемент, записанный более, чем в половине ячеек массива. Очевидный способ решения этой задачи требует порядка O(N2) сравнений, поскольку нам потребуется сравнить каждый элемент со всеми остальными. Но для ее решения известен и линейный алгоритм, похожий на алгоритм выборки из главы 2, поэтому приводимый ниже алгоритм Монте Карло призван лишь проиллюстрировать применяемую технику.
Majority(list, N)
list список элементов
N число элементов в списке
choice=uniform(l, N); //генерация случайного числа
count=0;
for i=l to N
if list [i]=list[choice]
count=count+l;
end if ;
end for ;
return (count>n/2);
end.
Эта функция выбирает случайный элемент списка и проверяет, занимает ли он больше половины ячеек. Этот алгоритм смещен к утвердительному ответу: если функция возвращает утвердительный ответ, то это означает, что мы нашли элемент, представляющий большинство списка. Однако, если возвращается отрицательный ответ, то возможно, что мы просто выбрали неправильный элемент. Если в массиве есть элемент, образующий большинство, то вероятность выбрать элемент из меньшинства меньше половины, причем она тем меньше, чем представительнее большинство. Таким образом, алгоритм возвращает правильный ответ не менее, чем в 50% случаев. Если вызвать функцию Majority пять раз, то правильность алгоритма возрастает до 97%, а его сложность будет 5N, т. е. она имеет порядок N.
2.1.6. Алгоритм Монте Карло проверки числа на простоту
Проверить, является ли данное число N простым, можно алгоритмом Монте Карло. В этом случае мы генерируем случайное число между 2 и ![]() и проверяем, делится ли N на это число. Если да, то число N составное, в противном случае мы не можем ничего сказать. Это не очень хороший алгоритм, потому что он возвращает отрицательный ответ слишком часто. Например, для числа, которое является произведением трех простых чисел 23, 43 и 61, алгоритм будет генерировать случайное число между 2 и 245, но только три числа из этого интервала привели бы к правильному результату. Вероятность успеха всего 1.2%.
и проверяем, делится ли N на это число. Если да, то число N составное, в противном случае мы не можем ничего сказать. Это не очень хороший алгоритм, потому что он возвращает отрицательный ответ слишком часто. Например, для числа, которое является произведением трех простых чисел 23, 43 и 61, алгоритм будет генерировать случайное число между 2 и 245, но только три числа из этого интервала привели бы к правильному результату. Вероятность успеха всего 1.2%.
Хотя этот простой алгоритм работает и не очень хорошо, имеются аналогичные подходы к проверке простоты числа, основанные на той же идее и дающие большую вероятность правильного ответа. В этой книге мы их не рассматриваем.
2.1.7. Алгоритмы Лас Вегаса
Алгоритмы Лас Вегаса никогда не возвращают неправильный ответ, хотя иногда они не возвращают вообще никакого ответа. Чем дольше работают эти алгоритмы, тем выше вероятность того, что они вернут правильный ответ. Алгоритм Лас Вегаса принимает случайное решение, а затем проверяет, приводит ли это решение к успеху. Программа, использующая алгоритм Лас Вегаса, вызывает его раз за разом, пока он не достигнет результата. Если обозначить через success(x) и failure(x) время, необходимое для того, чтобы получить соответственно положительный или отрицательный ответ на входных данных длины х, а через р(х) вероятность успешного завершения работы алгоритма, то мы приходим к равенству
time(x) = р(х) * success(x) + (1 — р(х)) * (failure(x) + time(x)).
Это равенство означает, что в случае успеха затраченное время совпадает с временем получения успешного результата, а в случае неудачи затраченное время равно сумме времени на достижение неудачного результата и еще на один вызов функции. Решая это уравнение относительно times(x), мы получаем
time(x) = success(x) + ((1 - p(x))/p(x)) * failure(x)
Эта формула означает, что время выполнения зависит от времени получения успешного результата, безуспешного результата и вероятности каждого из этих исходов. Интересно, что при убывании вероятности р(х) успешного результата время выполнения все равно может быть невысоким, если скорость получения безуспешного результата возрастает. Поэтому эффективность можно повысить, если быстрее получать безуспешный результат.
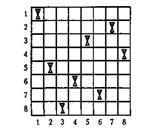
Рис. 10.3. Одно из решений задачи о восьми ферзях
Обратимся к задаче о расстановке восьми ферзей на шахматной доске так, чтобы они не били друг друга.
На рис. 10.3 изображено одно из решений этой задачи. Рекурсивный алгоритм ее решения помещает ферзя в первой клетке первой вертикали, а затем вызывает себя для того, чтобы поставить ферзя на вторую горизонталь. Если в какой-то момент алгоритму не удается найти положения для очередного ферзя на очередной горизонтали, то алгоритм возвращается на предыдущий шаг и пробует другое размещение ферзя на предыдущей строке.
Имеется вероятностная альтернатива детерминированному рекурсивному алгоритму. Мы можем поочередно размещать ферзей на доске случайным образом на очередной свободной горизонтали доски. Отличие алгоритма Лас Вегаса от стандартного рекурсивного алгоритма состоит в том, что при невозможности разместить очередного ферзя алгоритм попросту сдается и сообщает о неудаче. Рекурсивный же алгоритм пытается добиться положительного результата. Вот как выглядит алгоритм Лас Вегаса для расстановки восьми ферзей:
Queens(result)
result содержит номера вертикалей для ферзей
с соответствующих горизонталей
возвращает 1 в случае успеха и 0 в случае неудачи
row=1; //горизонталь
do
// ферзи уже расставлены в горизонталях 1..row-1
spotsPossible=0;
for i=l to 8 //вертикаль на горизонтали
if клетка (row, i) атакована
spotsPossible=spotsPossible+l ;
if uniform(l, spotsPossible)==l
try=i ;
end if ;
end if ;
end for;
if spotsPossible>0
result[row]=try ;
row=row+l ;
end if ;
while row<9 && spotsPossible>0 ;
return (spotsPossible>0)
end.
Посмотрим, как работает этот алгоритм. В цикле мы проходим по всем восьми горизонталям доски. Для каждой из горизонталей мы последовательно просматриваем все ее клеточки и если клетка атакована, то переменная spotsPossible увеличивается на единицу. Следующий оператор if выглядит несколько странно, но посмотрим, что происходит, если опустить первую горизонталь, на которой не атакована ни одна клетка. На первой вертикали функция uniform генерирует случайное число между 1 и 1, т. е. 1, поэтому переменная try будет указывать на первую вертикаль. Во второй вертикали uniform генерирует число между 1 и 2, которое с 50%-ной вероятностью будет единицей и с 50%-ной вероятностью двойкой, поэтому вероятность того, что новым значением переменной try станет двойка, равна 50%. В третьей вертикали uniform генерирует число между 1 и 3; это число с вероятностью 33% будет 1, и также с вероятностью 33% значение try станет равно 3. Окончательно мы заключаем, что для каждой из свободных вертикалей вероятность быть опробованной на данном проходе равна 1/spotsPossible. Затем все повторяется для остальных горизонталей. Такие действия продолжаются до тех пор пока либо значение spotsPossible не станет нулевым ввиду отсутствия неатакованных клеток, либо переменная rows не примет значение 9, поскольку все ферзи будут расставлены. В первом случае алгоритм завершает свою работу и сообщает о неудачном исходе. Во втором проблема расстановки восьми ферзей решена, и алгоритм сообщает об удачном исходе.
Полный статистический анализ алгоритма показывает, что вероятность успеха равна 0.1293, а среднее число повторений, необходимых для его достижения, около 6.971. Приведенное выше уравнение показывает, что алгоритм выполнит при этом 55 проходов. Рекурсивному же алгоритму понадобится по крайней мере вдвое больше проходов.
2.1.8. Шервудские алгоритмы
Шервудские алгоритмы всегда возвращают ответ, и этот ответ всегда правильный. Эти алгоритмы применимы в ситуациях, когда различие между наилучшим, средним и наихудшим случаями в детерминированном алгоритме очень велико. Применение случайности позволяет шервудским алгоритмам сократить спектр возможностей, подтянув наихудший и наилучший случаи к среднему.
Примером может служить поиск осевого элемента в алгоритме быстрой сортировки. При анализе этого алгоритма мы пришли к выводу, что наихудшим для него является ситуация, в которой список уже отсортирован, так как каждый раз мы будем натыкаться на минимальный элемент списка. Если же вместо выбора начального элемента мы будем выбирать случайный элемент между началом и концом, то вероятность наихудшего исхода уменьшится. Совсем избежать его нельзя — и при случайном выборе оси мы можем всякий раз натыкаться на наименьший элемент, однако вероятность такого исхода очень мала. Оборотная сторона такого подхода состоит в том, что если в списке реализовался наилучший исход для детерминированного алгоритма — первым элементом всякий раз оказывается медиана оставшейся части списка, — то маловероятно, чтобы наш случайный выбор пал именно на нее. Поэтому шансы на наилучший и наихудший исход понижаются.
Тот же самый подход можно применять и в задаче поиска. При двоичном поиске прежде, чем добраться до некоторых элементов списка, мы должны с необходимостью совершить несколько неудачных проверок. Шервудский вариант «двоичного» поиска выбирает случайный элемент между началом и концом списка и сравнивает его с искомым. Иногда оставшийся кусок оказывается меньше, чем тот, что мы бы получили при настоящем двоичном поиске, а иногда — больше. Так, например, не исключено, что в списке из 400 элементов мы выберем для пробного сравнения не 200-ый, а сотый. Если искомый элемент находится среди первых ста, то наша шервудская версия алгоритма поиска позволяет отбросить 75% списка вместо 50% в стандартном алгоритме. Однако если интересующий нас элемент больше сотого, то отброшенными окажутся лишь 25% списка. Вновь в некоторых случаях мы получаем выигрыш, а иногда проигрываем.
Как правило, шервудские алгоритмы уменьшают время обработки наихудшего случая, однако увеличивают время обработки наилучшего. Подобно Робин Гуду из Шервудского леса этот подход грабит богатых, чтобы отдать бедным.
2.2. Сравнение вероятностных алгоритмов
Подведем итоги обсуждению алгоритмов. Численные вероятностные алгоритмы всегда дают ответ, и этот ответ будет тем точнее, чем дольше они работают. Алгоритмы Монте Карло всегда дают ответ, но иногда ответ оказывается неправильным. Чем дольше выполняется алгоритм Монте Карло, тем выше вероятность того, что он даст правильный ответ. Повторный вызов алгоритма Монте Карло также приводит к улучшению результата. Алгоритмы Лас Вегаса не могут вернуть неправильного результата, но они могут и не вернуть никакого результата, если им не удалось найти правильный ответ. Шервудскую технику можно применять к любому детерминированному алгоритму. Она не влияет на правильность алгоритма, а лишь уменьшает вероятность реализации наихудшего поведения. Вероятность наилучшего поведения при этом, правда, тоже понижается.
3. ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
Ричард Беллман ввел понятие динамическое программирование для характеристики алгоритмов, действующих в зависимости от меняющейся ситуации. Ключевым в его подходе является использование полиномиальных по времени алгоритмов вместо экспоненциальных.
Динамическое программирование - метод оптимизации, приспособленный к задачам, в которых процесс принятия решений может быть разбит на отдельные этапы (шаги). Такие задачи называют многошаговыми.
Метод состоит в том, что оптимальное решение строится постепенно, шаг за шагом. На каждом шаге оптимизируется решение только этого шага, но решение выбирается с учетом последствий, так как решение, оптимальное для этого шага, может привести к неоптимальному решению всей задачи, т. е. оптимальное решение задачи содержит оптимальные решения ее подзадач.
Метод динамического программирования - один из наиболее мощных и широко известных математических методов современной теории управления, был предложен в конце 50-х годов американским математиком Р. Беллманом и быстро получил широкое распространение. Р. Беллман сформулировал принцип оптимальности:
Каково бы ни было начальное состояние на любом шаге и решение, выбранное на этом шаге, последующие решения должны выбираться оптимальными относительно состояния, к которому придет система в конце данного шага.
Использование этого принципа гарантирует, что решение, выбранное на любом шаге, является не локально лучшим, а лучшим с точки зрения задачи в целом.
Данный метод усовершенствует решение задач, решаемых, например, с помощью рекурсий или перебора вариантов.
Условия применения динамического программирования:
Небольшое число подзадач. Уменьшение числа подзадач происходит из-за многократного их повторения (т. н. перекрывающиеся подзадачи) Дискретность (неделимость) величин, рассматриваемых в задаче.3.1. Числа Фибоначчи
Главная особенность алгоритмов типа "разделяй и властвуй” заключается в том, что одни делят задачи на независимые подзадачи. Когда подзадачи независимы, ситуация усложняется, и в первую очередь потому, что непосредственная рекурсивная реализация даже простейших алгоритмов этого типа может требовать недопустимо больших затрат времени. Например, программа 10.1 представляет собой непосредственную рекурсивную реализацию рекуррентного соотношения, определяющего числа Фибоначчи. Не используйте эту программу - она исключительно неэффективна. В самом деле, количество рекурсивных вызовов для вычисления FN в точности равно FN+1. Но FN приблизительно равно фN, где ф ~ 1.618 есть золотая пропорция. Суровая правда заключается в том, что время выполнения программы, реализующей это элементарное вычисление, определяется экспоненциальной зависимостью.
Программа 10.1 Числа Фибоначчи (рекурсивная реализация)
Эта программа, хотя и выглядит компактно и изящно, неприменима на практике, поскольку время вычисления FN экспоненциально зависит от N. Время вычисления FN+1 в 1.6 раз больше времени вычисления FN. Например, поскольку ф9 > 60, если для вычисления FN компьютеру требуется около секунды, то для вычисления FN+9 потребуется более минуты, а для вычисления FN+18 - больше часа.
int F(int i) {
if (i < 1) return 0;
if (i == 1) return 1;
return F(i-l) + F(i-2); }
Эти числа возрастают экспоненциально, поэтому размер массива невелик - например, F45 = - наибольшее число Фибоначчи, которое может быть представлено 32-разрядным целым, поэтому достаточно использовать массив с 46 элементами.
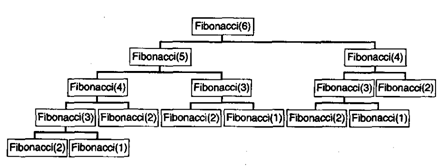
Рис. 11.1. Последовательность вызовов алгоритма Фибоначчи (6)
И напротив, можно легко вычислить первые N чисел Фибоначчи за время, пропорциональное значению N, и запомнив их в следующем массиве:
F[0] = 0; F[l] = 1;
for (i = 2; i <= N; i++)
F[i] = F[i-1] + F[i-2];
Этот подход предоставляет нам непосредственный способ получения численных решений для любых рекуррентных соотношений. В случае с числами Фибоначчи можно даже обойтись без массива и ограничиться отслеживанием только двух последних предшествующих значений; для многих других часто встречающихся рекуррентных соотношений необходимо поддерживать массив, хранящий все известные значения.
Рекуррентное соотношение - это рекурсивная функция с целочисленными значениями. Рассуждения, приведенные в предыдущем абзаце, подводят нас к выводу о том, что значение любой такой функции можно определить, вычисляя все значения этой функции, начиная с наименьшего, используя на каждом шаге ранее вычисленные значения для подсчета текущего значения. Эта технология называется восходящим динамическим программированием (bottom-up dynamic programming). Она применима к любому рекурсивному вычислению при условии, что мы можем себе позволить хранить все ранее вычисленные значения. Такая технология разработки алгоритмов успешно используется для решения широкого круга задач. Поэтому следует уделить внимание простой технологии, которая может изменить зависимость времени выполнения алгоритма с экспоненциальной на линейную!
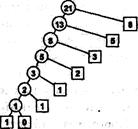
Нисходящее динамическое программирование (top-down dynamic programming) — еще более простая технология, которая позволяет автоматически выполнять рекурсивные функции при том же (или меньшем) количестве итераций, что и восходящее динамическое программирование. При этом мы вводим в данную рекурсивную программу инструментальные средства, обеспечивающие сохранение каждого вычисленного ею (в качестве заключительного действия) значения и проверку сохраненных значений во избежание повторного вычисления любого из этих значений (в качестве ее первого действия). Программу 10.2 можно рассматривать как механически измененную программу 10.1, в которой благодаря применению нисходящего динамического программирования времени выполнения становится линейным. Рисунок 10.1 фиксирует радикальное уменьшение числа рекурсивных вызовов, что достигается посредством этого простого автоматического изменения. Иногда нисходящее динамическое программирование называют также мемуаризацией (memoization).
Сохраняя вычисляемые нами значения в статическом массиве, мы явным образом исключает любые повторные вычисления. Эта программа вычисляет FN за время, пропорциональное N, что кардинально отличается от времени O(fN), которое требуется программе 10.2 для выполнения тех же вычислений.
 int F(int i)
int F(int i)
{ int t;
if (knownF[i] != 0) return knownF[i];
if (i == 0) t = 0;
if (i == 1) t = 1;
if (i > 1) t = F(i-l) + F(i-2);
return knownF[i] = t; }
Рисунок 10.2 применение нисходящего
динамического программирования
для вычисления чисел Фибоначчи
3.2. Примеры задач
3.2.1. Задача о ранце
В качестве боле сложного примера рассмотрим задачу о ранце, вор, грабящий сейф, находит в нем N видов предметов различных размеров и ценности, но имеет только небольшой ранец емкостью N, в котором может унести только часть добычи. Задача заключается в том, чтобы определить сочетание предметов, которые вор должен уложить в ранец, чтобы общая стоимость похищенного оказалась максимальной. Например, при наличии типов предметов, представленных множеством items{[3,4],[4,5],[7,10],[8,11],[9,13]}, вор, располагающий ранцем, размер которого равен 17, может взять только пять (но не шесть) предметов А общей стоимостью, равной 20, или предметы D и Е с суммарной стоимостью, равной 24, или предметы в одном из множества других сочетаний. Наша цель состоит в том, чтобы найти эффективный алгоритм для определения максимума среди всех возможностей при любом заданном наборе предметов и вместимости ранца.
Решения задачи о ранце важны для многих приложениях. Например, у транспортной компании может появиться потребность в определении наилучшего способа загрузки грузовой машины или транспортного самолета товарами, предназначенными для доставки. В подобных приложениях могут возникать и другие варианты этой задачи: например, количество элементов каждого вида может быть ограничено, или же нужно загрузить два грузовика. Многие из таких вариантов этой задачи можно решать путем применения того же подхода, который мы собираемся исследовать для решения сформулированной выше базовой задачи; другие варианты оказываются гораздо более сложными. Можно четко отделить решаемые задачи этого типа от нерешаемых.
В рекурсивном решении задачи о ранце при каждом выборе предмета мы полагаем, что можем (рекурсивно) определить оптимальный способ заполнения оставшейся емкости ранца. При размере ранца cap для каждого типа i из множества предлагаемых для выбора типов элементов мы определяем общую стоимость элементов, которые можно было бы унести, укладывая элемент типа i в ранец, при оптимальной упаковке остальных элементов. Этот оптимальный способ упаковки представляет собой просто способ упаковки, определенный (или подлежащий определению) для меньшего ранца размера cap-items[i].size. В этом решении используется следующий принцип: принятые оптимальные решения в дальнейшем не требуют пересмотра. Как только установлено, как оптимально упаковать ранцы меньших размеров, эти задачи не требуют повторного исследования, какими бы ни были следующие элементы.
Программа 10.3 есть прямое рекурсивное решение, в основу которого положены приведенные выше рассуждения. Опять-таки, эта программа неприменима для решения встречающихся на практике задач, поскольку из-за большого объема повторных вычислений на ее решение затрачивается экспоненциальное время. В то же время мы можем применить нисходящее динамическое программирование, чтобы избавиться от этой проблемы. Как и раньше, эта методика исключает все повторные вычисления
Программа 10.3 Задача о ранце (рекурсивная реализация)
В ней предполагается, что элементы являются структурами с размером и стоимостью, которые определены следующим образом:
typedef struct {int size; int val;} item;
и что в нашем распоряжении имеется массив N элементов типа item. Для каждого возможного элемента мы (рекурсивно) вычисляем максимальную стоимость, которую можно было бы получить, включив этот элемент в выборку, а затем выбираем максимальную из всех стоимостей.
int knap(int cap)
{ int i, space, max, t;
for (i = 0, max = 0; i < N; i++)
if ((space = cap-items[i].size) >= 0)
if ((t = knap(space) + items [i] .val) > max)
max = t ;
return max; }
Программа 10.4 Задача о ранце (динамическое программирование)
Эта программа, представляющая собой механически измененную программу 10.3, снижает время выполнения с экспоненциального до линейного. Мы просто сохраняем все вычисленные значения функции, а затем вместо того, чтобы выполнять рекурсивные вызовы, отыскиваем соответствующие сохраненные значения всякий раз, когда они требуются (используя сигнальные метки для представления неизвестных значений), благодаря чему мы можем отказаться от вызовов функций. Индекс элемента сохраняется, поэтому при желании всегда можно восстановить содержимое ранца после вычисления: элемент itemKnown[M] помещается в ранец, остальное содержимое совпадает с оптимальной упаковкой ранца размера M-itemKnown[M].size, следовательно, в ранце находится itemKnown [M-items[M] .size] и т. д.
int knap(int M)
{ int i, space, max, maxi = 0, t;
if (maxKnown[M] != 0) return maxKnown[M];
for (i = 0, max = 0; i < N; i++)
if ((space = M-items [i] . size) >= 0)
if ( (t = knap(space) + items [i] .val) > max)
{ max = t; maxi = i; }
maxKnown[M] = max;
itemKnown[M] = items [maxi];
return max; }
Динамическое программирование принципиально исключает все повторные вычисления в любой рекурсивной программе, при условии, что мы можем себе позволить сохранять значения функции для аргументов, которые меньше, чем текущий вызов.
Свойство. Динамическое программирование уменьшает время выполнения рекурсивной функции максимум до значения, необходимого для вычисления функции для всех аргументов, меньших или равных данному аргументу, при условии, что стоимость рекурсивного вызова остается постоянной.
Применительно к задаче о ранце, из этого свойства следует, что время выполнения алгоритма ее решения пропорционально произведению NM. Таким образом, задача о ранце легко поддается решению, когда емкость ранца не очень велика; для очень больших емкостей время и требуемый объем памяти могут оказаться недопустимо большими.
Восходящее динамическое программирование также применимо к задаче о ранце. Действительно, метод восходящего программирования можно применять во всех случаях, когда применим метод нисходящего программирования, хотя при этом необходимо быть уверенным в том, что значения функции вычисляются в соответствующем порядке, то есть, чтобы каждое значение к тому моменту, когда в нем возникает необходимость, уже было вычислено. Для функций, имеющих только один целочисленный аргумент, подобных двум рассмотренным выше, мы просто продолжаем увеличивать порядок аргумента; для более сложных рекурсивных функций определение правильного порядка может оказаться сложной задачей.
Например, мы не обязаны ограничиваться рекурсивными функциями только с одним целочисленным аргументом. При наличии функции с несколькими целочисленными аргументами решения меньших подзадач можно сохранить в многомерных массивах, по одному для каждого аргумента. В других ситуациях целочисленные аргументы вообще не требуются, вместо этого используется абстрактная формулировка дискретной задачи, позволяющую разделить задачу на подзадачи меньших размеров.
При использовании нисходящего динамического программирования известные значения сохраняются; при использовании восходящего динамического программирования они вычисляются заранее. В общем случае мы отдаем предпочтение нисходящему динамическому программированию перед восходящим, поскольку:
■ оно представляет собой механическое преобразование естественного решения задачи;
■ порядок решения подзадач определяется сам собой;
■ решение всех подзадач может не потребоваться.
Приложения, в которых применяется динамическое программирование, различаются по сущности подзадач и объему сохраняемой для них информации.
Критический момент, который мы не можем игнорировать, состоит в том, что динамическое программирование становится неэффективным, когда количество возможных значений функции, которые могут нам потребоваться, столь велико, что мы не можем себе позволить сохранять их (при нисходящем программировании) или вычислять предварительно (при восходящем программировании). Например, если в задаче о ранце величина М и размеры элементов суть 64-разрядные величины или числа с плавающей точкой, мы не сможем сохранять значения за счет использования индексов в массиве. Это несоответствие — не просто небольшое неудобство, оно создает принципиальные трудности. Для подобных задач пока не известно ни одно более-менее эффективное решение, имеются все основания полагать, что эффективного решения для них вообще не существует.
Динамическое программирование — это методика проектирования алгоритмов, которая рассчитана в первую очередь на решения сложных задач. Однако нисходящее динамическое программирование является базовой технологией разработки эффективных реализаций рекурсивных алгоритмов.
3.2.2. Задача поиска минимального маршрута
В таблице размером N*N, где N<13, клетки заполнены случайным образом цифрами от 0 до 9. Предложить Чебурашке алгоритм, позволяющий найти маршрут из клетки (1,1) в клетку (N, N) и удовлетворяющий следующим условиям:
1. любые две последовательные клетки в маршруте имеют общую сторону;
2. количество клеток маршрута минимально;
3. сумма цифр в клетках маршрута максимальна.
Будем искать наилучшие пути, идущие из клетки (1,1) во все остальные клетки таблицы, в частности и в клетку (N, N). Для этого в некоторой вспомогательной таблице B того же размера, что и А, будем отмечать суммы цифр оптимальных путей, ведущих в соответствующие клетки. Так в клетке(1,1) таблицы В окажется число А(1,1), потому что путь, ведущий в нее, состоит из одной клетки. Так же легко заполняются клетки (1,2) и (2,1) таблицы В. В них тоже ведут единственные пути и суммы цифр вдоль них равны А(1,1)+А(1,2) и А(1,1)+А(2,1) соответственно.
Поясним сказанное на конкретном примере. Пусть таблица А размером 5*5 имеет вид, представленный на рис. 9.3. Нумерация клеток идет от левого верхнего угла. Проследим за заполнением таблицы В. О клетках (1,2) и (2,1) уже говорилось. Чтобы заполнить клетку (2,2), заметим, что в нее можно попасть либо из клетки (1,2), либо из клетки (2,1). Следовательно, в клетку (2,2) таблицы В надо записать либо число В(1,2)+А(2,2), либо число В(2,1)+А(2,2), в зависимости от того, какое из них больше. Заполнение остальных клеток таблицы В аналогично.
Если путь, ведущий в эту клетку один, то в клетку вписывается сумма цифр вдоль этого пути. Такими клетками являются клетки вида (1,J) и (J,1).
Если же в клетку (I, J) можно попасть из клеток для которых подсчитаны значения В, то необходимо выбрать М=мах{B(I, J-1), B(I-1,J} и записать в клетку B(I, J) число М+А(I, J).
Клетку B(I, J) соединим чертой с той клеткой, где был достигнут максимум М. Для нахождения искомого маршрута достаточно пройти из клетки (N, N) в клетку (1,1) по черточкам.
Таб. А
4 | 3 | 5 | 7 | 5 |
1 | 9 | 4 | 1 | 3 |
2 | 3 | 5 | 1 | 2 |
1 | 3 | 1 | 2 | 0 |
4 | 6 | 7 | 2 | 1 |
Таб. В
4 | --- | 7 | --- | 12 | --- | 19 | --- | 24 |
| | | | | | ||||||
5 | 16 | --- | 20 | --- | 21 | --- | 27 | |
| | | | | | | | |||||
7 | 19 | --- | 25 | --- | 26 | --- | 29 | |
| | | | | | | | | | ||||
8 | 22 | --- | 26 | --- | 28 | --- | 29 | |
| | | | |||||||
12 | 28 | --- | 35 | --- | 37 | --- | 38 |
// Программа
int max(int a1, int a2) {
return (a1>a2)? a1:a2;
}
void main() {
int i, k,j, N;
int a[6][6]={0}, b[6][6]={0};
int c[11][2];
scanf(“%d” , &N); //ввод размера матрицы
for (i= 1; i<= N; i++) //ввод данных
for (k= 1; k<=N; k++)
scanf(“%d” , &a[i][k]);
b[1][1]=a[1][1];
for (i =2; i<=N; i++) { //заполнение первой горизонтали и вертикали
b[1][i] = a[1][i]+b[1][i-1];
b[i][1] = a[i][1]+b[i-1][1];
}
for (i = 2; i<=N; i++) //расчет остальных элементов матрицы
for (k = 2; k<= N; k++)
b[i][k]=a[i][k]+max(b[i-1][k],b[i][k-1]);
i =N; //выбор кратчайшего пути максимальной стоимости
k =N;
j =2*N-1;
c[1][1] =1;
c[1][2] =1;
while (i!=1 || k!=1) {
c[j][1] =i;
c[j][2] =k;
if (i==1)
k--;
else if (k==1)
i--;
else if (max(b[i-1][k],b[i][k-1])==b[i][k-1])
k--;
else
i--;
j--;
}
//вывод пути на экран
for (i =1; i< 2*N; i++)
printf (“%d, %d ;”,c[i][1],c[i][2]);
}
// Результат 1,1 ; 1,2 ; 2,2 ; 3,2 ; 4,2 ; 5,2 ; 5,3 ; 5,4 ; 5,5



