В первой главе дано описание нескольких, практически, важных объектов автоматизации. Вначале, в качестве объекта управления рассматривается технологический комплекс, представляющий собой взаимосвязанную систему из двух электроприводов, выполняющую функцию намотки длинномерных материалов. Получена математическая модель объекта в виде системы дифференциальных уравнений с переменными параметрами. В целях повышения показателей качества технологического процесса, необходимо решить проблему динамического проектирования регулятора, обеспечивающего взаимосвязанное функциональное управление электроприводами, параметры которых изменяются в существенных пределах. Далее, рассматриваются технологический резервуар, предназначенный для получения смеси с заданной концентрацией, и синхронная машина, совместно с турбиной. Даны описания указанных объектов в пространстве состояний. Отмечаются такие их особенности, как нестационарность и неопределенность параметров математических моделей. В конце главы приведен краткий обзор методов синтеза САУ динамическими объектами.

Во второй главе сформулирована общая постановка задачи синтеза САУ динамическими объектами, дана характеристика инженерных показателей качества систем управления, описаны основные положения принципа гарантируемой динамики, сформулирована общая методика синтеза САУ на его основе.

В работе предполагается, что объект управления описывается, в общем, случае следующим векторным дифференциальным уравнением в переменных состояния:

(1)

где 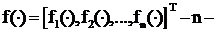мерная вектор-функция, компоненты которой, в общем случае, являются непрерывно-дифференцируемыми нелинейными функциями от своих аргументов; 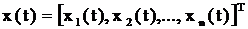– n-мерный вектор состояния объекта; – m-мерный вектор управляющих воздействий; – -мерный вектор внешних возмущающих воздействий; 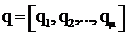− μ - мерный вектор-параметр объекта; Q – ограниченное подмножество параметров объекта; Т – знак транспонирования; х0 − начальное состояние объекта; t − текущее непрерывное время; t0, tк − моменты начала и окончания процесса управления.

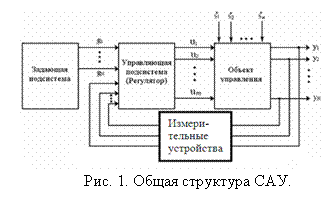
Как известно, система автоматического управления (рис.1) состоит из объекта управления и управляющей подсистемы (регулятора), основная функция которой состоит в поддержании компонентов вектора управляемых переменных y(t)=[y1(t), y2(t),.., yN(t)] в соответствии с желаемой программой движения g(t), при наличии возмущающих воздействий, определяемых вектором возмущений .

Регулятор осуществляет реализацию алгоритма (закона) управления u(t) на основе вектора ошибки управления e(t):

.

Функциональная связь между векторами управляемых переменных y(t) и состояния x(t) объекта управления определяется формулой:

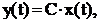(2)

Подпись: Рис. 1. Общая структура САУ. где - заданная вещественная матрица размерности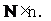

Предполагается, что заданы следующие исходные данные:

·  математическая модель объекта управления в пространстве состояний (1) и вектор выхода y(t) проектируемой САУ.

·  алгоритм функционирования САУ, т. е. цель управления в виде вектора задания g(t).

·  инженерные требования к качеству проектируемой САУ в форме векторов где - значения времен регулирования, допустимых максимальных динамических и статических ошибок управления соответственно по каждой управляемой переменной yi(t).

Задача синтеза регулятора САУ формулируется следующим образом. На основе указанных выше исходных данных, необходимо определить структуру и параметры закона управления u(t) для динамического объекта (1), обеспечивающие устойчивость замкнутой системы и заданные инженерные показатели качества проектируемой САУ.

Решение сформулированной задачи, далее, осуществляется в условиях полной и неполной информации об управляемом объекте. В случае полной информации, считается, что вектор-параметр объекта q задается точно а компоненты вектора возмущений ξ(t) являются детерминированными, т. е. известными функциями. В случае, если вектор-параметр q точно неизвестен, а имеет параметрическую неопределенность, задача синтеза регулятора решается в условиях неопределенности.

При этом можно выделить следующие задачи:

1)  задача параметрического синтеза регулятора;

2)  задача структурного синтеза регулятора.

В первом случае структура закона управления задается. В частности, если регулятор строится с использованием линейных обратных связей, закон управления имеет вид:

,

где 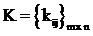- матрица искомого регулятора.

Во втором случае структура и параметры искомого закон управления определяются одновременно в процессе синтеза регулятора САУ.

Рассматриваются вопросы, связанные с использованием в задачах синтеза САУ известных критериев: интегральные показатели качества; критерий допустимого качества проф. . В работе, для динамического проектирования регуляторов САУ, используются критерий допустимого качества и принцип гарантируемой динамики.

Вначале, рассматривается проблема построения некоторой динамической системы (S), обладающей заданными динамическими свойствами и функционирующей в интервале 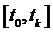. Предполагается, что общая эффективность этой системы определяется вектор-функцией 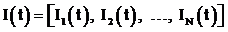, где Ii(t) – скалярные оценочные функции, определяющие качество отдельных подсистем или их функций. Пусть задача состоит в определении структуры и (или) параметров системы, обеспечивающих выполнение критериальных условий:

(3)

где - положительные функции, задающие верхние и нижние границы соответствующих допустимых областей для оценочных функций :

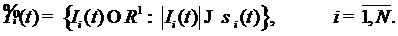
Таким образом, сформулированная цель достигается, если выбрать структуру и вектор-параметр рассматриваемой системы S так, чтобы компоненты вектора принадлежали соответствующим подмножествам , т. е. 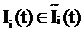. Можно отметить, что многие важные прикладные задачи выбора решений в различных областях техники (автоматики, радиотехники, мехатроники и др.) можно свести к такой постановке. Математические условия, выполнение которых обеспечивает достижение заданных критериальных ограничений (3), получены в рамках принципа гарантируемой динамики, и определяются следующей теоремой.

Теорема 1. Пусть Тогда, для того, чтобы при оценочные функции удовлетворяли условиям (3), достаточно выполнения функциональных соотношений

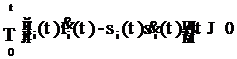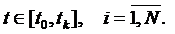, (4)

Таким образом, обеспечивая выполнение функциональных неравенств (4), можно гарантированным образом достичь принадлежность оценочных функций заданным допустимым областям , т. е. . При этом, описание подмножеств дается следующими соотношениями:

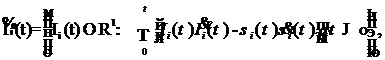
(5)

Критериальные условия (4) являются основными функциональными соотношениями принципа гарантируемой динамики.

Далее, для того, чтобы использовать соотношения (4) для синтеза САУ многомерными технологическими объектами принимается, что оценочные функции определяются компонентами вектора ошибки управления :

Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6