![]()
Тогда критериальные условия (4) принимают следующий вид:
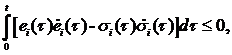
![]() (6)
(6)
Структура соотношений (6) такова, что в нее одновременно входят желаемые состояния (задающие воздействия) ![]() и скорости изменения компонентов вектора ошибки управления
и скорости изменения компонентов вектора ошибки управления ![]() , а также инженерные требования к качеству регулирования, определяемые положительными функциями
, а также инженерные требования к качеству регулирования, определяемые положительными функциями ![]() Следовательно, эти условия устанавливают связи между желаемым состоянием объекта управления, его динамическими свойствами и требуемыми инженерными показателями качества проектируемой САУ, что дает возможность использовать их для построения методов и алгоритмов синтеза САУ многомерными динамическими объектами.
Следовательно, эти условия устанавливают связи между желаемым состоянием объекта управления, его динамическими свойствами и требуемыми инженерными показателями качества проектируемой САУ, что дает возможность использовать их для построения методов и алгоритмов синтеза САУ многомерными динамическими объектами.
Описание допустимых подмножеств ![]() для переходных процессов ei(t) определяется следующими соотношениями:
для переходных процессов ei(t) определяется следующими соотношениями:
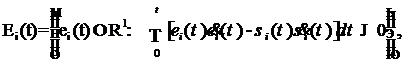
![]()
Таким образом, выполнение функциональных неравенств (6) гарантированным образом обеспечивает принадлежность ошибок управления ei(t) заданным допустимым областям![]() , т. е.
, т. е. ![]() .
.
На основе критериальных условий (6) разработана общая методология синтеза регуляторов САУ многомерными технологическими объектами в виде обобщенного алгоритма.
В третьей главе рассматривается применение принципа гарантируемой динамики для синтеза регуляторов САУ и идентификации состояний многомерных САУ.
В начале, рассматривается многомерный объект управления, динамика которого описывается векторным уравнением в отклонениях (e(t)=x(t)):
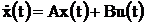 ,
, 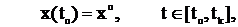 (7)
(7)
где![]() ,
, ![]() ;
; ![]() - состояние объекта в начальный момент времени
- состояние объекта в начальный момент времени ![]() ;
; ![]() - конечный момент управления.
- конечный момент управления.
Далее, предполагается, что:
1) объект (7) обладает свойством управляемости;
2) компоненты вектора состояния x(t) доступны для измерения;
3) задана структура регулятора, определяемая уравнением вида
![]()
где  матрица обратной связи (регулятора);
матрица обратной связи (регулятора);
4) заданы ограничения на компоненты вектора управления u(t) :
![]() (8)
(8)
где ![]() – максимально допустимое значение управляющей переменный
– максимально допустимое значение управляющей переменный ![]() .
.
Допустимое подмножество ![]() для вектора
для вектора ![]() определяется соотношением
определяется соотношением
![]()
где допустимые области
![]()
5) элементы матрицы А объекта управления имеют интервальную неопределенность, т. е.
![]() ,
,
где 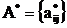 матрица объекта, размерностью
матрица объекта, размерностью ![]() составленная из номинальных значений
составленная из номинальных значений ![]() элементов матриц
элементов матриц ![]() ;
; ![]() – матрица, характеризующая неопределенности в задании объекта управления. Считается, что интервалы неопределенностей для матрицы A известны:
– матрица, характеризующая неопределенности в задании объекта управления. Считается, что интервалы неопределенностей для матрицы A известны:
![]() ,
,
где ![]() - положительные числа, определяющие границы изменения параметрических возмущений
- положительные числа, определяющие границы изменения параметрических возмущений ![]() .
.
Качество проектируемой САУ оценивается следующими критериальными соотношениями:
![]() , (9)
, (9)
где ![]() – положительные функции, которые задают максимально допустимые отклонения
– положительные функции, которые задают максимально допустимые отклонения ![]() в переходном процессе. Следует отметить, что выбор
в переходном процессе. Следует отметить, что выбор ![]() осуществляется по первичным (инженерным) требованиям к точности и быстродействию проектируемой системы.
осуществляется по первичным (инженерным) требованиям к точности и быстродействию проектируемой системы.
Допустимая область ![]() для
для ![]() определяется выражением
определяется выражением
![]()
Тогда, допустимое подмножество ![]() для вектора
для вектора ![]() задается соотношением
задается соотношением
![]()
В рассмотрение вводится вектор-параметр регулятора 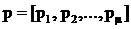 размерности
размерности ![]() , составленный из строк матрицы K. Для вектор-параметра
, составленный из строк матрицы K. Для вектор-параметра ![]() , на основе условий (8) и (9), определим следующие подмножества:
, на основе условий (8) и (9), определим следующие подмножества:
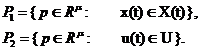
Задача синтеза регулятора заданной структуры, в условиях параметрической неопределенности в описании объекта, формулируется следующим образом. Найти вектор-параметр p регулятора, принадлежащий пересечению подмножеств ![]() и
и ![]() , т. е.
, т. е. ![]() . При этом заданные требования (8) и (9) к проектируемой САУ будут удовлетворяться.
. При этом заданные требования (8) и (9) к проектируемой САУ будут удовлетворяться.
Для математического описания подмножеств ![]() и
и ![]() использованы функциональные соотношения (4) и (6) принципа гарантируемой динамики. При этом, показано, что подмножества P1 и P2 описываются следующими соотношениями:
использованы функциональные соотношения (4) и (6) принципа гарантируемой динамики. При этом, показано, что подмножества P1 и P2 описываются следующими соотношениями:
![]()
![]() ,
,
где 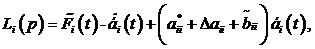
![]() .
.
![]()
![]() ,
,
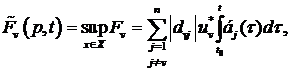
![]() ,
,
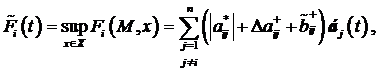
![]()
Анализ подмножеств P1 и P2 и выбор вектор-параметра ![]() можно осуществить на основе известных методов.
можно осуществить на основе известных методов.
Далее, рассматривается нестационарный линейный многомерный управляемый объект, математическая модель которого задана в отклонениях (x(t)=e(t)) в пространстве состояний:
![]() (10)
(10)
где вещественные матрицы 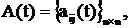
![]()
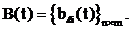
Предполагается, что объект обладает свойством управляемости, а компоненты вектора состояния x(t) измеряются.
Проблема состоит в синтезе автоматического регулятора, обеспечивающего проектируемой системе управления заданные динамические свойства, т. е. устойчивость замкнутой САУ и требуемые показатели качества системы по точности и быстродействию.
Для решения сформулированной задачи синтеза используется следующая теорема.
Теорема 2. Пусть 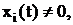
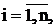 и для каждого t0 и t > t0 выполняются условия
и для каждого t0 и t > t0 выполняются условия
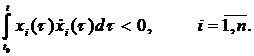 (11)
(11)
Тогда, модули невязок ![]() c течением времени убывают и
c течением времени убывают и
![]()
![]()
В целях использования соотношений (11) для синтеза искомого регулятора, введем следующие критериальные функции

|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 |





