Знак "минус" показывает, что α2 отсчитывается от диаметральной плоскости в противоположную сторону по сравнению с углом α1. Численные значения этих углов равны: α2 = α1. Можно найти угол γ, характеризующий направление силы D λH относительно магнитного меридиана. По рис. 3.3, с учетом того, что | α2 | =| α1 |, находим: γ = 360° - 2α1 = 360° - 2(360° - k) = 2k.

Следовательно, направление силы D λН зависит от магнитного курса судна k и определяется его удвоенным значением 2k.

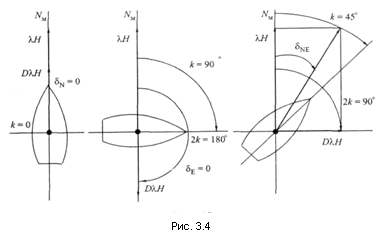
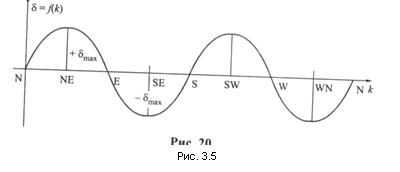
На рис. 3.4 показаны направления силы D λН на курсах 0°, 45° и 90°. Анализируя эти рисунки, можно сделать вывод: девиация от силы D λН на главных румбах (N, E, S, W) равна нулю, а на промежуточных (четвертных) курсах (NE, SE, SW, NW) равна некоторому максимальному значению δmax. Зависимость девиации от курса судна можно представить в виде графика (рис. 3.5), на котором есть четыре максимальных значения девиации и четыре нулевых. Такая девиация называется четвертной. Следует отметить, что максимальное значение четвертной девиации δmax равно коэффициенту четвертной девиации D. Его можно выражать или в градусах, или в отвлеченной мере — в радианах.

Сила Е λН. Векторное представление силы Е λН можно видеть на рис. 3.6. Вектор F3 = Е λН образуется геометрическим суммированием продольной силы и поперечной силы . Направление силы Е λН можно характеризовать углом α3 относительно поперечной судовой оси у. На рис. 3.6, кроме силы Е λН, также показана сила D λН, направление которой, как уже нам известно, определяется углом α2 относительно продольной судовой оси х. Из соотношений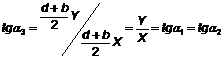

видно, что угол α3 равен углу α2. Но так как углы α3 и α2 отсчитываются от взаимноперпендикулярных осей у и х, то очевидно, что сила Е λН всегда перпендикулярна силе D λН. Следовательно, относительно магнитного меридиана сила Е λН имеет направление 2k + 90°.

Рассматривая действие силы Е λН совместно с направляющей силой λН на различных курсах судна, можно убедиться, что на четвертных магнитных курсах (NE, SE, SW, NW) эта сила не вызывает девиации, а на главных курсах (N, E, S, W), наоборот, создает максимальную девиацию. Девиация от силы Е λН, так же как и от силы D λН, носит четвертной характер. Следует отметить, что на транспортных судах величина коэффициента Е очень мала, и девиация от силы Е λН составляет доли градуса.

Рис 3.6

Сила А λН. Эта сила представляет собой геометрическую сумму двух векторов — отрицательного продольного и положительного поперечного (рис. 3.7).

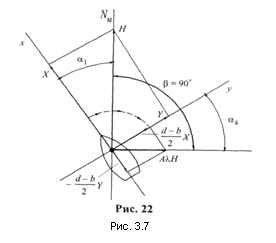
Направление силы А λН можно характеризовать углом α4, отсчитываемого от оси у, причем α4=α1 так как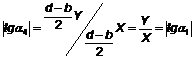

Углы α1 и α4, равные между собой, отсчитываются от взаимноперпендикулярных осей х и у, поэтому угол β, определяющий направление силы А λН в навигационном варианте, т. е. относительно магнитного меридиана, всегда равен 90°, независимо от курса судна. Это наглядно показано на рис. 3.7. Таким образом, сила А λН всегда перпендикулярна магнитному меридиану. Она создает некоторую постоянную девиацию, одинаковую на всех курсах судна. Величина девиации от силы А λН, как правило, не превышает одного градуса. Эту девиацию не уничтожают, а учитывают как часть общей поправки компаса.

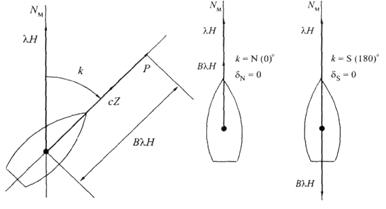
Сила В λН. Эта сила образована как алгебраическая сумма двух продольных составляющих: cZ и Р (рис. 3.8).

Значит, сила В λН — продольная, действует всегда по продольной оси х, а направление силы В λН совпадает с линией курса и характеризуется углом k. На двух курсах N и S действие силы BλН совпадает с направлением магнитного меридиана, и, следовательно, на этих курсах девиация от силы BλН равна нулю (рис. 3.9).

На курсах Е и W величина девиации от силы BλН максимальна (рис. 3.10).

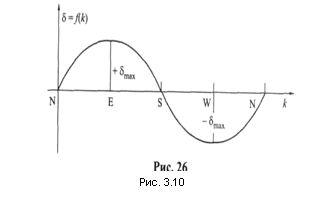Девиация, меняющая два раза знак за полный цикл изменения курса судна (360°), называется полукруговой девиацией. График полукруговой девиации от силы B λН в зависимости от курса судна показан на рис. 3.11.

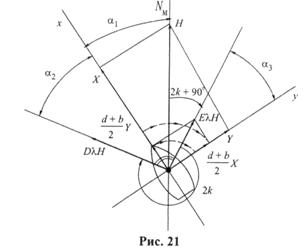
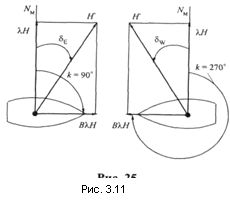
На примере силы B λН удобно рассматривать сущность коэффициентов девиации. На рис. 27 показана ситуация, когда сила B λН создает максимальную девиацию δmax. В этом случае максимальная девиация δmax наблюдается не на магнитном курсе k = 90°, а на компасном курсе k' = k - δmax = 90°. Результирующий вектор 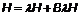определяет направление компасного меридиана NK и величину девиации δmax. Из прямоугольного треугольника следует:

(3.7)

т. e. коэффициент полукруговой девиации есть отвлеченное число, равное синусу максимальной девиации от силы B λН, наблюдаемой на компасном курсе k = 90°. При малых (остаточных) девиациях (δmax < 5°), т. е. когда судовая сила B λН компенсирована магнитами-уничтожителями, вместо выражения (3.5) можно применять приближенную формулу

δmax В (3.8)

В этом случае коэффициент В можно выражать или отвлеченно, в радианах, или в градусах. Именно в этом состоит сущность коэффициента полукруговой девиации В, и также любого другого коэффициента (D, Е, А, С), величина которого численно равна максимальной девиации (от соответствующей силы), выраженной в градусах или радианах.

Сила С λН. Эта сила получается в результате алгебраического суммирования двух поперечных составляющих: С λН =fZ + Q (рис. 3.12). Следовательно, сила С λН — поперечная, действует всегда по судовой оси y, а направление силы С λН характеризуется углом k + 90°. Сила С λН, так же как и сила B λН, создает полукруговую девиацию с двумя максимумами (на курсах N и S) и двумя нулевыми значениями (на курсах Е и W).

Основные сведения о силах, действующих на компас, и девиациях, возникающих от их влияния, представлены в табл. 3.1.

Теперь все направления магнитных сил известны в судовой системе координат, что значительно облегчает задачу их компенсации.

4 Основные принципы определения и уничтожения девиации

4.1 Точная и основная формула девиации

Геометрическая сумма сил, входящих в уравнения Пуассона с уравненными коэффициентами является направляющей силой Н' магнитной стрелки в компасном меридиане:

X'+Y'=H'=λH + A'λH +B'λH +CλH +D'λH +E'λH (4.1)

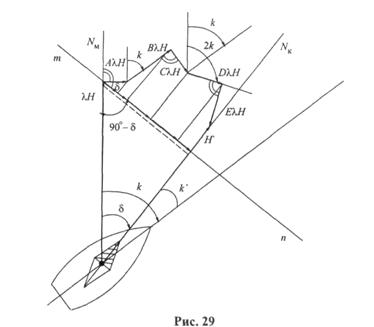
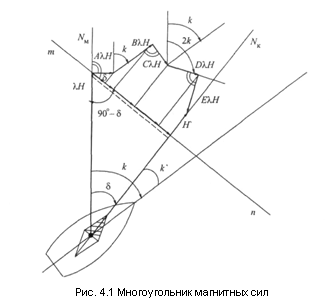
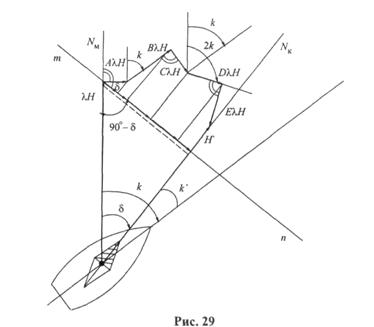
Зная величину коэффициентов и вектора Н, по формуле (4.1) можно рассчитать шесть сил и найти девиацию для любого компасного курса. Однако этот способ очень сложный. Удобнее девиацию для любого компаса получить аналитически. Для вывода такой зависимости спроецируем силы уравнения на направление перпендикулярное компасному меридиану (рис.4.1). Спроецировав и сложив все силы, получим выражение

(4.2)

Приведённая формула (4.2) является точной формулой девиации, представляющей аналитическую зависимость между коэффициентами девиации, компасным курсом судна и девиацией. Эта формула для вычисления девиации неудобна, так как искомая девиация входит в левую, и в правую части уравнения. Это уравнение можно упростить, считая девиацию малым углом. Тогда применяя следующие допущения, связанные с тригонометрическими функциями малых углов:

sin δ ≈ δ; cos ≈ 1; 2K +δ ≈ 2K.

Тогда получим

(4.3)

основную формулу девиации. В ней коэффициенты А, В, С, В, Е являются приближенными коэффициентами девиации. Данная формула может использоваться при девиации, не превышающей приблизительно 13º. В действительности она редко превышает это значение. Другим достоинством данного уравнения является то, что девиация и ее коэффициенты выражены в градусах.

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8 9 10 11 12