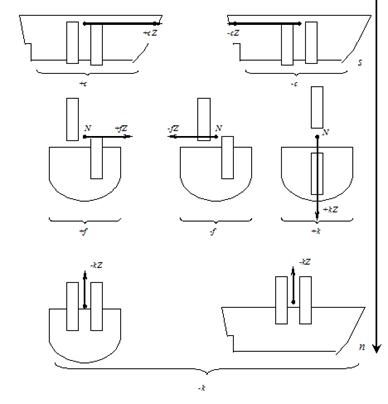
Брускам, образующим параметр c, соответствуют на судне дымовые трубы, мачты, пиллерсы и т. п.
Судового железа, образующего параметр f у компасов, расположенных в ДП судна, мало; поэтому для этих компасов параметр f близок к нулю, а для главных компасов его можно принимать равным нулю.
Брускам, образующим положительный параметр k, соответствуют на судне палубы надстроек и рубок, пиллерсы под компасом и т. п. Брускам, образующим отрицательный параметр k, соответствуют на судне стенки рубок.
Таким образом, мы получили параметры b, d, f и h близкие к нулю, следовательно в уравнениях (2.1) силы bY, dX, fZ и hY для главных компасов можно принимать равными нулю, так как главные компасы всегда устанавливаются в ДП судна и достаточно удалены от судового железа, характеризующего эти параметры.
Представляя действие отдельных частей корпуса судна в виде брусков мягкого железа, можно предугадать, какие параметры образует рассматриваемая часть корпуса судна.
Знание же параметров дает возможность судить о характере девиации, производимой рассматриваемой частью корпуса судна.
Параметры и силы (bY, dX, fZ, hY), стоящие в вершинах своеобразного ромба, и дополнительно сила gX, как правило, очень малы и ими можно пренебрегать. Наибольшие по величине параметры а, е, k располагаются по диагонали.
|
3 Преобразование уравнений Пуассона
Для практического использования удобнее иметь и рассматривать те магнитные силы, модули которых являются постоянными величинами, не зависящими от курса судна. Такие силы можно получить путем математического преобразования уравнений Пуассона.
Преобразованию подвергаются только первые два уравнения, характеризующие горизонтальные силы при прямом положении судна, без крена и дифферента.
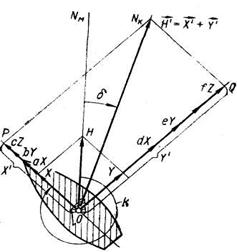
Допустим, что судно стоит на ровном киле (рис. 3.1), тогда преобразуем только первые два уравнения системы (2.2):
Х'=Х + аХ+bY+сZ+Р;
Y'= Y+dX+eY+fZ+Q. (3.1)
Если геометрически сложить первые два члена правых частей уравнений системы (3.1), получим вектор горизонтальной составляющей магнитного ноля Земли (рис. 3.1)
H = X +Y. (3.2)
Направление вектора Н относительно оси х судна определяется из выражения
tg α = Х / У. (3.3)
Горизонтальная составляющая, не зависит от изменений курса судном, так как составляющие X и Y являются её проекциями на судовые оси х и у. Аналогично можно сложить и силы, возникающие от намагничивания мягкого железа, в состав которых входят множители Х и Y.
В общем случае коэффициенты не равны, то есть а≠е и b≠d. Однако их можно уравнять посредством очевидных тождеств:
α =![]() ; b =
; b = ![]() ;
;
d = ![]() ; e =
; e = ![]() .
.
Подставим значения уравненных коэффициентов в уравнения (3.3) и получим уравнения Пуассона с уравненными коэффициентами для данной магнитной широты:
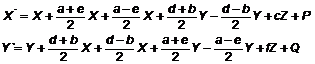 . (3.6)
. (3.6)
Геометрически сложив силы ![]() и
и ![]() и учтя, что параметры а и е отрицательны, получим равнодействующую
и учтя, что параметры а и е отрицательны, получим равнодействующую 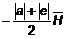 . Направление её относительно оси X судна найдём по формуле:
. Направление её относительно оси X судна найдём по формуле: ![]()
Направление этой силы противоположно направлению силы H. Значит, в плоскости магнитного меридиана действуют две силы: Н и 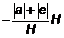 . Алгебраически сложив эти силы, получим:
. Алгебраически сложив эти силы, получим: ![]() .
.
Множитель 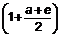 принято обозначать λ, тогда получим, что в плоскости магнитного меридиана на судне действует сила λН.
принято обозначать λ, тогда получим, что в плоскости магнитного меридиана на судне действует сила λН.
Так как параметры а и е значительно меньше единицы, то коэффициент λ всегда меньше единицы и отрицательным быть не может. Он характеризует изменение горизонтально составляющей Н земного магнетизма под влиянием мягкого железа судна. Величина его не зависит от курса судна и от магнитной широты, а зависит от расположения компаса относительно мягкого железа. Сила λН девиации не производит и является полезной силой, так как удерживает магнитную стрелку в магнитном меридиане на судне. Она всегда меньше направляющей силы Н на берегу. Как правило, на верхнем мостике (главный компас) λ = 0,8 - 0,9.
|
Аналогично, геометрически сложив силы:
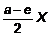 +
+ ![]() ;
; ![]() +
+ ![]() ;
; ![]() +
+ ![]()
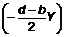 ;
;
cZ + P; fZ + Q,
получим силы D'λН, Е'λH, А'λН, В'λН и С'λН соответственно. Горизонтальные силы действуют на компасную стрелку в прямом положении судна по различным, но вполне определённым направлениям. При этом величины этих сил не зависят от курса судна и постоянны в данной магнитной широте. Данные об этих силах сведём в табл. 3.1.
Таблица 3.1
Сила | Коэффициент | Вид создаваемой девиации, δ | Величина | ||
Происхождение от влияния судового железа | Обозначение | Направление | |||
Продольного и поперечного мягкого | λH | 0° |
| - | 0,75÷0,95 |
AλH | 90° |
| Постоянная | 0,005÷0,01 | |
Твёрдого и вертикального мягкого | BλH | K |
| Полукруговая | 0,18÷0,25 |
CλH | K+90° |
| 0,12÷0,18 | ||
Продольного и поперечного мягкого | DλH | 2K |
| Четвертная | 0,06÷0,12 |
ЕλН | 2K+90° |
| 0,005÷0,01 |
Рассмотрим каждую силу в отдельности, определим направления сил (в зависимости от курса судна) и виды девиаций, создаваемых этими силами.
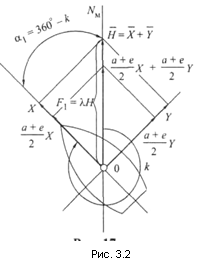
Сила λН. Вектор силы λН (рис. 3.2) представляет собой сумму двух векторов, имеющих одно и то же направление — по магнитному меридиану NM:
![]()
![]()
На рис. 3.2 через k обозначен магнитный курс судна, а через α1 — его дополнение до 360°; α1 = 360° - k.
Множитель λ — это безразмерный коэффициент, показывающий, насколько направляющая сила λН (на судне) уменьшена влиянием судового железа по сравнению с аналогичной силой Н вне судна.
Поскольку судовые параметры а и е всегда отрицательны, коэффициент λ на судах всегда меньше единицы:
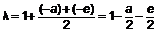 < 1
< 1
Следует отметить, что на верхнем мостике судна величина λ примерно равна 0,8 – 0,9, а в рулевой рубке λ = 0,5 – 0,7. В румпельном отделении судовое железо еще сильнее экранирует естественное магнитное поле Земли, там коэффициент λ = 0,5 – 0,3, и магнитный компас работает менее надежно, чем на открытой палубе.
Сила D λН. Векторное представление этой силы показано на рис. 3.3.
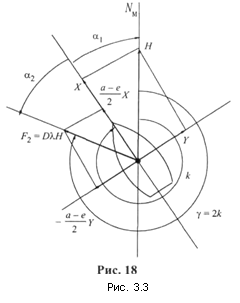
Вектор F2 = D λН образуется геометрическим сложением положительного продольного вектора ![]() , направленного к носу судна, и отрицательного поперечного вектора
, направленного к носу судна, и отрицательного поперечного вектора 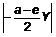 , имеющего направление к левому борту. Вектор F2 относительно диаметральной плоскости направлен под углом α2, причем
, имеющего направление к левому борту. Вектор F2 относительно диаметральной плоскости направлен под углом α2, причем 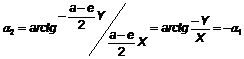

|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 10 11 12 |




