Тема исследовательской работы: « Магические квадраты» (стр. 7 )

1 Ломаной называется диагональ, которая, дойдя до края квадрата, продолжается параллельно первому отрезку от противоположного края, такую диагональ образуют заштрихованные клетки.

Глава 3. Латинские квадраты и их применение

Латинским квадратом называется квадрат n*n клеток, в которых написаны числа от 1, до n, притом так, что в каждой строке и каждом столбце встречаются все эти числа по одному разу. На рис.6 изображены два таких квадрата3*3. Они обладают интересной особенностью: если один квадрат наложить на другой, то все пары получившихся чисел оказываются различными (рис.6). Такие пары латинских квадратов называются ортогональными.

Рис.6

Впервые задачу отыскания ортогональных латинских квадратов поставил Л. Эйлер, причём в такой занимательной формулировке: «Среди 36 офицеров поровну уланов, драгунов, гусаров, кирасиров, кавалергардов и гренадеров и, кроме того, поровну генералов, полковников, майоров, капитанов, поручиков и подпоручиков, причем каждый род войск представлен офицерами всех шести рангов. Можно ли выстроить всех офицеров в каре 6 * 6 так, чтобы в любой колонне и любой шеренге встречались офицеры всех рангов?»

Эйлер не смог найти решения этой задачи. В 1901 г. было доказано, что ортогональных квадратов 6*6 не существует. В 1959 г. с помощью ЭВМ были найдены сначала ортогональные квадраты 10*10, потом 14*14, 18 *18, 22 *22. А затем было показано, что для любого n , кроме 6, существуют ортогональные квадраты n *n.

Применение магических и латинских квадратов

1. Шифрование текстов

Шифруемый текст вписывали в магические квадраты нужного размера в соответствии с нумерацией их клеток. Если затем выписать содержимое такой таблицы по строкам, то получится шифртекст, сформированный благодаря перестановке букв исходного сообщения. Рис.7

Пример магического квадрата и его заполнения сообщением показан на рисунке 7.

ПРИЛЕТАЮ ВОСЬМОГО

Шифртекст, получаемый при считывании содержимого правой таблицы по строкам, имеет вид: ОИРМ ЕОСЮ ВТАЬ ЛГОП.

2. Агротехника

Пусть требуется испытать 4 сорта пшеницы на урожайность в данной местности, причем нужно учесть влияние степени разреженности посевов и влияние двух видов удобрений. Для этого разобьем квадратный участок земли на 16 делянок. Первый сорт пшеницы посадили на делянках, соответствующих нижней горизонтальной полосе, следующий сорт - на четырех делянках, соответствующих следующей полосе, и т. д. (на рис. сорт обозначен цветом). При этом максимальная густота посевов будет на тех делянках, которые соответствуют левому вертикальному столбцу рисунка (на рис. этому соответствует уменьшение интенсивности цвета). Цифры, стоящие в клетках рисунка, пусть означают: первая - количество килограммов удобрения первого вида, вносимого на участок, а вторая - количество вносимого удобрения второго вида. Эти числа на 1 меньше чисел в ортогональных латинских квадратах. Заметим, что реализованы все возможные пары сочетаний как сорта и густоты посева, так и других компонентов: сорта и удобрений первого вида, удобрений первого и второго видов, густоты и удобрений второго вида.

Использование ортогональных латинских квадратов помогает учесть все возможные варианты в экспериментах в сельском хозяйстве, физике, химии, технике.

Глава 4. Судоку и Какуро

4.1. Феномен Судоку

Судоку (яп. 数独, дословно означает «числа - рядом») — это головоломка - пазл с числами, ставшая в последнее время очень популярной. Судоку активно публикуют газеты и журналы разных стран мира, сборники судоку издаются большими тиражами. Решение судоку - популярный вид досуга. Судоку - головоломка, получившая огромную популярность совсем недавно. Эта головоломка появилась в американских журналах в конце 70-х годов, в 80-х прижилась в Японии, где получила большое распространение. В 2004 судоку начали печатать английские газеты, откуда судоку - мания перекинулась на Европу и в Австралию. Наконец, в 2005 эта головоломка триумфально вернулась в США, завершив свой "кругосветный тур". В настоящее время издается множество специализированных журналов и сборников, книг и руководств по их решению, многие газеты печатают судоку наряду с кроссвордами и задачами по шахматам и бриджу.

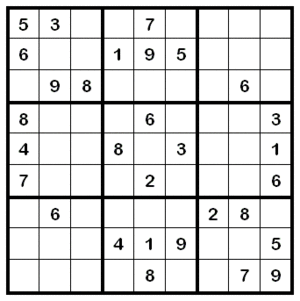
Так выглядит судоку.

Ее правила предельно просты: дан квадрат из 81 клетки, который в свою очередь состоит из 9 квадратов по 9 клеток. Нужно расставить в клетках числа от 1 до 9 так, чтобы в каждой строке и столбце большого квадрата, а также внутри каждого из малых квадратов 3х3 числа не повторялись. Часть клеток в начале заполнена, остальное нужно заполнить самостоятельно, используя логику и трезвый расчет.

В последнее время появились и более сложные модификации, чем 9 на 9 клеток. Существуют судоку с размерами 15×15 или даже 16×16, предназначенные для опытных игроков. Кроме того, есть судоку, в которых не указываются отдельные цифры, а только суммы цифр в группах клеток; то есть, само поле разбивается на прямоугольные блоки разных размеров и указывается сумма цифр входящих в каждый блок. Для детей используются судоку меньших размеров, например, 2 на 2.

Прообраз судоку впервые встречается под именем «Carré latin» («римский квадрат») и был изобретен швейцарским математиком Леонардом Эйлером в 18 веке. Этот квадрат не был разделен на 9 меньших квадратов. Настоящую популярность завоевала судоку (Sūdoku) только в наше время, когда японский журнал Nikoli начал регулярно публиковать на своих страницах эту головоломку. Тогда же она и получила своё сегодняшнее обозначение. С 2005 британская газета «Таймс» стала печатать судоку и прославила её по всей Европе. Сегодня судоку — это обязательный компонент многих газет. Среди них много изданий с многомиллионными тиражами, например, немецкая газета «Цайт» (Die Zeit), австрийский «Стандарт» (Standard). Также публикуют судоку российская газета «Труд» и журнал «Всё ясно».

Количество возможных комбинаций в судоку 9×9 составляет по расчётам Бертхама Фельгенхауэра (англ. Bertram Felgenhauer) 6 670 903 752 021 072 936 960.

Для решения судоку рекомендуется использовать карандаш, поскольку, карандаш можно легко стереть в случае ошибки. Практика решения головоломки приходит постепенно.

Лучший способ решения — записывать числа-кандидаты в вершине левого угла ячейки. После этого можно увидеть именно те числа, которые должны занимать данную ячейку. Играть в судоку нужно медленно, так как это расслабляющая игра. Некоторые головоломки можно решить за несколько минут, но на другие можно потратить часы или, в отдельных случаях, даже дни. Правильно составленная головоломка имеет единственное решение.

Будьте последовательны. Проверяйте ваши действия время от времени. Ошибка в начале может привести к неверному решению всей игры. Если Вы не находите правильного решения, попробуйте решить судоку позже. Иногда решение появляется внезапно, словно озарение.

Сначала смотрите на ряды, столбцы, и блоки 3×3 с наиболее заполненными квадратами: легче решить там, где выбор меньше. При заполнении ячейки, нужно проверить столбец, ряд и блок 3×3. Удостоверьтесь, что все другие 8 чисел, не дублируются. Легче избежать ошибок в начале игры, чем когда в решенной загадке обнаружится противоречие. Если колонка и ряд имеют одну незаполненную ячейку, то заполняйте ее. При заполнении рядов и столбцов, исключите числа, которые уже вписаны.

Когда в судоку несколько открытых ячеек в блоке 3×3 и только одна ячейка подходит для данного числа, то именно это число нужно записать в данную ячейку. Перед заполнением удостоверитесь, что число, которое Вы вписываете в ячейку, не будет встречаться в другой ячейке по столбцу, строке и в блоке 3×3.

Когда три ячейки имеют числа-кандидаты {12, 12, 13}, то число для третьей ячейки должно быть 3. Потому что, если бы это было число 1, то в одной из первых двух ячеек было бы число 2, а в другой не было бы ничего.

Имеются две стратегии, используемые для увеличения скорости решения головоломки. Выберите число, которое было найдено для большинства строк, столбцов или блоков 3×3 в судоку. Для каждого блока 3×3, который не содержит это число, ищутся другие блоки 3×3 в том же самом ряде и столбце блоков 3×3, которые содержат это «наиболее решенное число» и в решаемом блоке, исключаются места, где это число, не может быть вписано в ячейку. Таким образом, найдется единственная ячейка для этого числа.

Пример:

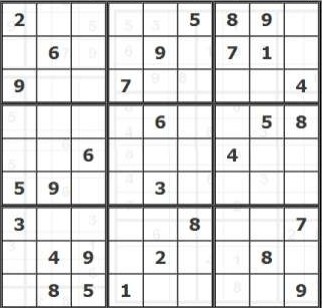
Число 9 встречается шесть раз в 6 блоках 3×3. Таким образом, число 9 можно смело ставить в центральном нижнем блоке 3×3 в верхнем левом углу, а также во втором сверху правом блоке 3×3 в первой ячейке первого ряда. В центральном блоке 3×3 число 9 может стоять только в третьей ячейке второго ряда.

Пример:

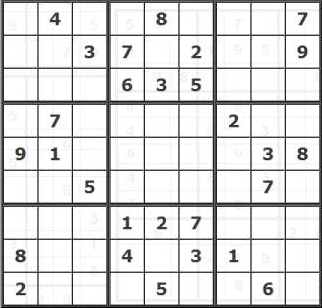
Середина верхнего ряда блоков 3×3 и середина нижнего ряда блоков 3х3 почти полностью заполнены. В середине верхнего блока три нерешенных числа — 1, 4, и 9. Анализируя такую ситуацию, можно вписать число 4 в центр блока, число 1 в правый верхний угол, а число 9 — в левый верхний угол. Аналогично можно поступить в нижним центральным блоком 3×3: в нем отсутствуют числа 6, 8 и 9. Ячейки заполняются последовательно: число 6 ставим в центр, число 9 в нижний правый угол, а число 8 в нижний левый угол.

Устройте своему мозгу настоящее испытание! Головоломки в стиле судоку вам кажутся элементарными? Тогда протестируйте свой интеллект с еще одной головоломкой японского происхождения – какуро. Какуро считается более сложной головоломкой по сравнению с судоку и требует от игрока отличных математических способностей и умения мыслить логически.

Ваша цель – вписать цифры от 1 до 9 во все ячейки поля в соответствии с данными подсказками. Цифры в специальных ячейках указывают сумму, которую вы должны составить из вписываемых цифр. Цифры в одной ячейке не должны повторяться! В горизонтальных ячейках цифры должны быть расположены по возрастанию, в вертикальных – по убыванию. Останавливаться на достигнутом здесь не придется: каждая новая головоломка будет сложнее предыдущей!

Глава 5. Гимнастика для ума.

А теперь предлагаем несколько задач на иссле­дование и построение магических фигур.

Волшебные квадраты 4x4

Найдите как можно больше свойств изображен­ных на рис. 8 магических квадратов 4-го порядка.

Рисунок 8

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8 9 10