Какуро
4 | 10 | 7 | 16 | |||
3 |
| 9 | ||||
7 | 11 | 13 10 |
| |||
11 | 5 | 1 | ||||
7 | 1 | 10 | ||||
6 7 | 2 | |||||
10 3 | 2 | 3 | 3 | |||
3 | 3 | |||||
5 | 4 |
Уровень №1
|
| 15 | 15 | 7 | 4 | 16 |
|
| 20 |
|
|
|
| 9 |
|
| 15 4 |
| 2 |
|
|
| 3 |
10 |
|
|
| 3 12 |
|
| |
6 |
|
| 1 | 9 14 |
|
|
|
7 | 7 10 |
|
|
| 10 | ||
3 |
|
| 13 13 |
| 7 |
| 24 |
14 | 2 |
| 8 |
| 8 |
|
|
17 |
|
|
|
| 12 |
|
|
7 |
|
|
| 10 |
|
|
Уровень №2
Заключение
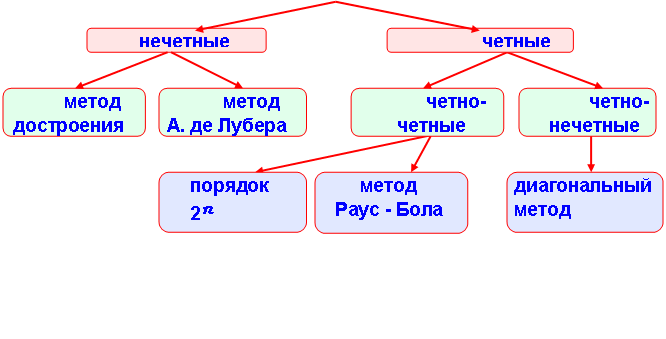В работе рассмотрены вопросы, связанные с историей развития одного из вопросов математики, занимавшего умы очень многих великих людей - магических квадратов. Несмотря на то, что собственно магические квадраты не нашли широкого применения в науке и технике, они подвигли на занятия математикой множество незаурядных людей и способствовали развитию других разделов математики.……………………………………………………. . Работая над проблемой заполнения квадратов, я пришла к выводу, что общий метод построения квадратов неизвестен, хотя широко применяются различные частные алгоритмы. Я систематизировала изученный материал и представила его в виде следующей схемы:
Используя один из этих методов можно заполнить квадрат любого размера. Я составила 8 квадратов разного размера от 3*3 до10*10.
В результате работы я подтвердила гипотезу о том, что существуют способы заполнения магических квадратов, изучив которые можно составить магический квадрат любого порядка.
Ближайшие родственники магических квадратов - латинские квадраты нашли многочисленные применения как в математике, так и в ее приложениях при постановке и обработке результатов экспериментов. В данной работе приведен пример постановки такого эксперимента в агротехнике. Так же я выяснила, что латинские квадраты применяются при шифровании текстов.
По результатам проведённого мною исследования и полученного материала можно сделать следующие выводы:
1. У чисел есть своя собственная жизнь и свои законы;
2. Магическим квадратом n-го порядка называется квадратная таблица размером n х n, заполненная натуральными числами от 1 до n2, суммы которых по всем строкам, столбцам и обеим диагоналям одинаковы.
3. Каждый квадрат, определённого порядка строится по своей методике;
4. У каждого квадрата свои свойства и тайны;
5. Латинским квадратом – называется квадрат n x n клеток, в которых написаны числа 1,2,3,…,n, притом, что в каждой строке и каждом столбце встречаются все эти числа по одному разу;
6.Построение магических квадратов является интересным и увлекательным занятием и одновременно служит хорошей гимнастикой для ума, а так же способствует большему интеллектуальному развитию учащихся;
7.Судоку развивает мышление и логику в каждом из нас. Проведенные исследования доказали улучшение памяти, мышления, а также препятствие развитию и даже излечение заболеваний связанных с головным мозгом! (таких, как болезнь Альцгеймера) Поэтому, ученые рекомендуют ежедневно решать головоломки судоку.
Этот проект можно использовать на внеклассных занятиях для более широкого кругозора учеников, и как разминочные задания к началу урока, при подготовке к олимпиадам и интеллектуальным соревнованиям по математике.
Список использованной литературы:
1. Климченко для любознательных: Кн. для учащихся 5-6 кл.-М.: Просвещение, 1999.
2. Файнштейн магический квадрат // Математика в школе, 2000, №3
3. Энциклопедический словарь юного математика: Сост. Э – 68 – М.: Педагогика, 1989. – 352 с.: ил.
4. Сарвина математика // Математика для школьников 2005, №4
5. www. gamesday. ru/2668-kakuro-sudoku-yaponskie-golovolomki. html
6. http://rk6.bmstu.ru/electronic_book/posapr/zadanpo/kvadrat.htm
7. http://www.krugosvet.ru/articles/15/1001543/print.htm
8. Судоку №5 · 11.03.2009 · Выпускается ИД "Бурда"
9. Судоку №19 · 23.09.2009 · Выпускается ИД "Бурда"
10. Судоку. Спецвыпуск "Какуро" №10 · 20.09.2009
|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 10 |
