или его обобщение — суммирование с весами:

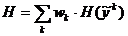(2.3)

где wk ≥ 0 – вес k-го примера.

Веса wk используются для управления вкладом каждого примера в целевое решение и могут применяться в следующих случаях:

1.  Примеры выборки имеют различную информативность.

2.  Неравнозначность примеров, представленных в выборке.

Аналогичные оценки могут быть использованы для оценки работы предиктора на валидационной и тестовой выборках. Решением оптимизационной задачи будет набор настроечных коэффициентов из множества допустимых значений A, обеспечивающих глобальный минимум функции H().

Затем обученный предиктор проверяется на тестовой выборке и делается вывод о качестве предсказания. Качество прогноза предиктором временного ряда во многом зависит от обучающей выборки, функции оценки и используемого семейства адаптивных предикторов, поэтому проблемы их выбора являются одними из наиболее важных.

Совокупность предиктора, ограничений, процедуры настройки и прогнозирования называется предикторной схемой, обозначается символом «П» и описывать следующим образом:

П = (φ, ПН, ПП, ОП) (2.4)

где φ – предиктор, ПН – процедура настройки, ПП –процедура прогнозирования, ОП – ограничения предиктора.

Прогнозирование значений временного ряда

Общая схема прогнозирования временного ряда содержит два этапа: подготовительный и основной. На первом этапе происходит сбор информации о предсказывающих свойствах каждой из предикторных схем, а на втором – прогнозирование участка временного ряда предикторной схемой, которая показала лучшие предсказывающие свойства.

Подготовительный и основной этапы представлены соответственно на Рис. 2.3.

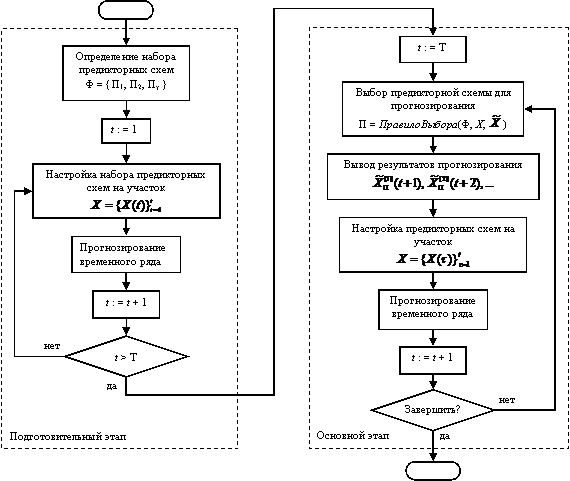
Рис. 2.3 Схема подготовительного и основного этапов

Для определения предикторной схемы с лучшими предсказывающими свойствами используется правило выбора. Это правило на основе реальных и прогнозных значений временного ряда оценивает работу (согласно некоторому критерию H) каждой предикторной схемы из набора Ф, а затем выбирает лучшую из них. Предикторная схема, выбранная с помощью данного правила, называется ведущей. Используем следующее правило: для прогнозирования временного ряда в момент времени t будет применяться предикторная схема с минимальным значением критерия H на данный момент; если таких схем несколько, то выбирается любая из них. Формально это записывается таким образом:

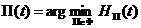(2.5)

Можно привести несколько примеров критериев оценки качества работы предикторных схем: модуль ошибки предсказания, взвешенная сумма квадратов ошибок предсказания и взвешенная сумма ошибок предсказания с разной глубиной прогноза.

Если некоторый предиктор с заданной точностью предсказывает достаточно длинный участок временного ряда, то с высокой степенью уверенности можно говорить о том, что используемый предиктор на данном участке достаточно точно описывает динамику этого ряда. Если после некоторого шага ошибка предсказания начинает существенно возрастать, то можно говорить о нарушении закономерности, зафиксированной в данном предикторе, и появлении разладки. Разладка может свидетельствовать о нарушении закономерности в динамике этого ряда.

Для практических приложений может представлять интерес следующее правило выбора. Если выбрана некоторая предикторная схема, то она остается ведущей до тех пор, пока выдаваемый ею прогноз удовлетворяет заданному пользователем критерию. Если ошибка предсказания временного ряда начинает существенно возрастать, то это означает, что данная предикторная схема непригодна для дальнейшего прогнозирования. В этом случае будем говорить о разладке – ситуации, когда ведущая предикторная схема не удовлетворяет некоторому заданному критерию качества.

Понятие «разладка» подробно рассмотрено в работах [9, 10]. В общем виде его можно описать следующим образом. Задаются две модели некоторого исследуемого временного ряда M0 и M1, при этом считается, что временной ряд до разладки имеет модель M0, а после нее – модель M1. Разладка определяется как момент переключения между моделями M0 и M1.

Классическим примером описания разладки является случай, когда элементы временного ряда xt задаются нормальным распределением, и тогда разладка заключается в изменении значения математического ожидания в некоторый неизвестный момент времени (момент разладки t0).

Рассматриваемые разладки – это участки смены моделей. Сами модели понимаются как предикторные схемы, дающие удовлетворительное описание ряда.

Принципиальный момент: точки разладки зависят от используемых классов предикторов и могут смещаться, исчезать и возникать при изменении этих классов. Разладка – это изменение закономерности, а множество всех используемых закономерностей заранее определено.

Теорема Такенса и погружение

Задача предсказания временного ряда может быть сведена к типовой задаче аппроксимации функции многих переменных по заданной выборке с помощью процедуры погружения этого ряда в многомерное пространство. Смысл ее заключается в формировании набора примеров, состоящих из значений временного ряда в последовательные моменты времени:

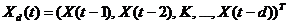(2.6)

Для динамических систем доказана следующая теорема Такенса [11]. Если временной ряд порождается некоторой динамической системой и значения X(t) определяются произвольной функцией состояния такой системы, то существует такая глубина предыстории d, которая обеспечивает однозначное предсказание следующего значения временного ряда. Считается, что при достаточно большой величине d можно гарантировать однозначное прогнозирование будущих значений ряда от его d предыдущих значений: . Выбор величины d может быть произведен эмпирическим методом.

Сложность применения данной теоремы заключается в следующем. Во-первых, при сделанных фундаментальных предположениях о природе временного ряда его зависимость не фиксирована, а может изменяться. В частности, может изменяться глубина предыстории X(t); при попытке восстановить такую зависимость предиктором с фиксированным X(t) в одном случае при большей реальной глубине предыстории будет наблюдаться нехватка параметров, в другом — часть параметров будут мешающими. В обоих случаях качество прогноза будет ухудшаться. Во-вторых, объем выборки может оказаться недостаточным, чтобы достаточно точно восстановить зависимость. Кроме того, может изменяться горизонт прогнозирования, в случае если прогноз производится на несколько шагов вперед. Эти и другие варианты нарушения закономерности во временном ряде сложной структуры могут привести к появлению разладок.

3.4  Решение задачи применением ИНС

Одним из наиболее перспективных подходов к построению прогнозирующих систем является применение математического аппарата основной парадигмы искусственных нейронных сетей.

ИНС используется тогда, когда неизвестен точный вид связей между входами и выходами. Зависимость между значениями входных и выходных переменных находится в процессе обучения сети. Если сеть обучена правильно, она приобретает способность моделировать неизвестную функцию, связывающую значения входных и выходных переменных, и впоследствии такую сеть можно использовать для прогнозирования в ситуации, когда выходные значения неизвестны.

Задачи предсказания или прогнозирования являются, по-существу, задачами построения регрессионной зависимости выходных данных от входных. Нейронные сети могут эффективно строить сильно нелинейные регрессионные зависимости. К тому же нейронные сети могут одновременно решать несколько задач регрессии и/или классификации.

Специфика такова, что, поскольку решаются в основном неформализованные задачи, то конечной целью решения является не построение понятной и теоретически обоснованной зависимости, а получение устройства-предсказателя.

Метод прогнозирования

На НС задача прогнозирования формализуется через задачу рас­познавания образов. Данные о прогнозируемой переменной за некото­рый промежуток времени образуют образ, класс которого определяет­ся значением прогнозируемой переменной в некоторый момент времени за пределами данного промежутка, т. е. значением переменной через интервал прогнозирования.

На этом подходе основан метод окон, предполагающий использование двух окон Wi и Wo с фиксированными размерами n и m соответствен­но (Рис. 2.4).

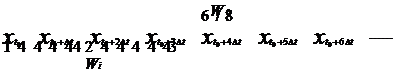
Рис. 2.4 Иллюстрация метода окон

Эти окна, способны перемещаться с некоторым шагом по времен­ной последовательности исторических данных, начиная с первого элемента, и предназначены для доступа к данным временного ряда, причем первое окно Wi, получив такие данные, передает их на вход нейронной сети, а второе – Wo – на выход. Получающаяся на каждом шаге пара:

Wi → Wo (2.7)

используется как элемент обучающей выборки (распознаваемый образ, или наблюдение).

Например, пусть есть данные о ежедневных продажах какого-нибудь фарм. препарата (k = 16):

94… (2.8)

Пусть n = 4, m = 1, s = 1. С по­мощью метода окон для нейронной сети будет сгенерирована следую­щая обучающая выборка:

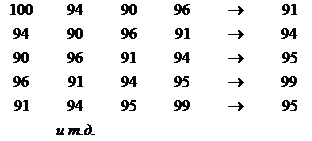(2.9)

Каждый следующий вектор получается в результате сдвига окон Wi и Wo вправо на один элемент (s = 1). Предполагается наличие скрытых зависимостей во временной последовательности как множест­ве наблюдений. Нейронная сеть, обучаясь на этих наблюдениях и со­ответственно настраивая свои коэффициенты, пытается извлечь эти закономерности и сформировать в результате требуемую функцию прогноза P.

Прогнозирование осуществляется по тому же принципу, что и формирование обучающей выборки. При этом выделяются две возмож­ности: одношаговое и многошаговое прогнозирование.

Многошаговое прогнозирование используется для осуществления долгосрочного прогноза и предназначено для определения основного тренда и главных точек изменения тренда для некоторого промежутка времени в будущем. При этом прогнозирующая система использует по­лученные (выходные) данные для моментов времени k+1, k+2 и т. д. в качестве входных данных для прогнозирования на моменты времени k+2, k+3 и т. д.

Предположим, система обучилась на временной последователь­ности (2.8). Затем она спрогнозировала k+1 элемент последователь­ности, например, равный 95, когда на ее вход был подан последний из известных ей образов (99, 98, 96, 98). После этого она осу­ществляет дальнейшее прогнозирование и на вход подается следующий образ (98, 96, 98, 95). Последний элемент этого образа является прогнозом системы. И так далее.

Одношаговое прогнозирование используется для краткосрочных прогнозов, обычно – абсолютных значений последовательности. Осу­ществляется прогноз только на один шаг вперед, но используется реальное, а не прогнозируемое значение для осуществления прогноза на следующем шаге.

Для временной последовательности (2.8). На шаге k + 1 система прогнозирует требование 95, хотя реальное значение должно быть 96. На шаге k + 2 в качестве входного образа будет использоваться образ (98, 96, 98, 96).

Как было сказано выше, результатом прогноза на НС является класс к которому принадлежит переменная, а не ее конкретное зна­чение. Формирование классов должно проводиться в зависимости от того каковы цели прогнозирования. Общий подход состоит в том, что область определения прогнозируемой переменной разбивается на классы в соответствии с необходимой точностью прогнозирования. Классы могут представлять качественный или численный взгляд на изменение переменной.

Прогнозирование на НС обладает рядом недостатков. Необходимо иметь как достаточно много наблюдений для создания приемлемой модели. Это достаточно большое число данных и существует много случаев, когда такое количество исторических данных недоступно. Однако, необходимо отметить, что можно постро­ить удовлетворительную модель на НС даже в условиях нехватки дан­ных. Модель может уточняться по мере того, как свежие данные ста­новится доступными.

Другим недостатком нейронных моделей – значительные затраты по времени и другим ресурсам для построения удовлетворительной модели. Эта проблема не очень важна, если исследуется небольшое число временных последовательностей.

Однако, несмотря на перечисленные недостатки, модель облада­ет рядом достоинств. Существует удобный способ модифицировать модель, по мере того как появляются новые наблюдения. Модель хорошо работает с временными последовательностями, в которых мал интер­вал наблюдений, т. е. может быть получена относительно длительная временная последовательность. По этой причине модель может быть использована в областях, где интересуют ежеднев­ные или еженедельные наблюдения. Эти модели также используются в ситуациях, когда необходимо анализировать относительно небольшое число времен­ных последовательностей.

Информационная ёмкость ИНС

Для сетей с числом слоев больше двух, он остается открытым. Как показано в [12], для НС с двумя слоями, то есть выходным и одним скрытым слоем, детерминистская емкость сети Cd оценивается так:

Nw/Ny<Cd<Nw/Ny×log(Nw/Ny) (2.10)

где Nw – число подстраиваемых весов, Ny – число нейронов в выходном слое.

Следует отметить, что данное выражение получено с учетом некоторых ограничений. Во-первых, число входов Nx и нейронов в скрытом слое Nh должно удовлетворять неравенству Nx+Nh>Ny. Во-вторых, Nw/Ny>1000. Однако вышеприведенная оценка выполнялась для сетей с активационными функциями нейронов в виде порога, а емкость сетей с гладкими активационными функциями обычно больше [12]. Кроме того, фигурирующее в названии емкости прилагательное "детерминистский" означает, что полученная оценка емкости подходит абсолютно для всех возможных входных образов, которые могут быть представлены Nx входами. В действительности распределение входных образов, как правило, обладает некоторой регулярностью, что позволяет НС проводить обобщение и, таким образом, увеличивать реальную емкость. Так как распределение образов, в общем случае, заранее не известно, мы можем говорить о такой емкости только предположительно, но обычно она раза в два превышает емкость детерминистскую.

В продолжение разговора о емкости НС логично затронуть вопрос о требуемой мощности выходного слоя сети, выполняющего окончательную классификацию образов. Дело в том, что для разделения множества входных образов, например, по двум классам достаточно всего одного выхода. При этом каждый логический уровень – "1" и "0" – будет обозначать отдельный класс. На двух выходах можно закодировать уже 4 класса и так далее. Однако результаты работы сети, организованной таким образом, можно сказать – "под завязку", – не очень надежны. Для повышения достоверности классификации желательно ввести избыточность путем выделения каждому классу одного нейрона в выходном слое или, что еще лучше, нескольких, каждый из которых обучается определять принадлежность образа к классу со своей степенью достоверности, например: высокой, средней и низкой. Такие НС позволяют проводить классификацию входных образов, объединенных в нечеткие (размытые или пересекающиеся) множества. Это свойство приближает подобные НС к условиям реальной жизни.

Архитектура нейронной сети

Среди различных структур нейронных сетей (НС) одной из наиболее известных является многослойная структура, в которой каждый нейрон произвольного слоя связан со всеми аксонами нейронов предыдущего слоя или, в случае первого слоя, со всеми входами НС. Такие НС называются полносвязными. Когда в сети только один слой, алгоритм ее обучения с учителем довольно очевиден, так как правильные выходные состояния нейронов единственного слоя заведомо известны, и подстройка синаптических связей идет в направлении, минимизирующем ошибку на выходе сети. По этому принципу строится, например, алгоритм обучения однослойного персептрона. В многослойных же сетях оптимальные выходные значения нейронов всех слоев, кроме последнего, как правило, не известны, и двухслойный или более персептрон уже невозможно обучить, руководствуясь только величинами ошибок на выходах НС. Один из вариантов решения этой проблемы – разработка наборов выходных сигналов, соответствующих входным, для каждого слоя НС, что, конечно, является очень трудоемкой операцией и не всегда осуществимо. Второй вариант – динамическая подстройка весовых коэффициентов синапсов, в ходе которой выбираются, как правило, наиболее слабые связи и изменяются на малую величину в ту или иную сторону, а сохраняются только те изменения, которые повлекли уменьшение ошибки на выходе всей сети. Третий вариант – распространение сигналов ошибки от выходов НС к ее входам, в направлении, обратном прямому распространению сигналов в обычном режиме работы.

Алгоритм обучения ИНС

После того, как определено число слоев и число элементов в каждом из них, необходими нйти значения весов и порогов сети, которые бы минимизировали ошибку прогноза, выдаваемого сетью. Для этого применяются процедуры обучения ИНС.

Одной из классических и самой распространенной процедурой обучения ИНС является алгоритм обратного распространения ошибки (back propagation), подробно описанный в [13, 14, 15, 16, 17, 18, 19]. Его суть заключается в следующем.

Согласно методу наименьших квадратов, минимизируемой целевой функцией ошибки НС является величина:

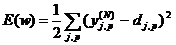(2.11)

где – реальное выходное состояние нейрона j выходного слоя N нейронной сети при подаче на ее входы p-го образа; djp – идеальное (желаемое) выходное состояние этого нейрона.

Суммирование ведется по всем нейронам выходного слоя и по всем обрабатываемым сетью образам. Минимизация ведется методом градиентного спуска, что означает подстройку весовых коэффициентов следующим образом:

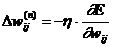(2.12)

Здесь wij – весовой коэффициент синоптической связи, соединяющей i-ый нейрон слоя n-1 с j-ым нейроном слоя n, h – коэффициент скорости обучения, 0<h<1.

Как показано в [20],

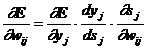(2.13)

Здесь под yj, как и раньше, подразумевается выход нейрона j, а под sj – взвешенная сумма его входных сигналов, то есть аргумент активационной функции. Так как множитель dyj/dsj является производной этой функции по ее аргументу, из этого следует, что производная активационной функция должна быть определена на всей оси абсцисс. В связи с этим функция единичного скачка и прочие активационные функции с неоднородностями не подходят для рассматриваемых НС. В них применяются такие гладкие функции, как гиперболический тангенс или классическая сигмоида с экспонентой. В случае гиперболического тангенса

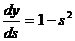(2.14)

Третий множитель ¶sj/¶wij, очевидно, равен выходу нейрона предыдущего слоя yi(n-1).

Первый множитель в (2.13) легко раскладывается следующим образом [20]:

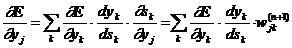(2.15)

Здесь суммирование по k выполняется среди нейронов слоя n+1.

Введя новую переменную

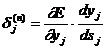(2.16)

получим рекурсивную формулу для расчетов величин dj(n) слоя n из величин dk(n+1) более старшего слоя n+1.

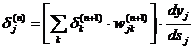(2.17)

Для выходного же слоя

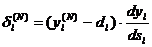(2.18)

Запишем (2.12) в раскрытом виде:

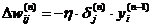(2.19)

Иногда для придания процессу коррекции весов некоторой инерционности, сглаживающей резкие скачки при перемещении по поверхности целевой функции, (2.19) дополняется значением изменения веса на предыдущей итерации

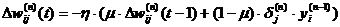(2.20)

где m – коэффициент инерционности, t – номер текущей итерации.

Таким образом, полный алгоритм обучения НС с помощью процедуры обратного распространения строится так:

1.  Подать на входы сети один из возможных образов и в режиме обычного функционирования НС, когда сигналы распространяются от входов к выходам, рассчитать значения последних. Учитывая, что

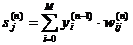(2.21)

где M – число нейронов в слое n-1 с учетом нейрона с постоянным выходным состояние m +1, задающего смещение; yi(n-1)=xij(n) – i-ый вход нейрона j слоя n.

yj(n) = f(sj(n)), где f(…) – сигмоид (2.22)

yq(0)=Iq, (2.23)

где Iq – q-ая компонента вектора входного образа.

2.  Рассчитать d(N) для выходного слоя по формуле (2.18).

3.  Рассчитать по формуле (2.19) или (2.20) изменения весов Dw(N) слоя N.

4.  Рассчитать по формулам (2.17) и (2.19) (или (2.17) и (2.20)) соответственно d(n) и Dw(n) для всех остальных слоев, n = N-1,...1.

5.  Скорректировать все веса в НС

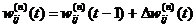(2.24)

6.  Если ошибка сети существенна, перейти на шаг 1. В противном случае – конец.

Сети на шаге 1 попеременно в случайном порядке предъявляются все тренировочные образы, чтобы сеть, образно говоря, не забывала одни по мере запоминания других. Алгоритм иллюстрируется на Рис. 2.5.

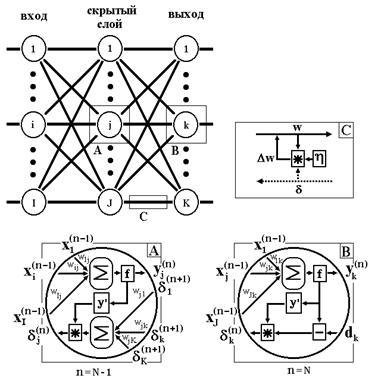
Рис. 2.5 Диаграмма сигналов в сети при обучении по алгоритму back propagation

Из выражения (2.19) следует, что когда выходное значение yi(n-1) стремится к нулю, эффективность обучения заметно снижается. При двоичных входных векторах в среднем половина весовых коэффициентов не будет коррек­тироваться [21], поэтому область возможных значений выходов нейронов [0, 1] желательно сдвинуть в пределы [-0.5,+0.5], что достигается простыми модификациями логистических функций. Например, сигмоида с экспонентой преобразуется к виду:

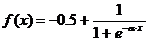(2.25)

В процессе обучения может возникнуть ситуация, когда большие положительные или отрицательные значения весовых коэффициентов сместят рабочую точку на сигмоиде многих нейронов в область насыщения. Малые величины производной от логистической функции приведут в соответствие с (2.17) и (2.18) к остановке обучения, что парализует НС.

Во-вторых, применение метода градиентного спуска не гарантирует, что будет найден глобальный, а не локальный минимум целевой функции. Эта проблема связана еще с одной, а именно – с выбором величины скорости обучения. Доказательство сходимости обучения в процессе обратного распространения основано на производных, то есть приращения весов и, следовательно, скорость обучения должны быть бесконечно малыми, однако в этом случае обучение будет происходить неприемлемо медленно. С другой стороны, слишком большие коррекции весов могут привести к постоянной неустойчивости процесса обучения. Поэтому в качестве h обычно выбирается число меньше 1. Кроме того, для исключения случайных попаданий в локальные минимумы иногда, после того как значения весовых коэффициентов стабилизируются, h кратковременно сильно увеличивают, чтобы начать градиентный спуск из новой точки. Если повторение этой процедуры несколько раз приведет алгоритм в одно и то же состояние НС, можно более или менее уверенно сказать, что найден глобальный минимум.

Выбор и представление набора данных для ИНС

Если задача решается с помощью нейронной сети, то необходимо собрать данные для её обучения. Обучающий набор представляет собой ряд наблюдений, для которых указаны значения входных и выходных переменных. Выбор переменных осуществляется исходя из анализа предметной области. Необходимо выбирать такие переменные, которые предположительно влияют на результат.

Любая ИНС принимает на входе числовые значения и выдает на выходе также числовые значения. Поэтому перед подачей на вход сети данных их необходимо нормировать. Простую нормировку выполняют заменой каждой компоненты входного вектора данных xi величиной:

(2.26)

где max xi и min xi – соответственно максимальное и минимальное значение для данной компоненты, вычисленные по всей обучающей выборке. По этой же формуле пересчитываются и компоненты векторов ответов.

Если предполагается, что в дальнейшем поступят сильно отличающиеся данные, то min и max-величины задаются пользователем по его оценкам. Эти величины должны вводиться в момент создания сети и в дальнейшем не зависеть от обучающей выборки.

Функции активации элементов сети обычно выбираются таким образом, чтобы ее входной аргумент мог принимать произвольные значения, а выходные значения лежали в строго ограниченном диапазоне («сплющивание»). Выходные сигналы сети должны нормироваться в диапазон истинных значений по обращенным формулам.

Коль скоро выходные значения всегда принадлежат некоторой ограниченной области, а вся информация должна быть представлена в числовом виде, очевидно, что при решении реальных задач методами ИНС требуются этапы предварительной обработки – пре-процессирования и заключительной обработки – пост-процессирования данных [22].

Нейронные сети могут эффективно работать с числовыми данными, лежащими в только определенном ограниченном диапазоне. Это создает проблемы в тех случаях, когда данные имеют нестандартный масштаб, включают пропущенные значения или являются номинальными или нечисловыми. Для устранения этой проблемы применяются следующие методы обработки:

·  числовые данные масштабируются в подходящий для сети диапазон;

·  пропущенные значения заменяются средним значением этой переменной по всем имеющимся обучающим выборкам или другим статистическим значением [22];

·  номинальные или нечисловые переменные преобразуются в числовую форму

За преобразование информации от выходных элементов в выходную переменную и представление результатов отвечает этап пост-процессирования.

4.  Разработка СППР

4.1  Общие требования к разрабатываемой системе

В данном случае принятия решений в торговой деятельности предприятия объектом исследования является товарооборот, его признаками – показатели его финансово-хозяйственной деятельности (максимальная прибыль и минимальные убытки), а исследуемым свойством – ликвидность товарных остатков на складе. Прогнозирование в задаче рассматривается в целях планирования управления запасами (Рис. 3.1).

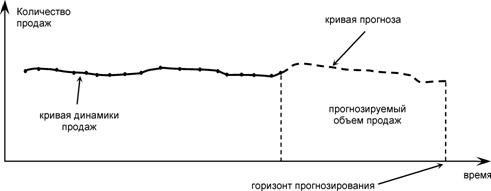
Рис. 3.1 Кривая прогноза и динамики продаж

Таким образом, интерес решения задачи лежит в определении будущих продаж товара. Полагая именно такую направлен­ность и учитывая особенности ведения бухгалтерского учета на предприятии, сформулируем основные принципы решения проблемы проектирования СППР:

·  проектируемая система должна осуществлять выявление и интерполяцию скрытых закономерностей потребительского спроса из исторических данных динамики продаж, а также обладать функцией прогноза количества продаж в единичном базисе на период до половины срока годности препарата;

·  на основании прогноза продаж, закупочной цены и с учетом остатка товарного запаса на момент принятия решения система должна предлагать ЛПР наиболее подходящий вариант закупок по количеству и ассортименту, исходя из максимума прибыли предприятия;

·  прогнозирующая система должна идентифицировать постоянные изменения и подстраивать модель прогнозирования под изменения в процессе;

·  прогнозирующая система также не должна реагировать на необычные, экстраординарные наблюдения;

·  система должна обладать простым и интуитивно-понятным интерфейсом, быть легкой в эксплуатации и ориентированной на непрограммирующего пользователя;

·  система должна иметь не большой объем и низкую стоимость, а также должна быть совместима с уже используемой учетно-аналитической системой.

4.2  Разработка логической структуры СППР

Современные бухгалтерские системы – это системы поддержки принятия решений, предназначенные для квалифицированных специалистов и позволяющие не только автоматизировать все учетные задачи, но и получать своевременную и оперативную финансовую информацию для повышения эффективности управления предприятием. Учетная информация, накапливаемая в этих системах, представляет большую ценность для руководителей и аналитиков в их повседневной деятельности. Источником информации для проведения статистического анализа являются финансовые отчеты (бухгалтерский баланс предприятия, отчет о финансовых результатах, отчет о движении денежных средств, приложение к балансу).

Одним из наиболее перспективных направлений применения технологий интеллектуального анализа учетных данных являются бизнес-приложения в составе интегрированных бухгалтерских систем. И для обеспечения минимальных трудозатрат на разработку пользовательского интерфейса, минимизации объема программного кода и упрощения проблемы интеграции разработку намеченной системы прогнозирования решено было выполнить в качестве встраиваемого модуля в уже использующуюся учетно-аналитическую систему «1С: Предприятие 7.7».

Подобный подход ориентирован в основном на непрограммирующего пользователя и на решение конкретных задач. От пользователя этой системы при этом не требуется специальных знаний в области БД, факторного анализа или методов оптимизации.

Технология статистической обработки данных базируется на использовании многомерных статистических процедур, из которых наибольшее практическое применение получили методы кластерного анализа и прогнозирования временных рядов.

Выделить группы с однородными данными, расчленить информацию на однокачественные интервалы или, иными словами, сгруппировать данные по типу (типология исходной информации) – это начальный этап предварительного анализа данных, причем для различных объектов статистических измерений используют соответствующие средства типологической группировки.

Для временных рядов этим целям призвана служить периодизация – разбиение динамических рядов на интервалы однокачественного развития.

Основная проблема в задаче анализа и прогнозирования временных рядов заключается в построении модели, адекватно отражающей их динамику. Рыночный механизм, характеризующийся огромным количеством постоянно меняющихся связей, зависит от множества внешних факторов, способных существенно повлиять на всю структуру его зависимостей, причем воздействие может быть самым разнообразным.

Для решения проблемы прогнозирования удобнее выбрать практический подход и использовать технические средства анализа временных рядов и в качестве адаптивного предиктора использовать многослойную нейронную сеть.

Исходя из общих требований к системе п. 3.1, спецификации программы «1С: Предприятие 7.7» [23] и учитывая содержание п. 2 предполагается следующая идеология решения данной проблемы:

I.  Основную обработку данных (прогноз) производить в подключаемом внешнем модуле, для чего разработать по технологии ActiveX компонент, содержащий программный код обработки.

II.  В качестве адаптивного предиктора для прогнозирования использовать трехслойную ИНС.

III.  Обучение сети проводить по алгоритму обратного распространения ошибки;

IV.  Пре - и пост прецессионную обработку данных, а также представление результатов прогнозирования проводить имеющимися средствами системы программ «1С: Предприятие 7.7», для чего дополнительно реализовать форму внешнего отчета, содержащего методы подготовки данных, создания COM объекта и передачи в него данных для обработки.

4.3  Этапы обработки данных

Исходя из анализа предметной области определяем спецификацию необходимых для достижения поставленной цели переменных и сведений (Таблица 1.1).

Таблица 3.1 Спецификация исходных данных.

Спецификация данных, необходимых для процедуры обучения ИНС, представлена в Таблица 3.2.

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8