·  выявление лояльности клиентов.  Data Mining можно использовать для определения характеристик клиентов, которые, один раз воспользовавшись услугами данной компании, с большой долей вероятности останутся ей верными. В итоге средства, выделяемые на маркетинг, можно тратить там, где отдача больше всего.

Страхование

Страховые компании в течение ряда лет накапливают большие объемы данных. Здесь обширное поле деятельности для методов Data Mining:

·  выявление мошенничества. Страховые компании могут снизить уровень мошенничества, отыскивая определенные стереотипы в заявлениях о выплате страхового возмещения, характеризующих взаимоотношения между юристами, врачами и заявителями;

·  анализ риска. Путем выявления сочетаний факторов, связанных с оплаченными заявлениями, страховщики могут уменьшить свои потери по обязательствам. Известен случай, когда в США крупная страховая компания обнаружила, что суммы, выплаченные по заявлениям людей, состоящих в браке, вдвое превышает суммы по заявлениям одиноких людей. Компания отреагировала на это новое знание пересмотром своей общей политики предоставления скидок семейным клиентам.

Медицина

Известно много экспертных систем для постановки медицинских диагнозов. Они построены главным образом на основе правил, описывающих сочетания различных симптомов различных заболеваний. С помощью таких правил узнают не только, чем болен пациент, но и как нужно его лечить. Правила помогают выбирать средства медикаментозного воздействия, определять показания – противопоказания, ориентироваться в лечебных процедурах, создавать условия наиболее эффективного лечения, предсказывать исходы назначенного курса лечения и т. п. Технологии Data Mining позволяют обнаруживать в медицинских данных шаблоны, составляющие основу указанных правил.

Молекулярная генетика и генная инженерия

Пожалуй, наиболее остро и вместе с тем четко задача обнаружения закономерностей в экспериментальных данных стоит в молекулярной генетике и генной инженерии. Здесь она формулируется как определение так называемых маркеров, под которыми понимают генетические коды, контролирующие те или иные фенотипические признаки живого организма. Такие коды могут содержать сотни, тысячи и более связанных элементов.

На развитие генетических исследований выделяются большие средства. В последнее время в данной области возник особый интерес к применению методов Data Mining. Известно несколько крупных фирм, специализирующихся на применении этих методов для расшифровки генома человека и растений.

Прикладная химия

Методы Data Mining находят широкое применение в прикладной химии (органической и неорганической). Здесь нередко возникает вопрос о выяснении особенностей химического строения тех или иных соединений, определяющих их свойства. Особенно актуальна такая задача при анализе сложных химических соединений, описание которых включает сотни и тысячи структурных элементов и их связей.

Предметно-ориентированные аналитические системы

Предметно-ориентированные аналитические системы очень разнообразны. Наиболее широкий подкласс таких систем, получивший распространение в области исследования финансовых рынков, носит название "технический анализ". Он представляет собой совокупность нескольких десятков методов прогноза динамики цен и выбора оптимальной структуры инвестиционного портфеля, основанных на различных эмпирических моделях динамики рынка. Эти методы часто используют несложный статистический аппарат, но максимально учитывают сложившуюся своей области специфику (профессиональный язык, системы различных индексов и пр.). На рынке имеется множество программ этого класса. Как правило, они довольно дешевы (обычно $300–1000).

2.3.4  Прогнозирующие системы

Прогноз и цели его использования

Ключевым моментом принятия решения в управлении экономическим объектом является прогнозирование. Прогноз – это предсказание будущих событий. Целью прогнозирования является уменьшение риска при принятии решения.

Конечная эффективность любого решения зависит от последовательности событий, возникающих уже после принятия реше­ния. Возможность предсказать неуправляемые аспекты этих событий перед принятием решения позволяет сделать наилучший выбор. Поэтому системы планирования и управления, обычно, реализуют функцию прогноза.

Польза прогноза в улучшении принимаемых решений зависит от горизонта прогнозирования и формы прогноза также как и от его точности. При этом прибыль должна измеряться для всей системы управления как единого целого, и прогнозирование – только один элемент этой системы.

Прогнозирующая система должна выполнять две основные функции: генерацию прогноза и управление прогнозом.

Генерация прогноза включает получение данных для уточнения модели прогнози­рования, проведение прогнозирования, учет мнения экспертов и пре­доставление результатов прогноза ЛПР. Управление прогно­зом включает в себя наблюдение процесса прогнозирования для опре­деления неконтролируемых условий и поиск возможности для улучше­ния производительности прогнозирования. Важным компонентом фун­кции управления является тестирование путевого сигнала. Функция управления прогнозом также должна пе­риодически определять производительность прогнозирования и пре­доставлять результаты соответствующему менеджеру. Соотношения между генерацией прогноза и управлением прогнозом показано на Рис. 1.11.

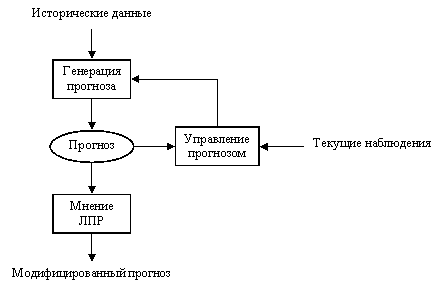
Рис. 1.11 Соотношения между генерацией прогноза и управле­нием прогнозом.

Как правило, прогноз имеет некоторую неточность. Ошибка зависит от используемой прогнози­рующей системы. С увеличением затрачиваемых на прогноз ресурсов растет и его точность, а убытки, связанные с неоп­ределенностью при принятии решений, снижаются. Стоимость прогноза увеличивает­ся по мере того, как уменьшаются убытки от неопределенности (Рис. 1.12). При некотором уровне ошибки прогнозирования общая стоимость затрат на прогнозирова­ние и убытков минимальны.

Концептуальный поход, проиллюстрированный на Рис. 1.12, основан на асимптотическом снижении убытков при использовании результатов прогнозирования. За некоторой точкой, допол­нительные затраты на прогнозирование могут вовсе не приводить к снижению потерь. Это связано с тем, что невозможно снизить сред­нюю ошибку прогнозирования ниже определенного уровня, вне зависи­мости от того насколько сложен примененный метод прогнозирования.

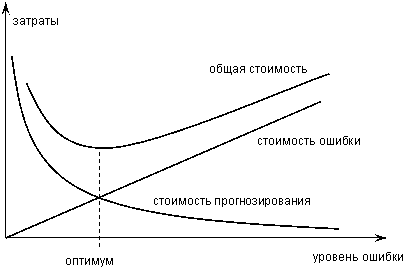
Рис. 1.12 График иллюстрирующий соотношение и эффективность затрат на прогнозирование.

Конечно, стоимость является важным элементом при оценке и сравнении методов прогнозирования. Ее можно разделить на однора­зовые затраты на разработку и установку системы и затраты на ее эксплуатацию. Что касается затрат на эксплуатацию, то разные прогнозирующие процедуры могут очень сильно отличаться по стои­мости получения данных, эффективности вычислений и уровню дей­ствий, необходимых для поддержания системы.

Поскольку прогнозирование никогда не сможет полностью устранить риск при принятии решений, необходимо явно определять не­точность прогноза. Обычно, принимаемое решение определяется ре­зультатами прогноза с учетом возможной ошибки прогнозирования. Можно также сравнивать методы прогнозирования с точки зрения реакции на постоянные изменения во временной последова­тельности, описывающей процесс, и стабильности при случайных и кратковременных изменениях.

Это предполагает, что прогнозирующая система дол­жна обеспечивать определение ошибки прогнозирования, также как и само прогнозирование. Такой подход значительно снижает риск объективно связанный с процессом принятия решений.

Необходимо отметить, что прогнозирование это не конечная цель. Прогнозирующая система это часть большой системы менеджмен­та и как подсистема, она взаимодействует с другими компонентами системы, играя немалую роль в получаемом результате.

Примеры ситуаций [7], в которых целесообразно применение прогнозирующих систем:

Управление материально-производственными запасами

В управ­лении запасами запасных частей на ремонтном предприятии совершенно необходимо оценить степень используемости каждой детали. На основе этой информации определяется необходимое коли­чество запасных частей. Кроме того, необходимо оценить ошибку прогнозирования. Эта ошибка может быть оценена, например, на ос­нове данных о времени, которое понадобилось для доставки деталей, которых не было на складе.

Планирование производства

Для того, чтобы планировать производство семейства продуктов, возможно, необходимо спрогнози­ровать продажу для каждого наименования продукта, с учетом време­ни доставки, на несколько месяцев вперед. Эти прогнозы для конеч­ных продуктов могут быть потом преобразованы в требования к полу­фабрикатам, компонентам, материалам, рабочим и т. д. Таким образом, на основании прогноза может быть построен график работы це­лой группы предприятий.

Финансовое планирование

Финансового менеджера интересует, как будет изменяться денежный оборот компании с течением времени. Менеджер, может пожелать узнать, в какой период времени в буду­щем оборот компании начнет падать, с тем, чтобы принять соответ­ствующее решение уже сейчас.

Разработка расписания персонала

Менеджер почтовой компании должен знать прогноз количества обрабатываемых писем, с тем, что­бы обработка производилась в соответствии с расписанием персона­ла и производительностью оборудования.

Планирование нового продукта

Решение о разработке нового продукта обычно требует долговременного прогноза того, каким спросом он будет пользоваться. Этот прогноз не менее важен, чем определение инвестиций необходимых для его производства.

Управление технологическим процессом

Прогнозирование также может быть важной частью систем управления технологическими про­цессами. Наблюдая ключевые переменные процесса и используя их для предсказания будущего поведения процесса, можно определить опти­мальное время и длительность управляющего воздействия. Например, некоторое воздействие в течение часа может повышать эффектив­ность химического процесса, а потом оно может снижать эффектив­ность процесса. Прогнозирование производительности процесса мо­жет быть полезно при планировании времени окончания процесса и общего расписания производства.

3.  определение проблемы и методы прогнозирования

3.1  Определение проблемы прогнозирования

Результаты прогнозирования используются для поддержки принятия решений. Следовательно, природа принимаемых решений определяет большинство желаемых характеристик прогнози­рующей системы. Изучение предметной области должно помочь найти отве­ты на вопросы о том, что нужно прогнозировать, какую форму дол­жен принять прогноз, какие временные элементы включаются и како­ва желательная точность прогноза.

Первый аспект проблемы прогнозирования связан с тем, что при определении предмета прогнозирования, указы­ваются переменные, которые анализируются и предсказываются. Здесь очень важен требуемый уровень детализации, на который влияет множество факто­ров: базис прогнозирования, доступность и точность данных, стоимость анализа и предпоч­тения ЛПР. Если требуется разнородная результи­рующая информация нельзя однозначно выб­рать анализируемые переменные. В ситуациях, когда наилучший набор переменных неясен, необходимо пробовать разные альтернативы и выбрать один из вариантов, дающий наилучшие результаты. Обычно так осуществляет­ся выбор при разработке прогнозирующих систем, основанных на ана­лизе исторических данных.

Точность прогноза, требуемая для конкретной проблемы, оказы­вает огромное влияние на прогнозирующую систему. Важнейшей характеристикой системы управления яв­ляется ее способность добиваться оптимальности при работе с неоп­ределенностью.

Посредством данных, необходимых для прогнозирующей системы, в систему может подаваться и ошибка, поэтому необходимо редакти­ровать входные данные системы для того, чтобы устранить очевид­ные или вероятные ошибки. Конечно, небольшие ошибки идентифициро­вать будет невозможно, но они обычно не оказывают значительного влияния на прогноз. Более значительные ошибки легче найти и ис­править. Прогнозирующая система также не должна реагировать на необычные, экстраординарные наблюдения.

Второй важный аспект проблемы прогнозирования – это определение следующих трех параметров: периода прогнозирова­ния, горизонта прогнозирования и интервала прогнозирования. Пе­риод прогнозирования – это основная единица времени, на которую делается прогноз. Горизонт прогнозиро­вания – это число периодов в будущем, которые покрывает прогноз. Наконец, интервал прогнозирования – частота, с которой делается новый прогноз. Часто интервал прогнозирования совпадает с периодом прогнозирования. В этом случае прогноз пе­ресматривается каждый период, используя требование за последний период и другую текущую информацию в качестве базиса для перес­матриваемого прогноза. Если горизонт всегда имеет одну и ту же длину (Т-периодов) и прогноз пересматривается каждый период, то го­ворят, что прогноз осуществляется на основе движущего горизонта. В этом слу­чае, репрогнозируется требование для Т-1 периода и делаем ориги­нальный прогноз для периода Т.

Выбор периода и горизонта прогнозирования обычно диктуется условиями принятия решений в области, для которой производится прогноз. Для того чтобы прогнозирование имело смысл, горизонт прогнозирования должен быть не меньше, чем время, необходимое для реализации решения принятого на основе прогноза. Таким образом, прогнозирование очень сильно зависит от природы принимаемого ре­шения. В некоторых случаях, время, требуемое на реализацию реше­ния, не определено. Существует ме­тоды работы в условиях подобной неопределенности, но они повы­шают вариацию ошибки прогнозирования. Поскольку с увеличением го­ризонта прогнозирования точность прогноза, обычно, снижается, часто мы можем улучшить процесс принятия решения, уменьшив время, необходимое на реализацию решения и, следовательно, уменьшив го­ризонт и ошибку прогнозирования.

Интервал прогнозирования часто определяется операционным ре­жимом системы обработки данных, которая обеспечивает информацию о прогнозируемой переменной. В том случае, если уровень продаж сообщается ежемесячно, возможно для еженедельного прогноза про­даж этих данных недостаточно и интервал прогнозирования месяц – является более обоснованным. При определении интервала прогнозирования необходимо выби­рать между риском не идентифицировать изменения в прогнозируемом процессе и стоимостью прогноза. Если используется значительный период прогнозирования, то можно работать достаточно длительное время в соответствии с планами, основанными на, возможно, уже бессмысленном прогнозе. С другой стороны, если используется бо­лее короткий интервал, то приходиться оплачивать не только стои­мость прогнозирования, но и затраты на изменение планов, с тем, чтобы они соответствовали новому прогнозу. Наилучший интервал прогнозирования зависит от стабильности процесса, последствий ис­пользования неправильного прогноза, стоимости прогнозирования и репланирования.

Третьим аспектом прогнозирования является требуемая форма прогноза. Обычно при прогнозировании проводится оценка ожидаемо­го значения переменной, плюс оценка вариации ошибки прогнозирова­ния или промежутка, на котором сохраняется вероятность содержа­ния реальных будущих значений переменной. Этот промежуток назы­вается предсказуемым интервалом.

В некоторых случаях не так важно предсказание конкрет­ных значений прогнозируемой переменной, как предсказание значи­тельных изменений в ее поведении. Такая задача возникает, напри­мер, при управлении технологическими процессами, когда необ­ходимо предсказывать момент перехода процесса в неуправляе­мое состояние.

Существует ряд других факторов, которые также необходимо принимать во внимание при рассмотрении проблемы прогнозирования.

Один из них связан с процессом, генерирующим пе­ременную. Если известно, что процесс стабилен, или существуют постоянные условия, или изменения во времени происходит медленно – прогнозирующая система для такого процесса может достаточно сильно отличаться от системы, которая должна производить прогно­зирование неустойчивого процесса с частыми фундаментальными изме­нениями. В первом случае, необходимо активное использование исто­рических данных для предсказания будущего, в то время как во вто­ром лучше сосредоточиться на субъективной оценке и прогнозирова­нии для определения изменений в процессе.

Еще один фактор – это доступность данных. Исторические данные необходимы для построения прогнозирующих процедур; будущие наблю­дения служат для проверки прогноза. Количество, точность и досто­верность этой информации важны при прогнозировании. Кроме этого необходимо исследовать представительность этих данных.

И, наконец, два важных фактора проблемы прогнозирования – возможности и интерес людей, которые делают и используют прогноз. В идеале, историческая информация анализируется автоматически, и прогноз представляется ЛПР для возможной модификации. Вве­дение эксперта в процесс прогнозирования является очень важным, но требует сотрудничества опытных менеджеров. Далее прогноз пере­дается ЛПР, которые используют его при принятии решений и могут получить реальную пользу от его использования.

Необходимо также отметить вычислительные ограничения прогнозирую­щих систем. Если изредка прогнозируется несколько переменных, то в системе возможно применение более глубоких процедур анализа, чем если необходимо часто прогнозировать большое число перемен­ных. В последней ситуации, необходимо большое внимание уделить разработке эффективного управления данными.

3.2  Анализ методов прогнозирования

Методы прогнозирования можно разделить на два класса квали­тативные и квантитативные, в зависимости от того, какие математи­ческие методы используются.

Квалитативные процедуры производят субъективную оценку, ос­нованную на мнении экспертов. Обычно, это формальная процедура для получения обобщенного предсказывания, на основе ранжирования и обобщения мнения экспертов. Эти процедуры основываются на опросах, тестах, оценке эффектив­ности продаж и исторических данных, но процесс, с помощью которо­го получается прогноз остается субъективным.

С другой стороны, квантитативные процедуры прогнозирования явно объявляют – каким образом получен прогноз. Четко видна логи­ка и понятны математические операции. Эти методы производят ис­следование исторических данных для того, чтобы определить глубин­ный процесс, генерирующий переменную и, предположив, что процесс стабилен, использовать знания о нем для того, чтобы экстраполиро­вать процесс в будущее. К квантитативным процедурам прогнозирова­ния относятся методы, основанные на статистическом анализе, анали­зе временных последовательностей, байесовском прогнозировании, наборе фрактальных методов, нейронных сетях.

Используется два основных типа моделей: модели вре­менных последовательностей и причинные модели.

Временные последовательности – это упорядоченные во времени последовательности наблюдений (реализаций) переменной. Переменная наблюдается через дискретные промежутки времени.

Анализ временных последовательностей включает описание процесса или феномена, который генерирует последовательность, и использует для прогнозирования пе­ременной только исторические данные об ее изменении. Для предсказания временных последовательностей, необходимо предста­вить поведение процесса в виде математической модели, которая мо­жет быть распространена в будущем. Для этого необходимо, чтобы модель хорошо представляла наблюдения в любом локальном сегменте времени, близком к настоящему. Обычно нет необходимости иметь мо­дель, которая представляла бы очень старые наблюдения, так как они не характеризуют настоящий момент. Также нет необходимости представлять наблюдения в далеком будущем, т. е. че­рез промежуток времени больший, чем горизонт прогнозирования. После того, как будет сформирована корректная модель для обработ­ки временной последовательности, можно разрабатывать соответ­ствующие средства прогнозирования.

Большинство моделей прог­нозирования временных последовательностей разрабатываются для представления этих вариантов последовательностей: константных, тренда, периодических (циклических), или их комбинаций.

Кроме этих моделей существуют их варианты, появляющиеся, когда в процессе, генерирующем переменную, возникают глубинные изменения. Например:

·  на один пе­риод процесс перешел на более высокий уровень, а потом ввернулся на предыдущий уровень;

·  переход на новый уровень остается постоянным;

·  последовательнос­ти, которая некоторое время находилась на постоянном уровне, а потом неожиданно перешла в тренд.

Так как эти три типа изменений достаточно часто встречаются на практике, то необходимо, чтобы прогнозирующая система идентифицировала постоянные изменения и подстраивала модель прогнозирования под изменения в процессе.

Причинные модели используют связь между интересующей временной последовательностью и одной или более другими временны­ми последовательностями. Если эти другие переменные коррелируют с предметной переменной и если существуют причины для этой корреляции, модели прогнозирования, описывающие эти отношения, мо­гут быть очень полезными. В этом случае, зная значение коррели­рующих переменных, можно построить модель прогноза зависимой пе­ременной.

Серьезным ограничением использования причинных моделей яв­ляется требование того, чтобы независимая переменная была извес­тна ко времени, когда делается прогноз.

Другое ограничение причинных методов – большое количество вычис­лений и данных, которое необходимо сравнивать.

Практически, прогнозирующие системы часто используют комби­нацию квантитативных и квалитативных методов. Квантитативные ме­тоды используются для последовательного анализа исторических дан­ных и формирование прогноза. Это придает системе объективность и позволяет эффективно организовать обработку исторических данных. Данные прогноза далее становятся входными данными для субъектив­ной оценки опытными менеджерами, которые могут модифицировать прогноз в соответствии с их взглядами на информацию и их восприя­тие будущего.

На выбор соответствующего метода прогнозирования, влияют следующие факторы:

1)  требуемая форма прогноза;

2)  горизонт, период и интервал прогнозирования;

3)  доступность данных;

4)  требуемая точность;

5)  поведение прогнозируемого процесса;

6)  стоимость разработки, установки и работы с системой;

7)  простота работы с системой;

8)  понимание и сотрудничество управляющих.

Полезным средством при оценке различных методов прогнозирования является симуляция. Метод симуляции основан на ретроспектив­ном использовании исторических данных. Для каждого метода прогно­зирования берется некоторая точка в прошлом и, начиная с нее, вплоть до текущего момента времени проводится симуляция прогнози­рования. Измеренная ошибка прогнозирования может быть использова­на для сравнения методов прогнозирования. Если предполагается, что будущее отличается от прошлого, может быть создана псевдоис­тория, основанная на субъективном взгляде на будущую природу вре­менной последовательности, и использована при симуляции.

3.3  Прогнозирование временных рядов

Фундаментальное предположение о временном ряде

Наблюдаются величины X = X(t), X(t) = (x1(t), x2(t), K, … , xp(t))T, p ≥ 1, и Y = Y(t), Y(t) = (y1(t), y2(t), K, … , yq(t))T, q ≥ 0, в дискретные моменты времени t1 < t2 < K < tk < K.

Обычно рассматривается ситуация, когда наблюдения производятся через равные промежутки времени. В этом случае можно записать: t1 = t0 + 1 ∙ ∆t, t1 = t0 + 2 ∙ ∆t, t1 = t0 + k ∙ ∆t и т. д., где t0 – некоторый начальный момент времени, ∆t – минимальный промежуток времени между наблюдениями.

Задача прогнозирования временного ряда заключается в том, чтобы по его известному участку {ti, X(ti), Y(ti)}Ti =1 оценить будущие значения величины X.

Прежде чем перейти к непосредственному решению данной задачи, необходимо сформулировать ряд фундаментальных предположений о природе временного ряда, в рамках которых можно будет применять ту или иную схему прогнозирования:

·  будущая динамика временного ряда зависит от его предыстории;

·  зависимость временного ряда может со временем меняться, но на некоторых участках она сохраняет определенное постоянство и если меняется, то медленно. Между такими участками могут появляться участки смены закономерности, на которых зависимости сильно изменяются. Глубина предыстории и горизонт прогнозирования также могут меняться во времени по аналогичной схеме;

·  существуют участки временного ряда, на которых действуют одинаковые или близкие зависимости (история повторяется);

·  существуют участки временного ряда, для которых существует принципиальная возможность построения предикторов.

Разложение временного ряда на компоненты

Одно из направлений анализа временных рядов связано с разложением его на компоненты при изучении причин, порождающих изменения. В общем виде временной ряд можно искусственно разложить на следующие составляющие: скачки, тренд, периодические колебания относительно тренда с различной размерностью, случайные помехи и шумы. После исключения из временного ряда скачков, тренда и периодических компонент его можно описать стационарным процессом и применить хорошо развитые квантитативные методы анализа стационарных временных рядов, идея которых состоит в следующем.

Один и тот же предиктор (№1) с разной точностью моделирует разные участки временного ряда. В то же время существует другой предиктор (№2), который на одних участках временного ряда предсказывает лучше, чем предиктор №1, а на других – хуже или так же. Так можно задать целый набор предикторов, которые будут иметь свои особенности. Для прогнозирования выбирается состоящий из последних нескольких значений этого ряда предиктор, который лучше остальных спрогнозирует некоторый участок временного ряда. При правильной настройке системы можно добиться лучшего качества прогнозирования по сравнению с каждым предиктором из заданного набора в отдельности.

Иллюстрация этого подхода представлена на Рис. 2.1.

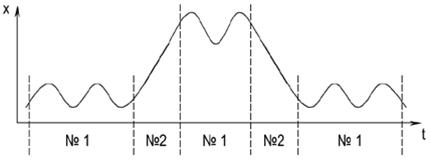
Рис. 2.1 Разложение временного ряда на компоненты

Здесь предиктор №1 имеет вид a1 ∙ sin(a2t + a3) + a4, где a1, K, a4 – настроечные коэффициенты, которые для каждого отдельного участка временного ряда рассчитываются отдельно. Предиктор №2 имеет вид a1t + a2, где a1, a2 – коэффициенты, настраиваемые по аналогичной схеме. Символами «№1» и «№2» обозначены участки временного ряда, на которых предиктор с соответствующим номером имеет лучшие прогнозирующие свойства.

Две основные проблемы, которые необходимо решить при разложении временного ряда на компоненты, заключаются в определении набора предикторов и правила выбора одного из них для прогнозирования некоторого участка временного ряда. Обычно эти проблемы для реальных временных рядов решаются эмпирически.

Предикторы

Ключевым в задаче прогнозирования является понятие «адаптивный предиктор». Предиктором F называется любая вычислительная схема, которая позволяет по значениям одних параметров (входных) получать значения других (выходных).

В качестве выходных задаются те параметры, значения которых нужно спрогнозировать, т. е. в нашем случае это – будущие значения временного ряда. Если, кроме входных параметров, для расчета также используются настроечные коэффициенты, то такой предиктор называют адаптивным. Его применяют тогда, когда имеется некоторый поток данных, к которому нужно постоянно адаптировать работу предиктора. Один из способов, чтобы сделать это, заключается в изменении значений набора настроечных коэффициентов, производимом с помощью некоторой процедуры настройки.

Набор входных и выходных параметров определяет тип предиктора. Если в качестве входных параметров используются значения предыстории временного ряда, то предиктор называется авторегрессионным, например предиктор: 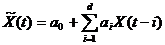где параметр d определяет глубину предыстории или количество элементов временного ряда, используемых для предсказания его будущего значения. Если в качестве аргумента предиктора используется параметр времени t, то предиктор называется трендовым, например: .

Это — наиболее распространенные типы предикторов. Остальные типы предикторов будем относить к категории «другие». Классификация предикторов приведена на Рис. 2.2.

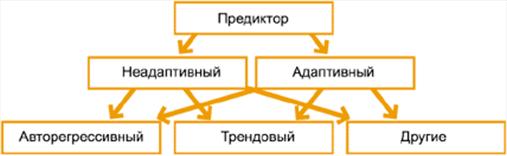
Рис. 2.2 Классификатор предикторов

По определенным признакам все адаптивные предикторы можно объединить в семейства и классы. Семейство представляет некоторую наиболее общую закономерность, например: многочлены, сплайны, нейронные сети, рациональные функции и т. д. Семейство состоит из множества классов, каждый из которых представляет конкретный вид зависимости для данного семейства; при этом каждый класс может рассматриваться в качестве нового семейства, которое также может состоять из классов.

Семейства предикторов, с помощью которых с заданной точностью можно аппроксимировать любую непрерывную функцию, называются семействами универсальных предикторов. К таким семействам можно отнести: многочлены, рациональные функции, сплайны, нейронные сети. Во всех случаях имеет место последовательность вложенных семейств: для многочленов – по степени, для рациональных функций – по максимальной степени числителя и знаменателя, для сплайнов – по числу узлов, для нейронных сетей – по числу нейронов. Данный способ формирования зависимостей может быть положен в основу классификационной схемы семейств адаптивных предикторов.

К семействам адаптивных предикторов, которые могут быть использованы для решения задачи предсказания временного ряда относятся: линейные тренды, квадратичные тренды, тренды k-го порядка, линейные авторегрессионные предикторы, квадратичные авторегрессионные предикторы, авторегрессионные предикторы k-го порядка, нейронные сети и другие адаптивные предикторы. К последней группе принадлежат все предикторы, не вошедшие в перечисленный выше список.

На предиктор могут накладываться ограничения, например, ограничения в виде набора неравенств на значения настроечных коэффициентов предиктора; ограничения на применение процедуры настройки предиктора (настройка допускается только на заданном участке временного ряда, во всех остальных случаях – настроечные коэффициенты не меняются, даже если процедура настройки активирована).

Для прогнозирования будущих значений временного ряда используется процедура прогнозирования. С ней тесно связаны такие понятия, как «глубина прогноза» и «горизонт прогнозирования». Разность времени между моментами начала прогнозирования и его концом будем называть глубиной прогноза. Глубину, при которой прогноз производится с заданной точностью, будем называть горизонтом прогнозирования. Наиболее просто процедура прогнозирования выглядит для трендовых предикторов – в качестве аргумента предиктора нужно указать момент времени, на который требуется получить прогноз, например для момента времени T + 1 прогноз вычисляется следующим образом:

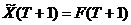(2.1)

При решении задачи прогнозирования временного ряда адаптивным предиктором активно применяется процедура настройки, или обучения [8]. Смысл ее заключается в подборе таких значений настроечных коэффициентов предиктора, которые позволили бы оптимизировать его свойства (заданного критерия). Эта процедура зачастую используется для настройки предиктора на заданную выборку – таблицу, в которой одна часть столбцов описывает значения входных параметров, а другая – значения выходных параметров. Строку такой таблицы называют примером, который обозначают парой (xk, yk), где k – номер примера в выборке 1 ≤ k ≤ N, N – объем выборки, yk – значения выходных параметров, xk – значения входных параметров. Требуется, чтобы предиктор по значениям входных параметров с заданной точностью предсказывал значения выходных параметров для всех примеров выборки. Различают три вида выборок: обучающая, валидационная и тестовая. Первая используется для обучения предиктора, вторая — для выбора его оптимальной архитектуры и/или момента остановки обучения. Наконец, третья, которая вообще не использовалась в обучении, служит для контроля качества прогноза обученного предиктора.

Рассмотрим некоторый адаптивный предиктор: . Настройка этого предиктора F на заданную выборку производится путем подбора настроечных коэффициентов , при этом для определения качества работы предиктора на обучающей выборке будем использовать функцию оценки H, или, просто оценку. В этом случае задача поиска оптимального набора настроечных коэффициентов сводится к оптимизационной задаче: минимизации функции оценки H на обучающей выборке. Перечислим некоторые виды оценок, которые могут быть применены для настройки предикторов:

·  оценка метода наименьших квадратов (МНК) – одна из наиболее простых –определяется как сумма квадратов уклонений от точного решения;

·  оценка МНК с «люфтом» ε. Оценки с люфтом ε, где ε – требуемая точность, позволяют прекращать оптимизацию, если достигнута заданная величина невязок;

·  оценка МНК с весами εi, зависящими от номера выходного сигнала;

·  оценка МНК c люфтом, зависящим от номера выходного сигнала;

·  сумма модулей. Данная оценка определяется как сумма модулей уклонений от точного решения, при этом могут быть рассмотрены аналогичные модификации, как и для метода наименьших квадратов;

·  другие оценки. Возможно использование других норм, представляет также интерес энтропийная оценка.

В процессе настройки требуется оценить работу предиктора на всей выборке. Для этого на основе отдельных оценок формируется оценка всей выборки. Для этого может применяться простое суммирование:

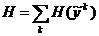(2.2)

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8