. Как провести социологическое исследование (стр. 5 )

Второй способ заключается в “присвоении” каждой анкете соответствующей карточки (их номера должны совпадать). Карточка расчерчивается на квадраты, которые нумеруются в верхнем углу по количеству вопросов в анкете. Затем варианты ответов из анкеты (при позиционной системе кодирования) переносятся на карточку (см. рис. 2).

Рис. 2. Образец карточки для переноса данных из анкеты

Данные с карточек (абсолютное количество ответов по каждому варианту) записываются в таблицы и подсчитывается их процентное соотношение. Наиболее простая – перечневая таблица, составленная на основании ряда распределения по одному признаку (см. табл.2).

Таблица 2

Распределение работников медицинского учреждения по уровню образования (к числу опрошенных)

Таблицы, отображающие ряды распределений по двум и более признакам, называются комбинационными (см. табл. 3).

Наряду с табличными в целях наглядности широко применяется графический способ отображения социологических данных. Наиболее распространенный способ графического представления, обычно используемый для качественных данных – это круговая диаграмма. Каждый сектор круговой диаграммы представляет дискретную категорию переменной. Величина сектора пропорциональна частоте категории для данной выборки. На рис. 3 приведена круговая диаграмма, иллюстрирующая распределение подростков, страдающих вялотекущей формой шизофрении, по возрасту на момент начала заболевания [8].

Таблица 3

Характер актуальности биоэтических проблем в современном обществе

по мнению студентов (n = 255)

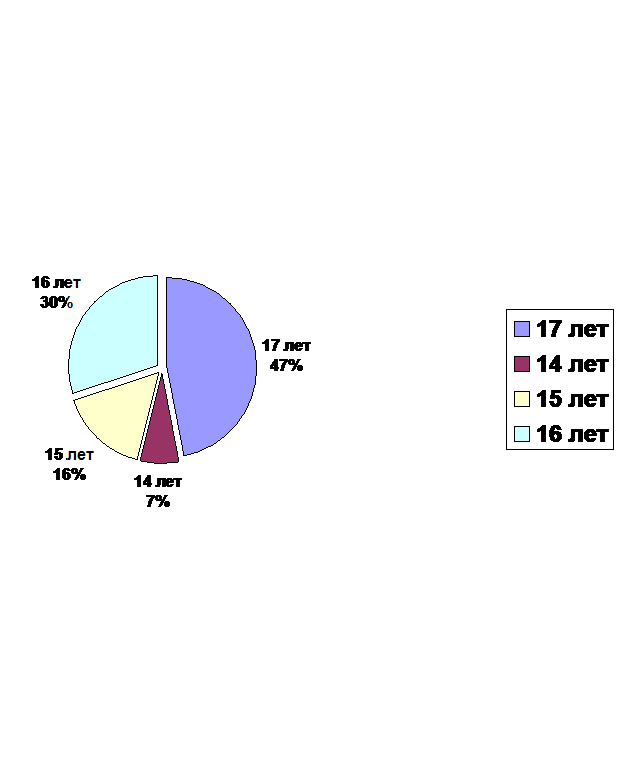
Рис. 3. Заболеваемость вялотекущей формой шизофрении у подростков мужского пола по возрасту, в %.

Кроме круговой диаграммы для отображения эмпирических данных часто используются гистограммы и полигоны. Гистограммы преимущественно используются для отображения непрерывных рядов, а полигон – дискретных. На рис. 4 (см. также табл. 4) показан полигон, изображающий предпочтения жителями г. Челябинска сети аптек (данные исследования, проведенного автором в 2006 г.).

Таблица 4

Предпочтения сети аптек жителями г. Челябинска в 2006 г. (n = 488)

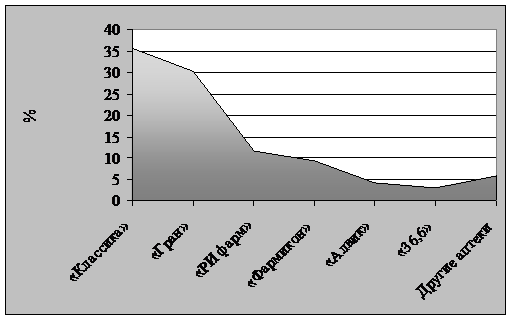
Рис. 4. Предпочтения сети аптек жителями г. Челябинска в 2006 г.

3.2. Аналитические техники и методики обработки, корреляция социологической информации

Какую бы форму представления данных мы не избрали, полученное частотное распределение все еще содержит “слишком много” деталей, не отвечая при этом на весьма важные для содержательного анализа вопросы о самых типичных значениях признака и диапазоне разброса отдельных наблюдений. Для облегчения работы с частотными распределениями, а также для обобщенного представления их характеристик, обычно используют определенные числовые значения – статистики.

Наибольшее практическое значение имеют две группы статистик: меры центральной тенденции и меры изменчивости (разброса).

Меры центральной тенденции указывают на расположение среднего, или типичного значения признака, вокруг которого сгруппированы остальные наблюдения. Понятие среднего, центрального значения в статистике, как и в повседневной жизни, подразумевает нечто “ожидаемое”, “обычное”, “типичное”.

Самый простой из мер центральной тенденции является мода (Мо). Для номинальных переменных мода – единственный способ указать наиболее типичное, распространенное значение. Мода – это такое значение в совокупности наблюдений, которое встречается чаще всего. Например, если в выборке содержится 60% врачей, 30% медсестер и 10% младшего медперсонала, то модальным значением будет “врач”. У моды как меры центральной тенденции есть определенные недостатки, ограничивающие ее интерпретацию. Во-первых, в распределении могут быть две и более моды. Во-вторых, мода чрезвычайно чувствительна к избранному способу группировки значений переменной. Объединяя категории ответа, мы резко увеличиваем число наблюдений в отдельных категориях. Это открывает широкий простор для манипулирования данными. Поэтому “правилом хорошего тона” при вычислении модального значения для сгруппированных количественных данных является выравнивание ширины для всех интервалов класса. Еще одно важное правило касается случаев, когда частоты для всех наблюдаемых значений почти равны. Здесь лучше воздержаться от вычисления моды, так как в этом случае она просто не может быть интерпретирована как мера центральной тенденции. Если, скажем, 48% респондентов поддерживают нововведение, а 49% – нет, то модальное значение определить весьма сложно. И все же во многих случаях вычисление моды необходимо и полезно. Например, для архитектора, занимающегося планированием жилых домов, знание модального значения для размера семьи в данной местности, может оказаться весьма важным.

Другая мера центральной тенденции – медиана (Md) – обычно используется для ординальных переменных, т. е. таких переменных, значение которых могут быть упорядочены от меньших к большим. Медиана – это значение, которое делит упорядоченное множество данных пополам, так что одна половина наблюдений оказывается меньше медианы, а другая – больше. Иными словами, медиана – это 50-й процентиль распределения. При работе с большим массивом данных удобнее всего искать медиану, настроив на основании частотного распределения распределение накопленных частот. Для того чтобы найти медианное значение для маленького массива наблюдений, достаточно упорядочить наблюдения от меньших значений переменной к большим: то значение, которое окажется в середине, и будет медианным. Например, для ряда: 20 баллов, 21 балл, 22 балла, 23 балла, 24 балла, медианой будет 22 балла. Если число значений в группе наблюдений четное, то медианой будет среднее двух центральных значений. Медиана может совпадать или не совпадать с модой. При этом медиана лучше всего соответствует нашему интуитивному представлению о середине упорядоченной последовательности чисел. Некоторые исследователи даже полагают, что медиана – лучше и “справедливее” среднеарифметического при описании таких величин, как, скажем доход семьи. Ведь семьи, имеющие доход ниже среднего, могут составить и 60% и 70% населения. Когда же мы говорим, например, что медианный доход составил 50 тыс. рублей в год, то не более 50% семей окажутся “ниже среднего уровня”. На медиану не влияют величины “крайних” очень больших или малых значений.

И все же для количественных переменных самой важной и распространенной является другая мера центральной тенденции – среднее арифметическое, которое чаще всего называют просто средним (и обозначают как Хср.). Процедура определения среднего общеизвестна: нужно просуммировать все значения наблюдений и разделить полученную сумму на число наблюдений. В общем случае:

Хср. = Х1 + Х2 + …+ Хn

n

где Х1…Хn – наблюдаемые значения; n – число наблюдений.

Среднее обладает рядом важных свойств. В частности, если сложить все значения отклонений от среднего значения, т. е. разности между Хср. и Х1, Х2, ….Хn (которые могут быть и положительными и отрицательными), то сумма отклонений будет равна нулю. Кроме того, сумма квадратов отклонений наблюдаемых значений от их арифметического среднего меньше суммы квадратов отклонений от любой другой точки. Эти свойства среднего определять его уникальную роль в решении ряда статических задач, о которых мы будем говорить ниже. Сейчас достаточно отметить то обстоятельство, что при использовании среднего в качестве “представителя” (т. е. статической оценки) каждого из наблюдаемых значений, ошибка, определяемая как сумма квадратов отклонений, будет минимальный. Не стоит, однако, забывать о том, что минимальная ошибка может быть достаточно большой. Так, для малых выборок, имеющих более чем одну моду, любая мера центральной тенденции, включая среднее, будет недостаточно хороша. Центральной тенденции в таком распределении просто не существует.

Сравнение значений средних показателей для различных выборок или одной и той же выборки в разные моменты времени – весьма распространенный способ анализа результатов. Следует, однако, помнить о том, что заведомо некорректны сравнения различных мер центральной тенденции, например, медианы и среднего. Причина здесь в том, что различные меры описывают разные характеристики распределения: медиана – среднее положение, мода – самое часто встречающееся значение и т. д. Кроме того, даже две одинаковые меры центральной тенденции не всегда сравнимы. Средние двух распределений имеет смысл сравнивать лишь в том случае, если во всех других отношениях распределения одинаковые и имеют сходную форму.

Очевидно, важно еще также не только знать, что типично для выборки наблюдений, но и установить, насколько выражены отклонения от типичных значений. Чтобы определить, насколько хорошо та или иная мера центральной тенденции описывает распределение, нужно воспользоваться какой-либо мерой изменчивости, разброса.

Самая грубая мера изменчивости – размах (диапазон) значений. Эта мера не учитывает индивидуальные отклонения значений, описывая лишь диапазон их изменчивости. Под размахом понимают разность между максимальным и минимальным наблюдаемым значением. Если количество денег, затраченных в месяц на лекарства в группе из десяти человек варьирует от 50 руб. (1 человек) до 1000 руб. (2 человека), размах будет равен 1000 – 50 = 950.

Еще одна грубая мера разброса значений – это коэффициент вариации (V), который определяется просто как процент наблюдений, лежащих вне модального интервала, т. е. процент (доля) наблюдений, не совпадающих с модальным значением. Если от модального отличаются 70% значений, то V = 70% (или V = 0,7).

Очень удобный показатель разброса значений для ординальной переменной – междуквартильный размах, связанный со шкалой равнокажущихся интервалов Л. Терстоуна. Шкала Терстоуна позволяет расположить и суждения и индивидов вдоль одномерного континуума установки, полюсам которого соответствует крайне благожелательное и крайне негативное отношение к объекту установки (платной медицине, прогрессивному налогообложению или чему-либо еще). Шкальный балл суждения или индивида отражает степень этой благожелательности или неблагожелательности. Полумеждуквартильный размах равен половине расстояния между третьим и первым квартилями:

Q = Q3 - Q1

2

Нижний, первый квартиль (Q1) отсекает 25% наблюдений, а ниже третьего квартиля (Q3) лежат уже 75% случаев. Если распределение приблизительно симметрично, то можно считать, что полумеждуквартильный размах указывает границы, в которых лежит 50% данных по обе стороне медианы или среднего.

Все эти меры изменчивости можно считать скорее грубыми и приблизительными. Ни одна из них не уделяет должного внимания информации об отношениях каждого отдельного наблюдаемого значения от среднего, хотя эта информация в большинства случаев может быть получена из анализа распределения. Информацию о вариации некоторой совокупности значений относительно среднего несут значения отклонений от среднего, о некоторых мы уже говорили. Однако, просуммировав все значения отклонений (Хср – Хi), мы получим нуль.

Положительные и отрицательные отклонения будут взаимоуничтожаться. Если же мы возведем в квадрат каждое отклонение и просуммируем квадраты отклонений, то мы получим хорошую меру рассеяния, которая будет маленькой, когда данные однородны, и большой, когда данные неоднородны. Чтобы суммы квадратов отклонений для выборок разного размера можно было сравнивать, нужно поделить каждую из них на N, где N – объем выборки. Для небольших выборок (N < 100) лучше делить на (N – 1).

Именно так и получают важнейшую меру рассеяния – дисперсию (S2). Если Хср. – среднее, Х1, Х2…Хn – индивидуальные значения измеряемой переменной Х в данной совокупности, а N – объем выборки:

S (Хi – Xср.)2

S2 = N

Для того чтобы вычислить значение дисперсии, нужно вычесть из каждого наблюдаемого значения среднее, возвести в квадрат все полученные отклонения, сложить квадраты отклонений и разделить полученную сумму на объем выборки. Величина, равная квадратному корню из дисперсии, называется стандартным отклонением (Sx), т. е.:

Sx = ÖS2

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8 9